西师大版六年级数学上册 2.5 圆的面积(1) 课件(20张ppt)
文档属性
| 名称 | 西师大版六年级数学上册 2.5 圆的面积(1) 课件(20张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 西师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-06 09:35:32 | ||
图片预览





文档简介
西师版数学六年级(上)
第5课时 圆的面积(1)
圆
二
1.理解圆的面积计算公式的推导过程,掌握圆的面积
的计算方法,并能进行简单的计算 。
2. 经历圆的面积公式的推导过程,培养学生观察、分
析、归纳、概括的思维能力。
3.通过探究、合作、交流等学习活动,激发学生的学
习兴趣,增强学好数学的信心 。
学习目标
【重点】
圆的面积的计算公式。
【难点】
圆的面积计算公式的推导。
课堂导入
回忆一下,平行四边形的面积公式是怎样推导出来的?
原来平行四边形的底
原来平行四边形的高
(长方形的长)
(长方形的宽)
云南景洪的曼飞龙白塔的塔基为圆柱形石座,底面周长是42.6米。
这座塔的塔基占地多少平方米?
求塔基的面积就是求圆的面积
新知探究
正方形的面积=边长×边长。
1
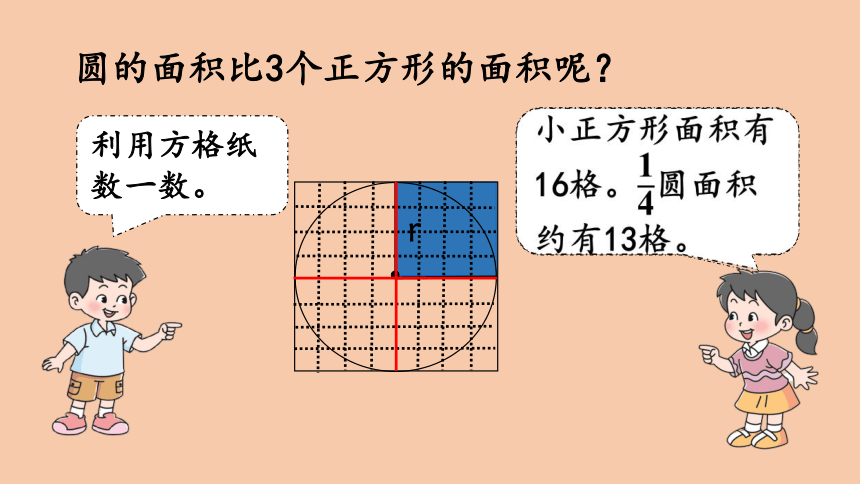
探索圆的面积与半径有什么关系?
画一个边长为r的正方形,再以正方形的边长为半径画一个圆。
·
r
圆的面积比2个正方形的面积大,比4个正方形的面积小。
·
r
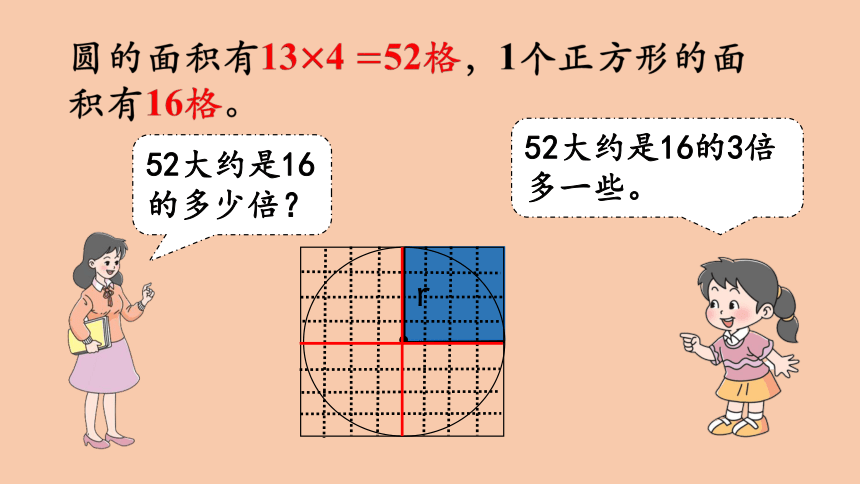
圆的面积比3个正方形的面积呢?
·
r
利用方格纸数一数。
?
?
·
r
52大约是16的多少倍?
52大约是16的3倍多一些。
1
2
3
4
5
6
7
8
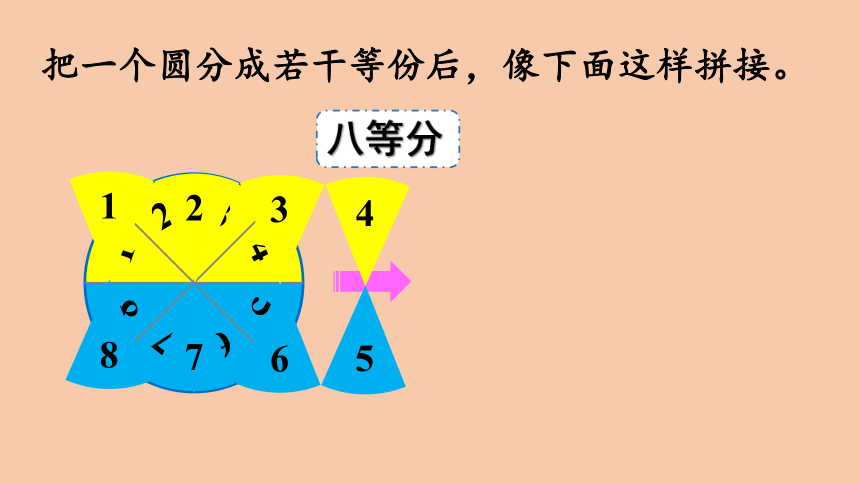
八等分
2
1
4
3
7
8
5
6
把一个圆分成若干等份后,像下面这样拼接。
十六等分
1
2
3
4
5
6
7
8
16
15
14
13
12
11
10
9
1
2
3
4
5
6
7
8
16
15
14
13
12
11
10
9
三十二等分
以拼成的近似平行四边形为例:
圆8等分时:
圆16等分时:
圆32等分时:
2
1
4
3
7
8
5
6
1
2
3
4
5
6
7
8
16
15
14
13
12
11
10
9
平均分的份数越多,拼成的图形越接近长方形。
C
2
r
从上图中可以看出圆的半径是r,长方形的宽近似( ),长近似于( )。
圆周长的一半
圆的半径
因为: 长方形面积= 长 × 宽
所以: 圆的面积 = ×
πr
r
C=2πr
πr?
=
如果用S表示圆的面积,那么圆的面积计算公式就是 :
S=πr?
课堂练习
教材第21页“练习五”第1题
1.公园草地上的自动旋转喷水器的射程是8m。它能喷洒的面积是多少平方米?
?
?
?
(平方米)
答:它能喷洒的面积是200.96平方米。
提示:喷水器的射程是圆的半径,根据圆的面积公式计算
2.一个圆形水缸口的外直径为1m。现在为这个水缸做一个盖子,这个盖子的面积至少是多少平方米?
?
?
?
?
(平方米)
答:这个盖子的面积至少是0.785平方米。
提示:已知盖子的直径,先算半径,再根据圆的面积公式计算。
?
教材第21页“练习五”第2题
3.填空。
教材第21页“练习五”第3题
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}半径(cm)
直径(cm)
周长(cm)
10
4
56.52
5
31.4
78.5
8
50.24
25.12
9
18
254.34
?
4.用下面这张长方形剪出一个最大圆。
14cm
20cm
圆的直径是多少?
圆的面积是多少?
教材第21页“练习五”第4题
由图可知,这个圆的直径等于长方形的宽,所以半径等于长方形的宽的一半。
?
?
?
?
(平方厘米)
(厘米)
答:圆的直径是7厘米,圆的面积是153.86平方厘米。
?
半径是直径的一半。
同学们,这节课你有什么收获?
课堂小结
1、把圆沿半径剪拼成一个长方形,长方形的长近似等于圆周长的一半(πr),宽近似等于圆的半径(r)。
2、圆的面积计算公式:S=πr?。
3、已知直径或周长求面积时,可以先计算半径的长度,再求面积。
02
01
课后作业
课后练习第4、5题。
作业课件中的相关练习。
第5课时 圆的面积(1)
圆
二
1.理解圆的面积计算公式的推导过程,掌握圆的面积
的计算方法,并能进行简单的计算 。
2. 经历圆的面积公式的推导过程,培养学生观察、分
析、归纳、概括的思维能力。
3.通过探究、合作、交流等学习活动,激发学生的学
习兴趣,增强学好数学的信心 。
学习目标
【重点】
圆的面积的计算公式。
【难点】
圆的面积计算公式的推导。
课堂导入
回忆一下,平行四边形的面积公式是怎样推导出来的?
原来平行四边形的底
原来平行四边形的高
(长方形的长)
(长方形的宽)
云南景洪的曼飞龙白塔的塔基为圆柱形石座,底面周长是42.6米。
这座塔的塔基占地多少平方米?
求塔基的面积就是求圆的面积
新知探究
正方形的面积=边长×边长。
1
探索圆的面积与半径有什么关系?
画一个边长为r的正方形,再以正方形的边长为半径画一个圆。
·
r
圆的面积比2个正方形的面积大,比4个正方形的面积小。
·
r
圆的面积比3个正方形的面积呢?
·
r
利用方格纸数一数。
?
?
·
r
52大约是16的多少倍?
52大约是16的3倍多一些。
1
2
3
4
5
6
7
8
八等分
2
1
4
3
7
8
5
6
把一个圆分成若干等份后,像下面这样拼接。
十六等分
1
2
3
4
5
6
7
8
16
15
14
13
12
11
10
9
1
2
3
4
5
6
7
8
16
15
14
13
12
11
10
9
三十二等分
以拼成的近似平行四边形为例:
圆8等分时:
圆16等分时:
圆32等分时:
2
1
4
3
7
8
5
6
1
2
3
4
5
6
7
8
16
15
14
13
12
11
10
9
平均分的份数越多,拼成的图形越接近长方形。
C
2
r
从上图中可以看出圆的半径是r,长方形的宽近似( ),长近似于( )。
圆周长的一半
圆的半径
因为: 长方形面积= 长 × 宽
所以: 圆的面积 = ×
πr
r
C=2πr
πr?
=
如果用S表示圆的面积,那么圆的面积计算公式就是 :
S=πr?
课堂练习
教材第21页“练习五”第1题
1.公园草地上的自动旋转喷水器的射程是8m。它能喷洒的面积是多少平方米?
?
?
?
(平方米)
答:它能喷洒的面积是200.96平方米。
提示:喷水器的射程是圆的半径,根据圆的面积公式计算
2.一个圆形水缸口的外直径为1m。现在为这个水缸做一个盖子,这个盖子的面积至少是多少平方米?
?
?
?
?
(平方米)
答:这个盖子的面积至少是0.785平方米。
提示:已知盖子的直径,先算半径,再根据圆的面积公式计算。
?
教材第21页“练习五”第2题
3.填空。
教材第21页“练习五”第3题
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}半径(cm)
直径(cm)
周长(cm)
10
4
56.52
5
31.4
78.5
8
50.24
25.12
9
18
254.34
?
4.用下面这张长方形剪出一个最大圆。
14cm
20cm
圆的直径是多少?
圆的面积是多少?
教材第21页“练习五”第4题
由图可知,这个圆的直径等于长方形的宽,所以半径等于长方形的宽的一半。
?
?
?
?
(平方厘米)
(厘米)
答:圆的直径是7厘米,圆的面积是153.86平方厘米。
?
半径是直径的一半。
同学们,这节课你有什么收获?
课堂小结
1、把圆沿半径剪拼成一个长方形,长方形的长近似等于圆周长的一半(πr),宽近似等于圆的半径(r)。
2、圆的面积计算公式:S=πr?。
3、已知直径或周长求面积时,可以先计算半径的长度,再求面积。
02
01
课后作业
课后练习第4、5题。
作业课件中的相关练习。
