1.1生活中的立体图形第二课时同步练习2021-2022学年北师大版七年级上册(Word版含答案)
文档属性
| 名称 | 1.1生活中的立体图形第二课时同步练习2021-2022学年北师大版七年级上册(Word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 127.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-06 10:45:29 | ||
图片预览


文档简介
第一章
丰富的图形世界
第1节
生活中的立体图形(第二课时)
一.选择题
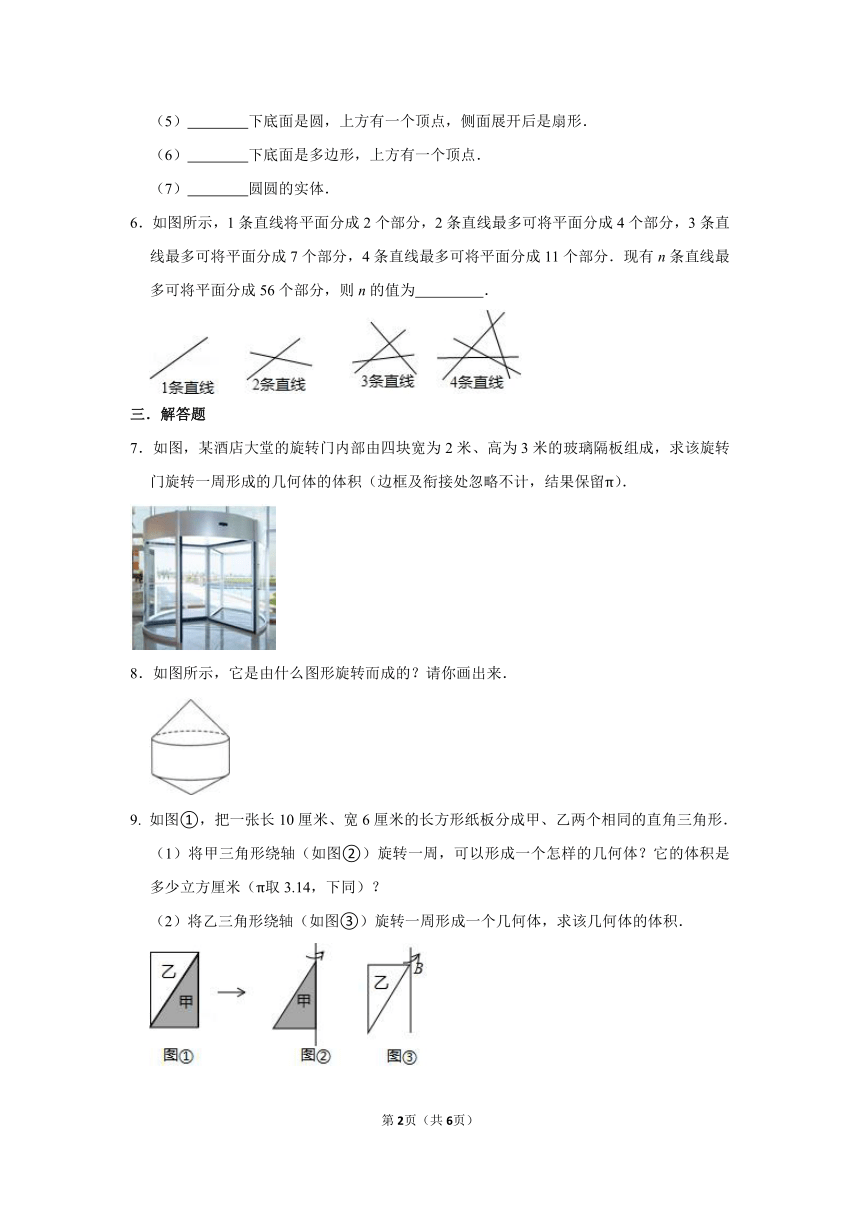
1.观察下图,把左边的图形绕着给定的直线旋转一周后可能形成的立体图形是( )
A.
B.
C.
D.
2.如图:CD是直角三角形ABC的高,将直角三角形ABC按以下方式旋转一周可以得到右侧几何体的是( )
A.绕着AC旋转
B.绕着AB旋转
C.绕着CD旋转
D.绕着BC旋转
3.一个直角三角形的三条边分别为3、4、5,将这个三角形绕它的直角边所在直线旋转一周得到的几何体的体积是( )
A.12π
B.16π
C.12π或16π
D.36π或48π
二.填空题
4.如图,用棱长为a的小正方体拼成长方体,按照这样的拼法,第n个长方体表面积是
.
5.
根据几何体的特征,填写它们的名称.
(1)
上下两个底面是大小相同的圆,侧面展开后是长方形.
(2)
6个面都是长方形.
(3)
6个面都是正方形.
(4)
上下底面是形状大小相同的多边形,侧面是长方形.
(5)
下底面是圆,上方有一个顶点,侧面展开后是扇形.
(6)
下底面是多边形,上方有一个顶点.
(7)
圆圆的实体.
6.如图所示,1条直线将平面分成2个部分,2条直线最多可将平面分成4个部分,3条直线最多可将平面分成7个部分,4条直线最多可将平面分成11个部分.现有n条直线最多可将平面分成56个部分,则n的值为
.
三.解答题
7.如图,某酒店大堂的旋转门内部由四块宽为2米、高为3米的玻璃隔板组成,求该旋转门旋转一周形成的几何体的体积(边框及衔接处忽略不计,结果保留π).
8.如图所示,它是由什么图形旋转而成的?请你画出来.
9.
如图①,把一张长10厘米、宽6厘米的长方形纸板分成甲、乙两个相同的直角三角形.
(1)将甲三角形绕轴(如图②)旋转一周,可以形成一个怎样的几何体?它的体积是多少立方厘米(π取3.14,下同)?
(2)将乙三角形绕轴(如图③)旋转一周形成一个几何体,求该几何体的体积.
10.
如图所示是我们在运动场上踢的足球,而大多的足球是由许多小黑白块的皮缝合而成的.小强和小刚两位同学,一天在玩足球时研究起足球上的黑白块的个数,结果发现黑块都是五边形,白块都是六边形.小强好不容易才数清了黑块共12块,小刚数白块时不是重复,就是遗漏,无法数清白块的个数,你能帮助小刚解决这一问题吗?
11.
如图是一个长方体储水箱和一个长方体水池的侧面示意图(厚度忽略不计),储水箱中水深12dm,把一高度为14dm的长方体石柱放置于水池中央后水池中水深2dm.现将储水箱中的水匀速注入水池.注水4min时水池水面与石柱上底面持平;继续注水2min后,储水箱中的水全部注入水池,此时水池中水深19dm.根据上述信息,解答下列问题:
(1)注水多长时间时,储水箱和水池中的水的深度相同?
(2)若水池底面积为42dm2,求石柱的底面积;
(3)若石柱的体积为168dm3,请直接写出注水前储水箱中水的体积.
第1节
生活中的立体图形(第二课时)答案解析
一.选择题
1.D
【解析】解:由图形可以看出,左边的长方形的竖直的两个边与已知的直线平行,因而这两条边旋转形成两个柱形表面,因而旋转一周后可能形成的立体图形是一个管状的物体.故选:D.
2.B
【解析】解:将直角三角形ABC绕斜边AB所在直线旋转一周得到的几何体是,
故选:B.
3.C
【解析】解:∵个直角三角形的三条边分别为3、4、5,
且直角三角形的斜边大于直角边,
∴两直角边为3,4.
①以直角边为3所在直线旋转一周得到一个圆锥,底面半径是4,高是3,
所以V==,
②以直角边为4所在直线旋转一周得到一个圆锥,底面半径是3,高是4,
所以V==π?32?4=12π,
故选:C.
二.填空题
4.(4n+6)a2
【解析】解:根据题干分析可得:第n个长方体的表面积是:4n+6个小正方体的面;
小正方体的一个面的面积为:a×a=a2,
所以第n个长方体的表面积为:[(n+1)×4+2]a2=(4n+6)a2.
故答案为:(4n+6)a2.
5.
圆柱;长方体;正方体;棱柱;圆锥;棱锥;球.
【解析】解:由几何体的特征可知,几何体的名称依次为:
(1)圆柱;(2)长方体;(3)正方体;(4)棱柱;(5)圆锥;(6)棱锥;(7)球.
故答案为:圆柱;长方体;正方体;棱柱;圆锥;棱锥;球.
6.10
【解析】解:依题意有
n(n+1)+1=56,
解得n1=﹣11(不合题意舍去),n2=10.
答:n的值为10.
故答案为:10.
三.解答题
7.体积是12πm3.
【解析】解:该旋转门旋转一周形成的几何体是圆柱,体积为:
π×22×3=12π(m3).
故形成的几何体的体积是12πm3.
8.【解析】解:面动成体,直角三角形绕直角边旋转一周可得圆锥,长方形绕一边旋转一周可得圆柱,那么所求的图形是直角三角形,长方形,直角三角形的组合图形.
9.
【解析】解:(1)根据题干分析可得:以其中一个直角三角形较长的直角边所在直线为轴,将纸板快速转动,可以形成一个圆锥,
它的体积是×3.14×62×10,
=3.14×12×10,
=376.8(立方厘米);
(2)根据题干分析可得:乙三角形(如图③)旋转一周,可以形成一个空心的圆柱.
体积为:3.14×62×10﹣×3.14×62×10
=3.14×360﹣3.14×120
=3.14×240
=753.6(立方厘米).
10.
【解析】解:设白块有x块,则:3x=5×12,
解得:x=20.
答:白块有20块.
【解析】(1)储水箱出水速度:12÷6=2(dm/min),
水池注水速度:(14﹣2)÷4=3(dm/min),
设tmin时深度相同,则:
12﹣2t=2+3t,
解得:t=2,
答:注水2min时,储水箱和水池中的水的深度相同.
(2)设石柱底面积S=adm2,
则:(14﹣2)×(42﹣a)=2×(19﹣14)×42,
解得:a=7,
故石柱的底面积为7dm2.
(3)∵石柱的体积为168dm3,
∴石柱的底面积为:168÷14=12(dm2),
依题意,得:
(19﹣14)?S水池÷(6﹣4)=(14﹣2)?(S水池﹣12)÷4,
解得:S水池=72(dm2),
12÷6×4×S储水箱=(72﹣12)×(14﹣2),
解得:S储水箱=90(dm2),
∴注水前储水箱中水的体积V=S储水箱?h=90×12=1080(dm3).
第10页(共10页)
丰富的图形世界
第1节
生活中的立体图形(第二课时)
一.选择题
1.观察下图,把左边的图形绕着给定的直线旋转一周后可能形成的立体图形是( )
A.
B.
C.
D.
2.如图:CD是直角三角形ABC的高,将直角三角形ABC按以下方式旋转一周可以得到右侧几何体的是( )
A.绕着AC旋转
B.绕着AB旋转
C.绕着CD旋转
D.绕着BC旋转
3.一个直角三角形的三条边分别为3、4、5,将这个三角形绕它的直角边所在直线旋转一周得到的几何体的体积是( )
A.12π
B.16π
C.12π或16π
D.36π或48π
二.填空题
4.如图,用棱长为a的小正方体拼成长方体,按照这样的拼法,第n个长方体表面积是
.
5.
根据几何体的特征,填写它们的名称.
(1)
上下两个底面是大小相同的圆,侧面展开后是长方形.
(2)
6个面都是长方形.
(3)
6个面都是正方形.
(4)
上下底面是形状大小相同的多边形,侧面是长方形.
(5)
下底面是圆,上方有一个顶点,侧面展开后是扇形.
(6)
下底面是多边形,上方有一个顶点.
(7)
圆圆的实体.
6.如图所示,1条直线将平面分成2个部分,2条直线最多可将平面分成4个部分,3条直线最多可将平面分成7个部分,4条直线最多可将平面分成11个部分.现有n条直线最多可将平面分成56个部分,则n的值为
.
三.解答题
7.如图,某酒店大堂的旋转门内部由四块宽为2米、高为3米的玻璃隔板组成,求该旋转门旋转一周形成的几何体的体积(边框及衔接处忽略不计,结果保留π).
8.如图所示,它是由什么图形旋转而成的?请你画出来.
9.
如图①,把一张长10厘米、宽6厘米的长方形纸板分成甲、乙两个相同的直角三角形.
(1)将甲三角形绕轴(如图②)旋转一周,可以形成一个怎样的几何体?它的体积是多少立方厘米(π取3.14,下同)?
(2)将乙三角形绕轴(如图③)旋转一周形成一个几何体,求该几何体的体积.
10.
如图所示是我们在运动场上踢的足球,而大多的足球是由许多小黑白块的皮缝合而成的.小强和小刚两位同学,一天在玩足球时研究起足球上的黑白块的个数,结果发现黑块都是五边形,白块都是六边形.小强好不容易才数清了黑块共12块,小刚数白块时不是重复,就是遗漏,无法数清白块的个数,你能帮助小刚解决这一问题吗?
11.
如图是一个长方体储水箱和一个长方体水池的侧面示意图(厚度忽略不计),储水箱中水深12dm,把一高度为14dm的长方体石柱放置于水池中央后水池中水深2dm.现将储水箱中的水匀速注入水池.注水4min时水池水面与石柱上底面持平;继续注水2min后,储水箱中的水全部注入水池,此时水池中水深19dm.根据上述信息,解答下列问题:
(1)注水多长时间时,储水箱和水池中的水的深度相同?
(2)若水池底面积为42dm2,求石柱的底面积;
(3)若石柱的体积为168dm3,请直接写出注水前储水箱中水的体积.
第1节
生活中的立体图形(第二课时)答案解析
一.选择题
1.D
【解析】解:由图形可以看出,左边的长方形的竖直的两个边与已知的直线平行,因而这两条边旋转形成两个柱形表面,因而旋转一周后可能形成的立体图形是一个管状的物体.故选:D.
2.B
【解析】解:将直角三角形ABC绕斜边AB所在直线旋转一周得到的几何体是,
故选:B.
3.C
【解析】解:∵个直角三角形的三条边分别为3、4、5,
且直角三角形的斜边大于直角边,
∴两直角边为3,4.
①以直角边为3所在直线旋转一周得到一个圆锥,底面半径是4,高是3,
所以V==,
②以直角边为4所在直线旋转一周得到一个圆锥,底面半径是3,高是4,
所以V==π?32?4=12π,
故选:C.
二.填空题
4.(4n+6)a2
【解析】解:根据题干分析可得:第n个长方体的表面积是:4n+6个小正方体的面;
小正方体的一个面的面积为:a×a=a2,
所以第n个长方体的表面积为:[(n+1)×4+2]a2=(4n+6)a2.
故答案为:(4n+6)a2.
5.
圆柱;长方体;正方体;棱柱;圆锥;棱锥;球.
【解析】解:由几何体的特征可知,几何体的名称依次为:
(1)圆柱;(2)长方体;(3)正方体;(4)棱柱;(5)圆锥;(6)棱锥;(7)球.
故答案为:圆柱;长方体;正方体;棱柱;圆锥;棱锥;球.
6.10
【解析】解:依题意有
n(n+1)+1=56,
解得n1=﹣11(不合题意舍去),n2=10.
答:n的值为10.
故答案为:10.
三.解答题
7.体积是12πm3.
【解析】解:该旋转门旋转一周形成的几何体是圆柱,体积为:
π×22×3=12π(m3).
故形成的几何体的体积是12πm3.
8.【解析】解:面动成体,直角三角形绕直角边旋转一周可得圆锥,长方形绕一边旋转一周可得圆柱,那么所求的图形是直角三角形,长方形,直角三角形的组合图形.
9.
【解析】解:(1)根据题干分析可得:以其中一个直角三角形较长的直角边所在直线为轴,将纸板快速转动,可以形成一个圆锥,
它的体积是×3.14×62×10,
=3.14×12×10,
=376.8(立方厘米);
(2)根据题干分析可得:乙三角形(如图③)旋转一周,可以形成一个空心的圆柱.
体积为:3.14×62×10﹣×3.14×62×10
=3.14×360﹣3.14×120
=3.14×240
=753.6(立方厘米).
10.
【解析】解:设白块有x块,则:3x=5×12,
解得:x=20.
答:白块有20块.
【解析】(1)储水箱出水速度:12÷6=2(dm/min),
水池注水速度:(14﹣2)÷4=3(dm/min),
设tmin时深度相同,则:
12﹣2t=2+3t,
解得:t=2,
答:注水2min时,储水箱和水池中的水的深度相同.
(2)设石柱底面积S=adm2,
则:(14﹣2)×(42﹣a)=2×(19﹣14)×42,
解得:a=7,
故石柱的底面积为7dm2.
(3)∵石柱的体积为168dm3,
∴石柱的底面积为:168÷14=12(dm2),
依题意,得:
(19﹣14)?S水池÷(6﹣4)=(14﹣2)?(S水池﹣12)÷4,
解得:S水池=72(dm2),
12÷6×4×S储水箱=(72﹣12)×(14﹣2),
解得:S储水箱=90(dm2),
∴注水前储水箱中水的体积V=S储水箱?h=90×12=1080(dm3).
第10页(共10页)
同课章节目录
- 第一章 丰富的图形世界
- 1.1 生活中的立体图形
- 1.2 展开与折叠
- 1.3 截一个几何体
- 1.4 从三个不同方向看物体的形状
- 第二章 有理数及其运算
- 2.1 有理数
- 2.2 数轴
- 2.3 绝对值
- 2.4 有理数的加法
- 2.5 有理数的减法
- 2.6 有理数的加减混合运算
- 2.7 有理数的乘法
- 2.8 有理数的除法
- 2.9 有理数的乘方
- 2.10 科学记数法
- 2.11 有理数的混合运算
- 2.12 用计算器进行运算
- 第三章 整式及其加减
- 3.1 字母表示数
- 3.2 代数式
- 3.3 整式
- 3.4 整式的加减
- 3.5 探索与表达规律
- 第四章 基本平面图形
- 4.1 线段、射线、直线
- 4.2 比较线段的长短
- 4.3 角
- 4.4 角的比较
- 4.5 多边形和圆的初步认识
- 第五章 一元一次方程
- 5.1 认识一元一次方程
- 5.2 求解一元一次方程
- 5.3 应用一元一次方程——水箱变高了
- 5.4 应用一元一次方程——打折销售
- 5.5 应用一元一次方程——“希望工程”义演
- 5.6 应用一元一次方程——追赶小明
- 第六章 数据的收集与整理
- 6.1 数据的收集
- 6.2 普查和抽样调查
- 6.3 数据的表示
- 6.4 统计图的选择
