19.1.2平行四边形的判定(2)
文档属性
| 名称 | 19.1.2平行四边形的判定(2) |  | |
| 格式 | zip | ||
| 文件大小 | 443.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-04-23 22:01:23 | ||
图片预览




文档简介
(共17张PPT)
聪明出于勤奋,天才在于积累。
-华罗庚
八年级数学备课组 邹 茜
1、掌握用“一组对边平行且相等”来判定平行四边形的方法;
2、能根据平行四边形的判别方法进行有关的证明。
一天八年级的李明同学在生物实验室做实验时,不小心碰碎了实验室的一块平行四边形的实验用的玻璃片,只剩下如图所示部分,他想去割一块赔给学校,带上玻璃剩下部分去玻璃店不安全,于是他想把原来的平行四边形重新在纸上画出来,然后带上图纸去就行了,可原来的平行四边形怎么画出来呢?(提示:A,B,C为三顶点,找出第四个顶点D即可)
A
B
C
想一想
D
A
B
C
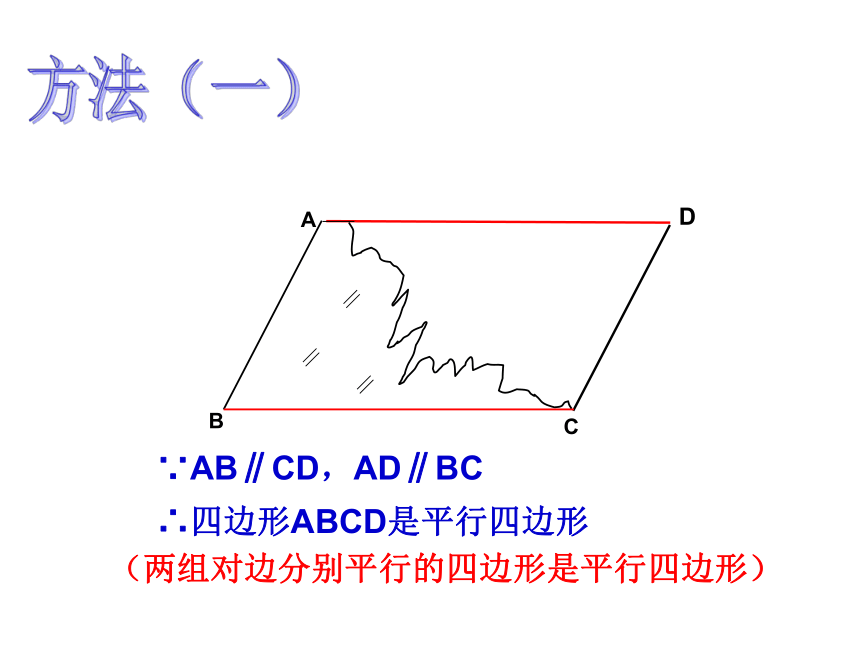
(两组对边分别平行的四边形是平行四边形)
∵AB∥CD,AD∥BC
∴四边形ABCD是平行四边形
D
A
B
C
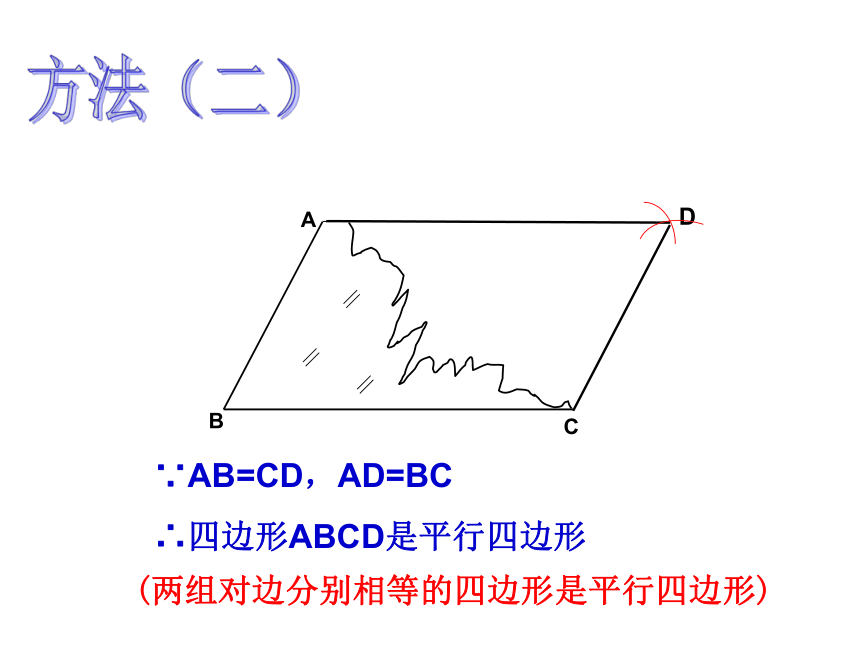
(两组对边分别相等的四边形是平行四边形)
∵AB=CD,AD=BC
∴四边形ABCD是平行四边形
D
O
A
B
C
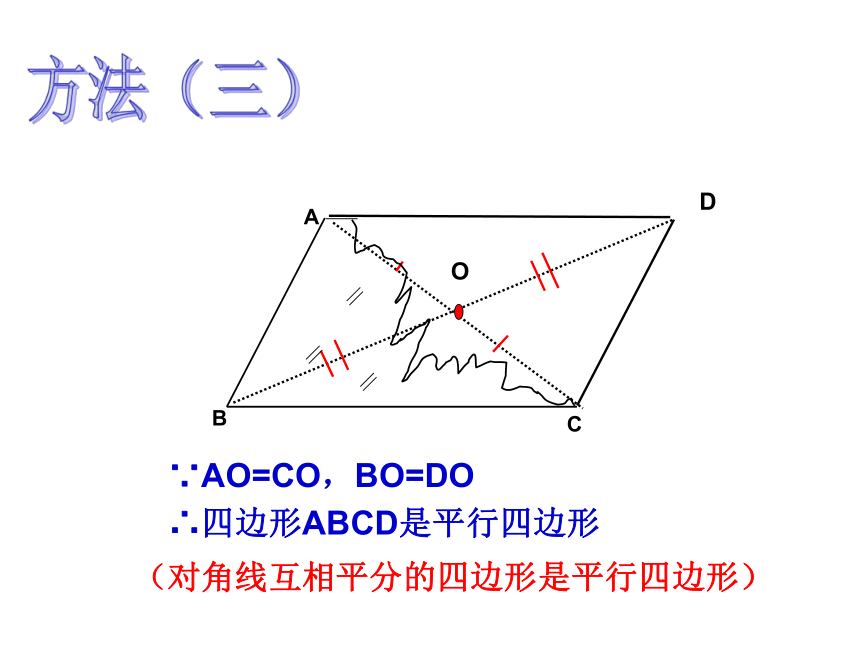
(对角线互相平分的四边形是平行四边形)
∵AO=CO,BO=DO
∴四边形ABCD是平行四边形
D
A
B
C
A
B
C
D
一组对边平行且相等的四边形是平行四边形?
∵AB CD, ∴四边形ABCD是平行四边形
∥
﹦
猜想,对吗?
A
B
C
D
求证:四边形ABCD是平行四边形。
证明:连接AC
∵AD∥BC
∴∠DAC=∠ACB
又∵AD=BC,AC=AC,
∴ΔABC≌ΔCDA
∴∠BAC=∠ACD
∴AB∥CD
∴四边形ABCD是平行四边形
已知:在四边形ABCD中, AD BC。
(两组对边分别平行的四边形是平行四边形)
你还有其他证法吗?
一组对边平行且相等的四边形是平行四边形
平行四边形的判定定理4:
符号语言:
∵AB CD
∴四边形ABCD是平行四边形
(一组对边平行且相等的四边形是平行四边形)
A
B
C
D
从边判定
1、两组对边分别平行的四边形是平行四边形
2、两组对边分别相等的四边形是平行四边形
3、一组对边平行且相等的四边形是平行四边形
从角判定
两组对角分别相等的四边形是平行四边形
从对角线判定
两条对角线互相平分的四边形是平行四边形
理一理
平行四边形的判定方法
1、已知在四边形ABCD中,AD∥BC,要使这个四边形为平行四边形,则需添加一个你认为正确的条件为 ( )
A B∥DC,或∠A =∠C或AD=BC
2、能判定一个四边形是平行四边形的条件是( )
A、一组对角相等 B、一组对边平行且相等
C、一对邻角互补 D、两条对角线互相垂直
B
3、四边形ABCD中,若∠A = ∠C,∠B = ∠D,则下列结论中错误的是( )
C
A、AB = CD B、AD∥BC
C、∠A = ∠B D、对角线互相平分
4、如图,在 ABCD的一组对边AD、BC上截取EF=MN,连接EM、FN,那么EM和FN有怎样的关系?为什么?
A
B
C
D
E
F
M
N
5、已知:如图,E、F分别是 ABCD 的边AD,BC的中点。
求证:BE=DF.
D
F
E
C
B
A
证明:
∵四边形ABCD是平行四边形
∴AB∥CD (平行四边形的定义)
AD=BC(平行四边形的对边分别相等)
∵E、F分别是AD,BC的中点
∴ED=BF,即ED BF
∥
﹦
∴四边形EBFD是平行四边形(一组对边平行且相等的四边形是平行四边形)
∴BE=DF(平行四边形的对边分别相等)
说一说:
1、请你总结平行四边形的判定方法:
2、本节课所学的解决问题的思路是:
(2)碰到平行四边形的问题常转化为三角形来解决。
(1)解决一个数学问题,常要通过“动手实践”----“ 猜想”----“验证猜想(证明)”-----“得出结论” ;
作业布置:
必做题 课本P91 7、10题
思考题 课本P92 第11题
聪明出于勤奋,天才在于积累。
-华罗庚
八年级数学备课组 邹 茜
1、掌握用“一组对边平行且相等”来判定平行四边形的方法;
2、能根据平行四边形的判别方法进行有关的证明。
一天八年级的李明同学在生物实验室做实验时,不小心碰碎了实验室的一块平行四边形的实验用的玻璃片,只剩下如图所示部分,他想去割一块赔给学校,带上玻璃剩下部分去玻璃店不安全,于是他想把原来的平行四边形重新在纸上画出来,然后带上图纸去就行了,可原来的平行四边形怎么画出来呢?(提示:A,B,C为三顶点,找出第四个顶点D即可)
A
B
C
想一想
D
A
B
C
(两组对边分别平行的四边形是平行四边形)
∵AB∥CD,AD∥BC
∴四边形ABCD是平行四边形
D
A
B
C
(两组对边分别相等的四边形是平行四边形)
∵AB=CD,AD=BC
∴四边形ABCD是平行四边形
D
O
A
B
C
(对角线互相平分的四边形是平行四边形)
∵AO=CO,BO=DO
∴四边形ABCD是平行四边形
D
A
B
C
A
B
C
D
一组对边平行且相等的四边形是平行四边形?
∵AB CD, ∴四边形ABCD是平行四边形
∥
﹦
猜想,对吗?
A
B
C
D
求证:四边形ABCD是平行四边形。
证明:连接AC
∵AD∥BC
∴∠DAC=∠ACB
又∵AD=BC,AC=AC,
∴ΔABC≌ΔCDA
∴∠BAC=∠ACD
∴AB∥CD
∴四边形ABCD是平行四边形
已知:在四边形ABCD中, AD BC。
(两组对边分别平行的四边形是平行四边形)
你还有其他证法吗?
一组对边平行且相等的四边形是平行四边形
平行四边形的判定定理4:
符号语言:
∵AB CD
∴四边形ABCD是平行四边形
(一组对边平行且相等的四边形是平行四边形)
A
B
C
D
从边判定
1、两组对边分别平行的四边形是平行四边形
2、两组对边分别相等的四边形是平行四边形
3、一组对边平行且相等的四边形是平行四边形
从角判定
两组对角分别相等的四边形是平行四边形
从对角线判定
两条对角线互相平分的四边形是平行四边形
理一理
平行四边形的判定方法
1、已知在四边形ABCD中,AD∥BC,要使这个四边形为平行四边形,则需添加一个你认为正确的条件为 ( )
A B∥DC,或∠A =∠C或AD=BC
2、能判定一个四边形是平行四边形的条件是( )
A、一组对角相等 B、一组对边平行且相等
C、一对邻角互补 D、两条对角线互相垂直
B
3、四边形ABCD中,若∠A = ∠C,∠B = ∠D,则下列结论中错误的是( )
C
A、AB = CD B、AD∥BC
C、∠A = ∠B D、对角线互相平分
4、如图,在 ABCD的一组对边AD、BC上截取EF=MN,连接EM、FN,那么EM和FN有怎样的关系?为什么?
A
B
C
D
E
F
M
N
5、已知:如图,E、F分别是 ABCD 的边AD,BC的中点。
求证:BE=DF.
D
F
E
C
B
A
证明:
∵四边形ABCD是平行四边形
∴AB∥CD (平行四边形的定义)
AD=BC(平行四边形的对边分别相等)
∵E、F分别是AD,BC的中点
∴ED=BF,即ED BF
∥
﹦
∴四边形EBFD是平行四边形(一组对边平行且相等的四边形是平行四边形)
∴BE=DF(平行四边形的对边分别相等)
说一说:
1、请你总结平行四边形的判定方法:
2、本节课所学的解决问题的思路是:
(2)碰到平行四边形的问题常转化为三角形来解决。
(1)解决一个数学问题,常要通过“动手实践”----“ 猜想”----“验证猜想(证明)”-----“得出结论” ;
作业布置:
必做题 课本P91 7、10题
思考题 课本P92 第11题
