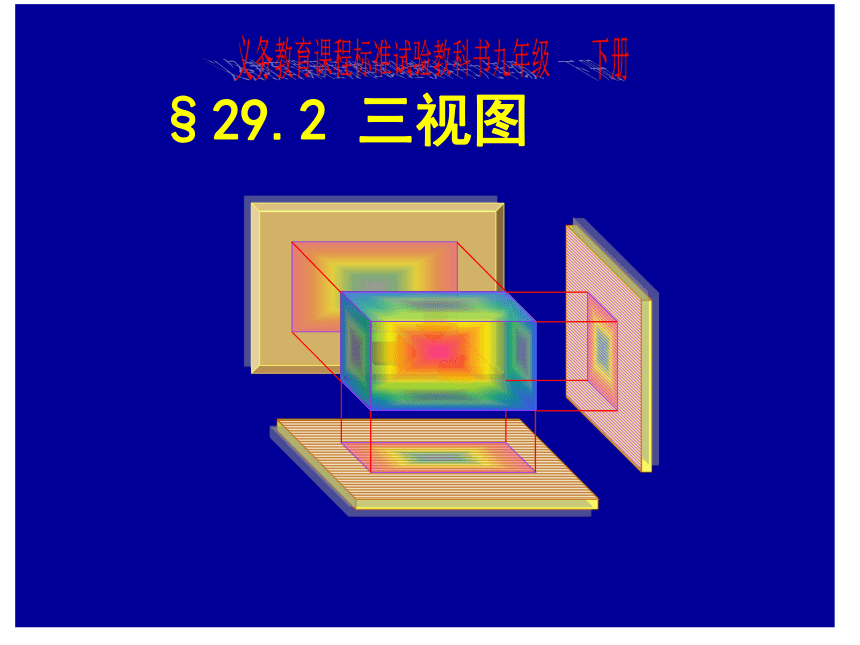
§29.2 三视图
图片预览


文档简介
(共47张PPT)
§29.2 三视图
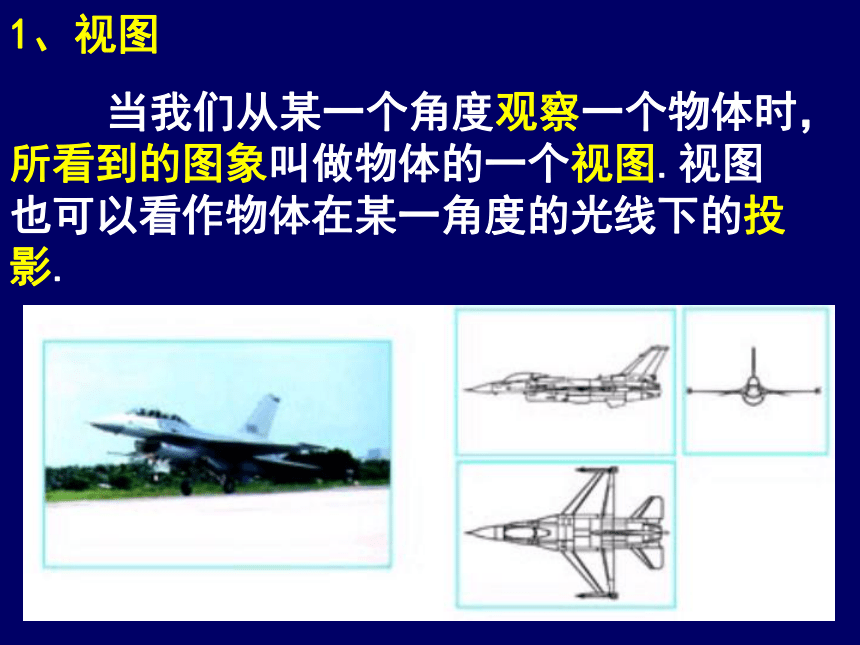
1、视图
当我们从某一个角度观察一个物体时,所看到的图象叫做物体的一个视图.视图也可以看作物体在某一角度的光线下的投影.
你能说出这三个视图分别是从哪个方向观察这本书得到的吗?
正面
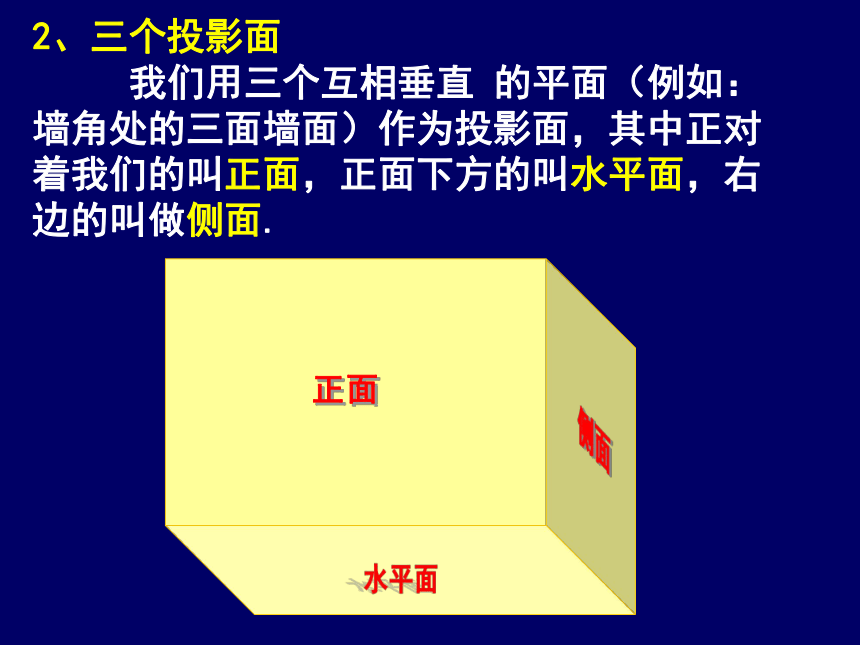
2、三个投影面
我们用三个互相垂直 的平面(例如:墙角处的三面墙面)作为投影面,其中正对着我们的叫正面,正面下方的叫水平面,右边的叫做侧面.
主视图
主视图
俯视图
左视图
正面
从上面看
从正面看
从左面看
高
长
宽
宽
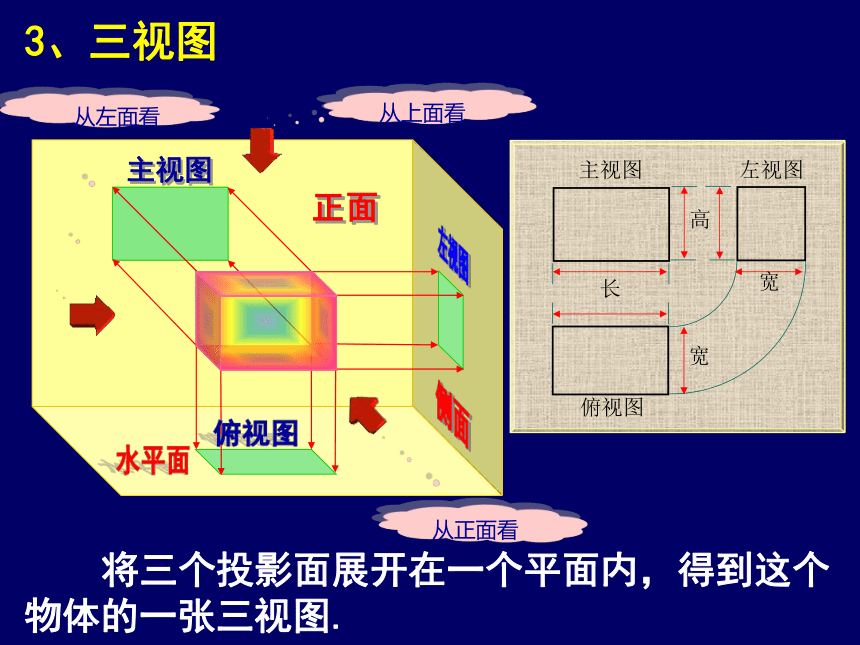
3、三视图
将三个投影面展开在一个平面内,得到这个物体的一张三视图.
主视图
俯视图
左视图
高
长
宽
宽
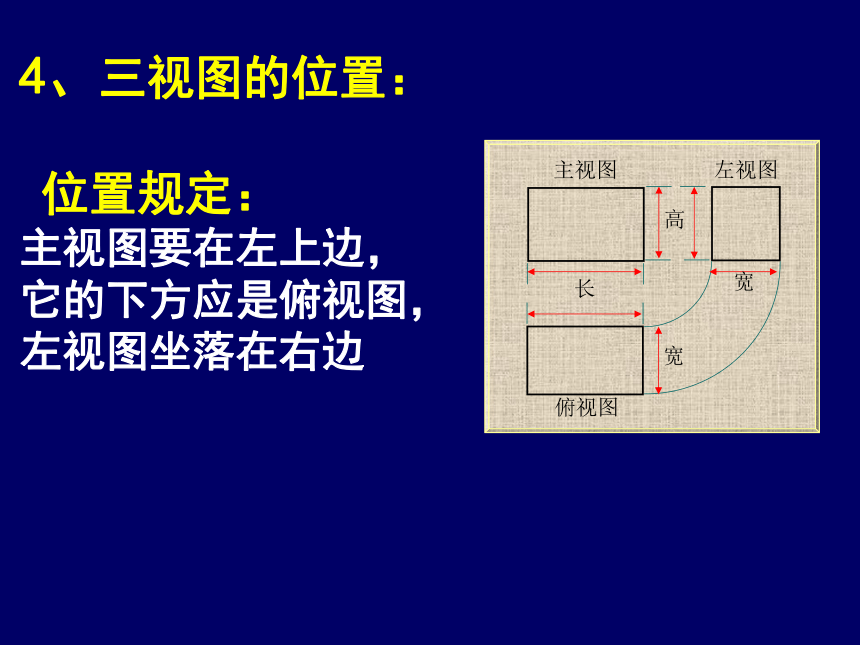
4、三视图的位置:
位置规定:
主视图要在左上边,
它的下方应是俯视图,
左视图坐落在右边
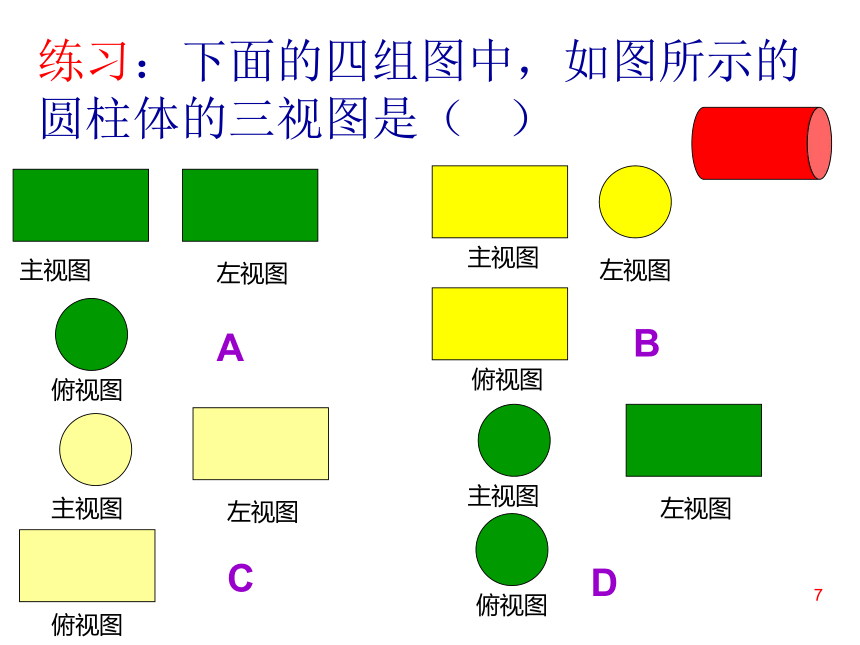
练习:下面的四组图中,如图所示的圆柱体的三视图是( )
主视图
左视图
俯视图
A
主视图
左视图
俯视图
B
主视图
左视图
俯视图
C
主视图
左视图
俯视图
D
主视图
主视图
左视图
正面
高
长
宽
宽
俯视图
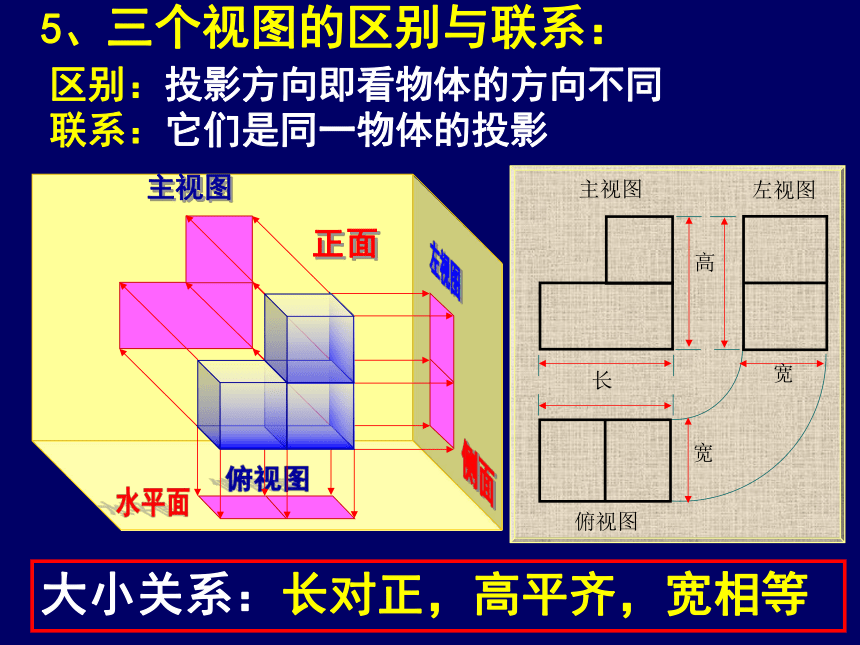
5、三个视图的区别与联系:
区别:投影方向即看物体的方向不同
联系:它们是同一物体的投影
大小关系:长对正,高平齐,宽相等
主视图
左视图
高
长
宽
宽
俯视图
高平齐
长对正
宽相等
正方形
正方形
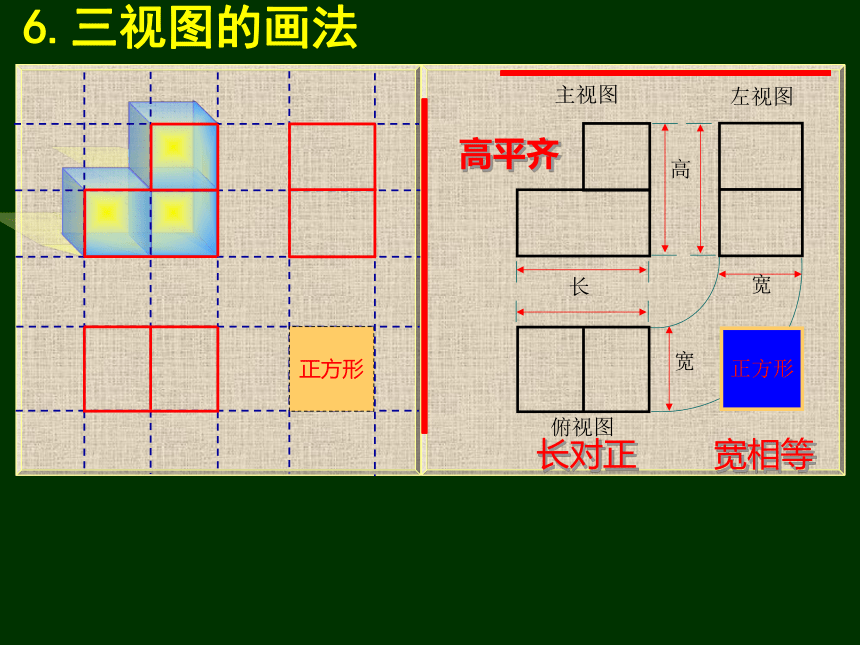
6.三视图的画法
你能画出正方体的三视图吗?
主 视 图
左 视 图
俯 视 图
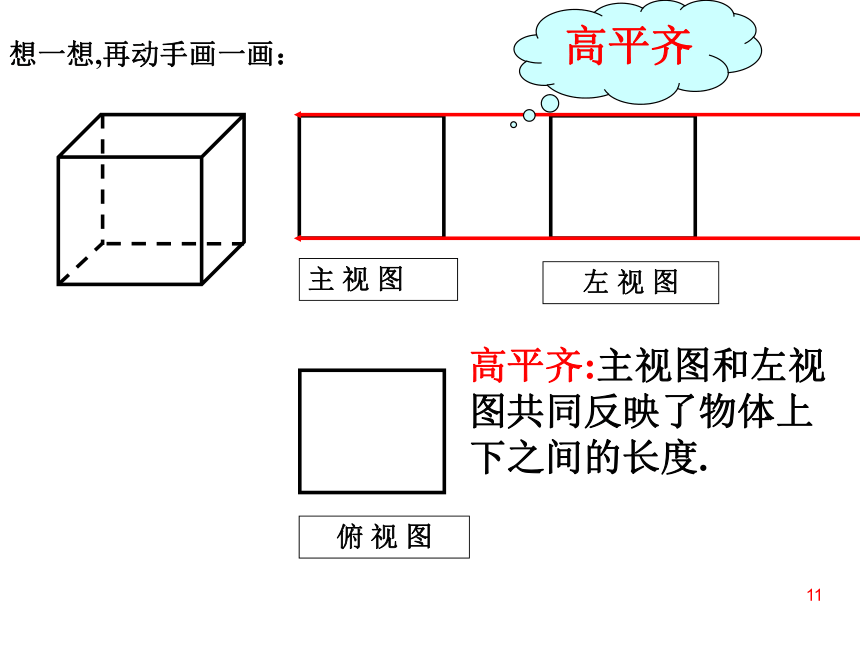
想一想,再动手画一画:
高平齐
高平齐:主视图和左视图共同反映了物体上下之间的长度.
主 视 图
左 视 图
俯 视 图
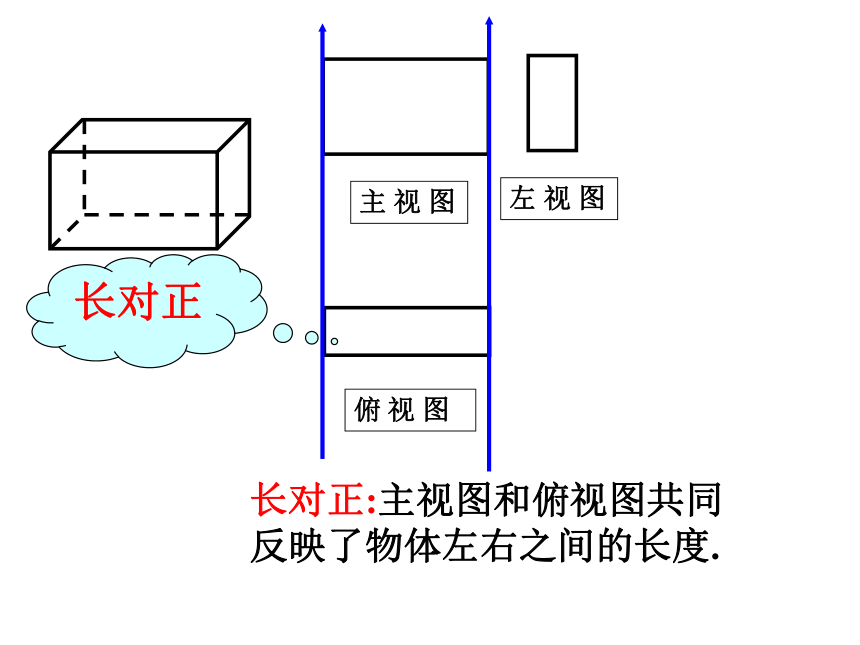
长对正
长对正:主视图和俯视图共同反映了物体左右之间的长度.
你会画圆柱的三视图吗?试一试吧!
试一试
主 视 图
左 视 图
俯 视 图
宽相等
宽相等:俯视图和左视图共同反映了物体前后之间的长度.
画出如图所示四棱锥的三视图。
挑战自我
主 视 图
左 视 图
俯 视 图
我相信你一定能画出这个复杂几何体的三视图!
1、画出下列立体图形的三视图.
2、指出左面三个平面图形是右面这个物体的三视图中
的哪个视图.
(
(
(
主视图)
俯视图)
左视图)
练一练
例2:画出下图支架的三视图,支架的两个台阶的高度和宽度都是同一长度.
解: 如图是支架的三视图
例3:
下图是一根钢管的直观图,画出它的三视图.
解:如图是钢管的三视图,其中的虚线表示钢管的内壁.
三视图
1、三视图
主视图——从正面看到的图
左视图——从左面看到的图
俯视图——从上面看到的图
2、画物体的三视图时,要符合如下原则:
主视图 左视图
俯视图
大小:长对正,高平齐,宽相等.
小结 反馈
位置:
小结3:三视图的画法
(1)先画主视图,在主视图正下方画出俯视图,注意与主视图“长对正”,在主视图正右方画出左视图,注意与主视图“高平齐”,与俯视图“宽相等”.
(2)看得见部分的轮廓线画成实线,因被其他部分遮挡而看不见部分的轮廓线画成虚线.
小结4:基本几何体的三视图
1.柱体——有两个视图是矩形.
2.锥体——有两个视图是三角形.
3.台体
圆台——有两个视图是等腰梯形
棱台——有两个视图是梯形
4.球——三个视图都是圆
练习1 画出图中几何体的三视图
练习1 画出图中几何体的三视图
回顾:基本几何体的三视图
1.柱体——有两个视图是矩形.
2.锥体——有两个视图是三角形.
3.台体
圆台——有两个视图是等腰梯形
棱台——有两个视图是梯形
4.球——三个视图都是圆
例4 根据三视图说出立体图形的名称
例5 根据物体的三视图,描述物体的形状.
练习1:由三视图想象实物形状
练习1:由三视图想象实物形状
练习2:根据下面的三视图说出这个几何体是怎样由四个正方体组合而成的.
练习3:根据三视图描述物体的形状
练习3:根据三视图描述物体的形状
练习3:根据三视图描述物体的形状
练习3:根据三视图描述物体的形状
练习4:
根据三视图,确定立体图形是由哪些基本几何体通过何种方式组合而成的.
练习4:
根据三视图,确定立体图形是由哪些基本几何体通过何种方式组合而成的.
练习4:
根据三视图,确定立体图形是由哪些基本几何体通过何种方式组合而成的.
练习4:
根据三视图,确定立体图形是由哪些基本几何体通过何种方式组合而成的.
投影规律
主视图反映了物体上下、左右的位置关系,即反映了物体的高度和长度;俯视图反映了物体左右、前后的位置关系,即反映了物体的长度和宽度;左视图反映了物体上下、前后的位置关系,即反映了物体的高度和宽度.由此可得出三视图之间的投影规律为:
主、俯视图——长对正;
主、左视图——高平齐;
俯、左视图——宽相等.
【探究】
1、如右图是由几个小立方体所搭几何体的俯视图,小正方形中的数字表示在该位置小正方体的个数。
探究
你能摆出这个几何体吗?
试画出这个几何体的主视图与左视图。
主视图:
左视图:
1
1
2
2
1
1
2
2
主视图:
左视图:
思考方法
先根据俯视图确定主视图有 列,
3
再根据数字确定每列的方块有 个,
不用摆出这个几何体,你能画出这个几何体的主视图与左视图吗?
主视图有 列,
第一列的方块有 个,
1
第二列的方块有 个,
2
第三列的方块有 个,
1
左视图有 列,
2
第一列的方块有 个,
2
第二列的方块有 个,
2
【反思】
2、你能由三视图得到该几何体吗?
3、你会由“给出数字的俯视图”画出几何体的主视图、左视图吗?
1、你能画出一个几何体的三视图吗?
动手设计
请画出下面立体图形的三视图。
俯视方向
注意:根据“长对正,高平齐,宽相等” 画
三视图必须遵循的法则作图。
辨一辨,说一说:
1、一个几何体的视图是唯一的,但从视图反过来考虑几何体时,它有多种可能性。请你举一些例子加以说明.
提示:例如正方体的主视图是一个正方形,但主视图是正方形的几何体就有很多,如四棱柱,长方体,圆柱等.
§29.2 三视图
1、视图
当我们从某一个角度观察一个物体时,所看到的图象叫做物体的一个视图.视图也可以看作物体在某一角度的光线下的投影.
你能说出这三个视图分别是从哪个方向观察这本书得到的吗?
正面
2、三个投影面
我们用三个互相垂直 的平面(例如:墙角处的三面墙面)作为投影面,其中正对着我们的叫正面,正面下方的叫水平面,右边的叫做侧面.
主视图
主视图
俯视图
左视图
正面
从上面看
从正面看
从左面看
高
长
宽
宽
3、三视图
将三个投影面展开在一个平面内,得到这个物体的一张三视图.
主视图
俯视图
左视图
高
长
宽
宽
4、三视图的位置:
位置规定:
主视图要在左上边,
它的下方应是俯视图,
左视图坐落在右边
练习:下面的四组图中,如图所示的圆柱体的三视图是( )
主视图
左视图
俯视图
A
主视图
左视图
俯视图
B
主视图
左视图
俯视图
C
主视图
左视图
俯视图
D
主视图
主视图
左视图
正面
高
长
宽
宽
俯视图
5、三个视图的区别与联系:
区别:投影方向即看物体的方向不同
联系:它们是同一物体的投影
大小关系:长对正,高平齐,宽相等
主视图
左视图
高
长
宽
宽
俯视图
高平齐
长对正
宽相等
正方形
正方形
6.三视图的画法
你能画出正方体的三视图吗?
主 视 图
左 视 图
俯 视 图
想一想,再动手画一画:
高平齐
高平齐:主视图和左视图共同反映了物体上下之间的长度.
主 视 图
左 视 图
俯 视 图
长对正
长对正:主视图和俯视图共同反映了物体左右之间的长度.
你会画圆柱的三视图吗?试一试吧!
试一试
主 视 图
左 视 图
俯 视 图
宽相等
宽相等:俯视图和左视图共同反映了物体前后之间的长度.
画出如图所示四棱锥的三视图。
挑战自我
主 视 图
左 视 图
俯 视 图
我相信你一定能画出这个复杂几何体的三视图!
1、画出下列立体图形的三视图.
2、指出左面三个平面图形是右面这个物体的三视图中
的哪个视图.
(
(
(
主视图)
俯视图)
左视图)
练一练
例2:画出下图支架的三视图,支架的两个台阶的高度和宽度都是同一长度.
解: 如图是支架的三视图
例3:
下图是一根钢管的直观图,画出它的三视图.
解:如图是钢管的三视图,其中的虚线表示钢管的内壁.
三视图
1、三视图
主视图——从正面看到的图
左视图——从左面看到的图
俯视图——从上面看到的图
2、画物体的三视图时,要符合如下原则:
主视图 左视图
俯视图
大小:长对正,高平齐,宽相等.
小结 反馈
位置:
小结3:三视图的画法
(1)先画主视图,在主视图正下方画出俯视图,注意与主视图“长对正”,在主视图正右方画出左视图,注意与主视图“高平齐”,与俯视图“宽相等”.
(2)看得见部分的轮廓线画成实线,因被其他部分遮挡而看不见部分的轮廓线画成虚线.
小结4:基本几何体的三视图
1.柱体——有两个视图是矩形.
2.锥体——有两个视图是三角形.
3.台体
圆台——有两个视图是等腰梯形
棱台——有两个视图是梯形
4.球——三个视图都是圆
练习1 画出图中几何体的三视图
练习1 画出图中几何体的三视图
回顾:基本几何体的三视图
1.柱体——有两个视图是矩形.
2.锥体——有两个视图是三角形.
3.台体
圆台——有两个视图是等腰梯形
棱台——有两个视图是梯形
4.球——三个视图都是圆
例4 根据三视图说出立体图形的名称
例5 根据物体的三视图,描述物体的形状.
练习1:由三视图想象实物形状
练习1:由三视图想象实物形状
练习2:根据下面的三视图说出这个几何体是怎样由四个正方体组合而成的.
练习3:根据三视图描述物体的形状
练习3:根据三视图描述物体的形状
练习3:根据三视图描述物体的形状
练习3:根据三视图描述物体的形状
练习4:
根据三视图,确定立体图形是由哪些基本几何体通过何种方式组合而成的.
练习4:
根据三视图,确定立体图形是由哪些基本几何体通过何种方式组合而成的.
练习4:
根据三视图,确定立体图形是由哪些基本几何体通过何种方式组合而成的.
练习4:
根据三视图,确定立体图形是由哪些基本几何体通过何种方式组合而成的.
投影规律
主视图反映了物体上下、左右的位置关系,即反映了物体的高度和长度;俯视图反映了物体左右、前后的位置关系,即反映了物体的长度和宽度;左视图反映了物体上下、前后的位置关系,即反映了物体的高度和宽度.由此可得出三视图之间的投影规律为:
主、俯视图——长对正;
主、左视图——高平齐;
俯、左视图——宽相等.
【探究】
1、如右图是由几个小立方体所搭几何体的俯视图,小正方形中的数字表示在该位置小正方体的个数。
探究
你能摆出这个几何体吗?
试画出这个几何体的主视图与左视图。
主视图:
左视图:
1
1
2
2
1
1
2
2
主视图:
左视图:
思考方法
先根据俯视图确定主视图有 列,
3
再根据数字确定每列的方块有 个,
不用摆出这个几何体,你能画出这个几何体的主视图与左视图吗?
主视图有 列,
第一列的方块有 个,
1
第二列的方块有 个,
2
第三列的方块有 个,
1
左视图有 列,
2
第一列的方块有 个,
2
第二列的方块有 个,
2
【反思】
2、你能由三视图得到该几何体吗?
3、你会由“给出数字的俯视图”画出几何体的主视图、左视图吗?
1、你能画出一个几何体的三视图吗?
动手设计
请画出下面立体图形的三视图。
俯视方向
注意:根据“长对正,高平齐,宽相等” 画
三视图必须遵循的法则作图。
辨一辨,说一说:
1、一个几何体的视图是唯一的,但从视图反过来考虑几何体时,它有多种可能性。请你举一些例子加以说明.
提示:例如正方体的主视图是一个正方形,但主视图是正方形的几何体就有很多,如四棱柱,长方体,圆柱等.
