正方形的性质和判定
图片预览






文档简介
(共37张PPT)
思考:1、在第四章中我们已经学习了哪些特殊的四边形?
平行四边形、矩形、菱形。
思考:2、分别叙述这三种四边形的定义。
复习
邻边
相等
有一个角
是直角
两组对边
分别平行
有一个角是直角
有一组邻边相等
四边形
平行四边形
矩形
菱形
矩 形
?
菱形
?
正 方 形
正方形
矩形
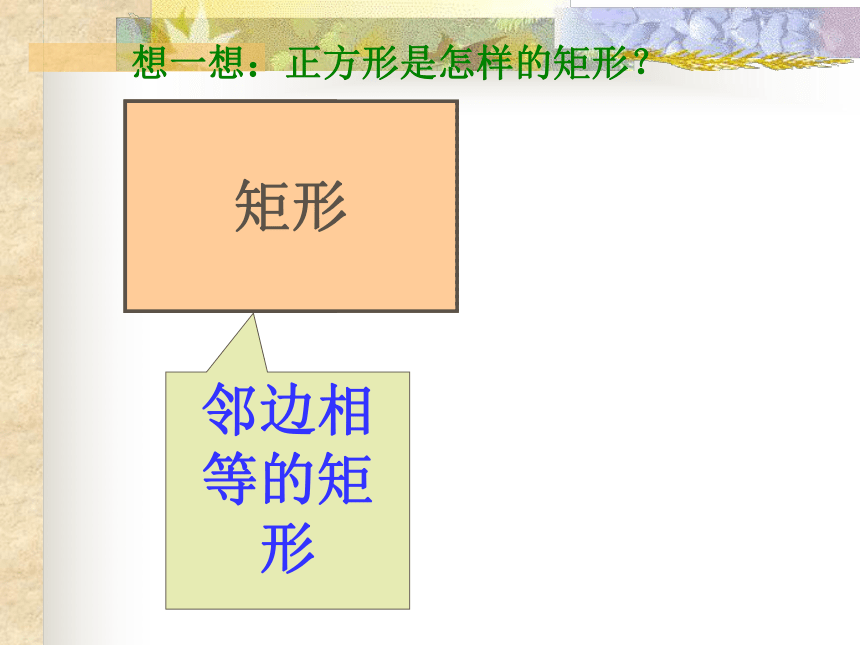
邻边相等的矩形
想一想:正方形是怎样的矩形?
菱形
正方形
一个角是直角的菱形
想一想:正方形是怎样的菱形?
⑴有一组邻边相等的平行四边形(菱形)
⑵并且有一个角是直角的平行四边形(矩形)
两层含义
正方形
有一组邻边相等并且有一个角是直角的平行四边形
有一组邻边相等的矩形叫做正方形。
1.正方形定义:
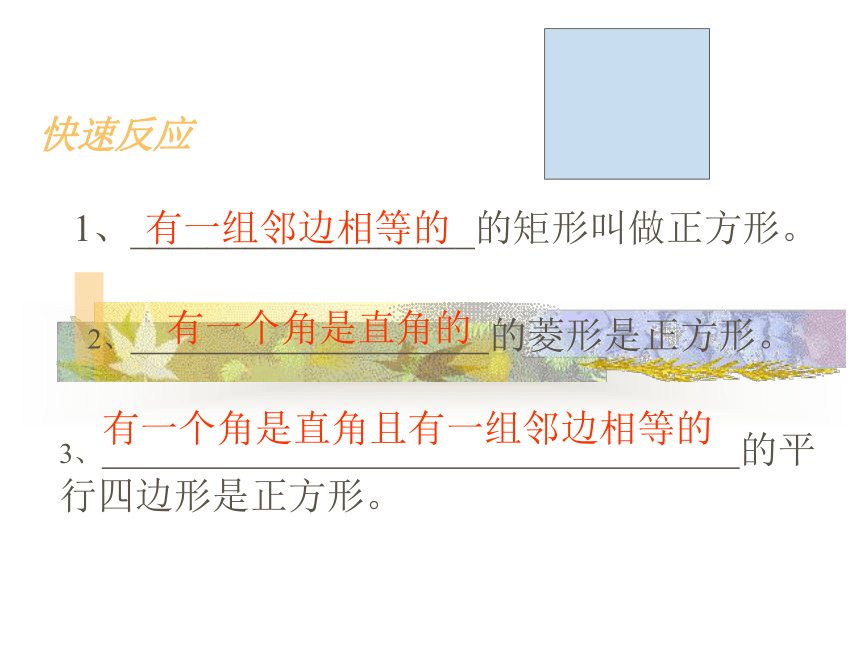
1、__________________的矩形叫做正方形。
快速反应
有一组邻边相等的
2、 的菱形是正方形。
有一个角是直角的
3、 的平行四边形是正方形。
有一个角是直角且有一组邻边相等的
2、正方形的性质
边
对角线
对边平行
四边相等
对角线相等
互相垂直平分
每条对角线平分一组对角
四个角相等且都是直角
角
正方形性质
正方形具有平行四边形、矩形、菱 形的一切性质。
正方形的性质定理1:正方形的四个角都是直角,四条边都
相等且对边平行。
正方形的性质定理2:正方形的两条对角线相等,并且互相
垂直 平分,每条对角线平分一组对角。
二、正方形的性质
三段论形式:
∵四边形ABCD是正方形
∴∠DAB=∠ABC =∠BCD =∠CDA=90°
∴AB=BC=CD=DA
∴AD∥BC,AB∥CD
∴AC =BD,AC⊥BD,AO = CO = BO = DO
∴AC平分∠BAD和∠BCD
∴BD平分 ∠ ABD和∠ADC
A
D
B
C
O
对称轴
平行四边形
矩形
菱形
正
方
形
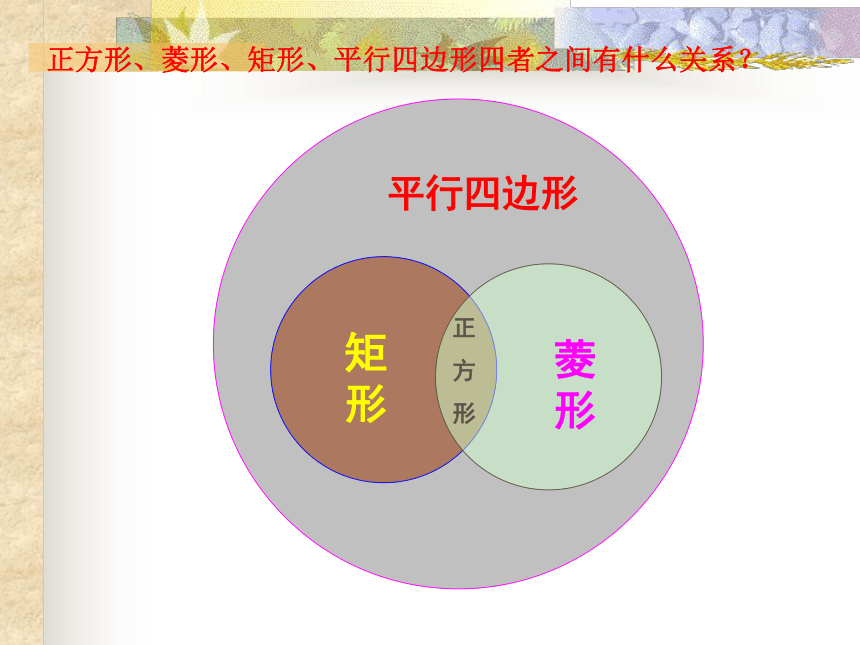
正方形、菱形、矩形、平行四边形四者之间有什么关系?
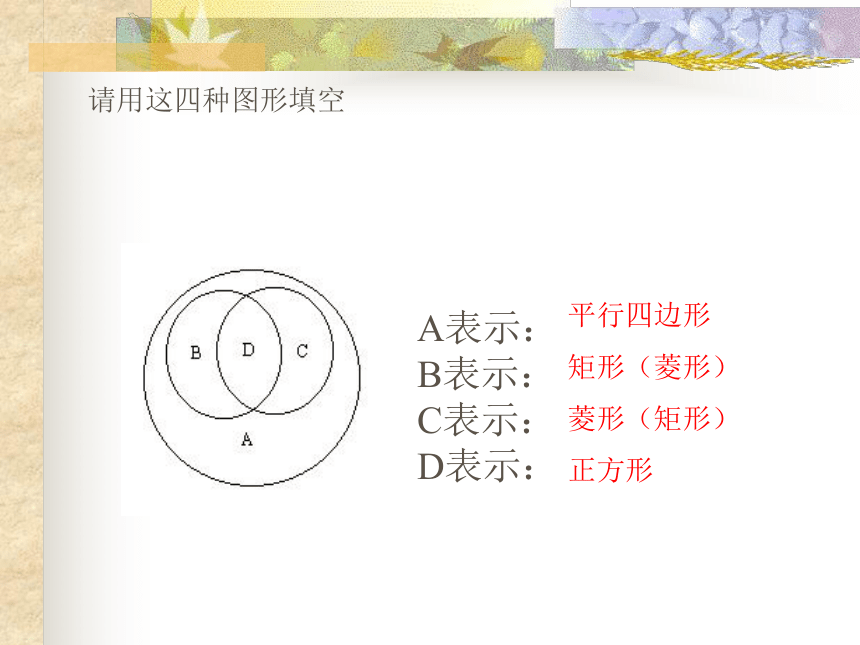
请用这四种图形填空
A表示:B表示:C表示:D表示:
平行四边形
矩形(菱形)
菱形(矩形)
正方形
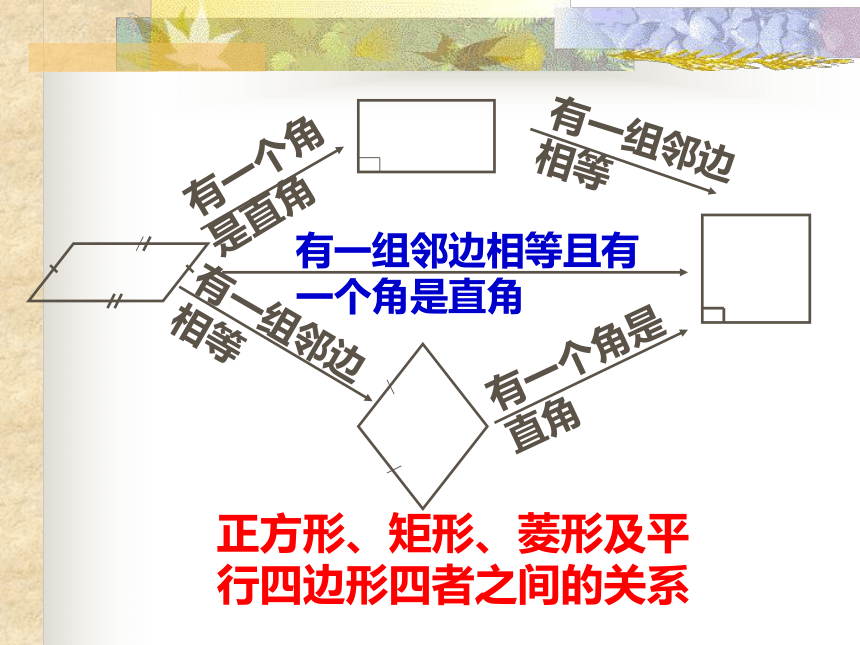
有一个角是直角
有一组邻边相等
有一组邻边相等
有一个角是直角
有一组邻边相等且有一个角是直角
正方形、矩形、菱形及平行四边形四者之间的关系
3、正方形的判定:
1.定义法
2.先判定是矩形,再判定是菱形,或先判定是菱形,再判定是矩形。
A
D
C
B
O
正方形对角线把正方形分成多少个等腰直角三角形?
拓展讨论:
结论:
分成八个等腰直角三角形,分别是△ABC、 △ADC、 △ABD、 △BCD ;
△AOB、 △BOC、 △COD、 △DOA.
例题1:四边形ABCD是正方形,两条对角线相交于点O,(1)求∠AOB,∠OAB的度数。
8
解:∵四边形ABCD是正方形
∴AC⊥BD ∠AOB=900
∠BAC=∠DAC
∴∠OAB=450
A
B
C
D
O
E
F
(2)若AC=4,则正方形边长 ; 正方形的面积是
4㎝
(3)正方形的面积64cm2,则对角线交点到正方形一边的距离
2√2
例2求证:正方形的两条对角线把正方形分成四个全等的 等腰直角三角形。
已知:四边形ABCD是正方形,对角
线AC、BD相交于点O
求证:⊿ABO、 ⊿ BCO 、 ⊿ CDO、
⊿ DAO是全等的等腰直角三角形
证明:∵四边形ABCD是正方形
A
D
B
C
O
由于正方形的面积等于⊿ABO 面积的4倍,所以正方形的面积等于对角线的平方的一半。
∴AC=BD,AC⊥BD,AO = CO = BO = DO
﹙正方形的对角线相等,并且互相垂直平分﹚
∴⊿ABO、 ⊿ BCO 、 ⊿ CDO、 ⊿ DAO 都是等腰直角三角形,并且⊿ABO ≌⊿ BCO ≌ ⊿ CDO ≌ ⊿ DAO
补充练习:
1、如图,正方形ABCD的边长为4cm,则图中阴影部分的面积为 平方厘米.
A
B
C
D
2、如图,在等腰Rt△ABC中,∠C=90°,正方形DEFG的顶点D在边AC上,点E、F在边AB上,点G在边BC上.
(1)求证AE=BF;
(2)若BC= cm,求正方形DEFG的边长.
2、周长为20cm的正方形,边长是 对角线长是 面积是 。
1)一组邻边相等,一个角是直角的四边形是正方形。
2)对角线互相垂直平分且相等的四边形是正方形。
自我检测
1、下列说法对吗?
5㎝
25cm2
A
B
C
D
O
3、如图,有 个等腰直角三角形
8
5√2 cm
作 业
补充习题:1、已知正方形ABCD的边长为4,E为BC边上一点,且BE=1,P为AC上一点,求PE+PB的最小值.
2、在正方形ABCD中,AC是对角线,AE平分∠BAC,试猜想AB、AC、BE之间的关系,并证明你的猜想.
G
F
E
D
A
B
C
解:∵四边形ABCD是正方形
∴AB= BC = 2cm,∠ABC = 90°
﹙正方形的四个角都是直角,四条边都相等﹚
练习 1、已知:正方形的一条边长为2cm,求这个正方形
的周长、对角线长和正方形的面积。
A
D
B
C
∵边长AB=2cm
∴周长C=4AB=8cm
练习 2、已知:正方形的一条对角线长为4cm
解:∵四边形ABCD是正方形
∴AB = BC,∠ABC=90°
﹙正方形的四个角都是直角,四条边都相等﹚
A
D
B
C
1、正方形的面积等于边长的平方。
2、正方形的面积等于等于对角线的平方的一半。
3、正方形的周长等于边长的4倍。
在Rt⊿ABC中,
求: 它的边长和面积。
练习3、已知:在正方形ABCD中,E、F分别在BC、DC
上,且BE = DF,AC与BC相交于O点,EF
与AC相交于P点
求证:EF ⊥ AC,EF ∥ BD
证明: ∵四边形ABCD是正方形
∴BC = CD
﹙ 正方形的四条边都相等﹚
∵BE = DF
∴EC = FC
∵AC平分∠BCD
﹙ 正方形的每条对角线平分一组对角﹚
∴EF⊥ AC
∵AC ⊥BD
(正方形的对角线互相垂直)
∴ EF ∥ BD
A
B
C
D
O
P
F
E
矩形、正方形(2)
4、判断。
(1)正方形一定是矩形。( )
(2)正方形一定是菱形。( )
(3)菱形一定是正方形。( )
(4)矩形一定是正方形。( )
(5)正方形、矩形、菱形都是平行四边形。( )
快速反应
矩形、正方形(2)
1、在下列性质中,平行四边形具有的是_______,矩形具有的是_________,菱形具有的是_______,正方形具有的是_______________。
(1)四边都相等; (2)对角线互相平分;
(3)对角线相等; (4)对角线互相垂直;
(5)四个角都是直角;
(6)每条对角线平分一组对角;
(7)对边相等且平行;
(8)有两条对称轴。
自主学习
矩形、正方形(2)
2、正方形两条对角线的和为8cm,它的面积为____________.
自主学习
矩形、正方形(2)
3、如图,点E、F在正方形ABCD的边BC、CD上,BE=CF.
(1)AE与BF相等吗?为什么?
(2)AE与BF是否垂直?说明你的理由。
自主学习
尝试练习:
(1)已知:如图,ABCD和AKLM都是正方形,求证:MD=KB。
尝试练习:
(2)如图,正方形ABCD中,AC交BD于O,点M、N分别在AC、BD上,且OM=ON,
求证:BM=CN。
如何设计花坛?
在一块正方形的花坛上,欲修建两条直的小路,使得两条直的小路将花坛平均分成面积相等的四部分(不考虑道路的宽度),你有几种方法?(至少说出三种)
请你当设计师
应用举例:
A
B
C
D
C/
A/
B/
D/
已知:如图点A' 、 B' 、 C'、D'分别是正方形ABCD
四条边上的点,并且AA'=BB'=CC'=DD'
求证:四边形A'B'C'D'是正方形
①、由已知正方形证三角形全等;
②、证得菱形;
③、再证直角;
④、是正方形
证题思路分析
上一页
例1 已知:如图,在正方形ABCD中,A`A=B`B=C`C=D`D 。
求证:四边形A`B`C`D`是正方形。
证明:∵四边形ABCD是正方形 ∴AB=BC=CD=DA
又∵A`A=B`B=C`C=D`D ∴D`A=A`B=B`C=C`D
∵∠A=∠B=∠C=∠D=90° ∴△AA`D`≌△BB`A`≌△CC`B`≌△DD`C`
∴四边形A`B`C`D`是菱形
又∵∠AD`A`=∠BA`B`, ∠ AA`D`+∠AD`A`=90°
∴ ∠AA`D`+∠BA`B`=90 °
∵∠D`A`B`=180°—(∠AA`D`+∠BA`B`)=90°
∴四边形A`B`C`D`是正方形。
例2已知:如图,在矩形ABCD中,AF,BH,CH,DF分别是各内角平分线,AF和BH交于E,CH和DF交于G。 求证:四边形EFGH是正方形
A D
H
B C
F
E
G
证明:∵AD∥BC,AF、BH是角平分线
∴AF⊥BH
同理 BH⊥CH
CH⊥DF DF⊥AF
∴∠HEF=∠EFG=
∠FGH=∠GHE=90°∴四边形EFGH是矩形
A
B
C
D
E
F
G
H
∵AF平分∠BAD ∴∠BAF=∠DAF=45°
同理∠ABH=∠CBH=45°
∠BCH=∠DCH=45°
∠CDF=∠ADF=45°
∵∠DAF=∠CBH
AD=BC
∠ADF=∠BCH
∴△AFD≌△BHC(ASA)
∴AF=BH
∵∠BAF=∠ABH
∴AE=BE
∴EH=EF
∴四边形EFGH是正方形
课堂练习:
1、已知:正方形ABCD中,分别过A、C两点作a∥b,作BM⊥a于M,DN⊥a于N,直线MB、ND分别交b于Q、P。求证:四边形PNMQ是正方形。
2 、已知:如图,正方形ABCD和正方形CEFG,延长CD到H,且DH=CE=BK。求证:四边形AKFH是一个正方形
A
B
C
D
K
F
H
E
G
数学家庭作业:1、课时第65页到67页,
2、五洲导学第46页到47页。
思考:1、在第四章中我们已经学习了哪些特殊的四边形?
平行四边形、矩形、菱形。
思考:2、分别叙述这三种四边形的定义。
复习
邻边
相等
有一个角
是直角
两组对边
分别平行
有一个角是直角
有一组邻边相等
四边形
平行四边形
矩形
菱形
矩 形
?
菱形
?
正 方 形
正方形
矩形
邻边相等的矩形
想一想:正方形是怎样的矩形?
菱形
正方形
一个角是直角的菱形
想一想:正方形是怎样的菱形?
⑴有一组邻边相等的平行四边形(菱形)
⑵并且有一个角是直角的平行四边形(矩形)
两层含义
正方形
有一组邻边相等并且有一个角是直角的平行四边形
有一组邻边相等的矩形叫做正方形。
1.正方形定义:
1、__________________的矩形叫做正方形。
快速反应
有一组邻边相等的
2、 的菱形是正方形。
有一个角是直角的
3、 的平行四边形是正方形。
有一个角是直角且有一组邻边相等的
2、正方形的性质
边
对角线
对边平行
四边相等
对角线相等
互相垂直平分
每条对角线平分一组对角
四个角相等且都是直角
角
正方形性质
正方形具有平行四边形、矩形、菱 形的一切性质。
正方形的性质定理1:正方形的四个角都是直角,四条边都
相等且对边平行。
正方形的性质定理2:正方形的两条对角线相等,并且互相
垂直 平分,每条对角线平分一组对角。
二、正方形的性质
三段论形式:
∵四边形ABCD是正方形
∴∠DAB=∠ABC =∠BCD =∠CDA=90°
∴AB=BC=CD=DA
∴AD∥BC,AB∥CD
∴AC =BD,AC⊥BD,AO = CO = BO = DO
∴AC平分∠BAD和∠BCD
∴BD平分 ∠ ABD和∠ADC
A
D
B
C
O
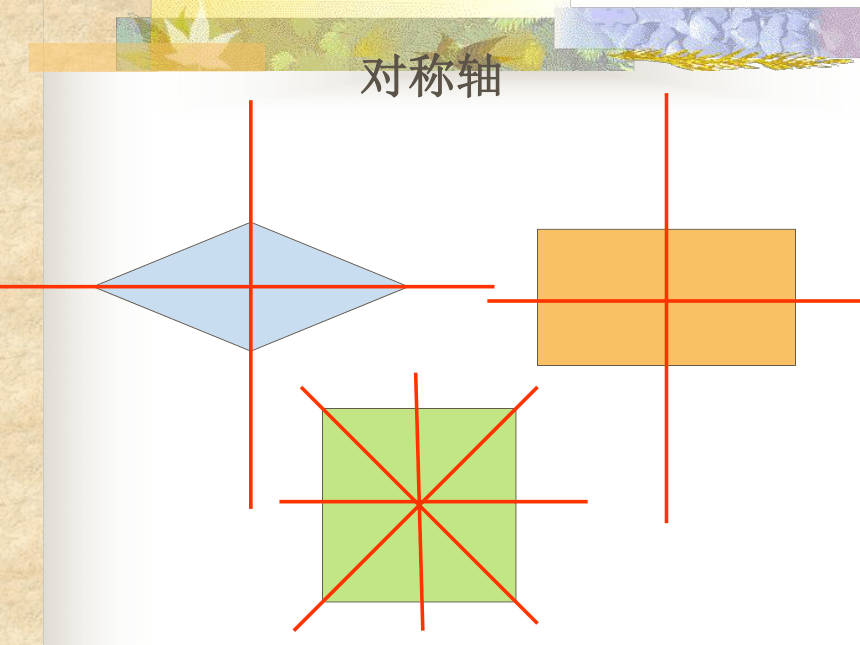
对称轴
平行四边形
矩形
菱形
正
方
形
正方形、菱形、矩形、平行四边形四者之间有什么关系?
请用这四种图形填空
A表示:B表示:C表示:D表示:
平行四边形
矩形(菱形)
菱形(矩形)
正方形
有一个角是直角
有一组邻边相等
有一组邻边相等
有一个角是直角
有一组邻边相等且有一个角是直角
正方形、矩形、菱形及平行四边形四者之间的关系
3、正方形的判定:
1.定义法
2.先判定是矩形,再判定是菱形,或先判定是菱形,再判定是矩形。
A
D
C
B
O
正方形对角线把正方形分成多少个等腰直角三角形?
拓展讨论:
结论:
分成八个等腰直角三角形,分别是△ABC、 △ADC、 △ABD、 △BCD ;
△AOB、 △BOC、 △COD、 △DOA.
例题1:四边形ABCD是正方形,两条对角线相交于点O,(1)求∠AOB,∠OAB的度数。
8
解:∵四边形ABCD是正方形
∴AC⊥BD ∠AOB=900
∠BAC=∠DAC
∴∠OAB=450
A
B
C
D
O
E
F
(2)若AC=4,则正方形边长 ; 正方形的面积是
4㎝
(3)正方形的面积64cm2,则对角线交点到正方形一边的距离
2√2
例2求证:正方形的两条对角线把正方形分成四个全等的 等腰直角三角形。
已知:四边形ABCD是正方形,对角
线AC、BD相交于点O
求证:⊿ABO、 ⊿ BCO 、 ⊿ CDO、
⊿ DAO是全等的等腰直角三角形
证明:∵四边形ABCD是正方形
A
D
B
C
O
由于正方形的面积等于⊿ABO 面积的4倍,所以正方形的面积等于对角线的平方的一半。
∴AC=BD,AC⊥BD,AO = CO = BO = DO
﹙正方形的对角线相等,并且互相垂直平分﹚
∴⊿ABO、 ⊿ BCO 、 ⊿ CDO、 ⊿ DAO 都是等腰直角三角形,并且⊿ABO ≌⊿ BCO ≌ ⊿ CDO ≌ ⊿ DAO
补充练习:
1、如图,正方形ABCD的边长为4cm,则图中阴影部分的面积为 平方厘米.
A
B
C
D
2、如图,在等腰Rt△ABC中,∠C=90°,正方形DEFG的顶点D在边AC上,点E、F在边AB上,点G在边BC上.
(1)求证AE=BF;
(2)若BC= cm,求正方形DEFG的边长.
2、周长为20cm的正方形,边长是 对角线长是 面积是 。
1)一组邻边相等,一个角是直角的四边形是正方形。
2)对角线互相垂直平分且相等的四边形是正方形。
自我检测
1、下列说法对吗?
5㎝
25cm2
A
B
C
D
O
3、如图,有 个等腰直角三角形
8
5√2 cm
作 业
补充习题:1、已知正方形ABCD的边长为4,E为BC边上一点,且BE=1,P为AC上一点,求PE+PB的最小值.
2、在正方形ABCD中,AC是对角线,AE平分∠BAC,试猜想AB、AC、BE之间的关系,并证明你的猜想.
G
F
E
D
A
B
C
解:∵四边形ABCD是正方形
∴AB= BC = 2cm,∠ABC = 90°
﹙正方形的四个角都是直角,四条边都相等﹚
练习 1、已知:正方形的一条边长为2cm,求这个正方形
的周长、对角线长和正方形的面积。
A
D
B
C
∵边长AB=2cm
∴周长C=4AB=8cm
练习 2、已知:正方形的一条对角线长为4cm
解:∵四边形ABCD是正方形
∴AB = BC,∠ABC=90°
﹙正方形的四个角都是直角,四条边都相等﹚
A
D
B
C
1、正方形的面积等于边长的平方。
2、正方形的面积等于等于对角线的平方的一半。
3、正方形的周长等于边长的4倍。
在Rt⊿ABC中,
求: 它的边长和面积。
练习3、已知:在正方形ABCD中,E、F分别在BC、DC
上,且BE = DF,AC与BC相交于O点,EF
与AC相交于P点
求证:EF ⊥ AC,EF ∥ BD
证明: ∵四边形ABCD是正方形
∴BC = CD
﹙ 正方形的四条边都相等﹚
∵BE = DF
∴EC = FC
∵AC平分∠BCD
﹙ 正方形的每条对角线平分一组对角﹚
∴EF⊥ AC
∵AC ⊥BD
(正方形的对角线互相垂直)
∴ EF ∥ BD
A
B
C
D
O
P
F
E
矩形、正方形(2)
4、判断。
(1)正方形一定是矩形。( )
(2)正方形一定是菱形。( )
(3)菱形一定是正方形。( )
(4)矩形一定是正方形。( )
(5)正方形、矩形、菱形都是平行四边形。( )
快速反应
矩形、正方形(2)
1、在下列性质中,平行四边形具有的是_______,矩形具有的是_________,菱形具有的是_______,正方形具有的是_______________。
(1)四边都相等; (2)对角线互相平分;
(3)对角线相等; (4)对角线互相垂直;
(5)四个角都是直角;
(6)每条对角线平分一组对角;
(7)对边相等且平行;
(8)有两条对称轴。
自主学习
矩形、正方形(2)
2、正方形两条对角线的和为8cm,它的面积为____________.
自主学习
矩形、正方形(2)
3、如图,点E、F在正方形ABCD的边BC、CD上,BE=CF.
(1)AE与BF相等吗?为什么?
(2)AE与BF是否垂直?说明你的理由。
自主学习
尝试练习:
(1)已知:如图,ABCD和AKLM都是正方形,求证:MD=KB。
尝试练习:
(2)如图,正方形ABCD中,AC交BD于O,点M、N分别在AC、BD上,且OM=ON,
求证:BM=CN。
如何设计花坛?
在一块正方形的花坛上,欲修建两条直的小路,使得两条直的小路将花坛平均分成面积相等的四部分(不考虑道路的宽度),你有几种方法?(至少说出三种)
请你当设计师
应用举例:
A
B
C
D
C/
A/
B/
D/
已知:如图点A' 、 B' 、 C'、D'分别是正方形ABCD
四条边上的点,并且AA'=BB'=CC'=DD'
求证:四边形A'B'C'D'是正方形
①、由已知正方形证三角形全等;
②、证得菱形;
③、再证直角;
④、是正方形
证题思路分析
上一页
例1 已知:如图,在正方形ABCD中,A`A=B`B=C`C=D`D 。
求证:四边形A`B`C`D`是正方形。
证明:∵四边形ABCD是正方形 ∴AB=BC=CD=DA
又∵A`A=B`B=C`C=D`D ∴D`A=A`B=B`C=C`D
∵∠A=∠B=∠C=∠D=90° ∴△AA`D`≌△BB`A`≌△CC`B`≌△DD`C`
∴四边形A`B`C`D`是菱形
又∵∠AD`A`=∠BA`B`, ∠ AA`D`+∠AD`A`=90°
∴ ∠AA`D`+∠BA`B`=90 °
∵∠D`A`B`=180°—(∠AA`D`+∠BA`B`)=90°
∴四边形A`B`C`D`是正方形。
例2已知:如图,在矩形ABCD中,AF,BH,CH,DF分别是各内角平分线,AF和BH交于E,CH和DF交于G。 求证:四边形EFGH是正方形
A D
H
B C
F
E
G
证明:∵AD∥BC,AF、BH是角平分线
∴AF⊥BH
同理 BH⊥CH
CH⊥DF DF⊥AF
∴∠HEF=∠EFG=
∠FGH=∠GHE=90°∴四边形EFGH是矩形
A
B
C
D
E
F
G
H
∵AF平分∠BAD ∴∠BAF=∠DAF=45°
同理∠ABH=∠CBH=45°
∠BCH=∠DCH=45°
∠CDF=∠ADF=45°
∵∠DAF=∠CBH
AD=BC
∠ADF=∠BCH
∴△AFD≌△BHC(ASA)
∴AF=BH
∵∠BAF=∠ABH
∴AE=BE
∴EH=EF
∴四边形EFGH是正方形
课堂练习:
1、已知:正方形ABCD中,分别过A、C两点作a∥b,作BM⊥a于M,DN⊥a于N,直线MB、ND分别交b于Q、P。求证:四边形PNMQ是正方形。
2 、已知:如图,正方形ABCD和正方形CEFG,延长CD到H,且DH=CE=BK。求证:四边形AKFH是一个正方形
A
B
C
D
K
F
H
E
G
数学家庭作业:1、课时第65页到67页,
2、五洲导学第46页到47页。
