分式复习课件
图片预览









文档简介
(共33张PPT)
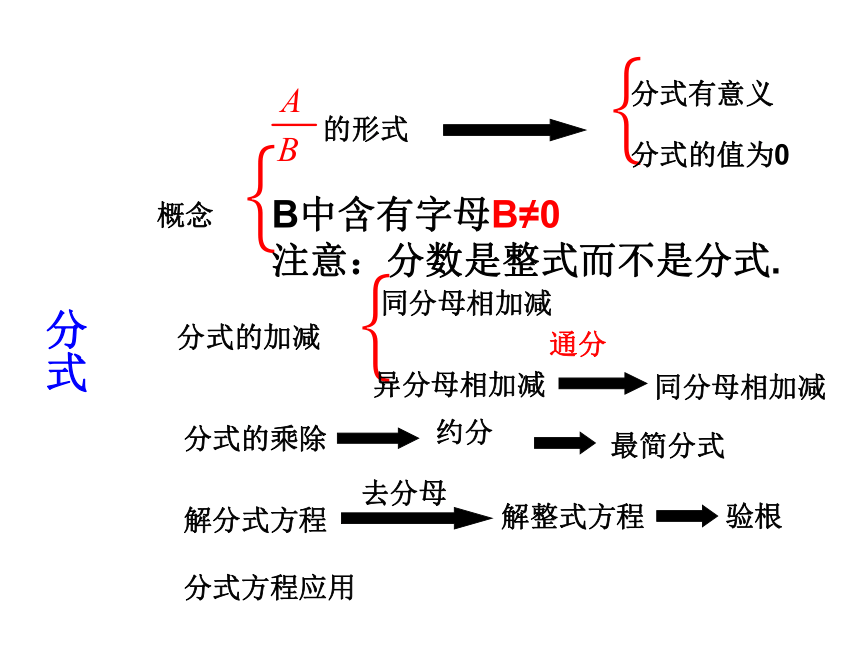
分式
分式有意义
分式的值为0
同分母相加减
异分母相加减
概念
的形式
B中含有字母B≠0
注意:分数是整式而不是分式.
分式的加减
分式的乘除
通分
约分
最简分式
解分式方程
去分母
解整式方程
验根
分式方程应用
同分母相加减
学习目标
1、通过复习进一步熟练掌握分式运算、分式方程的解法及应用。
2、通过复习,了解考试内容及题型。
3、通过复习,提高学生的计算能力及锻炼学生的思维能力,并培养学生的动手动脑习惯。
分式的概念问题
典型例题解析
【例1】 当a取何值时,分式
(1)值为零;(2)分式有意义
解: =
(1)当 时,有
即a=4或a=-1时,分式的值为零.
(2)当2a-3=0即a=3/2时无意义.
故当a≠3/2时,分式有意义.
思考变题:当a为何值时, 的值
(1)为正;(2)为零.
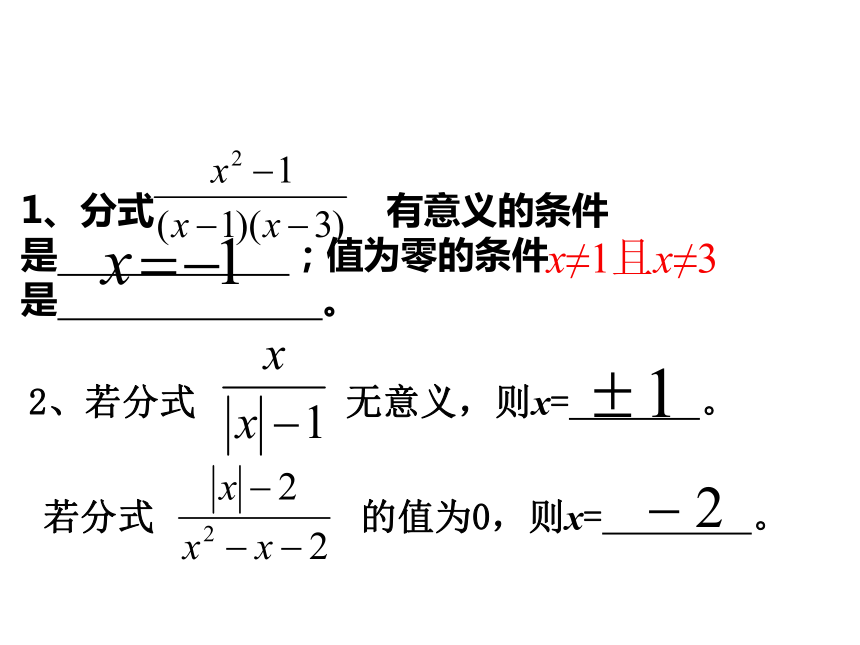
1、分式 有意义的条件是 ;值为零的条件是 。
x≠1且x≠3
2、若分式 无意义,则x= 。
若分式 的值为0,则x= 。
分式的基本性质
分式的符号法则:
分式的分子、分母与分式本身的符号,
改变其中任意两个,分式的值不变.
【例2】 不改变分式的值,先把分式:
的分子、分母的最高次项系数化为正整数,然后约分, 化成最简分式.
解:原式= =
= =
=
=
典型例题解析
1: 若将分式 中的x、y的值都扩大2倍,则分式的值( )
A、扩大2倍 B、不变
C、扩大3倍 D、扩大4倍
A
2:如果把分式
x+2y
x
中的
x
和
y
都扩大
10
倍,那么分式
的值(
)
A
、扩大
10
倍
B
、缩小
10
倍
C
、扩大
2
倍
D
、不变
D
D
课时训练
分式约分的主要步骤是:
1、把分式的分子与分母分解因式。
2、然后约去分子与分母的公因式.
约分一般是将一个分式化为最简分式,将分式约分所得的结果有时可能是整式.
分式的乘法法则:
分式乘以分式,用分子的积做积的分子,分母的积做积的分母.
1、下列等式从左到右的变形一定正确的是( )
2、写出一个分母含有两项且能够约分的分式 。
课时训练
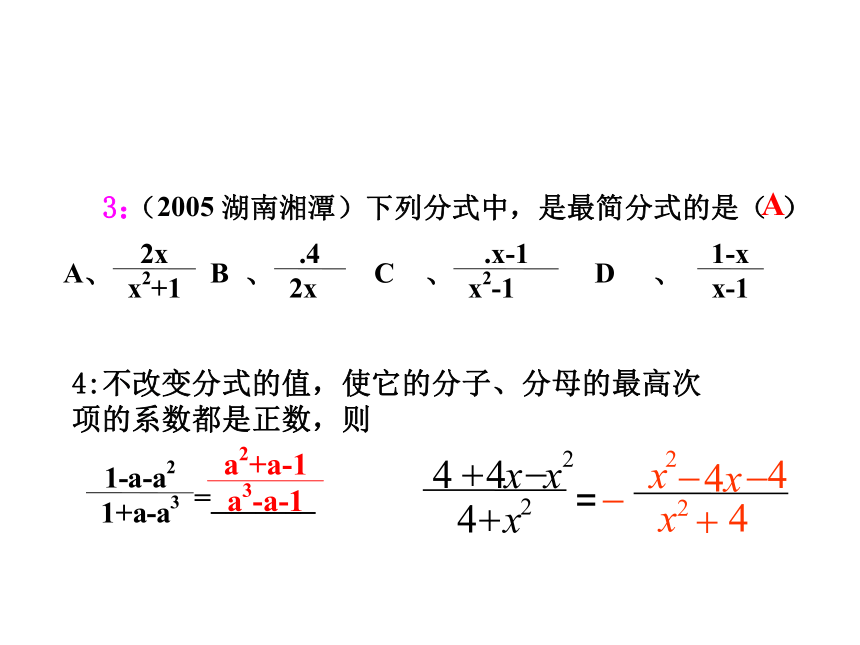
3
:
(
200
5
湖南湘潭)下列分式中,是最简分式的是(
)
A
、
2x
x
2
+1
B
、
.4
2x
C
、
.x
-
1
x
2
-
1
D
、
1
-
x
x
-
1
A
4:不改变分式的值,使它的分子、分母的最高次项的系数都是正数,则
1
-
a
-
a
2
1+a
-
a
3
=_______
2
2
4
4
4
x
x
x
+
-
+
2
2
4
4
4
x
x
x
+
-
-
-
=
分式的运算
【例3】 计算:(1) ;
(2) ;
(3)[( )( )-3]÷( ).
解:(1)原式=
=
=
典型例题解析
【例4】 (2002年·山西省)化简求值:
( ) ÷ ,其中a满足:a2-2a-1=0.
解:原式=[ ]×
= × = ×
= =
典型例题解析
又∵a2+2a-1=0,
∴a2+2a=1
∴原式=1
1.当分式的值为零时,必须同时满足两个条件:
①分子的值为零;
②分母的值不为零.
2.分式的混和运算应注意运算的顺序,同时要
掌握通分、约分等法则,灵活运用分式的基本
性质,注意因式分解、符号变换和运算的技巧,
尤其在通分及变号这两个方面极易出错,要小心
谨慎!
计算或化简
x
x
x
x
-
+
-
-
+
1
1
2
1
1
)
1
(
)
2
(
)
3
(
【例5】(1)已知 求
的值。
(2)已知 求 的值。
典型例题解析
3:若 ( )
A. B. C. D.
(潍坊市)
解:
A
分式方程及应用
分式方程
去分母
整式方程
验根
例 解方程:
解:
两边都乘以
,并整理得;
解得
检验:x=1是原方程的根,x=2是增根
∴原方程的根是x=1
解方程:
无解
注意:检验
列分式方程解应用题的一般步骤
1.审:分析题意,找出研究对象,建立等量关系.
2.设:选择恰当的未知数,注意单位.
3.列:根据等量关系正确列出方程.
4.解:认真仔细.
5.验:有二次检验.
6.答:不要忘记写.
(1)一件工作甲单独做要m小时完成,乙单独做要n小时完成,如果两人合做,完成这
件工作的时间是 小时;
(2)某食堂有米m公斤,原计划每天用粮a公斤,现在每天节约用粮b公斤,则可以比原计划
多用天数是 ;
反馈
解:设江水每小时的流速是x千米,根据题意得:
3.已知轮船在静水中每小时行20千米,如果此船在某江中顺流航行72千米所用的时间与逆流航行48千米所用的时间相同,那么此江水每小时的流速是多少千米
(2004·南宁市)当x 时,分式 有意义。
3.计算: = .
4.在分式① ,② ,③ ,④ 中 ,最
简分式的个数是 ( )
A.1 B.2 C.3 D.4
≠1
2. (2004年·南京)计算: = .
B
1
达标检测
7.(2004年·杭州)甲、乙两人分别从两地同时出发,
若相向而行,则a小时相遇;若同向而行,则b小时
甲追上乙,那么甲的速度是乙速度的 ( )
A. B. C. D.
5 :(2004年·上海)函数 的定义域是 .
6.(2004 年·重庆)若分式 的值为零,则x
的值为 ( )
A.3 B.3或-3 C.-3 D.0
x>-1
C
C
8.若分式 的值为0,则x= 。
10.化简:
-3
9. 已知 则 = .
1/4
2.化简:
3.当1<x<3时,化简 得 ( )
A.1 B.-1 C.3 D.-3
D
1:化简: 的结果是: 。
拓展提高
中考链接 (2002年·山西省)化简求值:
( - ) ÷ ,其中a满足:a2+2a-1=0.
解:原式=[ - ]×
= × = ×
= =
又∵a2+2a-1=0,
∴a2+2a=1
∴原式=1
感悟与收获
这堂课你收获了什么?
达标检测
配练第37页
作业
配练第39页第21、22题
分式
分式有意义
分式的值为0
同分母相加减
异分母相加减
概念
的形式
B中含有字母B≠0
注意:分数是整式而不是分式.
分式的加减
分式的乘除
通分
约分
最简分式
解分式方程
去分母
解整式方程
验根
分式方程应用
同分母相加减
学习目标
1、通过复习进一步熟练掌握分式运算、分式方程的解法及应用。
2、通过复习,了解考试内容及题型。
3、通过复习,提高学生的计算能力及锻炼学生的思维能力,并培养学生的动手动脑习惯。
分式的概念问题
典型例题解析
【例1】 当a取何值时,分式
(1)值为零;(2)分式有意义
解: =
(1)当 时,有
即a=4或a=-1时,分式的值为零.
(2)当2a-3=0即a=3/2时无意义.
故当a≠3/2时,分式有意义.
思考变题:当a为何值时, 的值
(1)为正;(2)为零.
1、分式 有意义的条件是 ;值为零的条件是 。
x≠1且x≠3
2、若分式 无意义,则x= 。
若分式 的值为0,则x= 。
分式的基本性质
分式的符号法则:
分式的分子、分母与分式本身的符号,
改变其中任意两个,分式的值不变.
【例2】 不改变分式的值,先把分式:
的分子、分母的最高次项系数化为正整数,然后约分, 化成最简分式.
解:原式= =
= =
=
=
典型例题解析
1: 若将分式 中的x、y的值都扩大2倍,则分式的值( )
A、扩大2倍 B、不变
C、扩大3倍 D、扩大4倍
A
2:如果把分式
x+2y
x
中的
x
和
y
都扩大
10
倍,那么分式
的值(
)
A
、扩大
10
倍
B
、缩小
10
倍
C
、扩大
2
倍
D
、不变
D
D
课时训练
分式约分的主要步骤是:
1、把分式的分子与分母分解因式。
2、然后约去分子与分母的公因式.
约分一般是将一个分式化为最简分式,将分式约分所得的结果有时可能是整式.
分式的乘法法则:
分式乘以分式,用分子的积做积的分子,分母的积做积的分母.
1、下列等式从左到右的变形一定正确的是( )
2、写出一个分母含有两项且能够约分的分式 。
课时训练
3
:
(
200
5
湖南湘潭)下列分式中,是最简分式的是(
)
A
、
2x
x
2
+1
B
、
.4
2x
C
、
.x
-
1
x
2
-
1
D
、
1
-
x
x
-
1
A
4:不改变分式的值,使它的分子、分母的最高次项的系数都是正数,则
1
-
a
-
a
2
1+a
-
a
3
=_______
2
2
4
4
4
x
x
x
+
-
+
2
2
4
4
4
x
x
x
+
-
-
-
=
分式的运算
【例3】 计算:(1) ;
(2) ;
(3)[( )( )-3]÷( ).
解:(1)原式=
=
=
典型例题解析
【例4】 (2002年·山西省)化简求值:
( ) ÷ ,其中a满足:a2-2a-1=0.
解:原式=[ ]×
= × = ×
= =
典型例题解析
又∵a2+2a-1=0,
∴a2+2a=1
∴原式=1
1.当分式的值为零时,必须同时满足两个条件:
①分子的值为零;
②分母的值不为零.
2.分式的混和运算应注意运算的顺序,同时要
掌握通分、约分等法则,灵活运用分式的基本
性质,注意因式分解、符号变换和运算的技巧,
尤其在通分及变号这两个方面极易出错,要小心
谨慎!
计算或化简
x
x
x
x
-
+
-
-
+
1
1
2
1
1
)
1
(
)
2
(
)
3
(
【例5】(1)已知 求
的值。
(2)已知 求 的值。
典型例题解析
3:若 ( )
A. B. C. D.
(潍坊市)
解:
A
分式方程及应用
分式方程
去分母
整式方程
验根
例 解方程:
解:
两边都乘以
,并整理得;
解得
检验:x=1是原方程的根,x=2是增根
∴原方程的根是x=1
解方程:
无解
注意:检验
列分式方程解应用题的一般步骤
1.审:分析题意,找出研究对象,建立等量关系.
2.设:选择恰当的未知数,注意单位.
3.列:根据等量关系正确列出方程.
4.解:认真仔细.
5.验:有二次检验.
6.答:不要忘记写.
(1)一件工作甲单独做要m小时完成,乙单独做要n小时完成,如果两人合做,完成这
件工作的时间是 小时;
(2)某食堂有米m公斤,原计划每天用粮a公斤,现在每天节约用粮b公斤,则可以比原计划
多用天数是 ;
反馈
解:设江水每小时的流速是x千米,根据题意得:
3.已知轮船在静水中每小时行20千米,如果此船在某江中顺流航行72千米所用的时间与逆流航行48千米所用的时间相同,那么此江水每小时的流速是多少千米
(2004·南宁市)当x 时,分式 有意义。
3.计算: = .
4.在分式① ,② ,③ ,④ 中 ,最
简分式的个数是 ( )
A.1 B.2 C.3 D.4
≠1
2. (2004年·南京)计算: = .
B
1
达标检测
7.(2004年·杭州)甲、乙两人分别从两地同时出发,
若相向而行,则a小时相遇;若同向而行,则b小时
甲追上乙,那么甲的速度是乙速度的 ( )
A. B. C. D.
5 :(2004年·上海)函数 的定义域是 .
6.(2004 年·重庆)若分式 的值为零,则x
的值为 ( )
A.3 B.3或-3 C.-3 D.0
x>-1
C
C
8.若分式 的值为0,则x= 。
10.化简:
-3
9. 已知 则 = .
1/4
2.化简:
3.当1<x<3时,化简 得 ( )
A.1 B.-1 C.3 D.-3
D
1:化简: 的结果是: 。
拓展提高
中考链接 (2002年·山西省)化简求值:
( - ) ÷ ,其中a满足:a2+2a-1=0.
解:原式=[ - ]×
= × = ×
= =
又∵a2+2a-1=0,
∴a2+2a=1
∴原式=1
感悟与收获
这堂课你收获了什么?
达标检测
配练第37页
作业
配练第39页第21、22题
