湖南省岳阳市2020-2021学年高二下学期期末考试数学试题 Word版含答案
文档属性
| 名称 | 湖南省岳阳市2020-2021学年高二下学期期末考试数学试题 Word版含答案 |
|
|
| 格式 | docx | ||
| 文件大小 | 749.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-06 00:00:00 | ||
图片预览





文档简介
岳阳市2021年高二期末教学质量检测试题
数学
本试卷共6页,共22道题,满分150分,考试用时120分钟
注意事项:
1.答卷前,考生务必将自己的姓名、考场号、座位号填写在答题卡上.
2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑.如需改动,用橡皮擦干净后,再选涂其它答案标号,回答非选择题时,将答案写在答题卡上,写在本试卷上无效.
3.考试结束后,将本试卷和答题卡一并交回.
一、单项选择题(本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.已知集合false,false,且满足false,则false( ).
A.false B.0 C.1 D.2
2.已知false,false为第二象限角,则false( ).
A.false B.false C.false D.false
3.“互联网+”时代全民阅读的内涵已多元化,在线读书成为一种生活方式.某高校为了解本校学生阅读情况,拟采用分层抽样方法从该校四个年级中抽取一个容量为360的样本进行调查,大一与大二学生占全校一半,大三学生与大四学生之比为false,则大四学生应抽取的学生为( ).
A.72 B.100 C.108 D.120
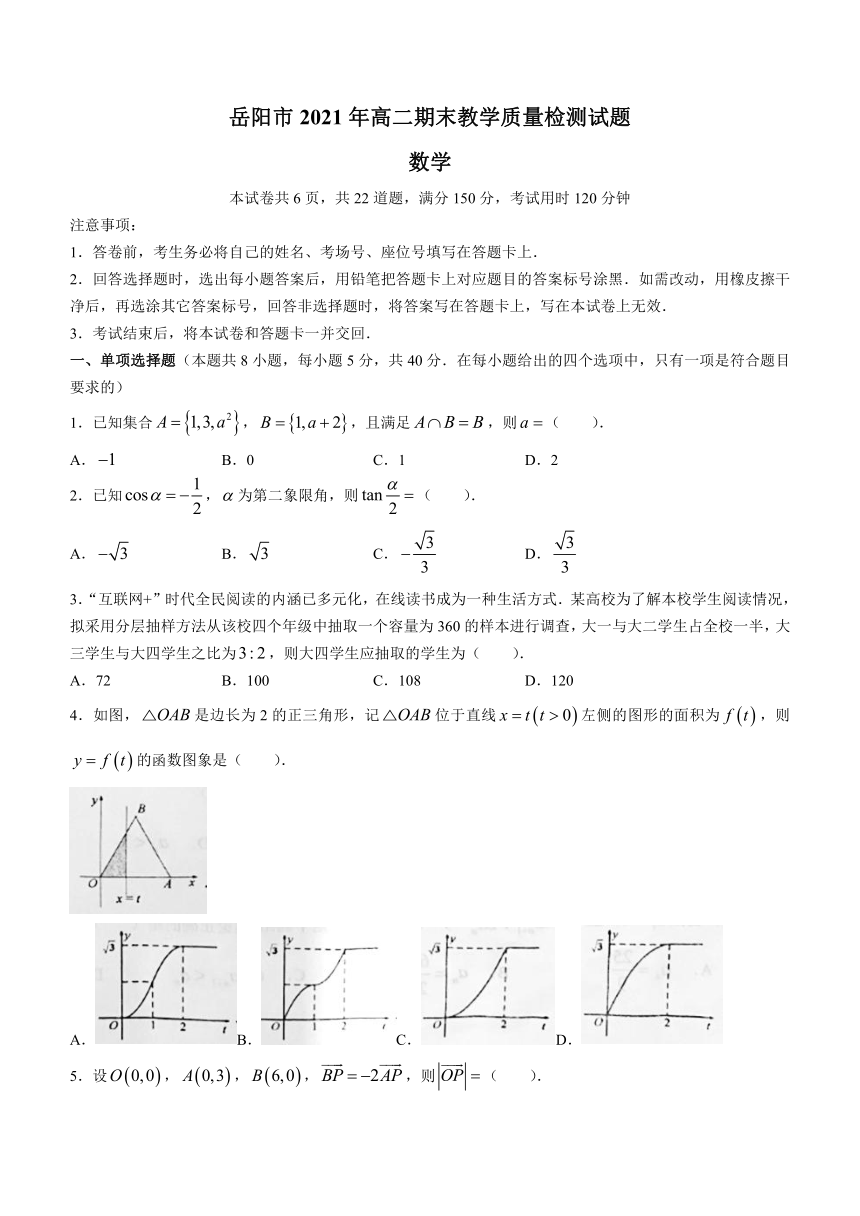
4.如图,false是边长为2的正三角形,记false位于直线false左侧的图形的面积为false,则false的函数图象是( ).
A.B.C.D.
5.设false,false,false,false,则false( ).
A.false B.false C.false D.false
6.当生物体死亡后,它机体内的碳14含量会按确定的比率衰减,大约每经过5730年衰减为原来的一半,这个时间称为“半衰期”.2021年3月23日四川省文物考古研究院联合北京大学对三星堆新发现K4坑的炭屑样品使用碳14年代检测方法进行了分析,发现碳14含量衰减为原来的false%,则该遗址距今约( )年.(参考数据:false)
A.3300 B.3200 C.3100 D.3000
7.已知false,false,false,则
(族法本往,会家技版关.8A.a>c>bB.a>b>cc.c>a>bD.c>b>a8.碳60(Co)是一种非金属单质,它是由60个碳原子构成,形似足球,又称为足球烯,其结构是由五元环(正五边形面)和六元环(正六边形面)组成的封闭的凸多面体,共32个面,且满足:顶点数-棱数+面数=2,则其六元环的个数为( ).
A.12 B.20 C.32 D.60
二、多项选择题(本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,部分选对的得2分,有选错的得0分)
9.在false中,若false,false,false,则false的值可以是( ).
A.false B.false C.false D.false
10.如果一组数据的中位数比平均数小很多,则下面叙述正确的是( ).
A.这组数据是近似对称的 B.数据中可能有极端大的值
C.数据中可能有异常值 D.数据中众数可能和中位数相同
11.已知false,且false,则下列结论正确的是( ).
A.false B.false C.false D.false
12.已知正三棱锥false中,false为false的中点,false,false,则( ).
A.false B. false
C.此正三棱锥的内切球半径为false D.此正三棱锥的外接球表面积false
三、填空题(本题共4小题,每小题5分,共20分)
13.若false为偶函数,则false______.
14.已知false,false,且false,则false的最小值是______.
15.袋子中有5个大小质地完全相同的球,其中2个红球、3个黄球,从中不放回地依次随机摸出2个球,则两次都摸到红球的概率是______.
16.已知false为false的重心,且false,false,则false______,false的最小值为______.
四、解答题(本题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤)
17.(本题满分10分)
已知函数false.
(1)求false的最小正周期以及单调增区间;
(2)在false中,若false,false,求false周长的取值范围.
18.(本题满分12分)
夏天来了,又是一个冷藏饮料销售旺季,某生活小超市据以往统计某天的偏温差false(℃,false)(超出常温度数)和某种饮料的销售量false(瓶)的情况及有关数据如下:
偏温差false℃
false
false
false
false
false
false
销售量false(瓶)
8
11
14
20
23
26
其中false,false,false.
(1)请用相关系数加以说明是否可用线性回归模型拟合销售量false与偏温差false的关系;
(2)建立false关于的回归方程(精确到false),预测当偏温差升高4℃时该种饮料的销售量会有什么变化?(销售量精确到整数)
参考数据:false.
参考公式:相关系数false,
回归直线方程是false,false,false.
19.(本题满分12分)
如图,在三棱柱false中,false,false,false.
(1)证明:平面false平面false;
(2)求四棱锥false的体积.
20.(本题满分12分)
在①false,false,false成等比数列且false,②false,③false,false,false,这三个条件中任选一个,补充到下面问题中,并解答本题.
问题:已知等差数列false的公差为false,前false项和为false,且满足______.
(1)求false;
(2若false的前false项和为false,证明:false .
注:如果选择多种情况分别解答,按第一种解答计分.
21.(本题满分12分)
某企业参加false项目生产的工人为1000人,平均每人每年创造利润10万元.根据现实的需要,从false项目中调出false人参与false项目的售后服务工作,每人每年可以创造利润false万元false,false项目余下的工人每人每年创造利润提高false%.
(1)若要保证false项目余下的工人创造的年总利润不低于原来1000名工人创造的年总利润,则最多调出多少人参加false项目从事售后服务工作?
(2)在(1)的条件下,当从false项目调出的人数不能超过总人数的50%时,才能使得false项目中留岗工人创造的年总利润始终不低于调出的工人所创造的年总利润,求实数false的取值范围.
22.(本题满分12分)
已知动点false与两个定点false,false的距离的比为false,动点false的轨迹为曲线false.
(1)求false的轨迹方程,并说明其形状;
(2)过直线false上的动点false分别作false的两条切线false,false(false、false为切点),false,false交false于点false,
(ⅰ)证明:直线false过定点,并求该定点坐标;
(ⅱ)是否存在点false,使false的面积最大?若存在,求出点false坐标:若不存在,请说明理由.
岳阳市2021年高二期末教学质量检测
数学参考答案及评分细则
一、单项选择题(本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的)
题号
1
2
3
4
5
6
7
8
答案
D
B
A
A
B
C
D
B
二、多项选择题(本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,部分选对的得2分,有选错的得0分)
题号
9
10
11
12
答案
CD
BCD
BD
ABC
三、填空题(本题共4小题,每小题5分,共20分)
13.0 14.8 15false 16.4,false
四、解答题(本题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤)
17.(本题满分10分)
【解答】(1)false
false
false
所以false的最小正周期为false.
单调增区间由false,false,
解得false,false.
(2)false,false,所以false,
由正弦定理false,false,
所以false,false,false,
false
false
因为false,所以false,false,
所以false周长false.
18.(本题满分12分)
【解答】(1)false,false,
又false,false,false.
故false,
∴可用线性回归模型拟合false与false的关系.
(2)false,false,
false,
∴false关于false的回归方程为false.
当false时,false.
预测当偏温差升高4℃时该种饮料的销售量会增加10瓶.
19.(本题满分12分)
【解答】(1)如图,作false的中点false,连false,false,
因为false,false,
所以false,false,
又因为false,所以false,
在false中,由false,满足false,
所以false,且false,false,
所以false平面false,
又false平面false,所以平面false平面false,
又平面false平面false,所以平面false平面false.
(2)由(1)可知false平面false,
四棱锥false的体积false.
20.(本题满分12分)
【解答】(1)选择条件①
由false,得false,即false,
由false,false,false成等比数列,得false,
即false,即false,
解得false,false,因此false.
选择条件②
由false得,false,
两式相减,并整理得:false,false,
又false,所以false,
所以false,即false.
令false,false,解得false,故false.
选择条件③
等差数列false的前false项和false,故false,
所以false为等差数列,
于是false,即false,解得false,
故false,false,false,解得基本量false,false,
因此false.
(2)由false,false或得false,
false,
所以false.
21.(本题满分12分)
【解答】设调出false人参加false项目从事售后服务工作.
(1)由题意得false,
即false,
又false,所以false.
即最多调出500名员工从事第三产业.
(2)由题知,false,
从事第三产业的员工创造的年总利润为false万元,
从事原来产业的员工的年总利润为false万元,
则false,
所以false,
所以false,即false恒成立,
因为false,所以false,
所以false,
又false,所以false,即false的取值范围为false.
22.(本题满分12分)
【解答】(1)设false,由false,得false.
化简得false,即false.
故曲线false是以false,0为圆心,半径为2的圆.
(2)(ⅰ)证明方法一(由两圆相交弦方程求切点弦方程):
由题意知,false、false与圆相切,false、false为切点,
则false,false,
则false、false、false、false四点共圆,false、false在以false为直径的圆上(如图).
设false,又false,
则false的中点为false,false.
以线段false为直径的圆的方程为false,
整理得false, ①
(也可用圆的直径式方程false化简得.)
又false、false在false上, ②
由两圆方程作差即②-①得:false.
所以,切点弦false所在直线的方程为false.
则false恒过坐标原点false.
证明方法二(求false、false均满足的同一直线方程即切点弦方程):
设false,false,false.
由false,可得false处的切线上任一点false满足false(如图),
即切线false方程为false.
整理得false.
又false,
整理得false.
同理,可得false处的切线false方程为false.
又false既在切线false上,又在切线false上,
所以false,整理得false.
显然,false,false的坐标都满足直线false的方程.
而两点确定一条直线,所以切点弦false所在直线的方程为false的方程.
则false恒过坐标原点false.
(ⅱ)false,
因为false,所以点false在以false为直径的圆周上,
故false,即false,此时false,
又由点false,false,false三点共线,所以false,false,
所以false,即false.
数学
本试卷共6页,共22道题,满分150分,考试用时120分钟
注意事项:
1.答卷前,考生务必将自己的姓名、考场号、座位号填写在答题卡上.
2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑.如需改动,用橡皮擦干净后,再选涂其它答案标号,回答非选择题时,将答案写在答题卡上,写在本试卷上无效.
3.考试结束后,将本试卷和答题卡一并交回.
一、单项选择题(本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.已知集合false,false,且满足false,则false( ).
A.false B.0 C.1 D.2
2.已知false,false为第二象限角,则false( ).
A.false B.false C.false D.false
3.“互联网+”时代全民阅读的内涵已多元化,在线读书成为一种生活方式.某高校为了解本校学生阅读情况,拟采用分层抽样方法从该校四个年级中抽取一个容量为360的样本进行调查,大一与大二学生占全校一半,大三学生与大四学生之比为false,则大四学生应抽取的学生为( ).
A.72 B.100 C.108 D.120
4.如图,false是边长为2的正三角形,记false位于直线false左侧的图形的面积为false,则false的函数图象是( ).
A.B.C.D.
5.设false,false,false,false,则false( ).
A.false B.false C.false D.false
6.当生物体死亡后,它机体内的碳14含量会按确定的比率衰减,大约每经过5730年衰减为原来的一半,这个时间称为“半衰期”.2021年3月23日四川省文物考古研究院联合北京大学对三星堆新发现K4坑的炭屑样品使用碳14年代检测方法进行了分析,发现碳14含量衰减为原来的false%,则该遗址距今约( )年.(参考数据:false)
A.3300 B.3200 C.3100 D.3000
7.已知false,false,false,则
(族法本往,会家技版关.8A.a>c>bB.a>b>cc.c>a>bD.c>b>a8.碳60(Co)是一种非金属单质,它是由60个碳原子构成,形似足球,又称为足球烯,其结构是由五元环(正五边形面)和六元环(正六边形面)组成的封闭的凸多面体,共32个面,且满足:顶点数-棱数+面数=2,则其六元环的个数为( ).
A.12 B.20 C.32 D.60
二、多项选择题(本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,部分选对的得2分,有选错的得0分)
9.在false中,若false,false,false,则false的值可以是( ).
A.false B.false C.false D.false
10.如果一组数据的中位数比平均数小很多,则下面叙述正确的是( ).
A.这组数据是近似对称的 B.数据中可能有极端大的值
C.数据中可能有异常值 D.数据中众数可能和中位数相同
11.已知false,且false,则下列结论正确的是( ).
A.false B.false C.false D.false
12.已知正三棱锥false中,false为false的中点,false,false,则( ).
A.false B. false
C.此正三棱锥的内切球半径为false D.此正三棱锥的外接球表面积false
三、填空题(本题共4小题,每小题5分,共20分)
13.若false为偶函数,则false______.
14.已知false,false,且false,则false的最小值是______.
15.袋子中有5个大小质地完全相同的球,其中2个红球、3个黄球,从中不放回地依次随机摸出2个球,则两次都摸到红球的概率是______.
16.已知false为false的重心,且false,false,则false______,false的最小值为______.
四、解答题(本题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤)
17.(本题满分10分)
已知函数false.
(1)求false的最小正周期以及单调增区间;
(2)在false中,若false,false,求false周长的取值范围.
18.(本题满分12分)
夏天来了,又是一个冷藏饮料销售旺季,某生活小超市据以往统计某天的偏温差false(℃,false)(超出常温度数)和某种饮料的销售量false(瓶)的情况及有关数据如下:
偏温差false℃
false
false
false
false
false
false
销售量false(瓶)
8
11
14
20
23
26
其中false,false,false.
(1)请用相关系数加以说明是否可用线性回归模型拟合销售量false与偏温差false的关系;
(2)建立false关于的回归方程(精确到false),预测当偏温差升高4℃时该种饮料的销售量会有什么变化?(销售量精确到整数)
参考数据:false.
参考公式:相关系数false,
回归直线方程是false,false,false.
19.(本题满分12分)
如图,在三棱柱false中,false,false,false.
(1)证明:平面false平面false;
(2)求四棱锥false的体积.
20.(本题满分12分)
在①false,false,false成等比数列且false,②false,③false,false,false,这三个条件中任选一个,补充到下面问题中,并解答本题.
问题:已知等差数列false的公差为false,前false项和为false,且满足______.
(1)求false;
(2若false的前false项和为false,证明:false .
注:如果选择多种情况分别解答,按第一种解答计分.
21.(本题满分12分)
某企业参加false项目生产的工人为1000人,平均每人每年创造利润10万元.根据现实的需要,从false项目中调出false人参与false项目的售后服务工作,每人每年可以创造利润false万元false,false项目余下的工人每人每年创造利润提高false%.
(1)若要保证false项目余下的工人创造的年总利润不低于原来1000名工人创造的年总利润,则最多调出多少人参加false项目从事售后服务工作?
(2)在(1)的条件下,当从false项目调出的人数不能超过总人数的50%时,才能使得false项目中留岗工人创造的年总利润始终不低于调出的工人所创造的年总利润,求实数false的取值范围.
22.(本题满分12分)
已知动点false与两个定点false,false的距离的比为false,动点false的轨迹为曲线false.
(1)求false的轨迹方程,并说明其形状;
(2)过直线false上的动点false分别作false的两条切线false,false(false、false为切点),false,false交false于点false,
(ⅰ)证明:直线false过定点,并求该定点坐标;
(ⅱ)是否存在点false,使false的面积最大?若存在,求出点false坐标:若不存在,请说明理由.
岳阳市2021年高二期末教学质量检测
数学参考答案及评分细则
一、单项选择题(本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的)
题号
1
2
3
4
5
6
7
8
答案
D
B
A
A
B
C
D
B
二、多项选择题(本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,部分选对的得2分,有选错的得0分)
题号
9
10
11
12
答案
CD
BCD
BD
ABC
三、填空题(本题共4小题,每小题5分,共20分)
13.0 14.8 15false 16.4,false
四、解答题(本题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤)
17.(本题满分10分)
【解答】(1)false
false
false
所以false的最小正周期为false.
单调增区间由false,false,
解得false,false.
(2)false,false,所以false,
由正弦定理false,false,
所以false,false,false,
false
false
因为false,所以false,false,
所以false周长false.
18.(本题满分12分)
【解答】(1)false,false,
又false,false,false.
故false,
∴可用线性回归模型拟合false与false的关系.
(2)false,false,
false,
∴false关于false的回归方程为false.
当false时,false.
预测当偏温差升高4℃时该种饮料的销售量会增加10瓶.
19.(本题满分12分)
【解答】(1)如图,作false的中点false,连false,false,
因为false,false,
所以false,false,
又因为false,所以false,
在false中,由false,满足false,
所以false,且false,false,
所以false平面false,
又false平面false,所以平面false平面false,
又平面false平面false,所以平面false平面false.
(2)由(1)可知false平面false,
四棱锥false的体积false.
20.(本题满分12分)
【解答】(1)选择条件①
由false,得false,即false,
由false,false,false成等比数列,得false,
即false,即false,
解得false,false,因此false.
选择条件②
由false得,false,
两式相减,并整理得:false,false,
又false,所以false,
所以false,即false.
令false,false,解得false,故false.
选择条件③
等差数列false的前false项和false,故false,
所以false为等差数列,
于是false,即false,解得false,
故false,false,false,解得基本量false,false,
因此false.
(2)由false,false或得false,
false,
所以false.
21.(本题满分12分)
【解答】设调出false人参加false项目从事售后服务工作.
(1)由题意得false,
即false,
又false,所以false.
即最多调出500名员工从事第三产业.
(2)由题知,false,
从事第三产业的员工创造的年总利润为false万元,
从事原来产业的员工的年总利润为false万元,
则false,
所以false,
所以false,即false恒成立,
因为false,所以false,
所以false,
又false,所以false,即false的取值范围为false.
22.(本题满分12分)
【解答】(1)设false,由false,得false.
化简得false,即false.
故曲线false是以false,0为圆心,半径为2的圆.
(2)(ⅰ)证明方法一(由两圆相交弦方程求切点弦方程):
由题意知,false、false与圆相切,false、false为切点,
则false,false,
则false、false、false、false四点共圆,false、false在以false为直径的圆上(如图).
设false,又false,
则false的中点为false,false.
以线段false为直径的圆的方程为false,
整理得false, ①
(也可用圆的直径式方程false化简得.)
又false、false在false上, ②
由两圆方程作差即②-①得:false.
所以,切点弦false所在直线的方程为false.
则false恒过坐标原点false.
证明方法二(求false、false均满足的同一直线方程即切点弦方程):
设false,false,false.
由false,可得false处的切线上任一点false满足false(如图),
即切线false方程为false.
整理得false.
又false,
整理得false.
同理,可得false处的切线false方程为false.
又false既在切线false上,又在切线false上,
所以false,整理得false.
显然,false,false的坐标都满足直线false的方程.
而两点确定一条直线,所以切点弦false所在直线的方程为false的方程.
则false恒过坐标原点false.
(ⅱ)false,
因为false,所以点false在以false为直径的圆周上,
故false,即false,此时false,
又由点false,false,false三点共线,所以false,false,
所以false,即false.
同课章节目录
