北京市朝阳区2020-2021学年高二下学期期末考试数学试题 Word版含答案
文档属性
| 名称 | 北京市朝阳区2020-2021学年高二下学期期末考试数学试题 Word版含答案 |  | |
| 格式 | docx | ||
| 文件大小 | 578.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-06 10:35:16 | ||
图片预览




文档简介
北京市朝阳区2020-2021学年度第二学期期末质量检测
高二年级数学试卷 2021.7
(考试时间120分钟 满分150分)
本试卷分为选择题(共50分)和非选择题(共100分)两部分
第一部分(选择题 共50分)
一、选择题:本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,选出符合题目要求的一项.
1.设false,则“false”是“false”的
A.充分不必要条件 B. 必要不充分条件
C.充要条件 D. 既不充分也不必要条件
2.falsefalsefalse展开式中false的系数为
A. false20 B. false10 C. 10 D. 20
3.函数false在区间false上的最大值为
A.false B.false C.false D.false
4.袋子里有8个红球和4个黄球,从袋子里有放回地随机抽取4个球,用false表示取到红球的个数,则false
A.false B. false C. false D. false
5.设随机变量false服从正态分布false,若false,false,则false
A.1 B. 2 C. 3 D. 4
6.从4名高一学生和5名高二学生中,选3人参加社区垃圾分类宣传活动,其中至少有1名高二学生参加宣传活动的不同选法种数为
A. false B. false C. false D. false
7.小王同学进行投篮练习,若他第1球投进,则第2球投进的概率为false;若他第1球投不进,则第2球投进的概率为false.若他第1球投进的概率为false,则他第2球投进的概率为
A. false B. false C. false D. false
8.为了研究某校男生的脚长false00(单位:false)和身高false00(单位:false)的关系,从该校随机抽取false名男生,根据测量数据的散点图可以看出false00与false00之间有线性相关关系.设false关于false的经验回归方程为false00.已知false00,false00,false00,该校某男生的脚长为falsefalse,据此估计其身高为
A.00false false 00 B.00false false C.false false00 D.false false00
9.已知falsefalse.以下四个命题:
①对任意实数false,存在false,使得false;
②对任意false,存在实数false,使得false;
③对任意实数false,false,均有false成立;
④对任意实数false,false,均有false成立.
其中所有正确的命题是
A. ①②00 00B. ②③00 C. ①③ 00 D. ②④ 00
10.一个圆的圆周上有8个点,连接任意两点画出弦.如果有一对弦不相交且没有共同的端点,我们称它们为一组“自由弦对”.则此圆上的“自由弦对”总组数为
A.70 B. 140 C. 210 D. 280
二、填空题:本大题共6小题,每小题5分,共30分.把答案填在答题卡上.
11.判断对错,并在相应横线处划“√”或“×”.
①样本相关系数false时,称成对数据正相关,false时,称成对数据负相关________;
②样本相关系数的绝对值false越接近于1,线性相关程度越弱,false越接近于0,线性相关程度越强________.
12.已知false,则false的最小值为______.
13.某单位工会组织75名会员观看《光荣与梦想》、《觉醒年代》、《跨过鸭绿江》三部建党百年优秀电视剧,对这三部剧的观看情况统计如下:
观看情况
观看人数
只看过《光荣与梦想》
12
只看过《觉醒年代》
11
只看过《跨过鸭绿江》
8
只看过《光荣与梦想》和《觉醒年代》
7
只看过《光荣与梦想》和《跨过鸭绿江》
4
只看过《觉醒年代》和《跨过鸭绿江》
5
同时看过《光荣与梦想》、《觉醒年代》和《跨过鸭绿江》
21
则会员中看过《跨过鸭绿江》的共有 人,三部电视剧中,看过至少一部的有 人.
14. 为了唤起全民对睡眠重要性的认识,国际精神卫生组织于2001年发起了一项全球性的活动——将每年的3月21日定为“世界睡眠日”.现从某中学初一至高三学生中随机抽取部分学生进行睡眠质量调查,采用睡眠质量指数量表统计结果如下:
性别
人数
睡眠质量好
睡眠质量一般
睡眠质量差
男
220
99
90
31
女
250
50
120
80
合计
470
149
210
111
假设所有学生睡眠质量的程度是相互独立的.以调查结果的频率估计概率,现从该中学男生和女生中各随机抽取1人,二人中恰有一人睡眠质量好的概率是 .
2640330110045515.我国南宋数学家杨辉在1261年所著的《详解九章算法》里,出现了图1这张表.杨辉三角的发现比欧洲早500年左右.如图2,杨辉三角的第false行的各数就是false的展开式的二项式系数.
109220145415
图1 图2
则第10行共有_________个奇数;第100行共有_________个奇数.
16.函数false的定义域为________,极大值点的集合为________.
三、解答题:本大题共5小题,共70分.解答应写出文字说明,演算步骤或证明过程.
17.(本小题满分13分)
已知集合false,false.
(Ⅰ)若false,全集false,求false;
(Ⅱ) 从条件①和条件②选择一个作为已知,求实数false的取值范围.
条件①: 若false;
条件②: 若false.
如果选择条件①、条件②分别解答,则按第一个解答计分.
18.(本小题满分13分)
设函数false,false,false.
(Ⅰ)求false的单调递增区间;
(Ⅱ)当false,false时,求证:false
19.(本小题满分14分)
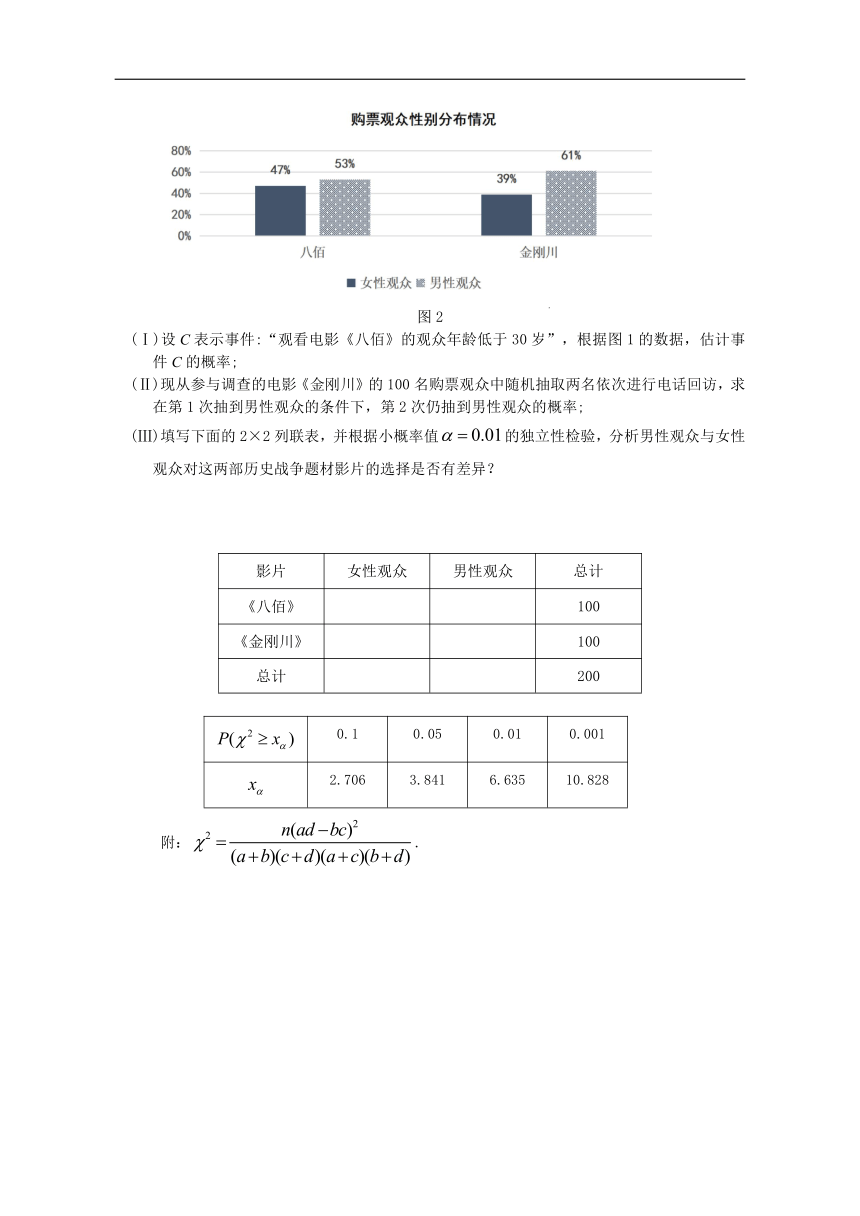
根据国家电影局发布的数据,2020年中国电影总票房为204.17亿,年度票房首度超越北美,成为2020年全球第一大电影市场.国产历史战争题材影片《八佰》和《金刚川》合力贡献了国内全年票房的false.我们用简单随机抽样的方法,分别从这两部电影的购票观众中各随机调查了100名观众,得到结果如下:图1是购票观众年龄分布情况;图2是购票观众性别分布情况.
图1
图2
(Ⅰ)设C表示事件:“观看电影《八佰》的观众年龄低于30岁”,根据图1的数据,估计事件C的概率;
(Ⅱ)现从参与调查的电影《金刚川》的100名购票观众中随机抽取两名依次进行电话回访,求在第1次抽到男性观众的条件下,第2次仍抽到男性观众的概率;
(Ⅲ)填写下面的2×2列联表,并根据小概率值false的独立性检验,分析男性观众与女性观众对这两部历史战争题材影片的选择是否有差异?
影片
女性观众
男性观众
总计
《八佰》
100
《金刚川》
100
总计
200
false
0.1
0.05
0.01
0.001
false
2.706
3.841
6.635
10.828
附:false.
20. (本小题满分15分)
某工厂生产的10件产品中,有8件优等产品,2件不合格产品.
(Ⅰ)若从这10件产品中不放回地抽取两次,每次随机抽取一件,求第二次取出的是不合格产品的概率;
(Ⅱ)若从这10件产品中随机抽取3件,设抽到的不合格产品件数为false,求false的分布列和数学期望;
(Ⅲ)某工作人员在不知情的情况下,从这10件产品中随机抽取了3件产品销售给了下级经销商.现该工厂针对3件已销售产品中可能出现的不合格产品,提出以下两种处理方案:
方案一 将不合格产品返厂再加工,不合格产品的再加工费用为每件200元,所有返厂产品的运输费用为一次性80元;
方案二 将不合格产品就地销毁,每件不合格产品损失成本300元.
若以返厂再加工费用与运输费用之和的期望值为决策依据,要使损失最小,应选择哪种方案处理不合
产品?
21.(本小题满分15分)
已知函数false
(Ⅰ)求false的极值;
(Ⅱ)已知false,且falsefalse对任意的false恒成立,求false的最大值;
(Ⅲ)设false的零点为falsefalse,当false,且false时,
证明:false
北京市朝阳区2020-2021学年度第二学期期末质量检测
高二年级数学试卷答案 2021.7
一、选择题:(本题满分50分)
题号
1
2
3
4
5
6
7
8
9
10
答案
B
C
D
B
C
C
A
C
A
B
二、填空题:(本题满分30分)
题号
11
12
13
14
15
16
答案
√×
false
38
68
false
4
8
false
false
三、解答题:(本题满分70分)
17.(本小题满分13分)
解:(Ⅰ)由false,得false.
所以false.
当false时,可求得false.
所以false,
false …………………………………………………7分
(Ⅱ)若选择条件①:
由false,得false.则false,解得false.
则false的取值范围false. …………………………………………………13分
若选择条件②:
因为false,false,
又false,所以false或false.
解得false或false.
则false的取值范围false或false. ……………………………………13分
18. (本小题满分13分)
解:(Ⅰ)false,falsefalse.
当false时,因为false,所以false恒成立,故false的单调递增区间为false;
当false时,令false,解得false,故当false时,false;
当false时,false,故false的单调递增区间为false
综合以上,当false时,false的单调递增区间为false;当false时,false的单调递增区间为false. …………………………………..7分
(Ⅱ) 设false,则false,false
由(Ⅰ)知,当false时,false在false上单调递增,即false当且仅当false 时等号成立.
故false 因false,故false,
所以false
所以false在区间false上单调递增,且false,所以当false时,false即
false. …………………………………..13分
19.(本小题满分14分)
解:
(Ⅰ) false
则估计观看电影《八佰》的观众年龄低于30岁的概率为0.57. …………………………..4分
(Ⅱ)设事件false为“第1次抽到男性观众”,事件false为“第2次抽到男性观众”.
已知第1次抽到男性观众,这时还剩下99人,其中女性观众39人,男性观众60人.因此,事件false发生的条件下,事件false发生的概率为
false. …………………………..8分(Ⅲ)零假设为
false:影片与观众性别独立,即男性和女性观众对这两部历史战争题材影片的选择没有差异.
影片
女性观众
男性观众
总计
《八佰》
47
53
100
《金刚川》
39
61
100
总计
86
114
200
根据false列联表中的数据可得
false false
根据小概率值false的独立性检验,没有充分证据推断false不成立,因此可以认为false成立,即认为男女观众对这两部历史战争题材影片的选择没有差异. ………………..14分
20.(本小题满分15分)
解:(Ⅰ)设false表示事件“第false次抽到的是优等产品”,因为是不放回抽样,所以:
false
所以falsefalse. ………………………..5分
(Ⅱ) false=0,1,2
false,false,false
false
0
1
2
false
false
false
false
false. ………………………..11分
(Ⅲ)设方案一产生的费用为false,
则false ,
false
0
1
2
false
0
280
480
false
false
false
false
false元.
设方案二产生的费用为false,
则false,false元.
由于false,故应该将不合格产品返厂再加工.
因此应选择方案一. ……………………..15分
21. (本小题满分15分)
解:(Ⅰ)因false,令false,解得false,
当false变化时,false的变化情况如下表:
false
false
1
false
false
false
0
false
false
单调递减
极小值false
单调递增
当false时,函数false取极小值false,无极大值. ……………………..5分
(Ⅱ)设false的较大零点为false,由(Ⅰ)知false在区间false上单调递增,且false,false,故false,则当false时,false,当false时,false.
当false时,false恒成立,即false恒成立.设false,则false,显然false与false同号,所以,false在false上单调递减,在false上单调递增,falsefalse,则false,又因false,所以false的最大值为3. ……………………..10分
(Ⅲ)因false,false
false,
当false时,false,false单调递增.
而false,false,
则方程false在false上有唯一实数根,即false
则false
要证:当false时,false,即证false.
设false,
则只需证明false在区间false上单调递增.
因false,
根据函数单调性容易判定false在false上单调递增,且false,故false,所以,false在false上单调递增,因false,则false.所以当false时,false. ……………………..15分
高二年级数学试卷 2021.7
(考试时间120分钟 满分150分)
本试卷分为选择题(共50分)和非选择题(共100分)两部分
第一部分(选择题 共50分)
一、选择题:本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,选出符合题目要求的一项.
1.设false,则“false”是“false”的
A.充分不必要条件 B. 必要不充分条件
C.充要条件 D. 既不充分也不必要条件
2.falsefalsefalse展开式中false的系数为
A. false20 B. false10 C. 10 D. 20
3.函数false在区间false上的最大值为
A.false B.false C.false D.false
4.袋子里有8个红球和4个黄球,从袋子里有放回地随机抽取4个球,用false表示取到红球的个数,则false
A.false B. false C. false D. false
5.设随机变量false服从正态分布false,若false,false,则false
A.1 B. 2 C. 3 D. 4
6.从4名高一学生和5名高二学生中,选3人参加社区垃圾分类宣传活动,其中至少有1名高二学生参加宣传活动的不同选法种数为
A. false B. false C. false D. false
7.小王同学进行投篮练习,若他第1球投进,则第2球投进的概率为false;若他第1球投不进,则第2球投进的概率为false.若他第1球投进的概率为false,则他第2球投进的概率为
A. false B. false C. false D. false
8.为了研究某校男生的脚长false00(单位:false)和身高false00(单位:false)的关系,从该校随机抽取false名男生,根据测量数据的散点图可以看出false00与false00之间有线性相关关系.设false关于false的经验回归方程为false00.已知false00,false00,false00,该校某男生的脚长为falsefalse,据此估计其身高为
A.00false false 00 B.00false false C.false false00 D.false false00
9.已知falsefalse.以下四个命题:
①对任意实数false,存在false,使得false;
②对任意false,存在实数false,使得false;
③对任意实数false,false,均有false成立;
④对任意实数false,false,均有false成立.
其中所有正确的命题是
A. ①②00 00B. ②③00 C. ①③ 00 D. ②④ 00
10.一个圆的圆周上有8个点,连接任意两点画出弦.如果有一对弦不相交且没有共同的端点,我们称它们为一组“自由弦对”.则此圆上的“自由弦对”总组数为
A.70 B. 140 C. 210 D. 280
二、填空题:本大题共6小题,每小题5分,共30分.把答案填在答题卡上.
11.判断对错,并在相应横线处划“√”或“×”.
①样本相关系数false时,称成对数据正相关,false时,称成对数据负相关________;
②样本相关系数的绝对值false越接近于1,线性相关程度越弱,false越接近于0,线性相关程度越强________.
12.已知false,则false的最小值为______.
13.某单位工会组织75名会员观看《光荣与梦想》、《觉醒年代》、《跨过鸭绿江》三部建党百年优秀电视剧,对这三部剧的观看情况统计如下:
观看情况
观看人数
只看过《光荣与梦想》
12
只看过《觉醒年代》
11
只看过《跨过鸭绿江》
8
只看过《光荣与梦想》和《觉醒年代》
7
只看过《光荣与梦想》和《跨过鸭绿江》
4
只看过《觉醒年代》和《跨过鸭绿江》
5
同时看过《光荣与梦想》、《觉醒年代》和《跨过鸭绿江》
21
则会员中看过《跨过鸭绿江》的共有 人,三部电视剧中,看过至少一部的有 人.
14. 为了唤起全民对睡眠重要性的认识,国际精神卫生组织于2001年发起了一项全球性的活动——将每年的3月21日定为“世界睡眠日”.现从某中学初一至高三学生中随机抽取部分学生进行睡眠质量调查,采用睡眠质量指数量表统计结果如下:
性别
人数
睡眠质量好
睡眠质量一般
睡眠质量差
男
220
99
90
31
女
250
50
120
80
合计
470
149
210
111
假设所有学生睡眠质量的程度是相互独立的.以调查结果的频率估计概率,现从该中学男生和女生中各随机抽取1人,二人中恰有一人睡眠质量好的概率是 .
2640330110045515.我国南宋数学家杨辉在1261年所著的《详解九章算法》里,出现了图1这张表.杨辉三角的发现比欧洲早500年左右.如图2,杨辉三角的第false行的各数就是false的展开式的二项式系数.
109220145415
图1 图2
则第10行共有_________个奇数;第100行共有_________个奇数.
16.函数false的定义域为________,极大值点的集合为________.
三、解答题:本大题共5小题,共70分.解答应写出文字说明,演算步骤或证明过程.
17.(本小题满分13分)
已知集合false,false.
(Ⅰ)若false,全集false,求false;
(Ⅱ) 从条件①和条件②选择一个作为已知,求实数false的取值范围.
条件①: 若false;
条件②: 若false.
如果选择条件①、条件②分别解答,则按第一个解答计分.
18.(本小题满分13分)
设函数false,false,false.
(Ⅰ)求false的单调递增区间;
(Ⅱ)当false,false时,求证:false
19.(本小题满分14分)
根据国家电影局发布的数据,2020年中国电影总票房为204.17亿,年度票房首度超越北美,成为2020年全球第一大电影市场.国产历史战争题材影片《八佰》和《金刚川》合力贡献了国内全年票房的false.我们用简单随机抽样的方法,分别从这两部电影的购票观众中各随机调查了100名观众,得到结果如下:图1是购票观众年龄分布情况;图2是购票观众性别分布情况.
图1
图2
(Ⅰ)设C表示事件:“观看电影《八佰》的观众年龄低于30岁”,根据图1的数据,估计事件C的概率;
(Ⅱ)现从参与调查的电影《金刚川》的100名购票观众中随机抽取两名依次进行电话回访,求在第1次抽到男性观众的条件下,第2次仍抽到男性观众的概率;
(Ⅲ)填写下面的2×2列联表,并根据小概率值false的独立性检验,分析男性观众与女性观众对这两部历史战争题材影片的选择是否有差异?
影片
女性观众
男性观众
总计
《八佰》
100
《金刚川》
100
总计
200
false
0.1
0.05
0.01
0.001
false
2.706
3.841
6.635
10.828
附:false.
20. (本小题满分15分)
某工厂生产的10件产品中,有8件优等产品,2件不合格产品.
(Ⅰ)若从这10件产品中不放回地抽取两次,每次随机抽取一件,求第二次取出的是不合格产品的概率;
(Ⅱ)若从这10件产品中随机抽取3件,设抽到的不合格产品件数为false,求false的分布列和数学期望;
(Ⅲ)某工作人员在不知情的情况下,从这10件产品中随机抽取了3件产品销售给了下级经销商.现该工厂针对3件已销售产品中可能出现的不合格产品,提出以下两种处理方案:
方案一 将不合格产品返厂再加工,不合格产品的再加工费用为每件200元,所有返厂产品的运输费用为一次性80元;
方案二 将不合格产品就地销毁,每件不合格产品损失成本300元.
若以返厂再加工费用与运输费用之和的期望值为决策依据,要使损失最小,应选择哪种方案处理不合
产品?
21.(本小题满分15分)
已知函数false
(Ⅰ)求false的极值;
(Ⅱ)已知false,且falsefalse对任意的false恒成立,求false的最大值;
(Ⅲ)设false的零点为falsefalse,当false,且false时,
证明:false
北京市朝阳区2020-2021学年度第二学期期末质量检测
高二年级数学试卷答案 2021.7
一、选择题:(本题满分50分)
题号
1
2
3
4
5
6
7
8
9
10
答案
B
C
D
B
C
C
A
C
A
B
二、填空题:(本题满分30分)
题号
11
12
13
14
15
16
答案
√×
false
38
68
false
4
8
false
false
三、解答题:(本题满分70分)
17.(本小题满分13分)
解:(Ⅰ)由false,得false.
所以false.
当false时,可求得false.
所以false,
false …………………………………………………7分
(Ⅱ)若选择条件①:
由false,得false.则false,解得false.
则false的取值范围false. …………………………………………………13分
若选择条件②:
因为false,false,
又false,所以false或false.
解得false或false.
则false的取值范围false或false. ……………………………………13分
18. (本小题满分13分)
解:(Ⅰ)false,falsefalse.
当false时,因为false,所以false恒成立,故false的单调递增区间为false;
当false时,令false,解得false,故当false时,false;
当false时,false,故false的单调递增区间为false
综合以上,当false时,false的单调递增区间为false;当false时,false的单调递增区间为false. …………………………………..7分
(Ⅱ) 设false,则false,false
由(Ⅰ)知,当false时,false在false上单调递增,即false当且仅当false 时等号成立.
故false 因false,故false,
所以false
所以false在区间false上单调递增,且false,所以当false时,false即
false. …………………………………..13分
19.(本小题满分14分)
解:
(Ⅰ) false
则估计观看电影《八佰》的观众年龄低于30岁的概率为0.57. …………………………..4分
(Ⅱ)设事件false为“第1次抽到男性观众”,事件false为“第2次抽到男性观众”.
已知第1次抽到男性观众,这时还剩下99人,其中女性观众39人,男性观众60人.因此,事件false发生的条件下,事件false发生的概率为
false. …………………………..8分(Ⅲ)零假设为
false:影片与观众性别独立,即男性和女性观众对这两部历史战争题材影片的选择没有差异.
影片
女性观众
男性观众
总计
《八佰》
47
53
100
《金刚川》
39
61
100
总计
86
114
200
根据false列联表中的数据可得
false false
根据小概率值false的独立性检验,没有充分证据推断false不成立,因此可以认为false成立,即认为男女观众对这两部历史战争题材影片的选择没有差异. ………………..14分
20.(本小题满分15分)
解:(Ⅰ)设false表示事件“第false次抽到的是优等产品”,因为是不放回抽样,所以:
false
所以falsefalse. ………………………..5分
(Ⅱ) false=0,1,2
false,false,false
false
0
1
2
false
false
false
false
false. ………………………..11分
(Ⅲ)设方案一产生的费用为false,
则false ,
false
0
1
2
false
0
280
480
false
false
false
false
false元.
设方案二产生的费用为false,
则false,false元.
由于false,故应该将不合格产品返厂再加工.
因此应选择方案一. ……………………..15分
21. (本小题满分15分)
解:(Ⅰ)因false,令false,解得false,
当false变化时,false的变化情况如下表:
false
false
1
false
false
false
0
false
false
单调递减
极小值false
单调递增
当false时,函数false取极小值false,无极大值. ……………………..5分
(Ⅱ)设false的较大零点为false,由(Ⅰ)知false在区间false上单调递增,且false,false,故false,则当false时,false,当false时,false.
当false时,false恒成立,即false恒成立.设false,则false,显然false与false同号,所以,false在false上单调递减,在false上单调递增,falsefalse,则false,又因false,所以false的最大值为3. ……………………..10分
(Ⅲ)因false,false
false,
当false时,false,false单调递增.
而false,false,
则方程false在false上有唯一实数根,即false
则false
要证:当false时,false,即证false.
设false,
则只需证明false在区间false上单调递增.
因false,
根据函数单调性容易判定false在false上单调递增,且false,故false,所以,false在false上单调递增,因false,则false.所以当false时,false. ……………………..15分
同课章节目录
