江苏省常州市教育学会2020-2021学年高二下学期期末考试数学试题 Word版含答案
文档属性
| 名称 | 江苏省常州市教育学会2020-2021学年高二下学期期末考试数学试题 Word版含答案 | 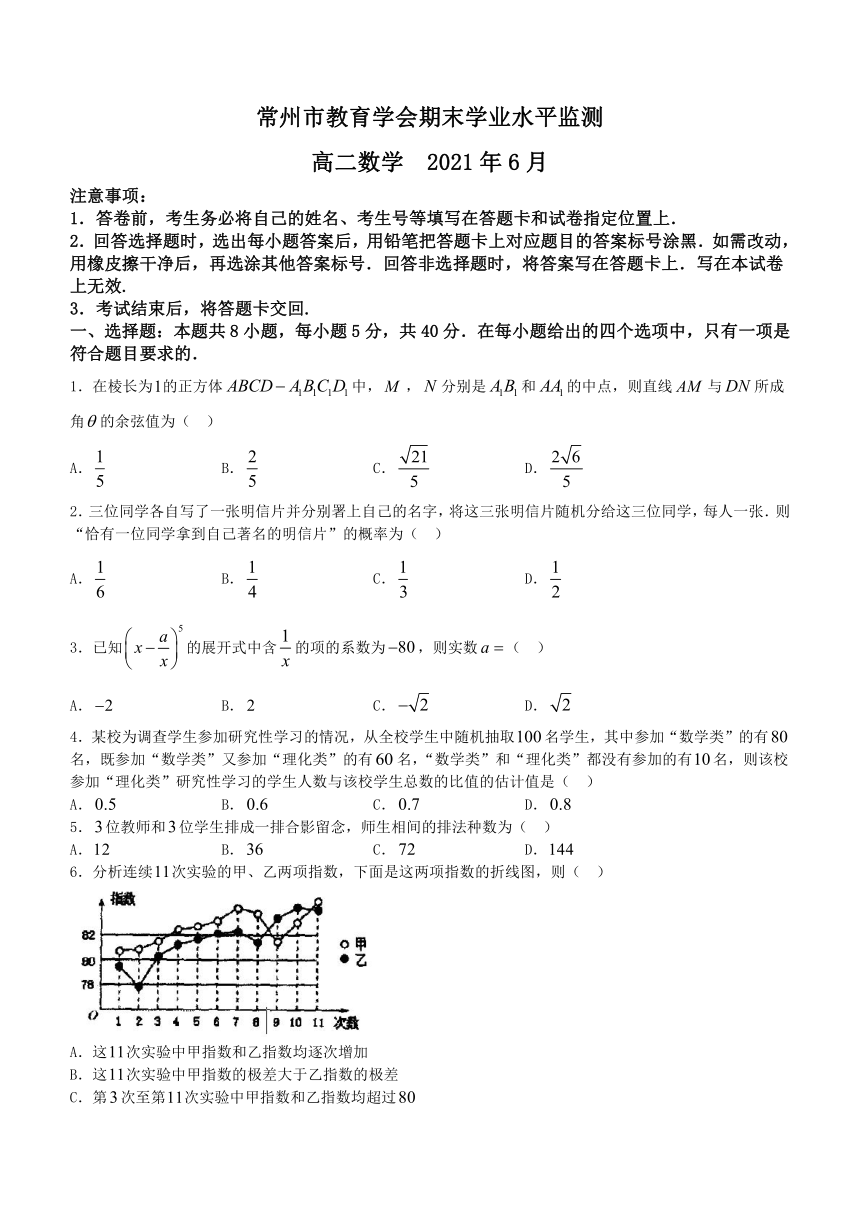 | |
| 格式 | docx | ||
| 文件大小 | 802.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-06 09:04:01 | ||
图片预览





文档简介
1031240011303000常州市教育学会期末学业水平监测
高二数学 2021年6月
注意事项:
1.答卷前,考生务必将自己的姓名、考生号等填写在答题卡和试卷指定位置上.
2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑.如需改动,用橡皮擦干净后,再选涂其他答案标号.回答非选择题时,将答案写在答题卡上.写在本试卷上无效.
3.考试结束后,将答题卡交回.
一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.在棱长为false的正方体false中,false,false分别是false和false的中点,则直线false与false所成角false的余弦值为( )
A.false B.false C.false D.false
2.三位同学各自写了一张明信片并分别署上自己的名字,将这三张明信片随机分给这三位同学,每人一张.则“恰有一位同学拿到自己著名的明信片”的概率为( )
A.false B.false C.false D.false
3.已知false的展开式中含false的项的系数为false,则实数false( )
A.false B.false C.false D.false
4.某校为调查学生参加研究性学习的情况,从全校学生中随机抽取false名学生,其中参加“数学类”的有false名,既参加“数学类”又参加“理化类”的有false名,“数学类”和“理化类”都没有参加的有false名,则该校参加“理化类”研究性学习的学生人数与该校学生总数的比值的估计值是( )
A.false B.false C.false D.false
5.false位教师和false位学生排成一排合影留念,师生相间的排法种数为( )
A.false B.false C.false D.false
6.分析连续false次实验的甲、乙两项指数,下面是这两项指数的折线图,则( )
A.这false次实验中甲指数和乙指数均逐次增加
B.这false次实验中甲指数的极差大于乙指数的极差
C.第false次至第false次实验中甲指数和乙指数均超过false
D.第false次至第false次实验中甲指数的增量小于乙指数的增量
7.false展开式中false项的系数为( )
A.false B.false C.false D.false
8.已知函数false的定义域为false,若false在false上为增函数,则称false为“false阶比增函数”.若函数false为“false阶比增函数",则实数false的取值范围是( )
A.false B.false C.false D.false
二、选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,有选错的得0分,部分选对的得2分.
9.小明用一枚质地均匀的硬币进行抛硬币实验,则下列说法正确的有( )
A.小明抛掷硬币false次,则该硬币正面向上的概率为false
B.小明连续抛掷硬币false次,则恰有false次正面向上的概率为false
C.小明连续抛掷硬币false次,则正面向上的次数恰好为false次
D.随着抛掷次数的增加,硬币正面向上的次数与抛掷次数的比值在false附近摆动,并趋于稳定
10.数据false的false组测量值为false,已知false,false,false,false.若false对false的线性回归方程记作false,则( )
附:线性回归方程false中,false,false,其中false为样本平均值.
A.false B.false
C.false与false正相关 D.false时,false的估计值为false
11.已知函数false(false为自然对数的底数),若false,则( )
A.false
B.false
C.当false时,false
D.当false时,false
12.在正三棱锥false中,设false,false,则( )
A.false的取值范围为(false)
B.当false时,正三棱锥false的高为false
C.false变大时,正三棱锥false的体积一定变大
D.false变大时,正三棱锥false的表面积一定变大
三、填空题:本题共4小题,每小题5分,共20分.
13.已知甲、乙两球落入盒子的概率分别为false和false.假定两球是否落入盒子互不影响,则甲、乙两球至少有一球落入盒子的概率为__________.
14.据《九章算术》中记载,“阳马”是以矩形为底面,一棱与底面垂直的四棱锥.现有一个“阳马”,false底面false,底面false是矩形,且false,false,false,则这个四棱锥外接球表面积为__________.
15.已知苏锡常镇四市联考中某校学生数学成绩false服从正态分布false,且false,则从该校学生中任选一名学生,该生的数学成绩超过false分的概率为__________.
16.已知函数false,若存在实数false,使得false成立,则实数false的所有可能取值构成的集合为__________.
四、解答题:本题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.
17.为鉴定某疫苗的效力,将false只实验鼠分为两组,其中一组接种疫苗,另一组不接种疫菌,然后对这false只实验鼠注射病原菌,其结果列于下表:
发病
没发病
合计
接种
false
false
没接种
false
false
合计
false
false
(false)求false,false的值,并判断是否有false的把握认为实验鼠是否发病与疫苗有关?
(false)若将(false)中的频率视为概率,从该批实验鼠中任取false只,设其中接种疫苗且发病的实验鼠的只数为随机变量false,求false的期望.
参考数据:独立性检验界值表:
falsefalse
false
false
false
false
false
false
false
false
false
false
false
其中,false,false(注:保留三位小数).
18.如图,在四棱锥false中,底面false为矩形,平面false平面false,false,false,false分别为false,false的中点.
(false)求证:false平面false;
(false)求证:平面false平面false.
19.某游客计划到常州的恐龙园、东方盐湖城、天目湖、春秋乐园这四个景点游览,若该游客游览恐龙园的概率为false,游览东方盐湖城、天目湖和春秋乐园的概率都是false,且该游客是否游览某个景点相互独立.记该游客游览的景点个数为随机变量false.
(false)求该游客至多游览一个景点的概率;
(false)求随机变量false的分布与期望.
20.已知函数false.
(1)当false时,求函数false的单调区间;
(2)若false对false恒成立,求实数false的取值范围.(false是自然对数的底数)
21.如图,在梯形false中,false,false在线段false上,且false.沿false将false折起,使点false到达点false的位置,满足false.
(1)证明:false平面false;
(2)若在梯形false中,false,折起后false在平面false上的射影false恰好是false与false的交点,求直线false与平面false所成角的正弦值.
22.已知函数false(false为自然对数的底数).
(1)求曲线false在点false处的切线方程:
(2)若方程false有两个不等的实数根false,false而,求证:false.
试卷答案
一、选择题:本题共8小题,每小题5分,共40分.
1.false 2.false 3.false 4.false 5.false 6.false 7.false 8.false
二、选择题:本题共4小题,每小题5分,共20分.
9.false 10.false 11.false 12.false
三、填空题:本题共4小题,每小题5分,共20分,
13.false 14.false 15.false 16.false
四、解答题:本题共6小题,共70分.
17.解:(false)false,false,false列联表如下:
发病
没发病
合计
接种
false
false
false
没接种
false
false
false
合计
false
false
false
false
所以,有false的把握认为实验鼠是否发病与疫苗有关.
(false)由(false)的列联表可知,接种疫苗且发病的实验鼠的只数占样本总数的频率为false,
从而在抽取的实验鼠中接种疫苗且发病的概率为false,
所以false,
所以随机变量false的期望为false.
18.解:(false)取false中点false,连结false,false,
false中,false,false为中点,
所以false,false,
false为矩形false的边false的中点,
所以false,false,
所以false,false,
所以四边形false是平行四边形,
所以false,
又因为false平面false,false平面false,
所以false平面false.
(false)因为平面false平面false,
平面false平面false,false,
false平面false,
所以false平面false,
又因为false平面false,
所以false,
又因为false,false,false,false平面false,
所以false平面false,
又因为false平面false,
所以平面false平面false.
19.解:(false)记“该游客游览恐龙园”为事件false,“该游客游览东方盐湖城”为事件false,“该游客游览天目湖”为事件false,“该游客游览春秋乐园”为事件false.
记“该游客至多游览一个景点”为事件false,
则false,false,
false,
其中false两两互斥,
false相互独立,
false
false
false
false,
答:该游客至多游览一个景点的概率为false.
(false)false的可能取值为false.
false,
false,
false
false,
false,,
随机变量false的分布列为
false
false
false
false
false
false
false
false
false
false
false
false
false.
20.解:(false)当false时,false,false,
令false,得false,
令false,
得false,
所以函数false的单调递增区间为false,单调递减区间为false.
(false)因为false对false恒成立,
由false,
得false,
所以false.
false等价于false.
令false,
则false,
令false,
得false.
false
false
false
false
false
false
false
false
false
单调递减
极小值false
单调递增
所以当false时,false.
令false,因为false,
所以false,
所以false;
故false.
综上false,
21.(false)因为false,false,
所以四边形false为菱形,
所以false,又false,false,false平面false,false平面false,
所以false平面false.
(false)因为false平面false,false平面false,false平面false,
所以false,false,
又false,
以false为原点,以false为正交基底,建立空间直角坐标系false.
在菱形false中,false,false.
所以false,false.
设false,
则false,false.
在菱形false中,false,
所以false,
在false中,由余弦定理得false,
所以false.
所以false,false,false,false,
false,false,false.
设平面false的法向量为false,
则false,false.
令false,则false,false.
所以false是平面false的一个法向量.
设直线false与平面false所成角为false,则
false.
所以直线false与平面false所成角的正弦值为false.
22.(false)false,false,false,
所以曲线false在false处的切线方程为false.
(false)令false,得false,列三行表如下
false
false
false
false
false
false
false
false
false
单调递减
false
单调递增
因为false有两个不等的实数根false,false,所以false,
不妨设false,
令false,false,
令false,false,
false
false
false
false
false
false
false
false
false
false
false
false
单调递减
极小值
单调递增
false
所以对任意false,false,
所以false,
即false,
所以false,
所以false,
所以false.
高二数学 2021年6月
注意事项:
1.答卷前,考生务必将自己的姓名、考生号等填写在答题卡和试卷指定位置上.
2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑.如需改动,用橡皮擦干净后,再选涂其他答案标号.回答非选择题时,将答案写在答题卡上.写在本试卷上无效.
3.考试结束后,将答题卡交回.
一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.在棱长为false的正方体false中,false,false分别是false和false的中点,则直线false与false所成角false的余弦值为( )
A.false B.false C.false D.false
2.三位同学各自写了一张明信片并分别署上自己的名字,将这三张明信片随机分给这三位同学,每人一张.则“恰有一位同学拿到自己著名的明信片”的概率为( )
A.false B.false C.false D.false
3.已知false的展开式中含false的项的系数为false,则实数false( )
A.false B.false C.false D.false
4.某校为调查学生参加研究性学习的情况,从全校学生中随机抽取false名学生,其中参加“数学类”的有false名,既参加“数学类”又参加“理化类”的有false名,“数学类”和“理化类”都没有参加的有false名,则该校参加“理化类”研究性学习的学生人数与该校学生总数的比值的估计值是( )
A.false B.false C.false D.false
5.false位教师和false位学生排成一排合影留念,师生相间的排法种数为( )
A.false B.false C.false D.false
6.分析连续false次实验的甲、乙两项指数,下面是这两项指数的折线图,则( )
A.这false次实验中甲指数和乙指数均逐次增加
B.这false次实验中甲指数的极差大于乙指数的极差
C.第false次至第false次实验中甲指数和乙指数均超过false
D.第false次至第false次实验中甲指数的增量小于乙指数的增量
7.false展开式中false项的系数为( )
A.false B.false C.false D.false
8.已知函数false的定义域为false,若false在false上为增函数,则称false为“false阶比增函数”.若函数false为“false阶比增函数",则实数false的取值范围是( )
A.false B.false C.false D.false
二、选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,有选错的得0分,部分选对的得2分.
9.小明用一枚质地均匀的硬币进行抛硬币实验,则下列说法正确的有( )
A.小明抛掷硬币false次,则该硬币正面向上的概率为false
B.小明连续抛掷硬币false次,则恰有false次正面向上的概率为false
C.小明连续抛掷硬币false次,则正面向上的次数恰好为false次
D.随着抛掷次数的增加,硬币正面向上的次数与抛掷次数的比值在false附近摆动,并趋于稳定
10.数据false的false组测量值为false,已知false,false,false,false.若false对false的线性回归方程记作false,则( )
附:线性回归方程false中,false,false,其中false为样本平均值.
A.false B.false
C.false与false正相关 D.false时,false的估计值为false
11.已知函数false(false为自然对数的底数),若false,则( )
A.false
B.false
C.当false时,false
D.当false时,false
12.在正三棱锥false中,设false,false,则( )
A.false的取值范围为(false)
B.当false时,正三棱锥false的高为false
C.false变大时,正三棱锥false的体积一定变大
D.false变大时,正三棱锥false的表面积一定变大
三、填空题:本题共4小题,每小题5分,共20分.
13.已知甲、乙两球落入盒子的概率分别为false和false.假定两球是否落入盒子互不影响,则甲、乙两球至少有一球落入盒子的概率为__________.
14.据《九章算术》中记载,“阳马”是以矩形为底面,一棱与底面垂直的四棱锥.现有一个“阳马”,false底面false,底面false是矩形,且false,false,false,则这个四棱锥外接球表面积为__________.
15.已知苏锡常镇四市联考中某校学生数学成绩false服从正态分布false,且false,则从该校学生中任选一名学生,该生的数学成绩超过false分的概率为__________.
16.已知函数false,若存在实数false,使得false成立,则实数false的所有可能取值构成的集合为__________.
四、解答题:本题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.
17.为鉴定某疫苗的效力,将false只实验鼠分为两组,其中一组接种疫苗,另一组不接种疫菌,然后对这false只实验鼠注射病原菌,其结果列于下表:
发病
没发病
合计
接种
false
false
没接种
false
false
合计
false
false
(false)求false,false的值,并判断是否有false的把握认为实验鼠是否发病与疫苗有关?
(false)若将(false)中的频率视为概率,从该批实验鼠中任取false只,设其中接种疫苗且发病的实验鼠的只数为随机变量false,求false的期望.
参考数据:独立性检验界值表:
falsefalse
false
false
false
false
false
false
false
false
false
false
false
其中,false,false(注:保留三位小数).
18.如图,在四棱锥false中,底面false为矩形,平面false平面false,false,false,false分别为false,false的中点.
(false)求证:false平面false;
(false)求证:平面false平面false.
19.某游客计划到常州的恐龙园、东方盐湖城、天目湖、春秋乐园这四个景点游览,若该游客游览恐龙园的概率为false,游览东方盐湖城、天目湖和春秋乐园的概率都是false,且该游客是否游览某个景点相互独立.记该游客游览的景点个数为随机变量false.
(false)求该游客至多游览一个景点的概率;
(false)求随机变量false的分布与期望.
20.已知函数false.
(1)当false时,求函数false的单调区间;
(2)若false对false恒成立,求实数false的取值范围.(false是自然对数的底数)
21.如图,在梯形false中,false,false在线段false上,且false.沿false将false折起,使点false到达点false的位置,满足false.
(1)证明:false平面false;
(2)若在梯形false中,false,折起后false在平面false上的射影false恰好是false与false的交点,求直线false与平面false所成角的正弦值.
22.已知函数false(false为自然对数的底数).
(1)求曲线false在点false处的切线方程:
(2)若方程false有两个不等的实数根false,false而,求证:false.
试卷答案
一、选择题:本题共8小题,每小题5分,共40分.
1.false 2.false 3.false 4.false 5.false 6.false 7.false 8.false
二、选择题:本题共4小题,每小题5分,共20分.
9.false 10.false 11.false 12.false
三、填空题:本题共4小题,每小题5分,共20分,
13.false 14.false 15.false 16.false
四、解答题:本题共6小题,共70分.
17.解:(false)false,false,false列联表如下:
发病
没发病
合计
接种
false
false
false
没接种
false
false
false
合计
false
false
false
false
所以,有false的把握认为实验鼠是否发病与疫苗有关.
(false)由(false)的列联表可知,接种疫苗且发病的实验鼠的只数占样本总数的频率为false,
从而在抽取的实验鼠中接种疫苗且发病的概率为false,
所以false,
所以随机变量false的期望为false.
18.解:(false)取false中点false,连结false,false,
false中,false,false为中点,
所以false,false,
false为矩形false的边false的中点,
所以false,false,
所以false,false,
所以四边形false是平行四边形,
所以false,
又因为false平面false,false平面false,
所以false平面false.
(false)因为平面false平面false,
平面false平面false,false,
false平面false,
所以false平面false,
又因为false平面false,
所以false,
又因为false,false,false,false平面false,
所以false平面false,
又因为false平面false,
所以平面false平面false.
19.解:(false)记“该游客游览恐龙园”为事件false,“该游客游览东方盐湖城”为事件false,“该游客游览天目湖”为事件false,“该游客游览春秋乐园”为事件false.
记“该游客至多游览一个景点”为事件false,
则false,false,
false,
其中false两两互斥,
false相互独立,
false
false
false
false,
答:该游客至多游览一个景点的概率为false.
(false)false的可能取值为false.
false,
false,
false
false,
false,,
随机变量false的分布列为
false
false
false
false
false
false
false
false
false
false
false
false
false.
20.解:(false)当false时,false,false,
令false,得false,
令false,
得false,
所以函数false的单调递增区间为false,单调递减区间为false.
(false)因为false对false恒成立,
由false,
得false,
所以false.
false等价于false.
令false,
则false,
令false,
得false.
false
false
false
false
false
false
false
false
false
单调递减
极小值false
单调递增
所以当false时,false.
令false,因为false,
所以false,
所以false;
故false.
综上false,
21.(false)因为false,false,
所以四边形false为菱形,
所以false,又false,false,false平面false,false平面false,
所以false平面false.
(false)因为false平面false,false平面false,false平面false,
所以false,false,
又false,
以false为原点,以false为正交基底,建立空间直角坐标系false.
在菱形false中,false,false.
所以false,false.
设false,
则false,false.
在菱形false中,false,
所以false,
在false中,由余弦定理得false,
所以false.
所以false,false,false,false,
false,false,false.
设平面false的法向量为false,
则false,false.
令false,则false,false.
所以false是平面false的一个法向量.
设直线false与平面false所成角为false,则
false.
所以直线false与平面false所成角的正弦值为false.
22.(false)false,false,false,
所以曲线false在false处的切线方程为false.
(false)令false,得false,列三行表如下
false
false
false
false
false
false
false
false
false
单调递减
false
单调递增
因为false有两个不等的实数根false,false,所以false,
不妨设false,
令false,false,
令false,false,
false
false
false
false
false
false
false
false
false
false
false
false
单调递减
极小值
单调递增
false
所以对任意false,false,
所以false,
即false,
所以false,
所以false,
所以false.
同课章节目录
