2021年暑假自主学习北师大版九年级数学上册1.3正方形的性质与判定优生提升训练(Word版,附答案解析)
文档属性
| 名称 | 2021年暑假自主学习北师大版九年级数学上册1.3正方形的性质与判定优生提升训练(Word版,附答案解析) |  | |
| 格式 | doc | ||
| 文件大小 | 300.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-06 15:18:20 | ||
图片预览

文档简介
2021年北师大版九年级数学上册《1.3正方形的性质与判定》暑假自主学习
优生提升训练(附答案)
1.下列说法正确的是( )
A.一组对边平行,另一组对边相等的四边形是平行四边形
B.三个角都是直角的四边形是矩形
C.对角线相等的平行四边形是菱形
D.一组邻边相等的平行四边形是正方形
2.下列性质中,正方形具有而矩形不一定具有的性质是( )
A.对角线互相垂直 B.对角线互相平分
C.对角线相等 D.四个角都是直角
3.如图,在△ABC中,点E、D、F分别在边AB、BC、CA上,且DE∥CA,DF∥BA,下列四个判断中,不正确的是( )
A.四边形AEDF是平行四边形
B.如果AD=EF,那么四边形AEDF是矩形
C.如果AD平分∠EAF,那么四边形AEDF是菱形
D.如果AD⊥BC且AB=AC,那么四边形AEDF是正方形
4.下列说法正确的有几个( )
①对角线互相平分的四边形是平行四边形; ②对角线互相垂直的四边形是菱形;
③对角线互相垂直且相等的平行四边形是正方形;④对角线相等的平行四边形是矩形.
A.1个 B.2个 C.3个 D.4个
5.如图,将n个边长都为2的正方形按如图所示摆放,点A1,A2,…An分别是正方形的中心,则这n个正方形重叠部分的面积之和是( )
A.n B.n﹣1 C.4(n﹣1) D.4n
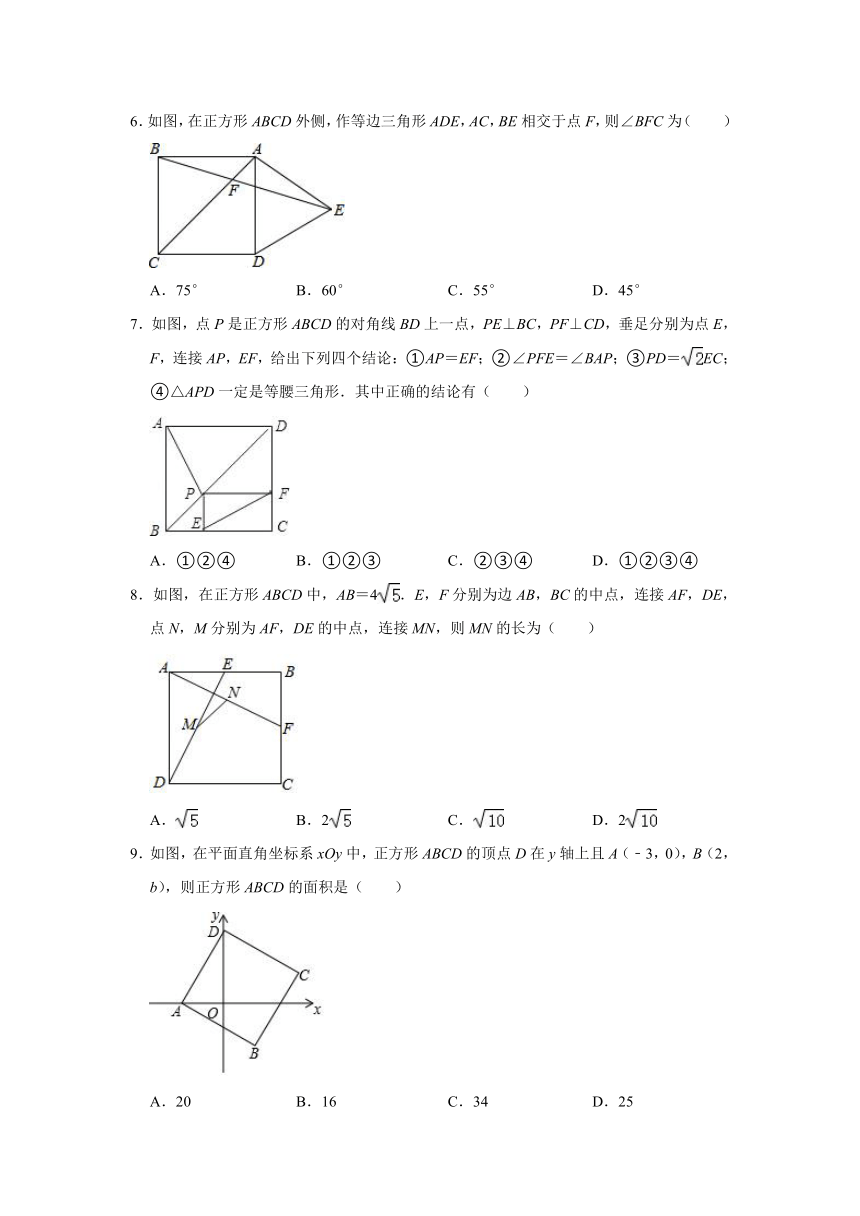
6.如图,在正方形ABCD外侧,作等边三角形ADE,AC,BE相交于点F,则∠BFC为( )
A.75° B.60° C.55° D.45°
7.如图,点P是正方形ABCD的对角线BD上一点,PE⊥BC,PF⊥CD,垂足分别为点E,F,连接AP,EF,给出下列四个结论:①AP=EF;②∠PFE=∠BAP;③PD=EC;④△APD一定是等腰三角形.其中正确的结论有( )
A.①②④ B.①②③ C.②③④ D.①②③④
8.如图,在正方形ABCD中,AB=4.E,F分别为边AB,BC的中点,连接AF,DE,点N,M分别为AF,DE的中点,连接MN,则MN的长为( )
A. B.2 C. D.2
9.如图,在平面直角坐标系xOy中,正方形ABCD的顶点D在y轴上且A(﹣3,0),B(2,b),则正方形ABCD的面积是( )
A.20 B.16 C.34 D.25
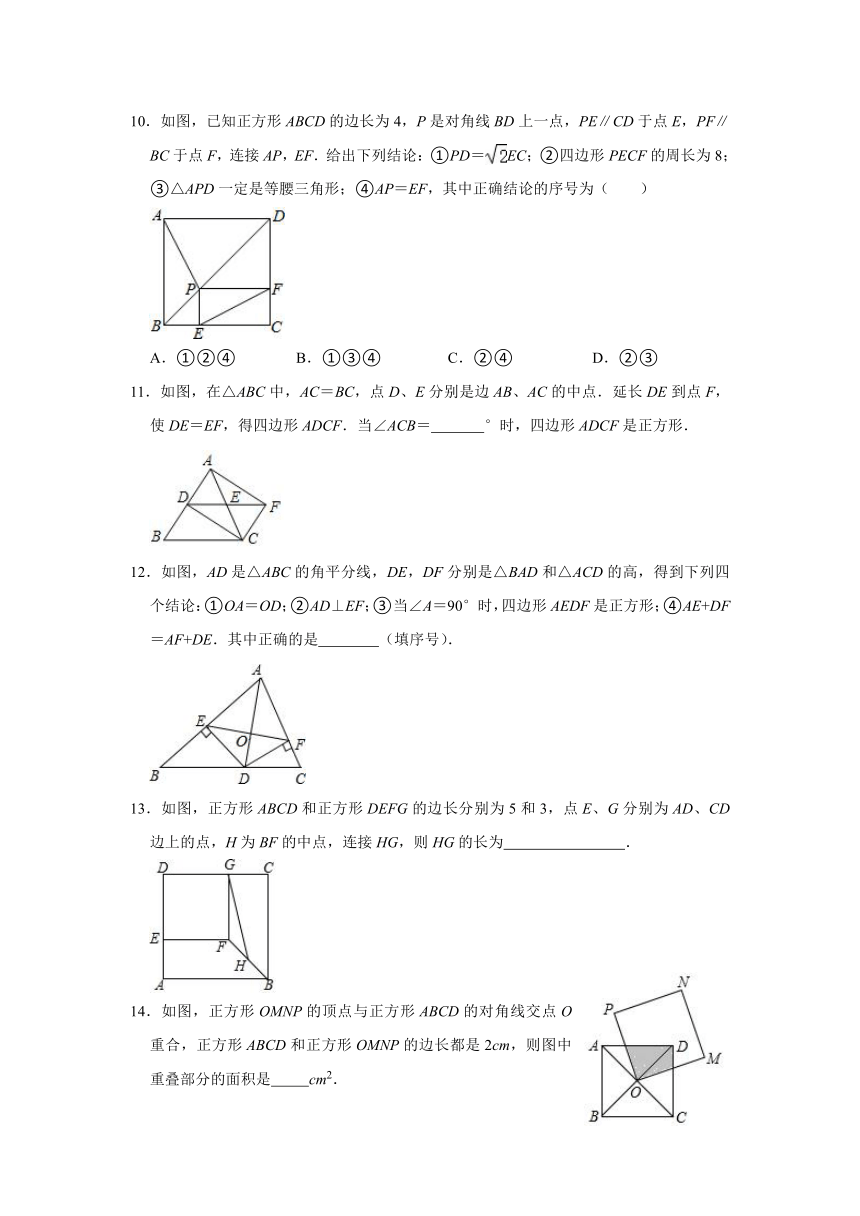
10.如图,已知正方形ABCD的边长为4,P是对角线BD上一点,PE∥CD于点E,PF∥BC于点F,连接AP,EF.给出下列结论:①PD=EC;②四边形PECF的周长为8;③△APD一定是等腰三角形;④AP=EF,其中正确结论的序号为( )
A.①②④ B.①③④ C.②④ D.②③
11.如图,在△ABC中,AC=BC,点D、E分别是边AB、AC的中点.延长DE到点F,使DE=EF,得四边形ADCF.当∠ACB= °时,四边形ADCF是正方形.
12.如图,AD是△ABC的角平分线,DE,DF分别是△BAD和△ACD的高,得到下列四个结论:①OA=OD;②AD⊥EF;③当∠A=90°时,四边形AEDF是正方形;④AE+DF=AF+DE.其中正确的是 (填序号).
13.如图,正方形ABCD和正方形DEFG的边长分别为5和3,点E、G分别为AD、CD边上的点,H为BF的中点,连接HG,则HG的长为 .
14.如图,正方形OMNP的顶点与正方形ABCD的对角线交点O重合,正方形ABCD和正方形OMNP的边长都是2cm,则图中重叠部分的面积是 cm2.
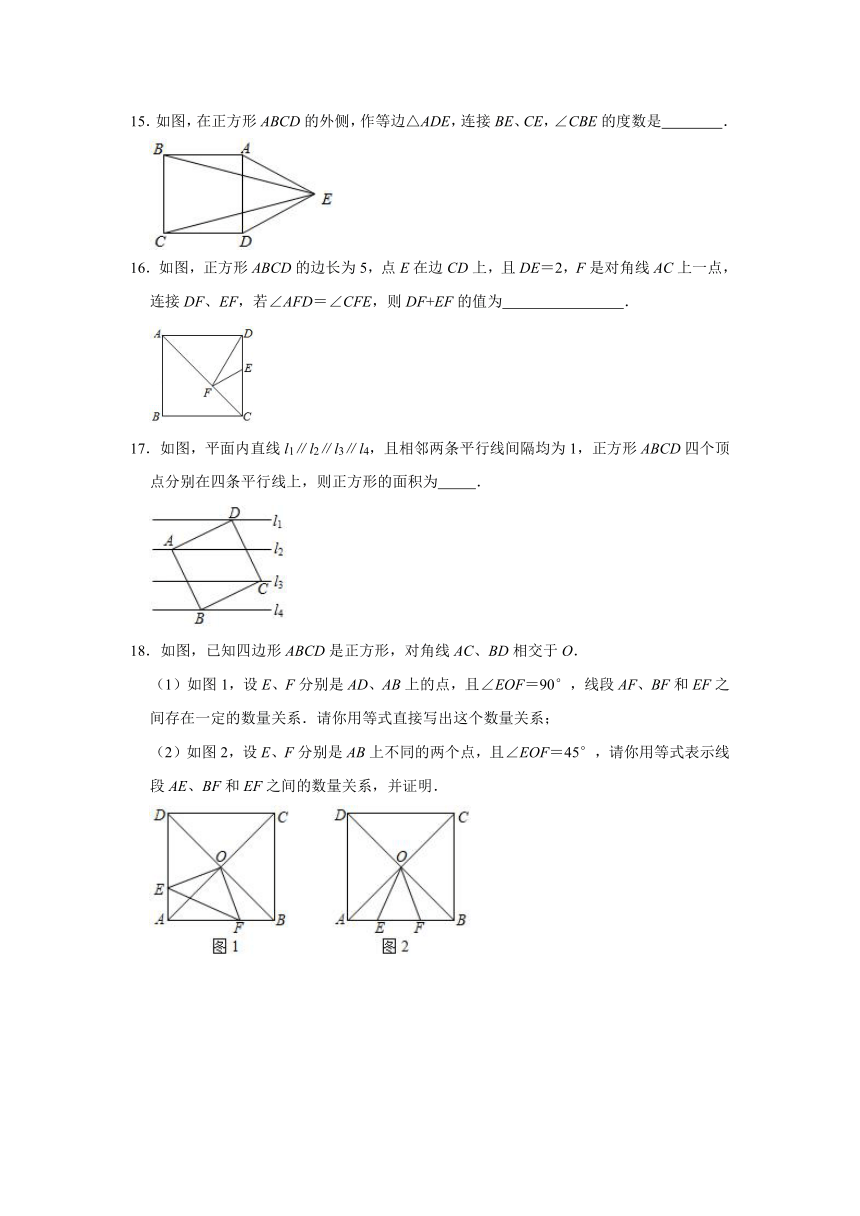
15.如图,在正方形ABCD的外侧,作等边△ADE,连接BE、CE,∠CBE的度数是 .
16.如图,正方形ABCD的边长为5,点E在边CD上,且DE=2,F是对角线AC上一点,连接DF、EF,若∠AFD=∠CFE,则DF+EF的值为 .
17.如图,平面内直线l1∥l2∥l3∥l4,且相邻两条平行线间隔均为1,正方形ABCD四个顶点分别在四条平行线上,则正方形的面积为 .
18.如图,已知四边形ABCD是正方形,对角线AC、BD相交于O.
(1)如图1,设E、F分别是AD、AB上的点,且∠EOF=90°,线段AF、BF和EF之间存在一定的数量关系.请你用等式直接写出这个数量关系;
(2)如图2,设E、F分别是AB上不同的两个点,且∠EOF=45°,请你用等式表示线段AE、BF和EF之间的数量关系,并证明.
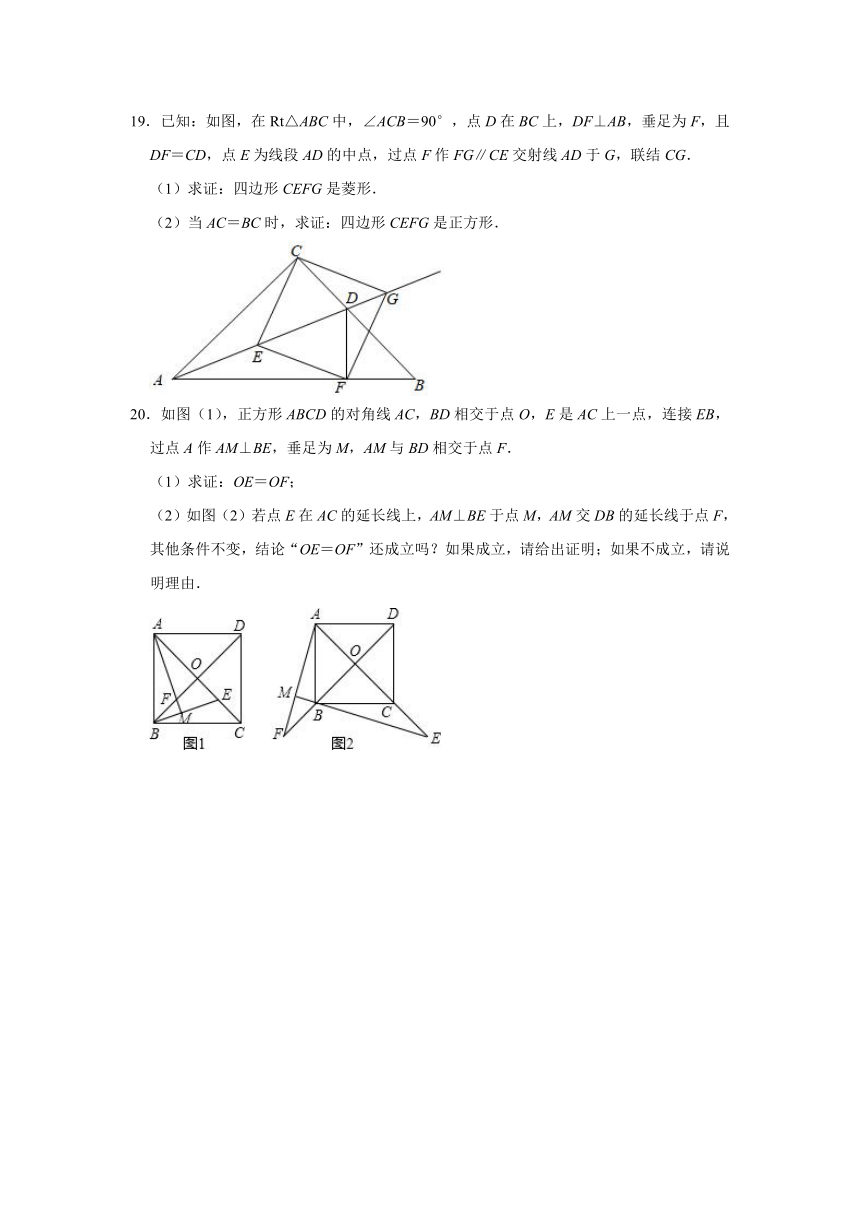
19.已知:如图,在Rt△ABC中,∠ACB=90°,点D在BC上,DF⊥AB,垂足为F,且DF=CD,点E为线段AD的中点,过点F作FG∥CE交射线AD于G,联结CG.
(1)求证:四边形CEFG是菱形.
(2)当AC=BC时,求证:四边形CEFG是正方形.
20.如图(1),正方形ABCD的对角线AC,BD相交于点O,E是AC上一点,连接EB,过点A作AM⊥BE,垂足为M,AM与BD相交于点F.
(1)求证:OE=OF;
(2)如图(2)若点E在AC的延长线上,AM⊥BE于点M,AM交DB的延长线于点F,其他条件不变,结论“OE=OF”还成立吗?如果成立,请给出证明;如果不成立,请说明理由.
参考答案
1.解:A.一组对边平行,另一组对边相等的四边形也可能是等腰梯形,所以A选项错误,故不符合题意;
B.三个角都是直角的四边形是矩形,所以B选正确,故符合题意;
C.对角线相等的平行四边形是矩形,所以C选项错误,不符合题意;
D.一组邻边相等的平行四边形是菱形,所以D选项错误,不符合题意;
故选:B.
2.解:A、正方形的对角线互相垂直平分,矩形的对角线互相平分但不一定垂直,故本选项正确.
B、正方形和矩形的对角线都互相平分,故本选项错误;
C、正方形和矩形的对角线都相等,故本选项错误;
D、正方形和矩形的四个角都是直角,故本选项错误;
故选:A.
3.解:A、因为DE∥CA,DF∥BA,所以四边形AEDF是平行四边形.故A选项正确.
B、如果AD=EF,四边形AEDF是平行四边形,所以四边形AEDF是矩形.故B选项正确.
C、因为AD平分∠EAF,所以∠EAD=∠FAD,∵∠FAD=∠EDA,∠EAD=∠FDA,∴EAD=∠EDA,∴AE=DE,又因为四边形AEDF是平行四边形,所以是菱形.故C选项正确.
D、如果AD⊥BC且AB=AC,所以四边形AEDF是菱形,故D选项错误.
故选:D.
4.解:①对角线互相平分的四边形是平行四边形,故正确;
②对角线互相垂直平分的四边形是菱形,故错误;
③对角线互相垂直且相等的平行四边形是正方形,故正确;
④对角线相等的平行四边形是矩形,故正确;
故选:C.
5.解:由题意可得一个阴影部分面积等于正方形面积的,即是×4=1,
n个这样的正方形重叠部分(阴影部分)的面积和为:1×(n﹣1)=n﹣1.
故选:B.
6.解:∵四边形ABCD是正方形,
∴∠BAD=90°,AB=AD,∠BAF=45°,
∵△ADE是等边三角形,
∴∠DAE=60°,AD=AE,
∴∠BAE=90°+60°=150°,AB=AE,
∴∠ABE=∠AEB=(180°﹣150°)=15°,
∴∠BFC=∠BAF+∠ABE=45°+15°=60°;
故选:B.
7.解:延长PF交AB于点G,
∵PF⊥CD,AB∥CD,
∴PG⊥AB,即∠PGB=90°.
∵PE⊥BC,PF⊥CD,
∴四边形GBEP为矩形,
又∵∠PBE=∠BPE=45°,
∴BE=PE,
∴四边形GBEP为正方形,四边形PFCE为矩形.
∴GB=BE=EP=GP,
∴GP=PE,AG=CE=PF,
又∠AGP=∠C=90°,
∴△AGP≌△FPE(SAS).
∴AP=EF,∠PFE=∠BAP,
故①、②正确;
在Rt△PDF中,由勾股定理得PD=,
故③正确;
∵P在BD上,
∴当AP=DP、AP=AD、PD=DA时,△APD才是等腰三角形,
∴△APD是等腰三角形共有3种情况,故④错误.
∴正确答案有①②③,
故选:B.
8.解:连接AM,延长AM交CD于G,连接FG,
∵四边形ABCD是正方形,
∴AB=CD=BC=4,AB∥CD,∠C=90°,
∴∠AEM=∠GDM,∠EAM=∠DGM,
∵M为DE的中点,
∴ME=MD,
在△AEM和GDM中,
,
∴△AEM≌△GDM(AAS),
∴AM=MG,AE=DG=AB=CD,
∴CG=CD=2,
∵点N为AF的中点,
∴MN=FG,
∵F为BC的中点,
∴CF=BC=2,
∴FG==2,
∴MN=,
故选:C.
9.解:作BM⊥x轴于M.
∵四边形ABCD是正方形,
∴AD=AB,∠DAB=90°,
∴∠DAO+∠BAM=90°,∠BAM+∠ABM=90°,
∴∠DAO=∠ABM,
∵∠AOD=∠AMB=90°,
∴在△DAO和△ABM中,
∴△DAO≌△ABM(AAS),
∴OA=BM,AM=OD,
∵A(﹣3,0),B(2,b),
∴OA=3,OM=2,
∴OD=AM=5,
∴AD==,
∴正方形ABCD的面积=34,
故选:C.
10.解:①∵PE⊥BC,PF⊥CD,
∴∠PEF=∠PFC=90°,
又∠C=90°,
∴四边形PECF是矩形,
∴EC=PF.
∵四边形ABCD是正方形,
∴∠PDF=45°,
∴△PDF是等腰直角三角形,
∴PD=PF=EC,
故①正确;
②∵PE⊥BC,PF⊥CD,∠BCD=90°,
∴四边形PECF为矩形,
∴四边形PECF的周长=2CE+2PE=2CE+2BE=2BC=8,
故②正确;
③∵点P是正方形ABCD的对角线BD上任意一点,∠ADP=45°,
∴当∠PAD=45°或67.5°或90°时,△APD是等腰三角形,
除此之外,△APD不是等腰三角形,
故③错误.
④∵四边形PECF为矩形,
∴PC=EF,∠PFE=∠ECP,
∵正方形为轴对称图形,
∴AP=PC,
∴AP=EF,
故④正确;
故选:A.
11.解:当∠ACB=90°时,四边形ADCF是正方形,
理由是:∵AC=BC,∠ACB=90°,
∴∠CAB=∠CBA=45°,
∵AC=BC,D为AB的中点,
∴CD⊥AB,CD平分∠ACB,
∴∠ADC=90°,∠ACD=ACB==45°=∠CAB,
∴AD=CD,
∵E为AC的中点,
∴AE=CE,
∵DE=EF,
∴四边形ADCF是平行四边形,
∵∠CDA=90°,AD=CD,
∴四边形ADCF是正方形,
即当∠ACB=90°时,四边形ADCF是正方形,
故答案为:90.
12.解:如果OA=OD,则四边形AEDF是矩形,没有说∠A=90°,不符合题意,故①错误;
∵AD是△ABC的角平分线,
∴∠EAD=∠FAD,
在△AED和△AFD中,
∴△AED≌△AFD(AAS),
∴AE=AF,DE=DF,
∴AE+DF=AF+DE,故④正确;
∵在△AEO和△AFO中,
,
∴△AEO≌△AFO(SAS),
∴EO=FO,
又∵AE=AF,
∴AO是EF的中垂线,
∴AD⊥EF,故②正确;
∵当∠A=90°时,四边形AEDF的四个角都是直角,
∴四边形AEDF是矩形,
又∵DE=DF,
∴四边形AEDF是正方形,故③正确.
综上可得:正确的是:②③④,
故答案为:②③④.
13.解:延长GF交AB于P,过H作MN⊥CD于M,交AB于N,
∵四边形ABCD是正方形,
∴AB∥CD,BC⊥CD,
∴MN⊥AB,
∵四边形DEFG是正方形,
∴FG⊥CD,
∴FG∥HM∥BC,
∵H是BF的中点,
∴PN=BN=CM=GM=CG==1,
∴HN是△BFP的中位线,
∴HN=FP=1,
∴MH=5﹣1=4,
Rt△GHM中,由勾股定理得:GH==.
故答案为:.
14.解:如图,∵正方形ABCD和正方形OMNP的边长都是2cm,
∴OA=OD,∠AOD=∠POM=90°,∠OAG=∠DOF=45°,
在△AOG和△DOF中,
∵,
∴△AOG≌△DOF(ASA),
∴S四边形OFDG=S△AOD===1;
则图中重叠部分的面积是1cm2,
故答案为:1.
15.解:∵正方形ABCD,
∴∠ABC=∠BAD=90°,AB=AD,
∵等边△ADE,
∴AD=AE,∠DAE=60°,
∴∠BAE=∠BAD+∠DAE=150°,AB=AE,
∴∠ABE=15°,
∴∠CBE=∠ABC﹣∠ABE=75°,
故答案为:75°.
16.解:过D作DH⊥AC于H,如图:
∵正方形ABCD的边长为5,DE=2,
∴∠DAC=∠DCA=45°,AC=5,CE=3,
∵∠AFD=∠CFE,
而AF+CF=5,
∴AF=,
∵AD=5,DH⊥AC,∠DAC=45°,
∴AH==DH,
∴HF=AF﹣AH=,
Rt△DHF中,DF==,
∵,
∴EF=,
∴DF+EF=.
故答案为:.
方法2:连接BF,如图:
由正方形ABCD对称性可得:DF=BF,∠AFD=∠AFB,
∵∠AFD=∠CFE,
∴∠AFB=∠CFE,
∴∠AFB+∠BFC=∠CFE+∠BFC=180°,
∴B、F、E共线,
∵正方形ABCD的边长为5,DE=2,
∴BE==,
∴DF+EF=BF+EF=BE=,
故答案为:.
17.解:过C点作EF⊥l2,交l1于E点,交l4于F点.
∵l1∥l2∥l3∥l4,EF⊥l2,
∴EF⊥l1,EF⊥l4,
即∠CED=∠BFC=90°.
∵ABCD为正方形,
∴∠BCD=90°.
∴∠DCE+∠BCF=90°.
又∵∠DCE+∠CDE=90°,
∴∠CDE=∠BCF.
在△CDE和△BCF中,
∴△CDE≌△BCF(AAS),
∴BF=CE=2.
∵CF=1,
∴BC2=12+22=5,
即正方形ABCD的面积为5.
故答案为:5.
18.解:(1)EF2=AF2+BF2.
理由:如图1,∵四边形ABCD是正方形,
∴OA=OB,∠OAE=∠OBF=45°,AC⊥BD,
∴∠EOF=∠AOB=90°,
∴∠EOA=∠FOB,
在△EOA和△FOB中,
,
∴△EOA≌△FOB(ASA),
∴AE=BF,
在Rt△EAF中,EF2=AE2+AF2=AF2+BF2;
(2)在BC上取一点H,使得BH=AE.
∵四边形ABCD是正方形,
∴OA=OB,∠OAE=∠OBH,∠AOB=90°,
在△OAE和△OBH中,
∴△OAE≌△OBH(SAS),
∴AE=BH,∠AOE=∠BOH,OE=OH,
∵∠EOF=45°,
∴∠AOE+∠BOF=45°,
∴∠BOF+∠BOH=45°,
∴∠FOE=∠FOH=45°,
在△FOE和△FOH中?,
,
∴△FOE≌△FOH(SAS),
∴EF=FH,
∵∠FBH=90°,
∴FH2=BF2+BH2,
∴EF2=BF2+AE2,
19.证明:(1)∵∠ACB=90°,DF⊥AB,
∴∠DFA=90°,
在Rt△ACD与Rt△AFD中,
,
∴Rt△ACD≌Rt△AFD(HL),
∴∠CAD=∠FAD,AC=AF,
在△ACG与△AFG中,
,
∴△ACG≌△AFG(SAS),
∴CG=FG,∠CGA=∠FGA,
∵FG∥CE,
∴∠FGA=∠CEG,
∴∠CGE=∠CEG,
∴CE=CG,
∵点E为线段AD的中点,∠ACB=90°,∠DFA=90°,
∴CE=AD,EF=AD,AE=AD,
∴CE=EF=AE,
∴CE=CG=GF=EF,
∴四边形CEFG是菱形;
(2)∵AC=BC,∠ACB=90°,
∴∠CAB=∠B,
∵∠CAB+∠B+∠ACB=180°,
∴∠CAB==45°,
由(1)知,∠CAD=∠FAD,
∴∠CAD=∠FAD=22.5°,
∵CE=EF=AE,
∴∠CAE=∠ECA=22.5°,∠FAE=∠EFA=22.5°,
∴∠CEG=∠CAE+∠ECA=45°,∠FEG=∠FAE+∠EFA=45°,
∴∠CEF=∠CEG+∠GEF=90°,
∵四边形CEFG是菱形,
∴四边形CEFG是正方形.
20.解:(1)∵四边形ABCD是正方形.
∴∠BOE=∠AOF=90°,OB=OA.
又∵AM⊥BE,
∴∠MEA+∠MAE=90°=∠AFO+∠MAE,
∴∠MEA=∠AFO.
在△BOE和△AOF中,
∵,
∴△BOE≌△AOF.
∴OE=OF.
(2)OE=OF成立.
∵四边形ABCD是正方形,
∴∠BOE=∠AOF=90°,OB=OA.
又∵AM⊥BE,
∴∠F+∠MBF=90°,
∠E+∠OBE=90°,
又∵∠MBF=∠OBE,
∴∠F=∠E.
在△BOE和△AOF中,
∵,
∴△BOE≌△AOF.
∴OE=OF.
优生提升训练(附答案)
1.下列说法正确的是( )
A.一组对边平行,另一组对边相等的四边形是平行四边形
B.三个角都是直角的四边形是矩形
C.对角线相等的平行四边形是菱形
D.一组邻边相等的平行四边形是正方形
2.下列性质中,正方形具有而矩形不一定具有的性质是( )
A.对角线互相垂直 B.对角线互相平分
C.对角线相等 D.四个角都是直角
3.如图,在△ABC中,点E、D、F分别在边AB、BC、CA上,且DE∥CA,DF∥BA,下列四个判断中,不正确的是( )
A.四边形AEDF是平行四边形
B.如果AD=EF,那么四边形AEDF是矩形
C.如果AD平分∠EAF,那么四边形AEDF是菱形
D.如果AD⊥BC且AB=AC,那么四边形AEDF是正方形
4.下列说法正确的有几个( )
①对角线互相平分的四边形是平行四边形; ②对角线互相垂直的四边形是菱形;
③对角线互相垂直且相等的平行四边形是正方形;④对角线相等的平行四边形是矩形.
A.1个 B.2个 C.3个 D.4个
5.如图,将n个边长都为2的正方形按如图所示摆放,点A1,A2,…An分别是正方形的中心,则这n个正方形重叠部分的面积之和是( )
A.n B.n﹣1 C.4(n﹣1) D.4n
6.如图,在正方形ABCD外侧,作等边三角形ADE,AC,BE相交于点F,则∠BFC为( )
A.75° B.60° C.55° D.45°
7.如图,点P是正方形ABCD的对角线BD上一点,PE⊥BC,PF⊥CD,垂足分别为点E,F,连接AP,EF,给出下列四个结论:①AP=EF;②∠PFE=∠BAP;③PD=EC;④△APD一定是等腰三角形.其中正确的结论有( )
A.①②④ B.①②③ C.②③④ D.①②③④
8.如图,在正方形ABCD中,AB=4.E,F分别为边AB,BC的中点,连接AF,DE,点N,M分别为AF,DE的中点,连接MN,则MN的长为( )
A. B.2 C. D.2
9.如图,在平面直角坐标系xOy中,正方形ABCD的顶点D在y轴上且A(﹣3,0),B(2,b),则正方形ABCD的面积是( )
A.20 B.16 C.34 D.25
10.如图,已知正方形ABCD的边长为4,P是对角线BD上一点,PE∥CD于点E,PF∥BC于点F,连接AP,EF.给出下列结论:①PD=EC;②四边形PECF的周长为8;③△APD一定是等腰三角形;④AP=EF,其中正确结论的序号为( )
A.①②④ B.①③④ C.②④ D.②③
11.如图,在△ABC中,AC=BC,点D、E分别是边AB、AC的中点.延长DE到点F,使DE=EF,得四边形ADCF.当∠ACB= °时,四边形ADCF是正方形.
12.如图,AD是△ABC的角平分线,DE,DF分别是△BAD和△ACD的高,得到下列四个结论:①OA=OD;②AD⊥EF;③当∠A=90°时,四边形AEDF是正方形;④AE+DF=AF+DE.其中正确的是 (填序号).
13.如图,正方形ABCD和正方形DEFG的边长分别为5和3,点E、G分别为AD、CD边上的点,H为BF的中点,连接HG,则HG的长为 .
14.如图,正方形OMNP的顶点与正方形ABCD的对角线交点O重合,正方形ABCD和正方形OMNP的边长都是2cm,则图中重叠部分的面积是 cm2.
15.如图,在正方形ABCD的外侧,作等边△ADE,连接BE、CE,∠CBE的度数是 .
16.如图,正方形ABCD的边长为5,点E在边CD上,且DE=2,F是对角线AC上一点,连接DF、EF,若∠AFD=∠CFE,则DF+EF的值为 .
17.如图,平面内直线l1∥l2∥l3∥l4,且相邻两条平行线间隔均为1,正方形ABCD四个顶点分别在四条平行线上,则正方形的面积为 .
18.如图,已知四边形ABCD是正方形,对角线AC、BD相交于O.
(1)如图1,设E、F分别是AD、AB上的点,且∠EOF=90°,线段AF、BF和EF之间存在一定的数量关系.请你用等式直接写出这个数量关系;
(2)如图2,设E、F分别是AB上不同的两个点,且∠EOF=45°,请你用等式表示线段AE、BF和EF之间的数量关系,并证明.
19.已知:如图,在Rt△ABC中,∠ACB=90°,点D在BC上,DF⊥AB,垂足为F,且DF=CD,点E为线段AD的中点,过点F作FG∥CE交射线AD于G,联结CG.
(1)求证:四边形CEFG是菱形.
(2)当AC=BC时,求证:四边形CEFG是正方形.
20.如图(1),正方形ABCD的对角线AC,BD相交于点O,E是AC上一点,连接EB,过点A作AM⊥BE,垂足为M,AM与BD相交于点F.
(1)求证:OE=OF;
(2)如图(2)若点E在AC的延长线上,AM⊥BE于点M,AM交DB的延长线于点F,其他条件不变,结论“OE=OF”还成立吗?如果成立,请给出证明;如果不成立,请说明理由.
参考答案
1.解:A.一组对边平行,另一组对边相等的四边形也可能是等腰梯形,所以A选项错误,故不符合题意;
B.三个角都是直角的四边形是矩形,所以B选正确,故符合题意;
C.对角线相等的平行四边形是矩形,所以C选项错误,不符合题意;
D.一组邻边相等的平行四边形是菱形,所以D选项错误,不符合题意;
故选:B.
2.解:A、正方形的对角线互相垂直平分,矩形的对角线互相平分但不一定垂直,故本选项正确.
B、正方形和矩形的对角线都互相平分,故本选项错误;
C、正方形和矩形的对角线都相等,故本选项错误;
D、正方形和矩形的四个角都是直角,故本选项错误;
故选:A.
3.解:A、因为DE∥CA,DF∥BA,所以四边形AEDF是平行四边形.故A选项正确.
B、如果AD=EF,四边形AEDF是平行四边形,所以四边形AEDF是矩形.故B选项正确.
C、因为AD平分∠EAF,所以∠EAD=∠FAD,∵∠FAD=∠EDA,∠EAD=∠FDA,∴EAD=∠EDA,∴AE=DE,又因为四边形AEDF是平行四边形,所以是菱形.故C选项正确.
D、如果AD⊥BC且AB=AC,所以四边形AEDF是菱形,故D选项错误.
故选:D.
4.解:①对角线互相平分的四边形是平行四边形,故正确;
②对角线互相垂直平分的四边形是菱形,故错误;
③对角线互相垂直且相等的平行四边形是正方形,故正确;
④对角线相等的平行四边形是矩形,故正确;
故选:C.
5.解:由题意可得一个阴影部分面积等于正方形面积的,即是×4=1,
n个这样的正方形重叠部分(阴影部分)的面积和为:1×(n﹣1)=n﹣1.
故选:B.
6.解:∵四边形ABCD是正方形,
∴∠BAD=90°,AB=AD,∠BAF=45°,
∵△ADE是等边三角形,
∴∠DAE=60°,AD=AE,
∴∠BAE=90°+60°=150°,AB=AE,
∴∠ABE=∠AEB=(180°﹣150°)=15°,
∴∠BFC=∠BAF+∠ABE=45°+15°=60°;
故选:B.
7.解:延长PF交AB于点G,
∵PF⊥CD,AB∥CD,
∴PG⊥AB,即∠PGB=90°.
∵PE⊥BC,PF⊥CD,
∴四边形GBEP为矩形,
又∵∠PBE=∠BPE=45°,
∴BE=PE,
∴四边形GBEP为正方形,四边形PFCE为矩形.
∴GB=BE=EP=GP,
∴GP=PE,AG=CE=PF,
又∠AGP=∠C=90°,
∴△AGP≌△FPE(SAS).
∴AP=EF,∠PFE=∠BAP,
故①、②正确;
在Rt△PDF中,由勾股定理得PD=,
故③正确;
∵P在BD上,
∴当AP=DP、AP=AD、PD=DA时,△APD才是等腰三角形,
∴△APD是等腰三角形共有3种情况,故④错误.
∴正确答案有①②③,
故选:B.
8.解:连接AM,延长AM交CD于G,连接FG,
∵四边形ABCD是正方形,
∴AB=CD=BC=4,AB∥CD,∠C=90°,
∴∠AEM=∠GDM,∠EAM=∠DGM,
∵M为DE的中点,
∴ME=MD,
在△AEM和GDM中,
,
∴△AEM≌△GDM(AAS),
∴AM=MG,AE=DG=AB=CD,
∴CG=CD=2,
∵点N为AF的中点,
∴MN=FG,
∵F为BC的中点,
∴CF=BC=2,
∴FG==2,
∴MN=,
故选:C.
9.解:作BM⊥x轴于M.
∵四边形ABCD是正方形,
∴AD=AB,∠DAB=90°,
∴∠DAO+∠BAM=90°,∠BAM+∠ABM=90°,
∴∠DAO=∠ABM,
∵∠AOD=∠AMB=90°,
∴在△DAO和△ABM中,
∴△DAO≌△ABM(AAS),
∴OA=BM,AM=OD,
∵A(﹣3,0),B(2,b),
∴OA=3,OM=2,
∴OD=AM=5,
∴AD==,
∴正方形ABCD的面积=34,
故选:C.
10.解:①∵PE⊥BC,PF⊥CD,
∴∠PEF=∠PFC=90°,
又∠C=90°,
∴四边形PECF是矩形,
∴EC=PF.
∵四边形ABCD是正方形,
∴∠PDF=45°,
∴△PDF是等腰直角三角形,
∴PD=PF=EC,
故①正确;
②∵PE⊥BC,PF⊥CD,∠BCD=90°,
∴四边形PECF为矩形,
∴四边形PECF的周长=2CE+2PE=2CE+2BE=2BC=8,
故②正确;
③∵点P是正方形ABCD的对角线BD上任意一点,∠ADP=45°,
∴当∠PAD=45°或67.5°或90°时,△APD是等腰三角形,
除此之外,△APD不是等腰三角形,
故③错误.
④∵四边形PECF为矩形,
∴PC=EF,∠PFE=∠ECP,
∵正方形为轴对称图形,
∴AP=PC,
∴AP=EF,
故④正确;
故选:A.
11.解:当∠ACB=90°时,四边形ADCF是正方形,
理由是:∵AC=BC,∠ACB=90°,
∴∠CAB=∠CBA=45°,
∵AC=BC,D为AB的中点,
∴CD⊥AB,CD平分∠ACB,
∴∠ADC=90°,∠ACD=ACB==45°=∠CAB,
∴AD=CD,
∵E为AC的中点,
∴AE=CE,
∵DE=EF,
∴四边形ADCF是平行四边形,
∵∠CDA=90°,AD=CD,
∴四边形ADCF是正方形,
即当∠ACB=90°时,四边形ADCF是正方形,
故答案为:90.
12.解:如果OA=OD,则四边形AEDF是矩形,没有说∠A=90°,不符合题意,故①错误;
∵AD是△ABC的角平分线,
∴∠EAD=∠FAD,
在△AED和△AFD中,
∴△AED≌△AFD(AAS),
∴AE=AF,DE=DF,
∴AE+DF=AF+DE,故④正确;
∵在△AEO和△AFO中,
,
∴△AEO≌△AFO(SAS),
∴EO=FO,
又∵AE=AF,
∴AO是EF的中垂线,
∴AD⊥EF,故②正确;
∵当∠A=90°时,四边形AEDF的四个角都是直角,
∴四边形AEDF是矩形,
又∵DE=DF,
∴四边形AEDF是正方形,故③正确.
综上可得:正确的是:②③④,
故答案为:②③④.
13.解:延长GF交AB于P,过H作MN⊥CD于M,交AB于N,
∵四边形ABCD是正方形,
∴AB∥CD,BC⊥CD,
∴MN⊥AB,
∵四边形DEFG是正方形,
∴FG⊥CD,
∴FG∥HM∥BC,
∵H是BF的中点,
∴PN=BN=CM=GM=CG==1,
∴HN是△BFP的中位线,
∴HN=FP=1,
∴MH=5﹣1=4,
Rt△GHM中,由勾股定理得:GH==.
故答案为:.
14.解:如图,∵正方形ABCD和正方形OMNP的边长都是2cm,
∴OA=OD,∠AOD=∠POM=90°,∠OAG=∠DOF=45°,
在△AOG和△DOF中,
∵,
∴△AOG≌△DOF(ASA),
∴S四边形OFDG=S△AOD===1;
则图中重叠部分的面积是1cm2,
故答案为:1.
15.解:∵正方形ABCD,
∴∠ABC=∠BAD=90°,AB=AD,
∵等边△ADE,
∴AD=AE,∠DAE=60°,
∴∠BAE=∠BAD+∠DAE=150°,AB=AE,
∴∠ABE=15°,
∴∠CBE=∠ABC﹣∠ABE=75°,
故答案为:75°.
16.解:过D作DH⊥AC于H,如图:
∵正方形ABCD的边长为5,DE=2,
∴∠DAC=∠DCA=45°,AC=5,CE=3,
∵∠AFD=∠CFE,
而AF+CF=5,
∴AF=,
∵AD=5,DH⊥AC,∠DAC=45°,
∴AH==DH,
∴HF=AF﹣AH=,
Rt△DHF中,DF==,
∵,
∴EF=,
∴DF+EF=.
故答案为:.
方法2:连接BF,如图:
由正方形ABCD对称性可得:DF=BF,∠AFD=∠AFB,
∵∠AFD=∠CFE,
∴∠AFB=∠CFE,
∴∠AFB+∠BFC=∠CFE+∠BFC=180°,
∴B、F、E共线,
∵正方形ABCD的边长为5,DE=2,
∴BE==,
∴DF+EF=BF+EF=BE=,
故答案为:.
17.解:过C点作EF⊥l2,交l1于E点,交l4于F点.
∵l1∥l2∥l3∥l4,EF⊥l2,
∴EF⊥l1,EF⊥l4,
即∠CED=∠BFC=90°.
∵ABCD为正方形,
∴∠BCD=90°.
∴∠DCE+∠BCF=90°.
又∵∠DCE+∠CDE=90°,
∴∠CDE=∠BCF.
在△CDE和△BCF中,
∴△CDE≌△BCF(AAS),
∴BF=CE=2.
∵CF=1,
∴BC2=12+22=5,
即正方形ABCD的面积为5.
故答案为:5.
18.解:(1)EF2=AF2+BF2.
理由:如图1,∵四边形ABCD是正方形,
∴OA=OB,∠OAE=∠OBF=45°,AC⊥BD,
∴∠EOF=∠AOB=90°,
∴∠EOA=∠FOB,
在△EOA和△FOB中,
,
∴△EOA≌△FOB(ASA),
∴AE=BF,
在Rt△EAF中,EF2=AE2+AF2=AF2+BF2;
(2)在BC上取一点H,使得BH=AE.
∵四边形ABCD是正方形,
∴OA=OB,∠OAE=∠OBH,∠AOB=90°,
在△OAE和△OBH中,
∴△OAE≌△OBH(SAS),
∴AE=BH,∠AOE=∠BOH,OE=OH,
∵∠EOF=45°,
∴∠AOE+∠BOF=45°,
∴∠BOF+∠BOH=45°,
∴∠FOE=∠FOH=45°,
在△FOE和△FOH中?,
,
∴△FOE≌△FOH(SAS),
∴EF=FH,
∵∠FBH=90°,
∴FH2=BF2+BH2,
∴EF2=BF2+AE2,
19.证明:(1)∵∠ACB=90°,DF⊥AB,
∴∠DFA=90°,
在Rt△ACD与Rt△AFD中,
,
∴Rt△ACD≌Rt△AFD(HL),
∴∠CAD=∠FAD,AC=AF,
在△ACG与△AFG中,
,
∴△ACG≌△AFG(SAS),
∴CG=FG,∠CGA=∠FGA,
∵FG∥CE,
∴∠FGA=∠CEG,
∴∠CGE=∠CEG,
∴CE=CG,
∵点E为线段AD的中点,∠ACB=90°,∠DFA=90°,
∴CE=AD,EF=AD,AE=AD,
∴CE=EF=AE,
∴CE=CG=GF=EF,
∴四边形CEFG是菱形;
(2)∵AC=BC,∠ACB=90°,
∴∠CAB=∠B,
∵∠CAB+∠B+∠ACB=180°,
∴∠CAB==45°,
由(1)知,∠CAD=∠FAD,
∴∠CAD=∠FAD=22.5°,
∵CE=EF=AE,
∴∠CAE=∠ECA=22.5°,∠FAE=∠EFA=22.5°,
∴∠CEG=∠CAE+∠ECA=45°,∠FEG=∠FAE+∠EFA=45°,
∴∠CEF=∠CEG+∠GEF=90°,
∵四边形CEFG是菱形,
∴四边形CEFG是正方形.
20.解:(1)∵四边形ABCD是正方形.
∴∠BOE=∠AOF=90°,OB=OA.
又∵AM⊥BE,
∴∠MEA+∠MAE=90°=∠AFO+∠MAE,
∴∠MEA=∠AFO.
在△BOE和△AOF中,
∵,
∴△BOE≌△AOF.
∴OE=OF.
(2)OE=OF成立.
∵四边形ABCD是正方形,
∴∠BOE=∠AOF=90°,OB=OA.
又∵AM⊥BE,
∴∠F+∠MBF=90°,
∠E+∠OBE=90°,
又∵∠MBF=∠OBE,
∴∠F=∠E.
在△BOE和△AOF中,
∵,
∴△BOE≌△AOF.
∴OE=OF.
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
