山东省潍坊市青州市2019-2020学年下学期八年级期末考试数学试卷(word版含答案)
文档属性
| 名称 | 山东省潍坊市青州市2019-2020学年下学期八年级期末考试数学试卷(word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 214.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-06 16:55:50 | ||
图片预览


文档简介
2019-2020学年山东省潍坊市青州市八年级(下)期末数学试卷
一、选择题(本题共12小题,在每小题给出的四个选项中,只有一个是正确的,请把正确的选项选出来,每小题选对得3分,满分36分.多选、不选、错选均记零分.)
1.下列图形中,既是中心对称图形又是轴对称图形的是( )
A. B.
C. D.
2.下列计算正确的是( )
A. B. C. D.
3.若x>y,且(a﹣3)x<(a﹣3)y,则a的值可能是( )
A.5 B.4 C.3 D.0
4.若最简二次根式是同类二次根式,则x的值为( )
A. B. C.x=1 D.x=﹣1
5.如图,小方格都是边长为1的正方形,则△ABC中BC边上的高等于( )
A.2 B. C.2 D.
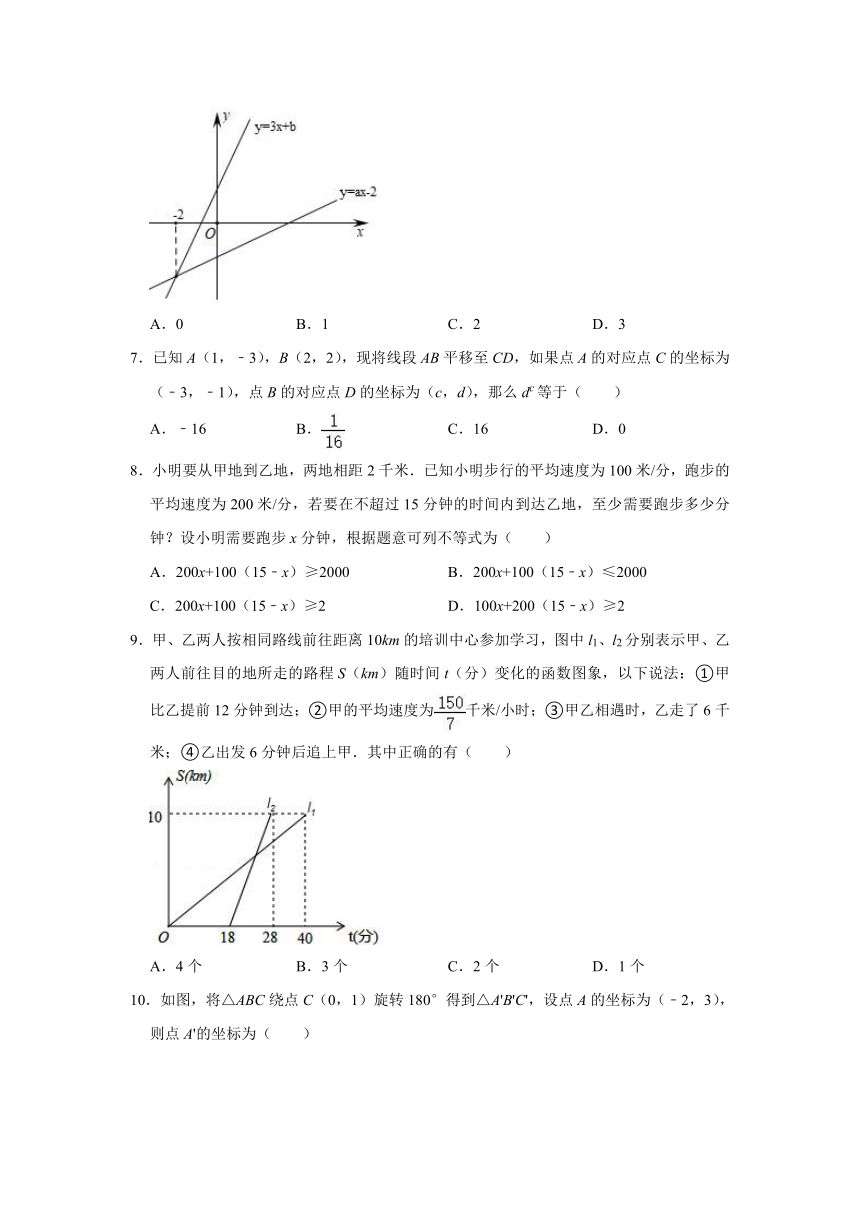
6.如图,已知直线y=3x+b与y=ax﹣2的交点的横坐标为﹣2,根据图象有下列3个结论:①a>0;②b<0;③x>﹣2是不等式3x+b>ax﹣2的解集.其中正确的个数是( )
A.0 B.1 C.2 D.3
7.已知A(1,﹣3),B(2,2),现将线段AB平移至CD,如果点A的对应点C的坐标为(﹣3,﹣1),点B的对应点D的坐标为(c,d),那么dc等于( )
A.﹣16 B. C.16 D.0
8.小明要从甲地到乙地,两地相距2千米.已知小明步行的平均速度为100米/分,跑步的平均速度为200米/分,若要在不超过15分钟的时间内到达乙地,至少需要跑步多少分钟?设小明需要跑步x分钟,根据题意可列不等式为( )
A.200x+100(15﹣x)≥2000 B.200x+100(15﹣x)≤2000
C.200x+100(15﹣x)≥2 D.100x+200(15﹣x)≥2
9.甲、乙两人按相同路线前往距离10km的培训中心参加学习,图中l1、l2分别表示甲、乙两人前往目的地所走的路程S(km)随时间t(分)变化的函数图象,以下说法:①甲比乙提前12分钟到达;②甲的平均速度为千米/小时;③甲乙相遇时,乙走了6千米;④乙出发6分钟后追上甲.其中正确的有( )
A.4个 B.3个 C.2个 D.1个
10.如图,将△ABC绕点C(0,1)旋转180°得到△A'B'C',设点A的坐标为(﹣2,3),则点A'的坐标为( )
A.(2,﹣3) B.(﹣1,2) C.(2,﹣2) D.(2,﹣1)
11.设直线y=kx+6与y=(k+1)x+6(k是正整数)及x轴围成的三角形面积为Sk(k=1,2,3,…),则S5的值等于( )
A. B. C.1 D.3
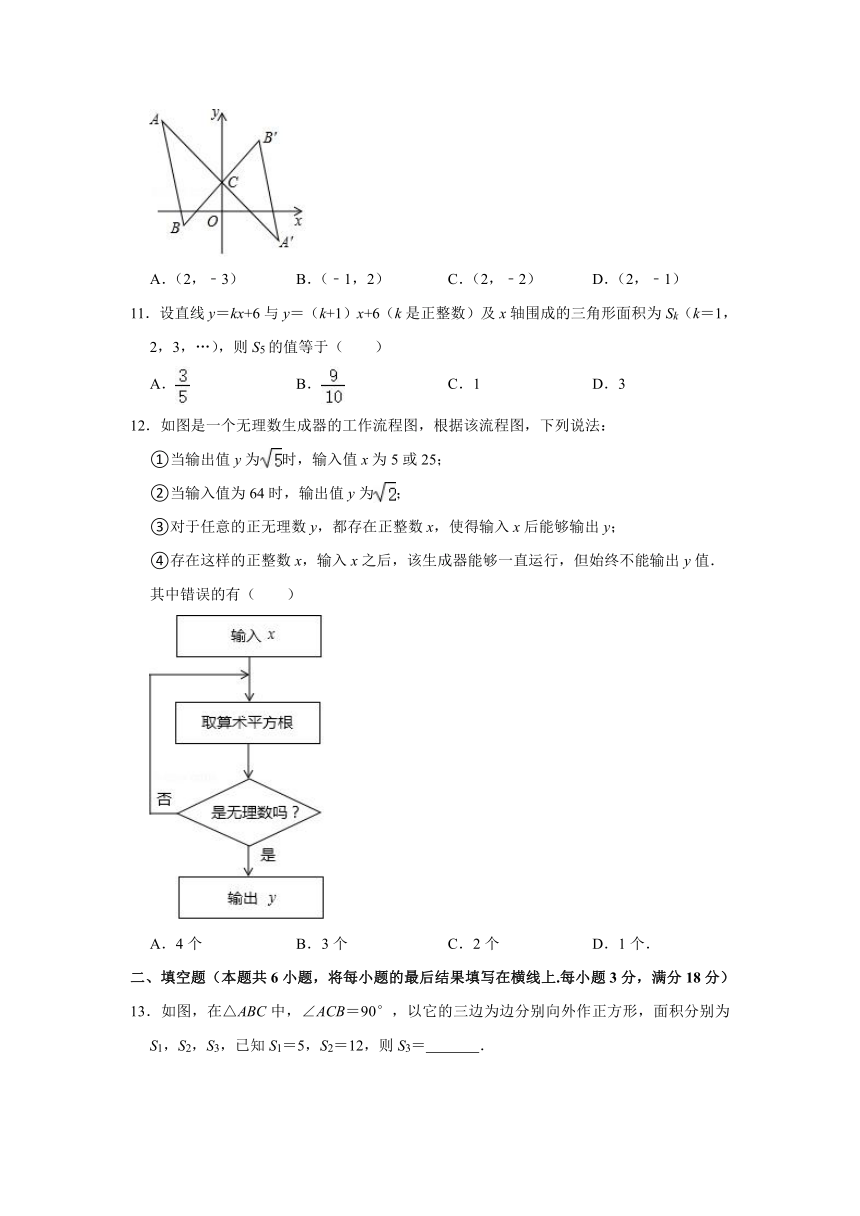
12.如图是一个无理数生成器的工作流程图,根据该流程图,下列说法:
①当输出值y为时,输入值x为5或25;
②当输入值为64时,输出值y为;
③对于任意的正无理数y,都存在正整数x,使得输入x后能够输出y;
④存在这样的正整数x,输入x之后,该生成器能够一直运行,但始终不能输出y值.
其中错误的有( )
A.4个 B.3个 C.2个 D.1个.
二、填空题(本题共6小题,将每小题的最后结果填写在横线上.每小题3分,满分18分)
13.如图,在△ABC中,∠ACB=90°,以它的三边为边分别向外作正方形,面积分别为S1,S2,S3,已知S1=5,S2=12,则S3= .
14.一次函数y=(m+1)x+2m﹣1的图象不经过第二象限,则m的取值范围是 .
15.如图,△OAB绕点O顺时针旋转42°得到△ODC,点D恰好落在AB上,且∠AOC=108°,则∠B度数是 .
16.已知,则代数式的值等于 .
17.已知关于x的不等式组的整数解共有5个,则a的取值范围是 .
18.已知线段EF两个端点的坐标为E(x1,y1),F(x2,y2),若点M(x0,y0)是线段EF的中点,则有x0=.在平面直角坐标系中有三个点A(1,﹣1)、B(﹣1,﹣1)、C(0,1),点P(0,2)关于点A的对称点记为P1,P1关于点B的对称点记为P2,P2关于点C的对称点记为P3,…,按此规律继续以A、B、C三点为对称中心,重复前面的操作,依次得到点P4,P5,P6,…,则点P2020的坐标是 .
三、解答题(本题共7小题,共66分.解答应写出文字说明、证明过程或推演步骤.)
19.(10分)(1)解不等式2(x+8)>3(x﹣2)+1,并把它的解集在数轴上表示出来;
(2)解不等式组:.
20.(8分)计算
(1);
(2).
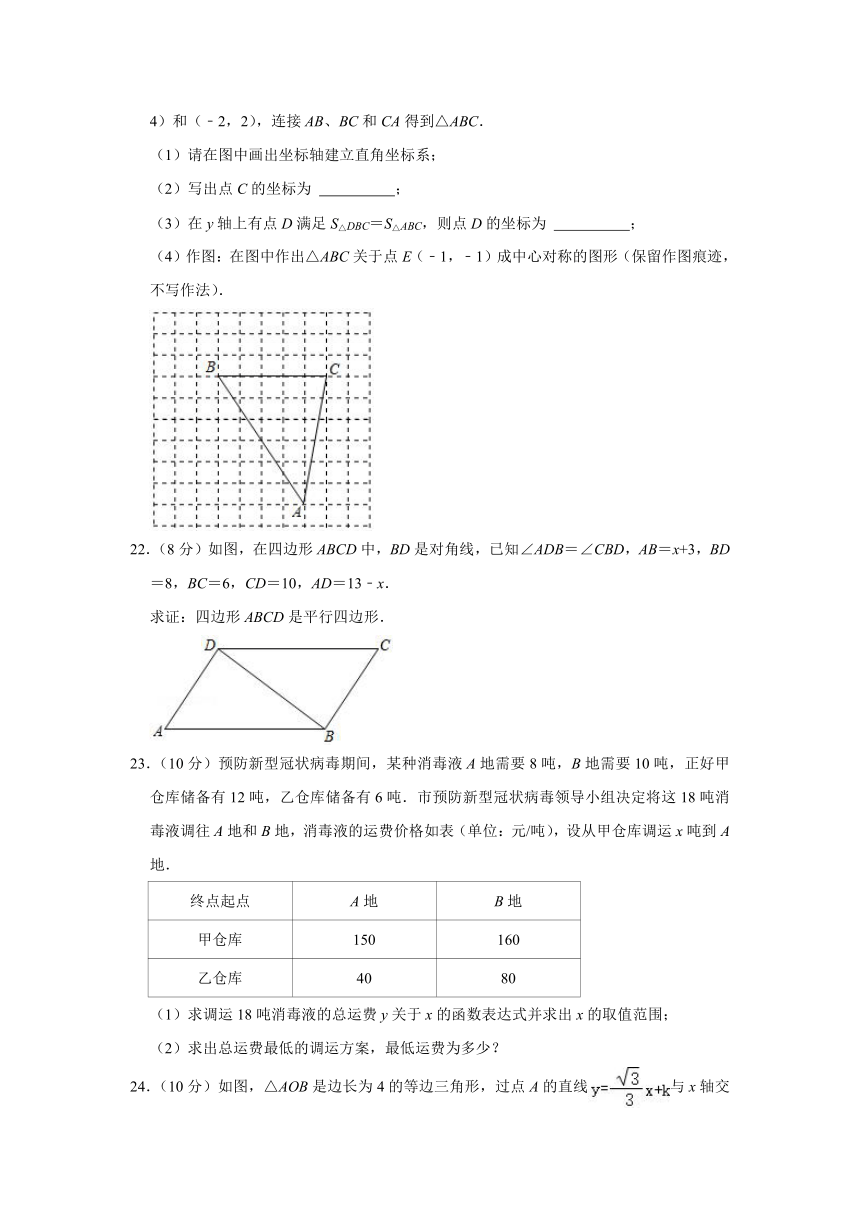
21.(8分)如图,在每个小正方形边长为1的方格纸中,A点和B点的坐标分别为(2,﹣4)和(﹣2,2),连接AB、BC和CA得到△ABC.
(1)请在图中画出坐标轴建立直角坐标系;
(2)写出点C的坐标为 ;
(3)在y轴上有点D满足S△DBC=S△ABC,则点D的坐标为 ;
(4)作图:在图中作出△ABC关于点E(﹣1,﹣1)成中心对称的图形(保留作图痕迹,不写作法).
22.(8分)如图,在四边形ABCD中,BD是对角线,已知∠ADB=∠CBD,AB=x+3,BD=8,BC=6,CD=10,AD=13﹣x.
求证:四边形ABCD是平行四边形.
23.(10分)预防新型冠状病毒期间,某种消毒液A地需要8吨,B地需要10吨,正好甲仓库储备有12吨,乙仓库储备有6吨.市预防新型冠状病毒领导小组决定将这18吨消毒液调往A地和B地,消毒液的运费价格如表(单位:元/吨),设从甲仓库调运x吨到A地.
终点起点 A地 B地
甲仓库 150 160
乙仓库 40 80
(1)求调运18吨消毒液的总运费y关于x的函数表达式并求出x的取值范围;
(2)求出总运费最低的调运方案,最低运费为多少?
24.(10分)如图,△AOB是边长为4的等边三角形,过点A的直线与x轴交于点C.
(1)求点A的坐标;
(2)求直线AC的函数表达式;
(3)若点P(m,n)是线段AC上的动点(不与A、C重合),设△ABP的面积为S,求S关于m的函数表达式及m的取值范围.
25.(12分)如图①,四边形ABCD是边长为4的正方形,M是正方形对角线BD(不含B、D两个端点)上任意一点,将△BAM绕点B逆时针旋转60°得到△BEN,连接EA、MN;P是AD的中点,连接PM.
(1)AM+PM的最小值等于 ;
(2)求证:△BNM是等边三角形;
(3)如图②,以B为坐标原点建立平面直角坐标系,若点M使得AM+BM+CM的值最小,求M点的坐标.
参考答案
一、选择题(本题共12小题,在每小题给出的四个选项中,只有一个是正确的,请把正确的选项选出来,每小题选对得3分,满分36分.多选、不选、错选均记零分.)
1. A.
2. D.
3. D.
4. C.
5. B.
6. C.
7. B.
8. A.
9. C.
10. D.
11. A.
12. B.
二、填空题(本题共6小题,将每小题的最后结果填写在横线上.每小题3分,满分18分)
13. 17.
14.﹣1<m≤.
15. 45°.
16. 5.
17.﹣3<a≤﹣2.
18.(﹣2,﹣2).
三、解答题(本题共7小题,共66分.解答应写出文字说明、证明过程或推演步骤.)
19.
解:(1)去括号,得:2x+16>3x﹣6+1,
移项,得:2x﹣3x>﹣6+1﹣16,
合并同类项,得:﹣x>﹣21,
系数化为1,得:x<21,
表示在数轴上如下:
(2)解不等式①得:x≤2,
解不等式②得:x>﹣1,
则不等式组的解集为﹣1<x≤2.
20.
解:(1)原式=﹣4+15﹣3﹣4+2
=6;
(2)原式=×2+×5﹣5×2﹣5×5
=6+10﹣10﹣25
=﹣19.
21.
解:(1)平面直角坐标系如图所示.
(2)C(3,2),
故答案为:(3,2).
(3)设D(0,m),则有×5×|2﹣m|×5=×5×6,
解得m=﹣4或8,
∴满足条件的点D的坐标为(0,﹣4)或(0,8),
故答案为:(0,﹣4)或(0,8).
(4)如图,△A′B′C′即为所求.
22.
证明:∵BD=8,BC=6,CD=10,
∴BD2+BC2=CD2,
∴△BCD是直角三角形,∠CBD=90°,
∵∠ADB=∠CBD,
∴AD∥BC,∠ADB=90°,
∴AD2+BD2=AB2,
即(13﹣x)2+82=(x+3)2,
解得:x=7,
∴AD=6,
∴AD=BC,
又∵AD∥BC,
∴四边形ABCD是平行四边形.
23.
解:(1)设从甲仓库调运x吨到A地,则从甲仓库调运(12﹣x)吨到B地,从乙仓库调运(8﹣x)吨到A地,从乙仓库调运10﹣(12﹣x)=(x﹣2)吨到B地,
由题意可得y=150x+160 (12﹣x)+40(8﹣x)+80(x﹣2)=30x+2080 (2≤x≤8);
(2)由(1)的函数可知,k=30>0,
因此函数的值随x的增大而增大,
当x=2时,有最小值y=30×2+2080=2140(元),
因此当从甲仓库调运2吨到A地时,运费最低,最低运费为2140元.
24.
解:(1)∵等边△AOB的边长为4,
∴点A的横坐标=OB=2,
设点A的纵坐标为a,
即△AOB的底边OB边上的高为a,
∴由勾股定理得,
,
∴点A的坐标为(2,).
(2)将A(2,)代入直线=中,
得,
解得k=,
∴.
(3)将y=0代入中,
解得x=8,
∴点C的坐标为(8,0),
∴OC=8,BC=OC﹣OB=4,
S△ABC=,
∵P在直线AC上,
∴,
即△BPC的高=n=,
∴S△BPC==,
∴S=S△ABC﹣S△BPC
=,
又∵P不与A、C重合,
∴2<m<8.
25.
(1)解:如图①中,连接PC.
∵四边形ABCD是正方形,
∴AB=BC=AD=CD=4,∠CDP=90°,∠ABM=∠CBM=45°,
∵P是AD的中点,
∴PA=PD=2,
∴PC===2,
∵BA=BC,∠ABM=∠CBM,BM=BM,
∴△ABM≌△CBM(SAS),
∴AM=CM,
∴AM+PM=CM+PM,
∵PM+CM≥PC,
∴AM+PM≥2,
∴AM+PM的最小值为2.
故答案为:2.
(2)证明:由旋转的性质可知BM=BN,
∵∠MBN=60°,
∴△BMN是等边三角形.
(3)解:如图②中,过点E作EP⊥x轴于P,连接EC.
由性质可知,AM=EN,
∵△BMN是等边三角形,
∴BM=MN,
∴AM+BM+CM=EN+NM+MC,
∵EN+NM+MC≥EC,
∴E,N,M,C共线时,AM+BM+CM的值最小,此时点M在EC与BD的交点处,
∵AB=BE=4,∠ABE=60°,
∴∠EBP=90°﹣60°=30°,
∴EP=BE=2,PB=PE=2,
∴E(﹣2,2),
∵C(4,0),D(4,4),
设直线EC速度解析式为y=kx+b,则有,
解得,
∴y=(﹣2)x+8﹣4,
同法可得直线BD的解析式为y=x,
由,解得,
∴M(,).
一、选择题(本题共12小题,在每小题给出的四个选项中,只有一个是正确的,请把正确的选项选出来,每小题选对得3分,满分36分.多选、不选、错选均记零分.)
1.下列图形中,既是中心对称图形又是轴对称图形的是( )
A. B.
C. D.
2.下列计算正确的是( )
A. B. C. D.
3.若x>y,且(a﹣3)x<(a﹣3)y,则a的值可能是( )
A.5 B.4 C.3 D.0
4.若最简二次根式是同类二次根式,则x的值为( )
A. B. C.x=1 D.x=﹣1
5.如图,小方格都是边长为1的正方形,则△ABC中BC边上的高等于( )
A.2 B. C.2 D.
6.如图,已知直线y=3x+b与y=ax﹣2的交点的横坐标为﹣2,根据图象有下列3个结论:①a>0;②b<0;③x>﹣2是不等式3x+b>ax﹣2的解集.其中正确的个数是( )
A.0 B.1 C.2 D.3
7.已知A(1,﹣3),B(2,2),现将线段AB平移至CD,如果点A的对应点C的坐标为(﹣3,﹣1),点B的对应点D的坐标为(c,d),那么dc等于( )
A.﹣16 B. C.16 D.0
8.小明要从甲地到乙地,两地相距2千米.已知小明步行的平均速度为100米/分,跑步的平均速度为200米/分,若要在不超过15分钟的时间内到达乙地,至少需要跑步多少分钟?设小明需要跑步x分钟,根据题意可列不等式为( )
A.200x+100(15﹣x)≥2000 B.200x+100(15﹣x)≤2000
C.200x+100(15﹣x)≥2 D.100x+200(15﹣x)≥2
9.甲、乙两人按相同路线前往距离10km的培训中心参加学习,图中l1、l2分别表示甲、乙两人前往目的地所走的路程S(km)随时间t(分)变化的函数图象,以下说法:①甲比乙提前12分钟到达;②甲的平均速度为千米/小时;③甲乙相遇时,乙走了6千米;④乙出发6分钟后追上甲.其中正确的有( )
A.4个 B.3个 C.2个 D.1个
10.如图,将△ABC绕点C(0,1)旋转180°得到△A'B'C',设点A的坐标为(﹣2,3),则点A'的坐标为( )
A.(2,﹣3) B.(﹣1,2) C.(2,﹣2) D.(2,﹣1)
11.设直线y=kx+6与y=(k+1)x+6(k是正整数)及x轴围成的三角形面积为Sk(k=1,2,3,…),则S5的值等于( )
A. B. C.1 D.3
12.如图是一个无理数生成器的工作流程图,根据该流程图,下列说法:
①当输出值y为时,输入值x为5或25;
②当输入值为64时,输出值y为;
③对于任意的正无理数y,都存在正整数x,使得输入x后能够输出y;
④存在这样的正整数x,输入x之后,该生成器能够一直运行,但始终不能输出y值.
其中错误的有( )
A.4个 B.3个 C.2个 D.1个.
二、填空题(本题共6小题,将每小题的最后结果填写在横线上.每小题3分,满分18分)
13.如图,在△ABC中,∠ACB=90°,以它的三边为边分别向外作正方形,面积分别为S1,S2,S3,已知S1=5,S2=12,则S3= .
14.一次函数y=(m+1)x+2m﹣1的图象不经过第二象限,则m的取值范围是 .
15.如图,△OAB绕点O顺时针旋转42°得到△ODC,点D恰好落在AB上,且∠AOC=108°,则∠B度数是 .
16.已知,则代数式的值等于 .
17.已知关于x的不等式组的整数解共有5个,则a的取值范围是 .
18.已知线段EF两个端点的坐标为E(x1,y1),F(x2,y2),若点M(x0,y0)是线段EF的中点,则有x0=.在平面直角坐标系中有三个点A(1,﹣1)、B(﹣1,﹣1)、C(0,1),点P(0,2)关于点A的对称点记为P1,P1关于点B的对称点记为P2,P2关于点C的对称点记为P3,…,按此规律继续以A、B、C三点为对称中心,重复前面的操作,依次得到点P4,P5,P6,…,则点P2020的坐标是 .
三、解答题(本题共7小题,共66分.解答应写出文字说明、证明过程或推演步骤.)
19.(10分)(1)解不等式2(x+8)>3(x﹣2)+1,并把它的解集在数轴上表示出来;
(2)解不等式组:.
20.(8分)计算
(1);
(2).
21.(8分)如图,在每个小正方形边长为1的方格纸中,A点和B点的坐标分别为(2,﹣4)和(﹣2,2),连接AB、BC和CA得到△ABC.
(1)请在图中画出坐标轴建立直角坐标系;
(2)写出点C的坐标为 ;
(3)在y轴上有点D满足S△DBC=S△ABC,则点D的坐标为 ;
(4)作图:在图中作出△ABC关于点E(﹣1,﹣1)成中心对称的图形(保留作图痕迹,不写作法).
22.(8分)如图,在四边形ABCD中,BD是对角线,已知∠ADB=∠CBD,AB=x+3,BD=8,BC=6,CD=10,AD=13﹣x.
求证:四边形ABCD是平行四边形.
23.(10分)预防新型冠状病毒期间,某种消毒液A地需要8吨,B地需要10吨,正好甲仓库储备有12吨,乙仓库储备有6吨.市预防新型冠状病毒领导小组决定将这18吨消毒液调往A地和B地,消毒液的运费价格如表(单位:元/吨),设从甲仓库调运x吨到A地.
终点起点 A地 B地
甲仓库 150 160
乙仓库 40 80
(1)求调运18吨消毒液的总运费y关于x的函数表达式并求出x的取值范围;
(2)求出总运费最低的调运方案,最低运费为多少?
24.(10分)如图,△AOB是边长为4的等边三角形,过点A的直线与x轴交于点C.
(1)求点A的坐标;
(2)求直线AC的函数表达式;
(3)若点P(m,n)是线段AC上的动点(不与A、C重合),设△ABP的面积为S,求S关于m的函数表达式及m的取值范围.
25.(12分)如图①,四边形ABCD是边长为4的正方形,M是正方形对角线BD(不含B、D两个端点)上任意一点,将△BAM绕点B逆时针旋转60°得到△BEN,连接EA、MN;P是AD的中点,连接PM.
(1)AM+PM的最小值等于 ;
(2)求证:△BNM是等边三角形;
(3)如图②,以B为坐标原点建立平面直角坐标系,若点M使得AM+BM+CM的值最小,求M点的坐标.
参考答案
一、选择题(本题共12小题,在每小题给出的四个选项中,只有一个是正确的,请把正确的选项选出来,每小题选对得3分,满分36分.多选、不选、错选均记零分.)
1. A.
2. D.
3. D.
4. C.
5. B.
6. C.
7. B.
8. A.
9. C.
10. D.
11. A.
12. B.
二、填空题(本题共6小题,将每小题的最后结果填写在横线上.每小题3分,满分18分)
13. 17.
14.﹣1<m≤.
15. 45°.
16. 5.
17.﹣3<a≤﹣2.
18.(﹣2,﹣2).
三、解答题(本题共7小题,共66分.解答应写出文字说明、证明过程或推演步骤.)
19.
解:(1)去括号,得:2x+16>3x﹣6+1,
移项,得:2x﹣3x>﹣6+1﹣16,
合并同类项,得:﹣x>﹣21,
系数化为1,得:x<21,
表示在数轴上如下:
(2)解不等式①得:x≤2,
解不等式②得:x>﹣1,
则不等式组的解集为﹣1<x≤2.
20.
解:(1)原式=﹣4+15﹣3﹣4+2
=6;
(2)原式=×2+×5﹣5×2﹣5×5
=6+10﹣10﹣25
=﹣19.
21.
解:(1)平面直角坐标系如图所示.
(2)C(3,2),
故答案为:(3,2).
(3)设D(0,m),则有×5×|2﹣m|×5=×5×6,
解得m=﹣4或8,
∴满足条件的点D的坐标为(0,﹣4)或(0,8),
故答案为:(0,﹣4)或(0,8).
(4)如图,△A′B′C′即为所求.
22.
证明:∵BD=8,BC=6,CD=10,
∴BD2+BC2=CD2,
∴△BCD是直角三角形,∠CBD=90°,
∵∠ADB=∠CBD,
∴AD∥BC,∠ADB=90°,
∴AD2+BD2=AB2,
即(13﹣x)2+82=(x+3)2,
解得:x=7,
∴AD=6,
∴AD=BC,
又∵AD∥BC,
∴四边形ABCD是平行四边形.
23.
解:(1)设从甲仓库调运x吨到A地,则从甲仓库调运(12﹣x)吨到B地,从乙仓库调运(8﹣x)吨到A地,从乙仓库调运10﹣(12﹣x)=(x﹣2)吨到B地,
由题意可得y=150x+160 (12﹣x)+40(8﹣x)+80(x﹣2)=30x+2080 (2≤x≤8);
(2)由(1)的函数可知,k=30>0,
因此函数的值随x的增大而增大,
当x=2时,有最小值y=30×2+2080=2140(元),
因此当从甲仓库调运2吨到A地时,运费最低,最低运费为2140元.
24.
解:(1)∵等边△AOB的边长为4,
∴点A的横坐标=OB=2,
设点A的纵坐标为a,
即△AOB的底边OB边上的高为a,
∴由勾股定理得,
,
∴点A的坐标为(2,).
(2)将A(2,)代入直线=中,
得,
解得k=,
∴.
(3)将y=0代入中,
解得x=8,
∴点C的坐标为(8,0),
∴OC=8,BC=OC﹣OB=4,
S△ABC=,
∵P在直线AC上,
∴,
即△BPC的高=n=,
∴S△BPC==,
∴S=S△ABC﹣S△BPC
=,
又∵P不与A、C重合,
∴2<m<8.
25.
(1)解:如图①中,连接PC.
∵四边形ABCD是正方形,
∴AB=BC=AD=CD=4,∠CDP=90°,∠ABM=∠CBM=45°,
∵P是AD的中点,
∴PA=PD=2,
∴PC===2,
∵BA=BC,∠ABM=∠CBM,BM=BM,
∴△ABM≌△CBM(SAS),
∴AM=CM,
∴AM+PM=CM+PM,
∵PM+CM≥PC,
∴AM+PM≥2,
∴AM+PM的最小值为2.
故答案为:2.
(2)证明:由旋转的性质可知BM=BN,
∵∠MBN=60°,
∴△BMN是等边三角形.
(3)解:如图②中,过点E作EP⊥x轴于P,连接EC.
由性质可知,AM=EN,
∵△BMN是等边三角形,
∴BM=MN,
∴AM+BM+CM=EN+NM+MC,
∵EN+NM+MC≥EC,
∴E,N,M,C共线时,AM+BM+CM的值最小,此时点M在EC与BD的交点处,
∵AB=BE=4,∠ABE=60°,
∴∠EBP=90°﹣60°=30°,
∴EP=BE=2,PB=PE=2,
∴E(﹣2,2),
∵C(4,0),D(4,4),
设直线EC速度解析式为y=kx+b,则有,
解得,
∴y=(﹣2)x+8﹣4,
同法可得直线BD的解析式为y=x,
由,解得,
∴M(,).
同课章节目录
