简单几何体课件
图片预览









文档简介
(共37张PPT)
2011—2012学年提高班课件
第一讲:空间几何体的结构、三视图和直观图
一般地,我们把由若干个平面多边形围成的几何体叫做多面体。围成多面体的各个多边形叫做多面体的面,相邻两个多边形的公共边叫做多面体的棱,棱与棱的公共顶点叫做多面体的顶点。
面
顶点
棱
由若干个平面多边形围成的几何体叫做多面体 .
轴
由一个平面图形绕它所在平面内的一条定直线旋转所形成的封闭几何体叫做旋转体
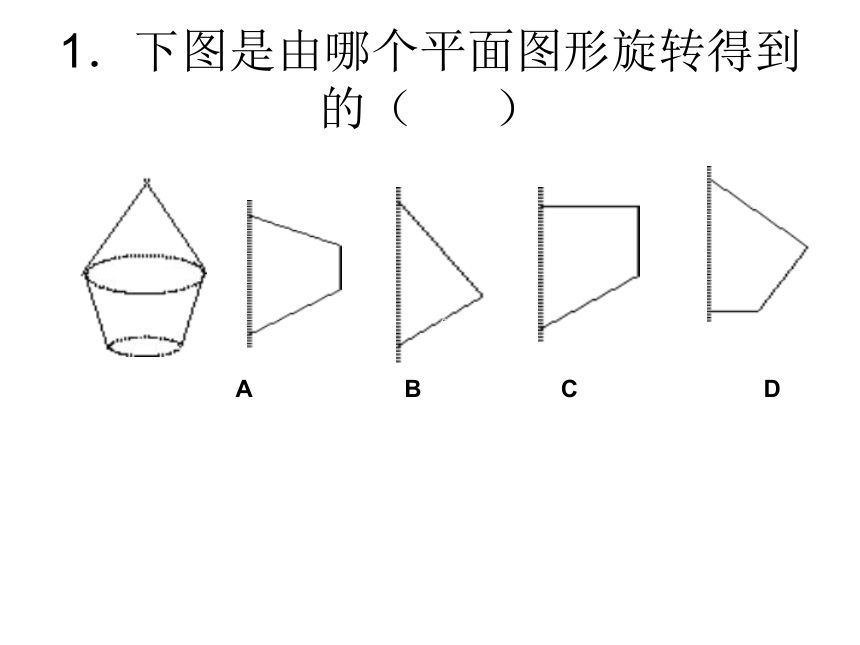
1.下图是由哪个平面图形旋转得到的( )
A B C D
1.下图是由哪个平面图形旋转得到的( )
A B C D
A B C D
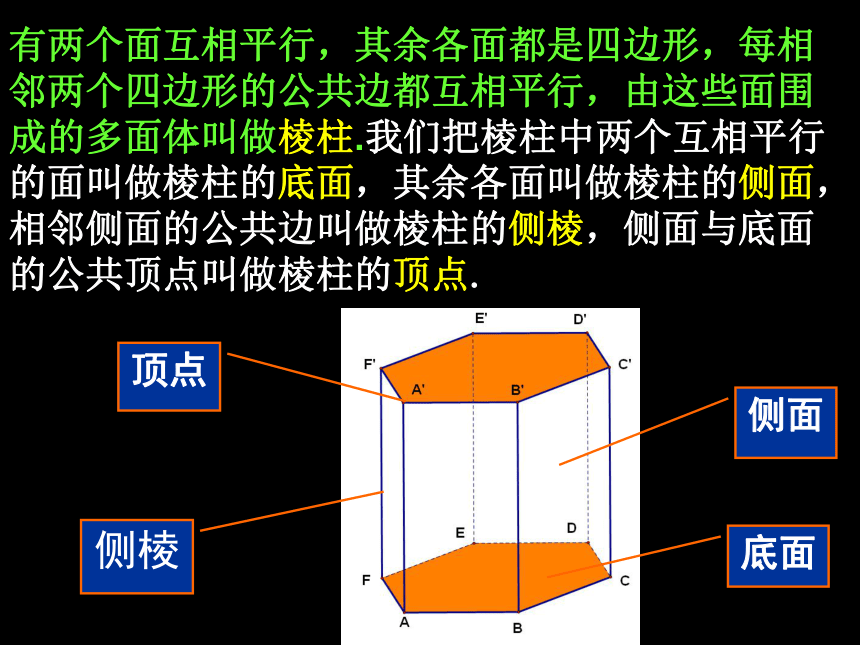
有两个面互相平行,其余各面都是四边形,每相邻两个四边形的公共边都互相平行,由这些面围成的多面体叫做棱柱.我们把棱柱中两个互相平行的面叫做棱柱的底面,其余各面叫做棱柱的侧面,相邻侧面的公共边叫做棱柱的侧棱,侧面与底面的公共顶点叫做棱柱的顶点.
侧面
顶点
侧棱
底面
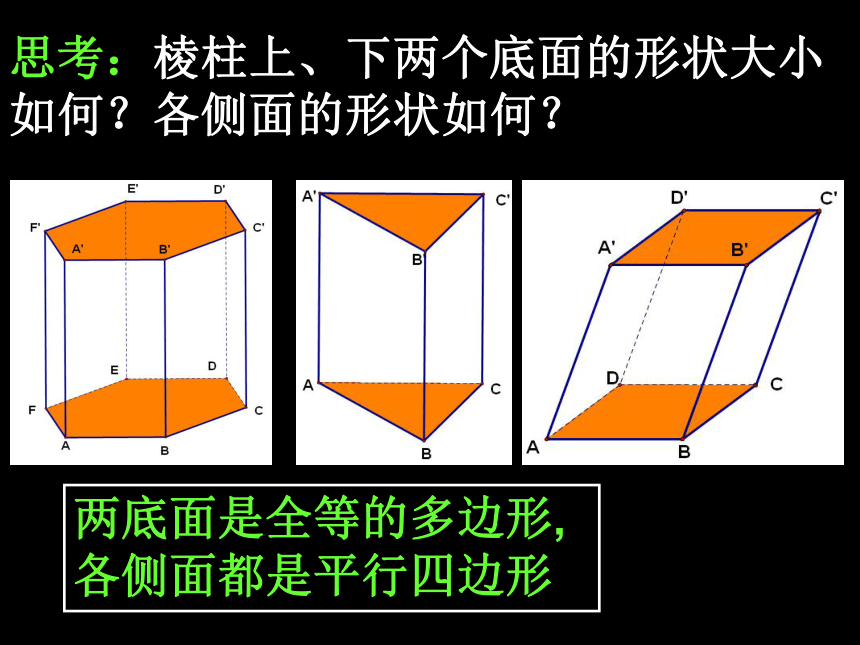
思考:棱柱上、下两个底面的形状大小如何?各侧面的形状如何?
两底面是全等的多边形,各侧面都是平行四边形
思考:有两个面互相平行,其余各面都是平行四边形的多面体一定是棱柱吗?
思考:一个棱柱至少有几个侧面?一个N棱柱分别有多少个底面和侧面?有多少条侧棱?有多少个顶点?
斜棱柱:侧棱不垂直于底面的棱柱叫做斜棱柱,画斜棱柱时, 一般将侧棱画成不与底面垂直。
直棱柱:侧棱垂直于底面的棱柱叫做直棱柱。
画直棱柱时,应将侧棱画成与底面垂直。
正棱柱:底面是正多边形的直棱柱
叫做正棱柱。
平行六面体:底面是平行四边形的四棱柱
叫做平行六面体.
直平行六面体:侧棱与底面垂直的平行六面体
叫直平行六面体。
棱柱的性质:
1)棱柱的各个侧面都是平行四边形,所有的
侧棱都平行且相等;直棱柱的各个侧面都矩
形;正棱柱的各个侧面都是全等的矩形。
2)棱柱的两个底面与平行于底面的截面是对应边互相平行的全等多边形。
3)过棱柱不相邻的两条侧棱的截面都是平行四边形。
4)直棱柱的侧棱长与高相等;直棱柱的侧面
及经过不相邻的两条侧棱的截面都是矩形。
例:已知集合A={正方体},B={长方体},
C={正四棱柱},D={直四棱柱},
E={棱柱},F={直平行六面体},则( )
A、A B C D F E
B、A C B F D E
C、C A B D F E
D、它们之间不都存在包含关系
.
例:已知长方体的全面积是11,十二条棱长度之和是24,则这个长方体的一条对角线长为 ( )
A. 3 B.4 C.5 D.6
例:有三个命题:
甲:底面是平行四边形的四棱柱是平行六面体;
乙:底面是矩形是平行六面体是长方体;
丙:直四棱柱是直平行六面体;
其中真命题的个数是 ( )
A.0个 B.1个 C.2个 D.3个
棱柱的侧面积公式:
(1)直棱柱的底面周长是c,高是h,那么它的侧面积是S=ch
(2)斜棱柱的侧棱长是l,直截面的周长是 ,那么它的侧面积是S斜棱柱侧= l。
棱柱的体积公式:V=Sh(s为底面积,h为高)
例:设正四棱柱的一条对角线之长为3它的全面积是16,则它的体积是 ( )
A.4 B.8 C. D.4或
有一个面是多边形,其余各面都是有一个公共顶点的三角形,由这些面围成的多面体叫做棱锥.
侧面
顶点
侧棱
底面
多边形面叫做棱锥的底面,有公共顶点的各三角形面叫做棱锥的侧面,相邻侧面的公共边叫做棱锥的侧棱,各侧面的公共顶点叫做棱锥的顶点.
正棱锥
如果一个棱锥的底面是正多边形,并且顶点在底面的射影是底面的中心,这样的棱锥叫做正棱锥。
正棱锥性质 : 正棱锥各侧棱相等,各侧面都是全等的等腰三角形,各等腰三角形底边上的高相等;
正棱锥的高、斜高和斜高在底面内的射影组成一个直角三角形,正棱锥的高、侧棱、侧棱在底面内的射影也组成一个直角三角形。
正棱锥的侧棱与底面所成的角都相等;正棱锥的侧面与底面所成的二面角都相等。
正棱锥的侧面积:如果正棱锥的底面周长为c,斜高为h’,那么它的侧面积是 s=1/2ch
棱锥截面性质定理及推论
定理:如果棱锥被平行于底面的平面所截,那么所得的截面与底面相似,截面面积与底面面积的比等于顶点到截面距离与棱锥高的平方比。
推论1:如果棱锥被平行与底面的平面所截,
则棱锥的侧棱和高被截面分成的线段比相等。
推论2:如果棱锥被平行于底面的平面所截,
则截得的小棱锥与原棱锥的侧面积之比也等于它们对应高的平方比,或它们的底面积之比。
例:正四棱锥底面边长为4,侧棱长为3,则其体积为 .
有两个面是互相平行的相似多边形,其余各面都是梯形,每相邻两个梯形的公共腰的延长线共点.
原棱锥的底面和截面分别叫做棱台的下底面和上底面,其余各面叫做棱台的侧面,相邻侧面的公共边叫做棱台的侧棱,侧面与底面的公共顶点叫做棱台的顶点.
侧面
上底面
侧棱
下底面
顶点
例:下列多面体一定是棱台吗?如何判断?
以矩形的一边所在直线为旋转轴,其余三边旋转形成的面所围成的旋转体.
在圆柱的形成中,旋转轴叫做圆柱的轴,垂直于轴的边旋转而成的圆面叫做圆柱的底面,平行于轴的边旋转而成的曲面叫做圆柱的侧面,平行于轴的边在旋转中的任何位置叫做圆柱侧面的母线.
侧面
轴
母线
底面
母线
如果圆柱的底面半径为r,母线长为l,那么圆柱的表面积公式是:
以直角三角形的一条直角边所在直线为旋转轴,其余两边旋转形成的面所围成的旋转体叫做圆锥
旋转轴叫做圆锥的轴,垂直于轴的边旋转而成的圆面叫做圆锥的底面,斜边旋转而成的曲面叫做圆锥的侧面,斜边在旋转中的任何位置叫做圆锥侧面的母线.
侧面
顶点
母线
底面
母线
轴
用一个平行于圆锥底面的平面去截圆锥,截面与底面之间的部分叫做圆台.
圆台可以由什么平面图形旋转而形成?
与圆柱和圆锥一样,圆台也有轴、底面、侧面、母线,它们的含义分别如何?
侧面
上底面
下底面
母线
轴
以半圆的直径所在直线为旋转轴,半圆面旋转一周形成的旋转体叫做球体,简称球.
半圆的圆心、半径、直径,在球体中分别叫做球的球心、球的半径、球的直径,球的外表面叫做球面.那么球的半径还可怎样理解?
O
直径
半径
球心
球面上的点到球心的距离
设球的半径为R,截面圆半径为r,球心与截面圆圆心的距离为d,则R、r、d三者之间的关系
P
O
Oˊ
R
r
d
2011—2012学年提高班课件
第一讲:空间几何体的结构、三视图和直观图
一般地,我们把由若干个平面多边形围成的几何体叫做多面体。围成多面体的各个多边形叫做多面体的面,相邻两个多边形的公共边叫做多面体的棱,棱与棱的公共顶点叫做多面体的顶点。
面
顶点
棱
由若干个平面多边形围成的几何体叫做多面体 .
轴
由一个平面图形绕它所在平面内的一条定直线旋转所形成的封闭几何体叫做旋转体
1.下图是由哪个平面图形旋转得到的( )
A B C D
1.下图是由哪个平面图形旋转得到的( )
A B C D
A B C D
有两个面互相平行,其余各面都是四边形,每相邻两个四边形的公共边都互相平行,由这些面围成的多面体叫做棱柱.我们把棱柱中两个互相平行的面叫做棱柱的底面,其余各面叫做棱柱的侧面,相邻侧面的公共边叫做棱柱的侧棱,侧面与底面的公共顶点叫做棱柱的顶点.
侧面
顶点
侧棱
底面
思考:棱柱上、下两个底面的形状大小如何?各侧面的形状如何?
两底面是全等的多边形,各侧面都是平行四边形
思考:有两个面互相平行,其余各面都是平行四边形的多面体一定是棱柱吗?
思考:一个棱柱至少有几个侧面?一个N棱柱分别有多少个底面和侧面?有多少条侧棱?有多少个顶点?
斜棱柱:侧棱不垂直于底面的棱柱叫做斜棱柱,画斜棱柱时, 一般将侧棱画成不与底面垂直。
直棱柱:侧棱垂直于底面的棱柱叫做直棱柱。
画直棱柱时,应将侧棱画成与底面垂直。
正棱柱:底面是正多边形的直棱柱
叫做正棱柱。
平行六面体:底面是平行四边形的四棱柱
叫做平行六面体.
直平行六面体:侧棱与底面垂直的平行六面体
叫直平行六面体。
棱柱的性质:
1)棱柱的各个侧面都是平行四边形,所有的
侧棱都平行且相等;直棱柱的各个侧面都矩
形;正棱柱的各个侧面都是全等的矩形。
2)棱柱的两个底面与平行于底面的截面是对应边互相平行的全等多边形。
3)过棱柱不相邻的两条侧棱的截面都是平行四边形。
4)直棱柱的侧棱长与高相等;直棱柱的侧面
及经过不相邻的两条侧棱的截面都是矩形。
例:已知集合A={正方体},B={长方体},
C={正四棱柱},D={直四棱柱},
E={棱柱},F={直平行六面体},则( )
A、A B C D F E
B、A C B F D E
C、C A B D F E
D、它们之间不都存在包含关系
.
例:已知长方体的全面积是11,十二条棱长度之和是24,则这个长方体的一条对角线长为 ( )
A. 3 B.4 C.5 D.6
例:有三个命题:
甲:底面是平行四边形的四棱柱是平行六面体;
乙:底面是矩形是平行六面体是长方体;
丙:直四棱柱是直平行六面体;
其中真命题的个数是 ( )
A.0个 B.1个 C.2个 D.3个
棱柱的侧面积公式:
(1)直棱柱的底面周长是c,高是h,那么它的侧面积是S=ch
(2)斜棱柱的侧棱长是l,直截面的周长是 ,那么它的侧面积是S斜棱柱侧= l。
棱柱的体积公式:V=Sh(s为底面积,h为高)
例:设正四棱柱的一条对角线之长为3它的全面积是16,则它的体积是 ( )
A.4 B.8 C. D.4或
有一个面是多边形,其余各面都是有一个公共顶点的三角形,由这些面围成的多面体叫做棱锥.
侧面
顶点
侧棱
底面
多边形面叫做棱锥的底面,有公共顶点的各三角形面叫做棱锥的侧面,相邻侧面的公共边叫做棱锥的侧棱,各侧面的公共顶点叫做棱锥的顶点.
正棱锥
如果一个棱锥的底面是正多边形,并且顶点在底面的射影是底面的中心,这样的棱锥叫做正棱锥。
正棱锥性质 : 正棱锥各侧棱相等,各侧面都是全等的等腰三角形,各等腰三角形底边上的高相等;
正棱锥的高、斜高和斜高在底面内的射影组成一个直角三角形,正棱锥的高、侧棱、侧棱在底面内的射影也组成一个直角三角形。
正棱锥的侧棱与底面所成的角都相等;正棱锥的侧面与底面所成的二面角都相等。
正棱锥的侧面积:如果正棱锥的底面周长为c,斜高为h’,那么它的侧面积是 s=1/2ch
棱锥截面性质定理及推论
定理:如果棱锥被平行于底面的平面所截,那么所得的截面与底面相似,截面面积与底面面积的比等于顶点到截面距离与棱锥高的平方比。
推论1:如果棱锥被平行与底面的平面所截,
则棱锥的侧棱和高被截面分成的线段比相等。
推论2:如果棱锥被平行于底面的平面所截,
则截得的小棱锥与原棱锥的侧面积之比也等于它们对应高的平方比,或它们的底面积之比。
例:正四棱锥底面边长为4,侧棱长为3,则其体积为 .
有两个面是互相平行的相似多边形,其余各面都是梯形,每相邻两个梯形的公共腰的延长线共点.
原棱锥的底面和截面分别叫做棱台的下底面和上底面,其余各面叫做棱台的侧面,相邻侧面的公共边叫做棱台的侧棱,侧面与底面的公共顶点叫做棱台的顶点.
侧面
上底面
侧棱
下底面
顶点
例:下列多面体一定是棱台吗?如何判断?
以矩形的一边所在直线为旋转轴,其余三边旋转形成的面所围成的旋转体.
在圆柱的形成中,旋转轴叫做圆柱的轴,垂直于轴的边旋转而成的圆面叫做圆柱的底面,平行于轴的边旋转而成的曲面叫做圆柱的侧面,平行于轴的边在旋转中的任何位置叫做圆柱侧面的母线.
侧面
轴
母线
底面
母线
如果圆柱的底面半径为r,母线长为l,那么圆柱的表面积公式是:
以直角三角形的一条直角边所在直线为旋转轴,其余两边旋转形成的面所围成的旋转体叫做圆锥
旋转轴叫做圆锥的轴,垂直于轴的边旋转而成的圆面叫做圆锥的底面,斜边旋转而成的曲面叫做圆锥的侧面,斜边在旋转中的任何位置叫做圆锥侧面的母线.
侧面
顶点
母线
底面
母线
轴
用一个平行于圆锥底面的平面去截圆锥,截面与底面之间的部分叫做圆台.
圆台可以由什么平面图形旋转而形成?
与圆柱和圆锥一样,圆台也有轴、底面、侧面、母线,它们的含义分别如何?
侧面
上底面
下底面
母线
轴
以半圆的直径所在直线为旋转轴,半圆面旋转一周形成的旋转体叫做球体,简称球.
半圆的圆心、半径、直径,在球体中分别叫做球的球心、球的半径、球的直径,球的外表面叫做球面.那么球的半径还可怎样理解?
O
直径
半径
球心
球面上的点到球心的距离
设球的半径为R,截面圆半径为r,球心与截面圆圆心的距离为d,则R、r、d三者之间的关系
P
O
Oˊ
R
r
d
