直线的极坐标方程
图片预览






文档简介
(共17张PPT)
§1.3.2直线的极坐标方程
答:与直角坐标系里的情况一样,求曲线的极坐标方程就是找出曲线上动点P的坐标 与 之间的关系,然后列出方程 ( , )=0 ,再化简并讨论。
怎样求曲线的极坐标方程?
复习引入:
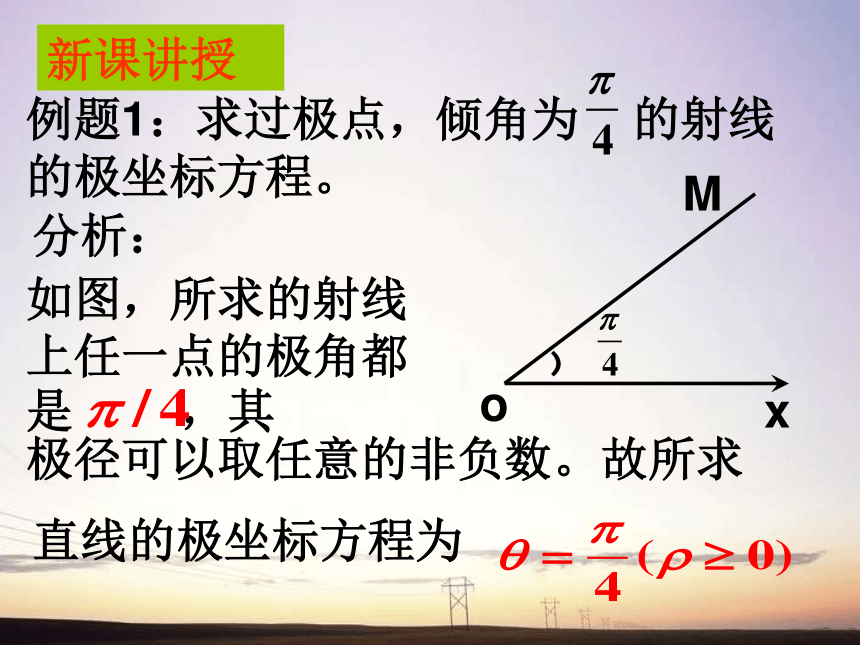
例题1:求过极点,倾角为 的射线的极坐标方程。
o
M
x
﹚
分析:
如图,所求的射线上任一点的极角都是 ,其
极径可以取任意的非负数。故所求
直线的极坐标方程为
新课讲授
1、求过极点,倾角为 的射线的极坐标方程。
易得
思考:
2、求过极点,倾角为 的直线的极坐标方程。
和前面的直角坐标系里直线方程的表示形式比较起来,极坐标系里的直线表示起来很不方便,要用两条射线组合而成。原因在哪?
为了弥补这个不足,可以考虑允许极径可以取全体实数。则上面的直线的极坐标方程可以表示为
或
例题2、求过点A(a,0)(a>0),且垂直于极轴的直线L的极坐标方程。
解:如图,设点
为直线L上除点A外的任意一点,连接OM
o
x
﹚
A
M
在 中有
即
可以验证,点A的坐标也满足上式。
求直线的极坐标方程步骤
1、根据题意画出草图;
2、设点 是直线上任意一点;
3、连接MO;
4、根据几何条件建立关于 的方 程,并化简;
5、检验并确认所得的方程即为所求。
练习:设点P的极坐标为A ,直线 过点P且与极轴所成的角为 ,求直线 的极坐标方程。
解:如图,设点
为直线 上异于的点
连接OM,
﹚
o
M
x
A
在 中有
即
显然A点也满足上方程。
小结:直线的几种极坐标方程
1、过极点
2、过某个定点,且垂直于极轴
3、过某个定点,且与极轴成一定
的角度
O
H
M
A
A、两条相交的直线
B、两条射线
C、一条直线
D、一条射线
( )
B
( )
C
( )
B
O
X
A
B
§1.3.2直线的极坐标方程
答:与直角坐标系里的情况一样,求曲线的极坐标方程就是找出曲线上动点P的坐标 与 之间的关系,然后列出方程 ( , )=0 ,再化简并讨论。
怎样求曲线的极坐标方程?
复习引入:
例题1:求过极点,倾角为 的射线的极坐标方程。
o
M
x
﹚
分析:
如图,所求的射线上任一点的极角都是 ,其
极径可以取任意的非负数。故所求
直线的极坐标方程为
新课讲授
1、求过极点,倾角为 的射线的极坐标方程。
易得
思考:
2、求过极点,倾角为 的直线的极坐标方程。
和前面的直角坐标系里直线方程的表示形式比较起来,极坐标系里的直线表示起来很不方便,要用两条射线组合而成。原因在哪?
为了弥补这个不足,可以考虑允许极径可以取全体实数。则上面的直线的极坐标方程可以表示为
或
例题2、求过点A(a,0)(a>0),且垂直于极轴的直线L的极坐标方程。
解:如图,设点
为直线L上除点A外的任意一点,连接OM
o
x
﹚
A
M
在 中有
即
可以验证,点A的坐标也满足上式。
求直线的极坐标方程步骤
1、根据题意画出草图;
2、设点 是直线上任意一点;
3、连接MO;
4、根据几何条件建立关于 的方 程,并化简;
5、检验并确认所得的方程即为所求。
练习:设点P的极坐标为A ,直线 过点P且与极轴所成的角为 ,求直线 的极坐标方程。
解:如图,设点
为直线 上异于的点
连接OM,
﹚
o
M
x
A
在 中有
即
显然A点也满足上方程。
小结:直线的几种极坐标方程
1、过极点
2、过某个定点,且垂直于极轴
3、过某个定点,且与极轴成一定
的角度
O
H
M
A
A、两条相交的直线
B、两条射线
C、一条直线
D、一条射线
( )
B
( )
C
( )
B
O
X
A
B
