天津市天津一中2020-2021学年高一下学期期末考试数学试题 Word版含答案解析
文档属性
| 名称 | 天津市天津一中2020-2021学年高一下学期期末考试数学试题 Word版含答案解析 |

|
|
| 格式 | docx | ||
| 文件大小 | 804.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-06 00:00:00 | ||
图片预览




文档简介
1126490012420600天津一中2020-2021-2高一年级数学学科期末质量调查试卷
本试卷分为第I卷(选择题)?第II卷(非选择题)两部分,共100分,考试用时90分钟.第Ⅰ卷为第I页,第Ⅱ卷为第2-3页.考生务必将答案涂写规定的位置上,答在试卷上的无效.
祝各位考生考试顺利!
第Ⅰ卷
一、选择题:(每小题4分,共32分)在每小题给出的四个选项中,只有一项是符合题目要求的.
1.复数false满足false,则false( )
A.false B.false C.false D.false
2.已知向量false,且false,则false( )
A.false B.8 C.6 D.false
3.“幸福感指数”是指某个人主观地评价他对自己目前生活状态的满意程度的指标,常用区间[0,10]内的一个数来表示,该数越接近10表示满意度越高.现随机抽取10位和平区居民,他们的幸福感指数为3,4,5,5,6,7,7,8,9,10.则这组数据的80%分位数是( )
A.7.5 B.8 C.8.5 D.9
4.在普通高中新课程改革中,某地实施“3+1+2”选课方案.该方案中“2”指的是从政治?地理?化学?生物4门中任选2门作为选考科目,假设每门科目被选中的可能性相等,那么化学和生物至多有一门被选中的概率是( )
A.false B.false C.false D.false
5.为了给热爱朗读的师生提供一个安静独立的环境,某学校修建了若干"朗读亭".如图所示,该朗读亭的外形是一个正六棱柱和正六棱锥的组合体,正六棱柱两条相对侧棱所在的轴截面为正方形,若正六棱锥与正六棱柱的侧面积之比为false,则正六棱锥与正六棱柱的高的比值为( )
A.false B.false C.false D.false
6.2021年是中国共产党建党100周年,为全面贯彻党的教育方针,提高学生的审美水平和人文素养,促进学生全面发展.某学校高一年级举办了班级合唱活动.现从全校学生中随机抽取部分学生,并邀请他们为此次活动评分(单位:分,满分100分),对评分进行整理,得到如图所示的频率分布直方图,则下列结论不正确的是( )
A.false
B.若该学校有3000名学生参与了评分,则估计评分超过90分的学生人数为600
C.学生评分的众数的估计值为85
D.学生评分的中位数的估计值为83
7.false的内角false的对边分别为false则下列说法正确的个数是( )
①若false,则false
②若false,则false有两解
③若false为钝角三角形,则false
④若false,则false面积的最大值为false
A.1个 B.2个 C.3个 D.4个
8.false中,false为false上一点,false为false上任一点,若false,则false的最小值是( )
A.9 B.10 C.11 D.12
第Ⅱ卷
二、填空题:(每小题4分,共24分)
9.某高校甲?乙?丙?丁四个专业分别有150,150,400,300名学生.为了解学生的就业倾向,用分层随机抽样的方法从该校这四个专业共抽取40名学生进行调查,应在丙专业抽取的学生人数为________人.
10.某同学进行投篮训练,在甲?乙?丙三个不同的位置投中的概率分别false,该同学站在这三个不同的位置各投篮一次,恰好投中两次的概率为false,则false的值为__________.
11.已知某6个数据的平均数为4,方差为8,现加入2和6两个新数据,此时8个数据的方差为__________.
12.已知边长为4的正方形false中,false与false交于点false,且false分别是线段false和线段false的中点,则false__________.
13.如图在三棱锥false中,false分别是false的中点,则异面直线false与false所成角的余弦值为__________.
14.如图三棱锥false,平面false平面false,已知false是等腰三角形,false是等腰直角三角形,若false,球false是三棱锥false的外接球,则球false的表面积是__________.
三.解答题:(本大题共4小题,共44分.解答应写出文字说明,证明过程或演算步骤.)
15.在false中,角false的对边分别为false,已知false
(1)求false的值;
(2)若false,求false的面积false.
16.如图,在四棱锥false中,底面四边形false满足false,false,且false为false的中点.
(1)求证:false平面false;
(2)若平面false平面false,且false,求证:平面false平面false.
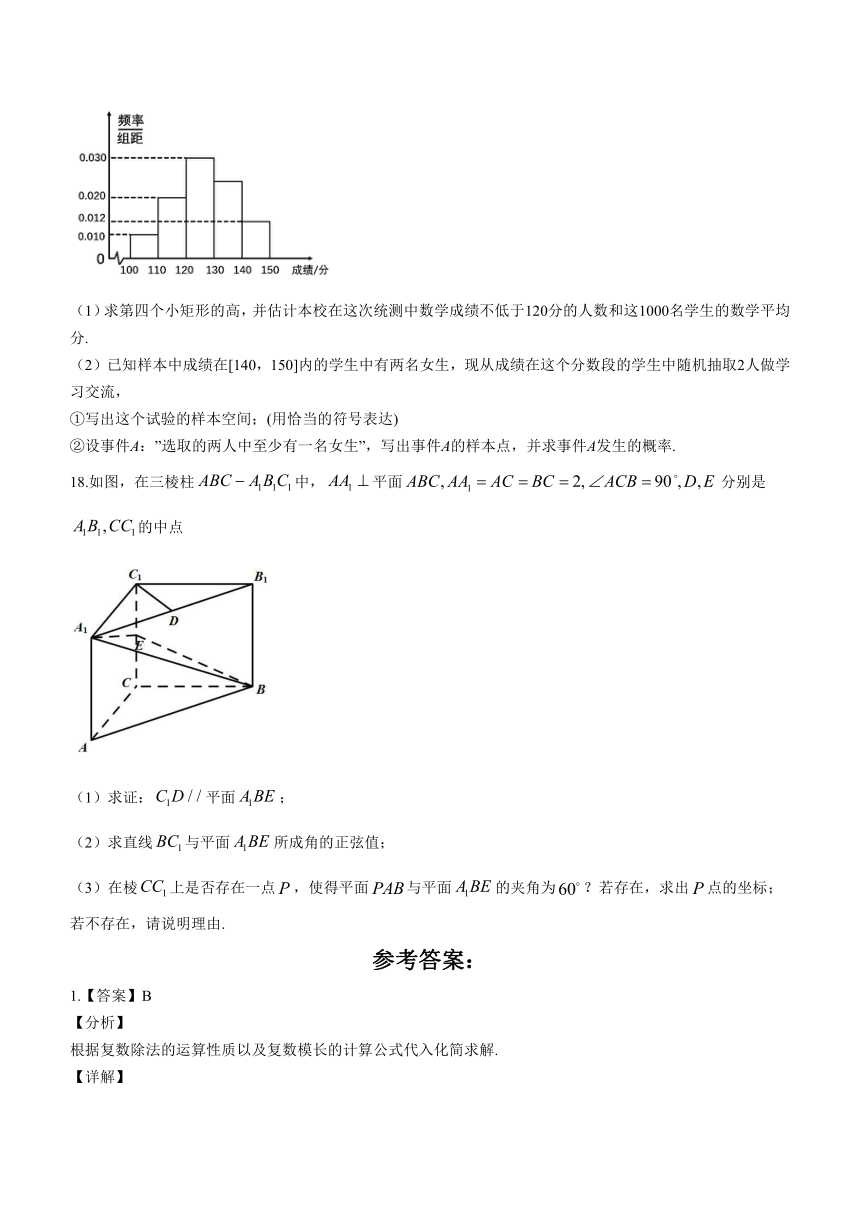
17.天津市某中学高三年级有1000名学生参加学情调研测试,用简单随机抽样的方法抽取了一个容量为50的样本,得到数学成绩的频率分布直方图如图所示:
(1)求第四个小矩形的高,并估计本校在这次统测中数学成绩不低于120分的人数和这1000名学生的数学平均分.
(2)已知样本中成绩在[140,150]内的学生中有两名女生,现从成绩在这个分数段的学生中随机抽取2人做学习交流,
①写出这个试验的样本空间;(用恰当的符号表达)
②设事件A:”选取的两人中至少有一名女生”,写出事件A的样本点,并求事件A发生的概率.
18.如图,在三棱柱false中,false平面false分别是false的中点
(1)求证:false平面false;
(2)求直线false与平面false所成角的正弦值;
(3)在棱false上是否存在一点false,使得平面false与平面false的夹角为false?若存在,求出false点的坐标;若不存在,请说明理由.
参考答案:
1.【答案】B
【分析】
根据复数除法的运算性质以及复数模长的计算公式代入化简求解.
【详解】
由题意,false,则
false
故选:B.
2.【答案】B
【解析】
因为向量false,所以false,
又false,所以false,所以false.故选B.
3.C
4.【答案】D
【分析】
采用列举法得到所有可能的情况,根据古典概型概率计算公式得到结果.
【详解】
从4门学科中任选2门共有:政治+地理?政治+化学?
政治+生物?地理+化学?地理+生物?化学+生物,共6种情况,
其中满足化学和生物至少有一门被选中的有5种情况,所以其概率为false.
故选:D
5.【答案】D
【解析】设正六棱柱底面边长为a,由题意可知正六棱柱的高为2a,
则可知正六棱柱的侧面积为false.
设正六棱锥的高为false,可知正六棱锥侧面的一个三角形的边为false上的高为false,
所以正六棱锥的侧面积为false,
由题意有false,所以六棱锥与正六棱柱的高的比值为false.
故选D.
6.【答案】D
【分析】
对A,由频率之和为1可得;对B,根据频率分布直方图直接计算;对C,由最高长方形底边中点对应的横坐标是样本数据的众数可得;对D,先判断出中位数在false内,列出式子可求.
【详解】
对于A,由频率分布直方图中各个小矩形的面积之和为1,知
false,解得false,A正确;
对于B,由频率分布直方图易知,估计参与评分的3000名学生中,评分超过90分的人数
为false,B正确;
对于C,由频率分布直方图可知,众数的估计值为85,C正确;
对于D,前三组频率之和为false,前四组频率之和为
false,则中位数在false内,
设学生评分的中位数的估计值为x,则false,解得false,D错误.
故选:D.
【点睛】
频率分布直方图中的常用结论:(1)频率分布直方图中所有小长方形的面积之和为1;(2)频率分布直方图中最高长方形底边中点对应的横坐标是样本数据的众数;(3)平分频率分布直方图中小矩形的面积且垂直于横轴的直线与横轴交点的横坐标是样本数据的中位数;(4)频率分布直方图中每个小长方形的面积与对应小长方形底边中点的横坐标的乘积之和是样本数据的平均数.
7.【答案】C
【分析】
利用正弦定理结合大边对大角定理可判断A选项的正误;利用正弦定理可判断B选项的正误;利用余弦定理可判断C选项的正误;利用基本不等式?余弦定理结合三角形的面积公式可判断D选项的正误.
【详解】
对于false选项,若false,则false,由正弦定理可得false,所以,false选项正确;
对于B选项,false,则false,所以,false有两解,false选项
正确;
对于false选项,若false为钝角三角形且false为钝角,则false,可得
false选项错误
对于D选项,由余弦定理与基本不等式可得
false,
即false,当且仅当false时,等号成立,
所以,false,D选项正确.
故选:C.
【点睛】
方法点睛:求三角形面积的最值是一种常见的类型,主要方法有两类:
(1)找到边与边之间的关系,利用基本不等式来求解;
(2)利用正弦定理,转化为关于某个角的三角函数,利用函数思想求解.
8.【答案】D
【分析】
由题意结合向量共线的充分必要条件首先确定m,n的关系,然后结合均值不等式的结论整理计算即可求得最终结果.
【详解】
由题意可知false,
false三点共线,则false,据此有:false
当且仅当false时等号成立.综上可得false的最小值是12
本题选择false选项.
9.【答案】16
【解析】因为高校甲乙丙丁四个专业分别有150,150,400,300名学生,所以本校共有学生
1000名,因为用分层抽样的方法从该校四个专业共抽取40名学生进行调查,所以每个个
体被抽到的概率是false,因为丙专业有400人,所以要抽取false人.
10.【答案】false
【分析】在甲?乙?丙处投中分别记为事件false,恰好投中两次为事件false,false发生,由此利用相互独立事件概率乘法公式能求出结果.
【详解】
在甲?乙?丙处投中分别记为事件false,
恰好投中两次为事件false发生,
故恰好投中两次的概率false,
解得false.
故答案为false
【点睛】
本题考查概率的求法,考查相互独立事件概率乘法公式等基础知识,考查运算求解能力,是基础题.
11.【答案】false
【分析】
利用方差公式可求得结果.
【详解】
设原数据为false,则false
加入2和6两个新数据后,所得8个数据的平均数为false,
所得8个数据的方差为false.
故选:false.
12.【答案】false
以false为坐标原点,false所在直线为false轴建系,
则false
false
13.false
14.C
15.【答案】(1)false;(2)false.
【解析】
【分析】(1)在false中,由正弦定理化简得false,又
由false,化简得false,即可求得false的值;
(2)在false中,由余弦定理,列出关于false方程,求得false,再利用三角形的面积公式,即可求解
【详解】
(1)由题意,知false,
由正弦定理可得false,
整理得false,
即false,
又因为false,则false,所以false,
即false,
又因为false,所以false,解得false.
(2)在false中,由余弦定理可得false,
因为false,所以12false,解得false,所以false,
则三角形的面积false.
【点睛】本题主要考查了正弦定理?余弦定理和三角形的面积公式的应用,其中在解有关三角形的题目时,要抓住题设条件和利用某个定理的信息,合理应用正弦定理和余弦定理李额方程求解是解答的关键,着重考查了运算与求解能力,属于基础题.
16.【答案】(1)证明见解析;(2)证明见解析.
【解析】
【分析】(1)取false的中点false,连结false,推导出四边形false是平行四边形,得到false,由线面平行的判定定理,即可证明false平面false.
(2)由面面垂直的性质定理可证false平面false,得到false平面false,由面面垂直的判定定理,可证明平面false平面false.
【详解】证明false(1)取false的中点false,连接false.
因为false是false的中点,
所以false为false的中位线,
所以false.
又因为false/false,
所以false
所以四边形false为平行四边形,
所以false.
又false平面false平面false,
所以false//平面false.
(2)因为平面false平面false,且平面false平面false,
false平面false,所以false平面false.
false平面false.
又因为false为false的中点,所以false,
false平面false平面false,且false,
所以false平面false.
又false平面false,
所以平面false平面false.
【点睛】本题考查线面平行?面面垂直的证明,考查空间中线线?线面?面面间的位置关系等基础知识,考查运算求解能力,是中档题.
17.(1)由频率分布直方图可知,第四个矩形的高为:false,成绩不低于120分的频率为:false;所以高三年级不低于120分的人数为:
false人.
false
false
(2)由频率分布直方图知,成绩在[140,150]的人数是6,记女生为false,B,男生为false,从这6人中抽取2人的情况有false,
false,共15种.其中至少有一名女生的情况有9种,故至少
有一名女生的概率为false.
18.(1)证明:取false的中点false,连接false,交false于点false,可知false为false的中点,
连接false,易知四边形false为平行四边形,所以false,
又false平面false平面false,所以false平面false.
(2)分别以false所在的直线为false轴?false轴,false轴建立如图所示的空间直角坐标系,
可得false,
则false,false,false,
设平面false的法向量为false,
则false,即false,令false,可得false,即false,
所以false,
所以直线false与平面false所成角的正弦值为false.
(3)假设在棱false是存在一点false,设false,可得false,
由false,可得false,false,
设平面false的法向量为false,
则false,即false,令false,可得false,即false,
又由平面false的一个法向量为false,
所以false,
因为平面false与平面false所成二面角为false,
可得false,解得false,
此时false,符合题意,
所以在棱false上存在一点false,使得平面false与平面false所成二面角为false.
本试卷分为第I卷(选择题)?第II卷(非选择题)两部分,共100分,考试用时90分钟.第Ⅰ卷为第I页,第Ⅱ卷为第2-3页.考生务必将答案涂写规定的位置上,答在试卷上的无效.
祝各位考生考试顺利!
第Ⅰ卷
一、选择题:(每小题4分,共32分)在每小题给出的四个选项中,只有一项是符合题目要求的.
1.复数false满足false,则false( )
A.false B.false C.false D.false
2.已知向量false,且false,则false( )
A.false B.8 C.6 D.false
3.“幸福感指数”是指某个人主观地评价他对自己目前生活状态的满意程度的指标,常用区间[0,10]内的一个数来表示,该数越接近10表示满意度越高.现随机抽取10位和平区居民,他们的幸福感指数为3,4,5,5,6,7,7,8,9,10.则这组数据的80%分位数是( )
A.7.5 B.8 C.8.5 D.9
4.在普通高中新课程改革中,某地实施“3+1+2”选课方案.该方案中“2”指的是从政治?地理?化学?生物4门中任选2门作为选考科目,假设每门科目被选中的可能性相等,那么化学和生物至多有一门被选中的概率是( )
A.false B.false C.false D.false
5.为了给热爱朗读的师生提供一个安静独立的环境,某学校修建了若干"朗读亭".如图所示,该朗读亭的外形是一个正六棱柱和正六棱锥的组合体,正六棱柱两条相对侧棱所在的轴截面为正方形,若正六棱锥与正六棱柱的侧面积之比为false,则正六棱锥与正六棱柱的高的比值为( )
A.false B.false C.false D.false
6.2021年是中国共产党建党100周年,为全面贯彻党的教育方针,提高学生的审美水平和人文素养,促进学生全面发展.某学校高一年级举办了班级合唱活动.现从全校学生中随机抽取部分学生,并邀请他们为此次活动评分(单位:分,满分100分),对评分进行整理,得到如图所示的频率分布直方图,则下列结论不正确的是( )
A.false
B.若该学校有3000名学生参与了评分,则估计评分超过90分的学生人数为600
C.学生评分的众数的估计值为85
D.学生评分的中位数的估计值为83
7.false的内角false的对边分别为false则下列说法正确的个数是( )
①若false,则false
②若false,则false有两解
③若false为钝角三角形,则false
④若false,则false面积的最大值为false
A.1个 B.2个 C.3个 D.4个
8.false中,false为false上一点,false为false上任一点,若false,则false的最小值是( )
A.9 B.10 C.11 D.12
第Ⅱ卷
二、填空题:(每小题4分,共24分)
9.某高校甲?乙?丙?丁四个专业分别有150,150,400,300名学生.为了解学生的就业倾向,用分层随机抽样的方法从该校这四个专业共抽取40名学生进行调查,应在丙专业抽取的学生人数为________人.
10.某同学进行投篮训练,在甲?乙?丙三个不同的位置投中的概率分别false,该同学站在这三个不同的位置各投篮一次,恰好投中两次的概率为false,则false的值为__________.
11.已知某6个数据的平均数为4,方差为8,现加入2和6两个新数据,此时8个数据的方差为__________.
12.已知边长为4的正方形false中,false与false交于点false,且false分别是线段false和线段false的中点,则false__________.
13.如图在三棱锥false中,false分别是false的中点,则异面直线false与false所成角的余弦值为__________.
14.如图三棱锥false,平面false平面false,已知false是等腰三角形,false是等腰直角三角形,若false,球false是三棱锥false的外接球,则球false的表面积是__________.
三.解答题:(本大题共4小题,共44分.解答应写出文字说明,证明过程或演算步骤.)
15.在false中,角false的对边分别为false,已知false
(1)求false的值;
(2)若false,求false的面积false.
16.如图,在四棱锥false中,底面四边形false满足false,false,且false为false的中点.
(1)求证:false平面false;
(2)若平面false平面false,且false,求证:平面false平面false.
17.天津市某中学高三年级有1000名学生参加学情调研测试,用简单随机抽样的方法抽取了一个容量为50的样本,得到数学成绩的频率分布直方图如图所示:
(1)求第四个小矩形的高,并估计本校在这次统测中数学成绩不低于120分的人数和这1000名学生的数学平均分.
(2)已知样本中成绩在[140,150]内的学生中有两名女生,现从成绩在这个分数段的学生中随机抽取2人做学习交流,
①写出这个试验的样本空间;(用恰当的符号表达)
②设事件A:”选取的两人中至少有一名女生”,写出事件A的样本点,并求事件A发生的概率.
18.如图,在三棱柱false中,false平面false分别是false的中点
(1)求证:false平面false;
(2)求直线false与平面false所成角的正弦值;
(3)在棱false上是否存在一点false,使得平面false与平面false的夹角为false?若存在,求出false点的坐标;若不存在,请说明理由.
参考答案:
1.【答案】B
【分析】
根据复数除法的运算性质以及复数模长的计算公式代入化简求解.
【详解】
由题意,false,则
false
故选:B.
2.【答案】B
【解析】
因为向量false,所以false,
又false,所以false,所以false.故选B.
3.C
4.【答案】D
【分析】
采用列举法得到所有可能的情况,根据古典概型概率计算公式得到结果.
【详解】
从4门学科中任选2门共有:政治+地理?政治+化学?
政治+生物?地理+化学?地理+生物?化学+生物,共6种情况,
其中满足化学和生物至少有一门被选中的有5种情况,所以其概率为false.
故选:D
5.【答案】D
【解析】设正六棱柱底面边长为a,由题意可知正六棱柱的高为2a,
则可知正六棱柱的侧面积为false.
设正六棱锥的高为false,可知正六棱锥侧面的一个三角形的边为false上的高为false,
所以正六棱锥的侧面积为false,
由题意有false,所以六棱锥与正六棱柱的高的比值为false.
故选D.
6.【答案】D
【分析】
对A,由频率之和为1可得;对B,根据频率分布直方图直接计算;对C,由最高长方形底边中点对应的横坐标是样本数据的众数可得;对D,先判断出中位数在false内,列出式子可求.
【详解】
对于A,由频率分布直方图中各个小矩形的面积之和为1,知
false,解得false,A正确;
对于B,由频率分布直方图易知,估计参与评分的3000名学生中,评分超过90分的人数
为false,B正确;
对于C,由频率分布直方图可知,众数的估计值为85,C正确;
对于D,前三组频率之和为false,前四组频率之和为
false,则中位数在false内,
设学生评分的中位数的估计值为x,则false,解得false,D错误.
故选:D.
【点睛】
频率分布直方图中的常用结论:(1)频率分布直方图中所有小长方形的面积之和为1;(2)频率分布直方图中最高长方形底边中点对应的横坐标是样本数据的众数;(3)平分频率分布直方图中小矩形的面积且垂直于横轴的直线与横轴交点的横坐标是样本数据的中位数;(4)频率分布直方图中每个小长方形的面积与对应小长方形底边中点的横坐标的乘积之和是样本数据的平均数.
7.【答案】C
【分析】
利用正弦定理结合大边对大角定理可判断A选项的正误;利用正弦定理可判断B选项的正误;利用余弦定理可判断C选项的正误;利用基本不等式?余弦定理结合三角形的面积公式可判断D选项的正误.
【详解】
对于false选项,若false,则false,由正弦定理可得false,所以,false选项正确;
对于B选项,false,则false,所以,false有两解,false选项
正确;
对于false选项,若false为钝角三角形且false为钝角,则false,可得
false选项错误
对于D选项,由余弦定理与基本不等式可得
false,
即false,当且仅当false时,等号成立,
所以,false,D选项正确.
故选:C.
【点睛】
方法点睛:求三角形面积的最值是一种常见的类型,主要方法有两类:
(1)找到边与边之间的关系,利用基本不等式来求解;
(2)利用正弦定理,转化为关于某个角的三角函数,利用函数思想求解.
8.【答案】D
【分析】
由题意结合向量共线的充分必要条件首先确定m,n的关系,然后结合均值不等式的结论整理计算即可求得最终结果.
【详解】
由题意可知false,
false三点共线,则false,据此有:false
当且仅当false时等号成立.综上可得false的最小值是12
本题选择false选项.
9.【答案】16
【解析】因为高校甲乙丙丁四个专业分别有150,150,400,300名学生,所以本校共有学生
1000名,因为用分层抽样的方法从该校四个专业共抽取40名学生进行调查,所以每个个
体被抽到的概率是false,因为丙专业有400人,所以要抽取false人.
10.【答案】false
【分析】在甲?乙?丙处投中分别记为事件false,恰好投中两次为事件false,false发生,由此利用相互独立事件概率乘法公式能求出结果.
【详解】
在甲?乙?丙处投中分别记为事件false,
恰好投中两次为事件false发生,
故恰好投中两次的概率false,
解得false.
故答案为false
【点睛】
本题考查概率的求法,考查相互独立事件概率乘法公式等基础知识,考查运算求解能力,是基础题.
11.【答案】false
【分析】
利用方差公式可求得结果.
【详解】
设原数据为false,则false
加入2和6两个新数据后,所得8个数据的平均数为false,
所得8个数据的方差为false.
故选:false.
12.【答案】false
以false为坐标原点,false所在直线为false轴建系,
则false
false
13.false
14.C
15.【答案】(1)false;(2)false.
【解析】
【分析】(1)在false中,由正弦定理化简得false,又
由false,化简得false,即可求得false的值;
(2)在false中,由余弦定理,列出关于false方程,求得false,再利用三角形的面积公式,即可求解
【详解】
(1)由题意,知false,
由正弦定理可得false,
整理得false,
即false,
又因为false,则false,所以false,
即false,
又因为false,所以false,解得false.
(2)在false中,由余弦定理可得false,
因为false,所以12false,解得false,所以false,
则三角形的面积false.
【点睛】本题主要考查了正弦定理?余弦定理和三角形的面积公式的应用,其中在解有关三角形的题目时,要抓住题设条件和利用某个定理的信息,合理应用正弦定理和余弦定理李额方程求解是解答的关键,着重考查了运算与求解能力,属于基础题.
16.【答案】(1)证明见解析;(2)证明见解析.
【解析】
【分析】(1)取false的中点false,连结false,推导出四边形false是平行四边形,得到false,由线面平行的判定定理,即可证明false平面false.
(2)由面面垂直的性质定理可证false平面false,得到false平面false,由面面垂直的判定定理,可证明平面false平面false.
【详解】证明false(1)取false的中点false,连接false.
因为false是false的中点,
所以false为false的中位线,
所以false.
又因为false/false,
所以false
所以四边形false为平行四边形,
所以false.
又false平面false平面false,
所以false//平面false.
(2)因为平面false平面false,且平面false平面false,
false平面false,所以false平面false.
false平面false.
又因为false为false的中点,所以false,
false平面false平面false,且false,
所以false平面false.
又false平面false,
所以平面false平面false.
【点睛】本题考查线面平行?面面垂直的证明,考查空间中线线?线面?面面间的位置关系等基础知识,考查运算求解能力,是中档题.
17.(1)由频率分布直方图可知,第四个矩形的高为:false,成绩不低于120分的频率为:false;所以高三年级不低于120分的人数为:
false人.
false
false
(2)由频率分布直方图知,成绩在[140,150]的人数是6,记女生为false,B,男生为false,从这6人中抽取2人的情况有false,
false,共15种.其中至少有一名女生的情况有9种,故至少
有一名女生的概率为false.
18.(1)证明:取false的中点false,连接false,交false于点false,可知false为false的中点,
连接false,易知四边形false为平行四边形,所以false,
又false平面false平面false,所以false平面false.
(2)分别以false所在的直线为false轴?false轴,false轴建立如图所示的空间直角坐标系,
可得false,
则false,false,false,
设平面false的法向量为false,
则false,即false,令false,可得false,即false,
所以false,
所以直线false与平面false所成角的正弦值为false.
(3)假设在棱false是存在一点false,设false,可得false,
由false,可得false,false,
设平面false的法向量为false,
则false,即false,令false,可得false,即false,
又由平面false的一个法向量为false,
所以false,
因为平面false与平面false所成二面角为false,
可得false,解得false,
此时false,符合题意,
所以在棱false上存在一点false,使得平面false与平面false所成二面角为false.
同课章节目录
