苏科版八年级上册第五章 平面直角坐标系5.2平面直角坐标系课件(29张ppt)
文档属性
| 名称 | 苏科版八年级上册第五章 平面直角坐标系5.2平面直角坐标系课件(29张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-07 06:22:18 | ||
图片预览




文档简介
(共29张PPT)
5.2平面直角坐标系(1)
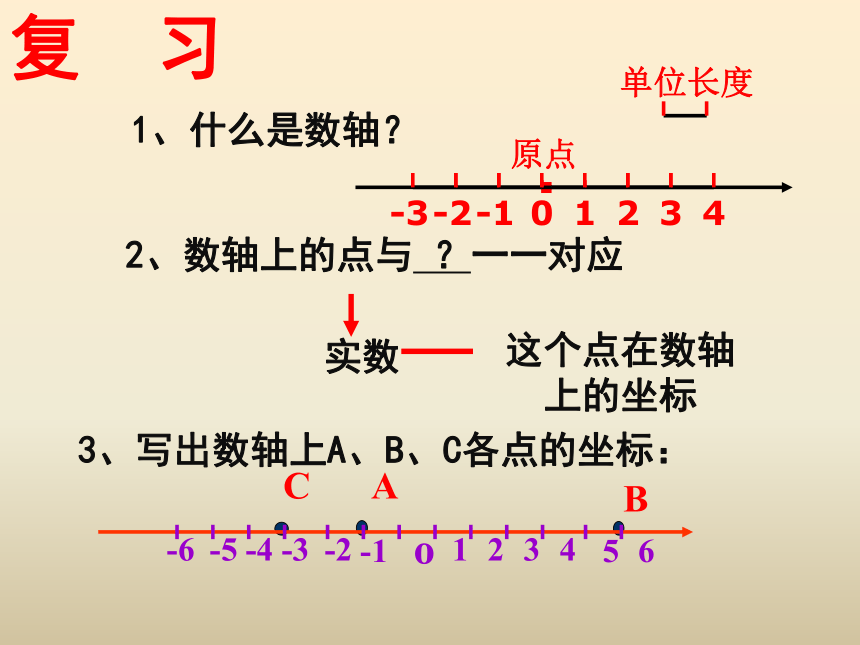
1、什么是数轴?
复 习
·
单位长度
0
1
2
3
4
-3
-2
-1
原点
2、数轴上的点与
?一一对应
实数
这个点在数轴上的坐标
3、写出数轴上A、B、C各点的坐标:
A
B
C
o
1
2
3
4
5
6
-1
-2
-3
-4
-5
-6
4、平面上确定位置的方法
(1)用有序数对法
(2)用方向和距离法
归纳:
平面上确定一个位置一般
需要2个实数。而且两个实数的
意义不同,先后顺序不能调换。
第1列
第2列
第3列
第4列
第5列
第6列
第1行
第2行
第3行
第4行
第5行
第6行
讲台
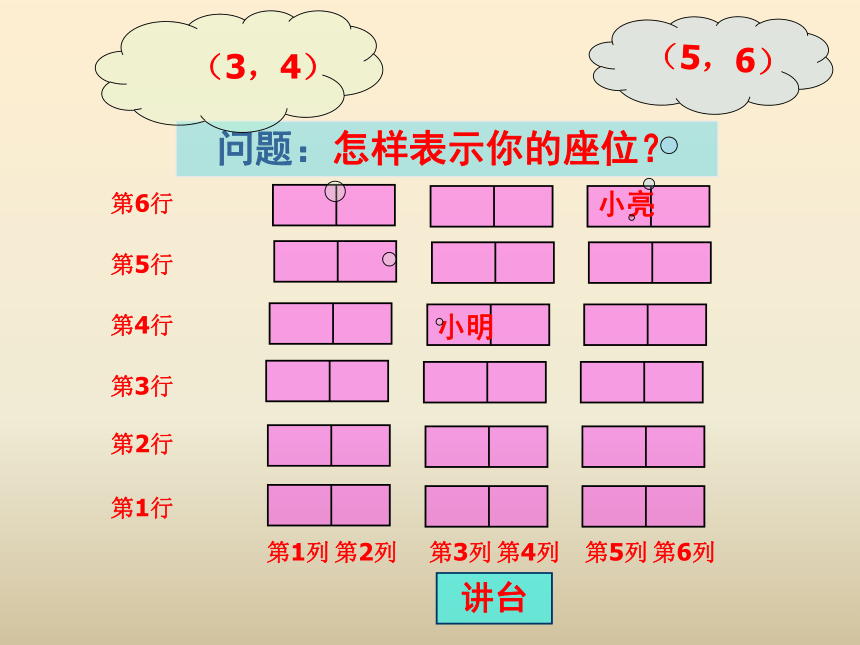
问题:怎样表示你的座位?
小明
小亮
(3,4)
(5,6)
德育路
德育路
锡宅路
锡宅路
双象大酒店
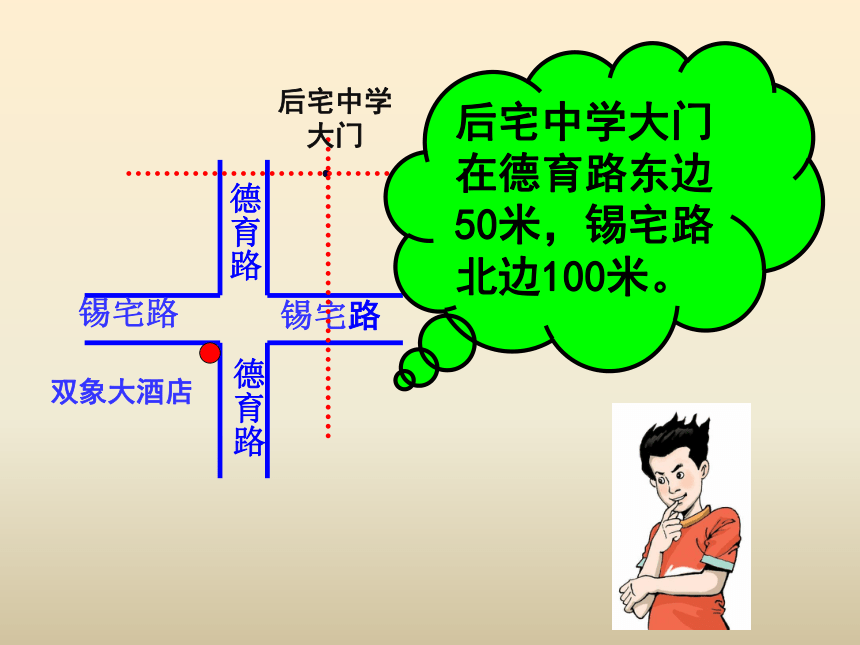
后宅中学大门在德育路东边50米,锡宅路北边100米。
后宅中学大门
1、小明是怎样描述后宅中学大门的位置?
2、小明省去“北边”和“东边”
这几个字可以吗?
3、如果小明仅仅说在“锡宅路北边、德育路东边”,你能找到后宅中学大门吗?
锡宅路
德育路
后宅中学大门
50
100
北
东
4、如果小明只说在“锡宅路北边100米”,或只说在“德育路东边50米”,你能找到后宅中学的大门吗?
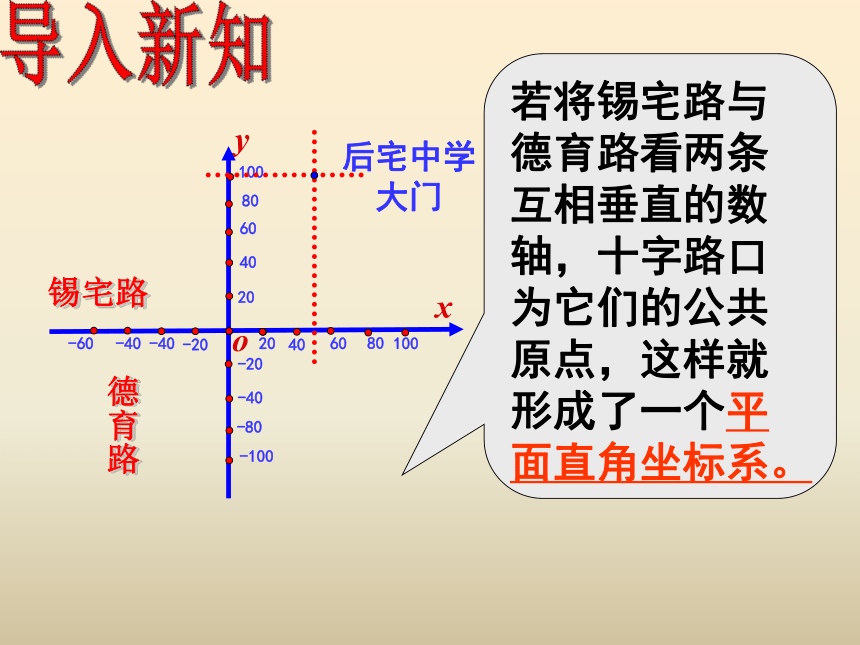
若将锡宅路与德育路看两条互相垂直的数轴,十字路口为它们的公共原点,这样就形成了一个平面直角坐标系。
x
y
o
60
40
20
80
20
-20
-40
-80
-100
40
80
60
-40
-40
-20
-60
100
100
后宅中学大门
锡宅路
德育路
x
y
o
-1
2
3
4
5
6
7
8
9
-2
-3
-4
-5
-6
-7
-8
-9
1
1
2
3
4
5
-1
-2
-3
-4
-5
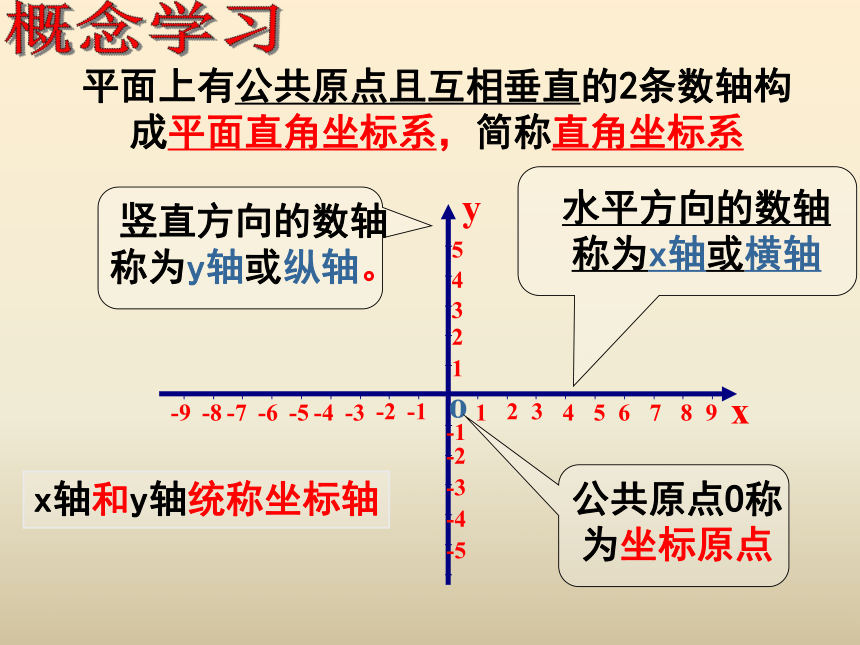
平面上有公共原点且互相垂直的2条数轴构成平面直角坐标系,简称直角坐标系
水平方向的数轴称为x轴或横轴
竖直方向的数轴称为y轴或纵轴。
x轴和y轴统称坐标轴
公共原点O称为坐标原点
解析几何的创始人
──笛卡尔
笛卡尔(1596—1650),法国数学家。
他所创建的直角坐标系标志着代数与几何的第一次完美结合,使形形色色的代数方程表现为不同的几何图形,许多相当难解的几何题转化为代数题后能轻而易举地找到答案。
3
1
4
2
5
-2
-4
-1
-3
o
1
2
3
4
5
-4
-3
-2
-1
x
横轴
y
纵轴
原点
平面直角坐标系具有以下特征:
①两条数轴互相垂直
②原点重合
③通常取向右、向上为正方向
④单位长度一般取相同的
平面直角坐标系
3
1
4
2
5
-2
-4
-1
-3
0
1
2
3
4
5
-4
-3
-2
-1
x
(横轴)
y
(纵轴)
原点
第一象限
第二象限
第三象限
第四象限
两条坐标轴把平面分成四个区域,称为象限
注意:坐标轴是象限与象限之间的分界,因此坐标轴上的点不属于任何象限
-1
0
1
1
-1
Q
即:(m,n)
x
y
过Q点作x轴的垂线,过Q点作y轴的垂线,
已知点Q的位置,如何确定Q的坐标呢?
两垂足对应的数就是点Q的坐标。
m
n
横坐标在前,
纵坐标在后,
中间隔开用逗号
勿忘加括号!
它们的位置
a
过y轴上表示坐标为b的点画y轴的垂线
-1
0
1
1
-1
b
P
x
y
过x轴上表示坐标为a的点画x轴的垂线
这两条垂线的交点即为点P,
(a,b)
已知P的坐标为(a,b),如何确定P的位置呢?
y
o
-1
2
3
4
5
6
7
8
9
-2
-3
-4
-5
-6
-7
-8
-9
1
1
2
3
4
5
-1
-2
-3
-4
-5
A
(3,2)
B
(2,3)
C
D
E
分别在平面内确定点A(3,2)、B(2,3)的位置,并确定点C、D、E的坐标。
x
(-3,3)
(5,-3)
(-7,-5)
坐标平面上的点
一对有序实数
(+,+)
(-,+)
(-,-)
(+,-)
x
y
o
-1
2
3
4
5
6
7
8
9
-2
-3
-4
-5
-6
-7
-8
-9
1
1
2
3
4
5
-1
-2
-3
-4
-5
A
B
C
各象限内的点的坐标有何特征?
D
E
(-2,3)
(5,3)
(3,2)
(5,-4)
(-7,-5)
F
G
H
(-7,2)
(-5,-4)
(3,-5)
A
B
C
D
(3,0)
(-4,0)
(0,5)
(0,-4)
(0,0)
坐标轴上点有何特征?
在x轴上的点,
纵坐标等于0.
在y轴上的点,
横坐标等于0.
A(
3,
2
)
B(
0,-2
)
C(-3,-2)
D(-3,
0
)
E(-1.5,3.5)
F(
2,
-3
)
第一象限
第三象限
第二象限
第四象限
y轴上
x轴上
练一练:
下列各点分别在坐标平面的什么位置上?
本节课我们学面直角坐标系。学习本节我们要掌握以下三方面的知识内容:
1.能够正确画出直角坐标系。
2.能在直角坐标系中,根据坐标找出点,由点求出坐标。坐标平面内的点和有序实数对是一一对应的。
3.掌握象限点、x轴及y轴上点的坐标的特征:
第一象限:(+,+)第二象限:(-,+)
第三象限:(-,-)第四象限:(+,-)
x轴上的点的纵坐标为0,表示为(x,0)
y轴上的点的横坐标为0,表示为(0,y)
本节小结
1、对于坐标平面内的任一点,都有唯一对有序实数与它对应.(
)
2、在直角坐标系内,原点的坐标是0.(
)
3、如图,点P的坐标是
4,3.(
)
4、如果点A(a
,-b)在第二象限,那么点B
(-a,b)在第四象限.(
)
5、若点P的坐标为(a,b),且a·b=0,则点P一定在坐标原点.
(
)
√
√
×
课堂练习
×
x
y
3
4
o
P
×
5、已知P点坐标为P(a-1,a-5)
①点P在x轴上,则a=
;
②点P在y轴上,则a=
;
③若a=-3
,则P在第
象限内;
④若a=3,则点P在第
象限内.
6、若点P(x,y)在第四象限,|x|=2,
|y|=3,则P点的坐标为
.
5
(2,-3)
1
三
四
课堂练习
拓展延伸:1、已知P点坐标为(2a+1,a-3)
①点P在x轴上,则a=
______
②点P在y轴上,则a=
;
③点P在第三象限内,则a的取值范围是
;
④点P在第四象限内,则a的取值范围是
_______________.
3
x
y
o
A
C
B
D
图①
2.如图①,写出边长为2的正方形ABCD的各顶点的坐标。
x
y
o
A
C
B
D
图②
如图②?
x
y
o
A
C
B
D
图③
如图③?
3、根据右图中的平面直角坐标系,
(1)写出□ABCD四个顶点的坐标
.
(2)试求出□ABCD的面积
.
(1)请在平面直角坐标系中描出点A(-3,-2).
(2)作出点A、点B关于x轴的对称点,并写出它们的坐标.
(3)作出点A、点B关于y轴的对称点,并写出它们的坐标.
(4)作出点A、点B关于原点的对称点,并写出它们的坐标.
点A(-3,-2)
关于X轴的对称点的坐标为___
,
关于y轴的对称点的坐标为__________,
关于原点的对称点的坐标为____________
(-3,2)
(3,-2)
(3,2)
P(a,b)关于x轴的对称点坐标为_______
P(a,b)关于y轴的对称点坐标为_____________
P(a,b)关于原点的对称点坐标为__________
(-
a,-
b)
(-
a,b)
(a,-
b)
横不变纵变
纵不变横变
横纵都要变
★
4.在平面直角坐标系内,已知点A(2,-2),在坐标轴上确定点P,使三角形AOP为等腰三角形,写出符合条件的P点坐标
5.已知点B(a,3),点C(-2,b)直线BC平行于y
轴,求a的值,并确定b的取值范围.
6、若点P(x,y)在
(1)第一象限,则x____0,y____0
(2)第二象限,则x____0,y____0
(3)第三象限,则x____0,y____0
(4)第四象限,则x____0,y____0
(5)x轴上,则x________,y_________
(6)y轴上,则x________,y_________
(7)原点上,则x________,y_________
(8)若xy>0,则点P在_______象限
(9)若xy<0
,则点P在_______象限
(10)若x2+y2=0,则点P在_______
Y
X
o
1
2
3
4
5
6
-1
1
6
5
4
3
2
-2
-3
-4
-5
-6
-7
-1
-2
-3
-4
-5
-6
-7
A
B
C
1.若xy>0,且x+y<0,试确定A(x,y)在哪个象限?
2.已知点M(a,-b)在第二象限,点N(a+b,-ab)在第几象限?
5.2平面直角坐标系(1)
1、什么是数轴?
复 习
·
单位长度
0
1
2
3
4
-3
-2
-1
原点
2、数轴上的点与
?一一对应
实数
这个点在数轴上的坐标
3、写出数轴上A、B、C各点的坐标:
A
B
C
o
1
2
3
4
5
6
-1
-2
-3
-4
-5
-6
4、平面上确定位置的方法
(1)用有序数对法
(2)用方向和距离法
归纳:
平面上确定一个位置一般
需要2个实数。而且两个实数的
意义不同,先后顺序不能调换。
第1列
第2列
第3列
第4列
第5列
第6列
第1行
第2行
第3行
第4行
第5行
第6行
讲台
问题:怎样表示你的座位?
小明
小亮
(3,4)
(5,6)
德育路
德育路
锡宅路
锡宅路
双象大酒店
后宅中学大门在德育路东边50米,锡宅路北边100米。
后宅中学大门
1、小明是怎样描述后宅中学大门的位置?
2、小明省去“北边”和“东边”
这几个字可以吗?
3、如果小明仅仅说在“锡宅路北边、德育路东边”,你能找到后宅中学大门吗?
锡宅路
德育路
后宅中学大门
50
100
北
东
4、如果小明只说在“锡宅路北边100米”,或只说在“德育路东边50米”,你能找到后宅中学的大门吗?
若将锡宅路与德育路看两条互相垂直的数轴,十字路口为它们的公共原点,这样就形成了一个平面直角坐标系。
x
y
o
60
40
20
80
20
-20
-40
-80
-100
40
80
60
-40
-40
-20
-60
100
100
后宅中学大门
锡宅路
德育路
x
y
o
-1
2
3
4
5
6
7
8
9
-2
-3
-4
-5
-6
-7
-8
-9
1
1
2
3
4
5
-1
-2
-3
-4
-5
平面上有公共原点且互相垂直的2条数轴构成平面直角坐标系,简称直角坐标系
水平方向的数轴称为x轴或横轴
竖直方向的数轴称为y轴或纵轴。
x轴和y轴统称坐标轴
公共原点O称为坐标原点
解析几何的创始人
──笛卡尔
笛卡尔(1596—1650),法国数学家。
他所创建的直角坐标系标志着代数与几何的第一次完美结合,使形形色色的代数方程表现为不同的几何图形,许多相当难解的几何题转化为代数题后能轻而易举地找到答案。
3
1
4
2
5
-2
-4
-1
-3
o
1
2
3
4
5
-4
-3
-2
-1
x
横轴
y
纵轴
原点
平面直角坐标系具有以下特征:
①两条数轴互相垂直
②原点重合
③通常取向右、向上为正方向
④单位长度一般取相同的
平面直角坐标系
3
1
4
2
5
-2
-4
-1
-3
0
1
2
3
4
5
-4
-3
-2
-1
x
(横轴)
y
(纵轴)
原点
第一象限
第二象限
第三象限
第四象限
两条坐标轴把平面分成四个区域,称为象限
注意:坐标轴是象限与象限之间的分界,因此坐标轴上的点不属于任何象限
-1
0
1
1
-1
Q
即:(m,n)
x
y
过Q点作x轴的垂线,过Q点作y轴的垂线,
已知点Q的位置,如何确定Q的坐标呢?
两垂足对应的数就是点Q的坐标。
m
n
横坐标在前,
纵坐标在后,
中间隔开用逗号
勿忘加括号!
它们的位置
a
过y轴上表示坐标为b的点画y轴的垂线
-1
0
1
1
-1
b
P
x
y
过x轴上表示坐标为a的点画x轴的垂线
这两条垂线的交点即为点P,
(a,b)
已知P的坐标为(a,b),如何确定P的位置呢?
y
o
-1
2
3
4
5
6
7
8
9
-2
-3
-4
-5
-6
-7
-8
-9
1
1
2
3
4
5
-1
-2
-3
-4
-5
A
(3,2)
B
(2,3)
C
D
E
分别在平面内确定点A(3,2)、B(2,3)的位置,并确定点C、D、E的坐标。
x
(-3,3)
(5,-3)
(-7,-5)
坐标平面上的点
一对有序实数
(+,+)
(-,+)
(-,-)
(+,-)
x
y
o
-1
2
3
4
5
6
7
8
9
-2
-3
-4
-5
-6
-7
-8
-9
1
1
2
3
4
5
-1
-2
-3
-4
-5
A
B
C
各象限内的点的坐标有何特征?
D
E
(-2,3)
(5,3)
(3,2)
(5,-4)
(-7,-5)
F
G
H
(-7,2)
(-5,-4)
(3,-5)
A
B
C
D
(3,0)
(-4,0)
(0,5)
(0,-4)
(0,0)
坐标轴上点有何特征?
在x轴上的点,
纵坐标等于0.
在y轴上的点,
横坐标等于0.
A(
3,
2
)
B(
0,-2
)
C(-3,-2)
D(-3,
0
)
E(-1.5,3.5)
F(
2,
-3
)
第一象限
第三象限
第二象限
第四象限
y轴上
x轴上
练一练:
下列各点分别在坐标平面的什么位置上?
本节课我们学面直角坐标系。学习本节我们要掌握以下三方面的知识内容:
1.能够正确画出直角坐标系。
2.能在直角坐标系中,根据坐标找出点,由点求出坐标。坐标平面内的点和有序实数对是一一对应的。
3.掌握象限点、x轴及y轴上点的坐标的特征:
第一象限:(+,+)第二象限:(-,+)
第三象限:(-,-)第四象限:(+,-)
x轴上的点的纵坐标为0,表示为(x,0)
y轴上的点的横坐标为0,表示为(0,y)
本节小结
1、对于坐标平面内的任一点,都有唯一对有序实数与它对应.(
)
2、在直角坐标系内,原点的坐标是0.(
)
3、如图,点P的坐标是
4,3.(
)
4、如果点A(a
,-b)在第二象限,那么点B
(-a,b)在第四象限.(
)
5、若点P的坐标为(a,b),且a·b=0,则点P一定在坐标原点.
(
)
√
√
×
课堂练习
×
x
y
3
4
o
P
×
5、已知P点坐标为P(a-1,a-5)
①点P在x轴上,则a=
;
②点P在y轴上,则a=
;
③若a=-3
,则P在第
象限内;
④若a=3,则点P在第
象限内.
6、若点P(x,y)在第四象限,|x|=2,
|y|=3,则P点的坐标为
.
5
(2,-3)
1
三
四
课堂练习
拓展延伸:1、已知P点坐标为(2a+1,a-3)
①点P在x轴上,则a=
______
②点P在y轴上,则a=
;
③点P在第三象限内,则a的取值范围是
;
④点P在第四象限内,则a的取值范围是
_______________.
3
x
y
o
A
C
B
D
图①
2.如图①,写出边长为2的正方形ABCD的各顶点的坐标。
x
y
o
A
C
B
D
图②
如图②?
x
y
o
A
C
B
D
图③
如图③?
3、根据右图中的平面直角坐标系,
(1)写出□ABCD四个顶点的坐标
.
(2)试求出□ABCD的面积
.
(1)请在平面直角坐标系中描出点A(-3,-2).
(2)作出点A、点B关于x轴的对称点,并写出它们的坐标.
(3)作出点A、点B关于y轴的对称点,并写出它们的坐标.
(4)作出点A、点B关于原点的对称点,并写出它们的坐标.
点A(-3,-2)
关于X轴的对称点的坐标为___
,
关于y轴的对称点的坐标为__________,
关于原点的对称点的坐标为____________
(-3,2)
(3,-2)
(3,2)
P(a,b)关于x轴的对称点坐标为_______
P(a,b)关于y轴的对称点坐标为_____________
P(a,b)关于原点的对称点坐标为__________
(-
a,-
b)
(-
a,b)
(a,-
b)
横不变纵变
纵不变横变
横纵都要变
★
4.在平面直角坐标系内,已知点A(2,-2),在坐标轴上确定点P,使三角形AOP为等腰三角形,写出符合条件的P点坐标
5.已知点B(a,3),点C(-2,b)直线BC平行于y
轴,求a的值,并确定b的取值范围.
6、若点P(x,y)在
(1)第一象限,则x____0,y____0
(2)第二象限,则x____0,y____0
(3)第三象限,则x____0,y____0
(4)第四象限,则x____0,y____0
(5)x轴上,则x________,y_________
(6)y轴上,则x________,y_________
(7)原点上,则x________,y_________
(8)若xy>0,则点P在_______象限
(9)若xy<0
,则点P在_______象限
(10)若x2+y2=0,则点P在_______
Y
X
o
1
2
3
4
5
6
-1
1
6
5
4
3
2
-2
-3
-4
-5
-6
-7
-1
-2
-3
-4
-5
-6
-7
A
B
C
1.若xy>0,且x+y<0,试确定A(x,y)在哪个象限?
2.已知点M(a,-b)在第二象限,点N(a+b,-ab)在第几象限?
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
