四川省仁寿县两校2020-2021学年高二下学期6月联考数学(文)试题 Word版含答案
文档属性
| 名称 | 四川省仁寿县两校2020-2021学年高二下学期6月联考数学(文)试题 Word版含答案 | 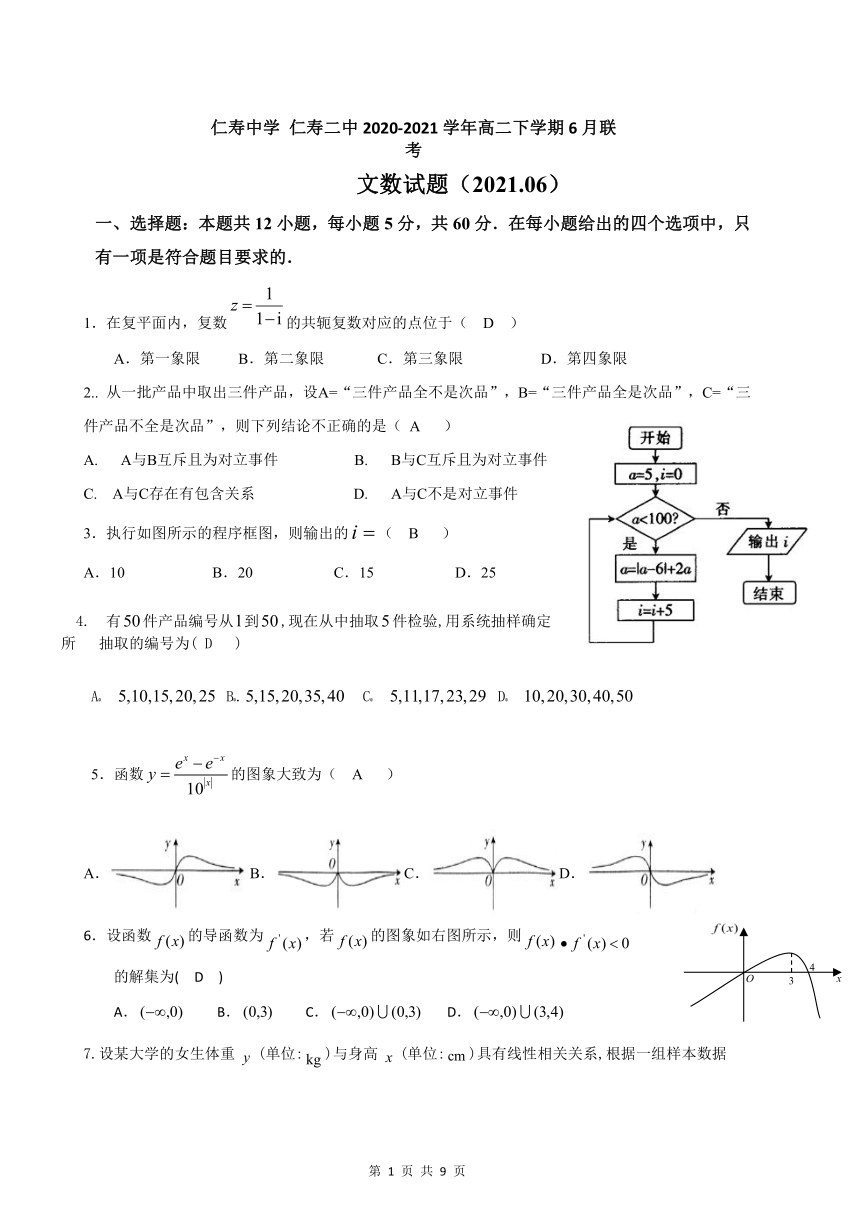 | |
| 格式 | doc | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-06 20:46:20 | ||
图片预览



文档简介
仁寿中学 仁寿二中2020-2021学年高二下学期6月联考
文数试题(2021.06)
选择题:本题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.在复平面内,复数的共轭复数对应的点位于( D )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
2.. 从一批产品中取出三件产品,设A=“三件产品全不是次品”,B=“三件产品全是次品”,C=“三件产品不全是次品”,则下列结论不正确的是( A )
A. A与B互斥且为对立事件 B. B与C互斥且为对立事件
C. A与C存在有包含关系 D. A与C不是对立事件
3.执行如图所示的程序框图,则输出的( B )
A.10 B.20 C.15 D.25
有件产品编号从到,现在从中抽取件检验,用系统抽样确定所 抽取的编号为( D )
A B. C D
5.函数的图象大致为( A )
A.B.C.D.
6.设函数的导函数为,若的图象如右图所示,则
的解集为( D )
A. B. C. D.
7.设某大学的女生体重(单位:)与身高(单位:)具有线性相关关系,根据一组样本数据,用最小二乘法建立的回归方程为,则下列结论中不正确的是(?D? )
A.与具有正的线性相关关系 B.回归直线过样本点的中心
C.若该大学某女生身高增加,则其体重约增加
D.若该大学某女生身高为,则可断定其体重必为
8. 已知地铁列车每10 min一班,在车站停1 min.则乘客到达站台立即乘上车的概率是( A )
A. B. C. D.
9.关于函数,的性质,以下说法正确的是( D )
A.函数的周期是 B.函数在上有极值
C.函数在单调递减 D.函数在内有最小值
10.我国古代数学名著《九章算术》中割圆术有:“割之弥细,所失弥少,割之又割,以至于不可割,则与圆周合体而无所失矣.”其体现的是一种无限与有限的转化过程,比如在中“…”即代表无限次重复,但原式却是个定值x,这可以通过方程确定出来,令,类似地,t等于( A )
A. B. C. D.
11.用反证法证明命题①:“已知,求证:”时,可假设“”;命题②:“若,则或”时,可假设“或”.以下结论正确的是( C )
A.①与②的假设都错误 B.①与②的假设都正确
C.①的假设正确,②的假设错误 D.①的假设错误,②的假设正确
12.函数,函数有5个零点,则实数的取值范围为( A )
A. B. C. D.
二、填空题:本题共4小题,每小题5分,共20分.
13、一个袋中装有2个红球和2个白球,现从袋中取出1球,然后放回袋中再取出一球,则取出的两个球同色的概率是 _______
14.数据的标准差是__ _______。
15.若,则 .
16.已知函数,若,则的最小值是 .
三、解答题:共70分.解答应写出文字说明、证明过程或演算步骤.
17.(本小题满分10分) 已知函数图象在点处切线斜率为,且时,有极值.(1)求的解析式;(2)求在上的最大值和最小值.
18.(本小题满分12分)2020年初的新冠疫情对零售业造成严重冲击,随着疫情逐步得到控制,各地经济逐渐得到恢复,以下是某地一超市2020年6月某星期的营业收入统计情况.
星期:x 1 2 3 4 5
营业收入:y(单位;万元) 5 7.5 9 10.5 13
(1)根据数据可知y与x之间存在较强线性关系,求出y关于x的线性回归方程;
(2)该超市为鼓励员工努力工作,制定如下奖励方案:若当天营业收入达到或超过8万元,则当天上班的每一位员工可获得一个50元的红包,若当天营业收人达到或超过12万元,则当天上班的每一位员工可获得一个100元的红包.假设某员工这5天中上了3天班,每天上班的可能性都一样,求该员工5天中获得红包奖励不少于100元的概率.
附:.
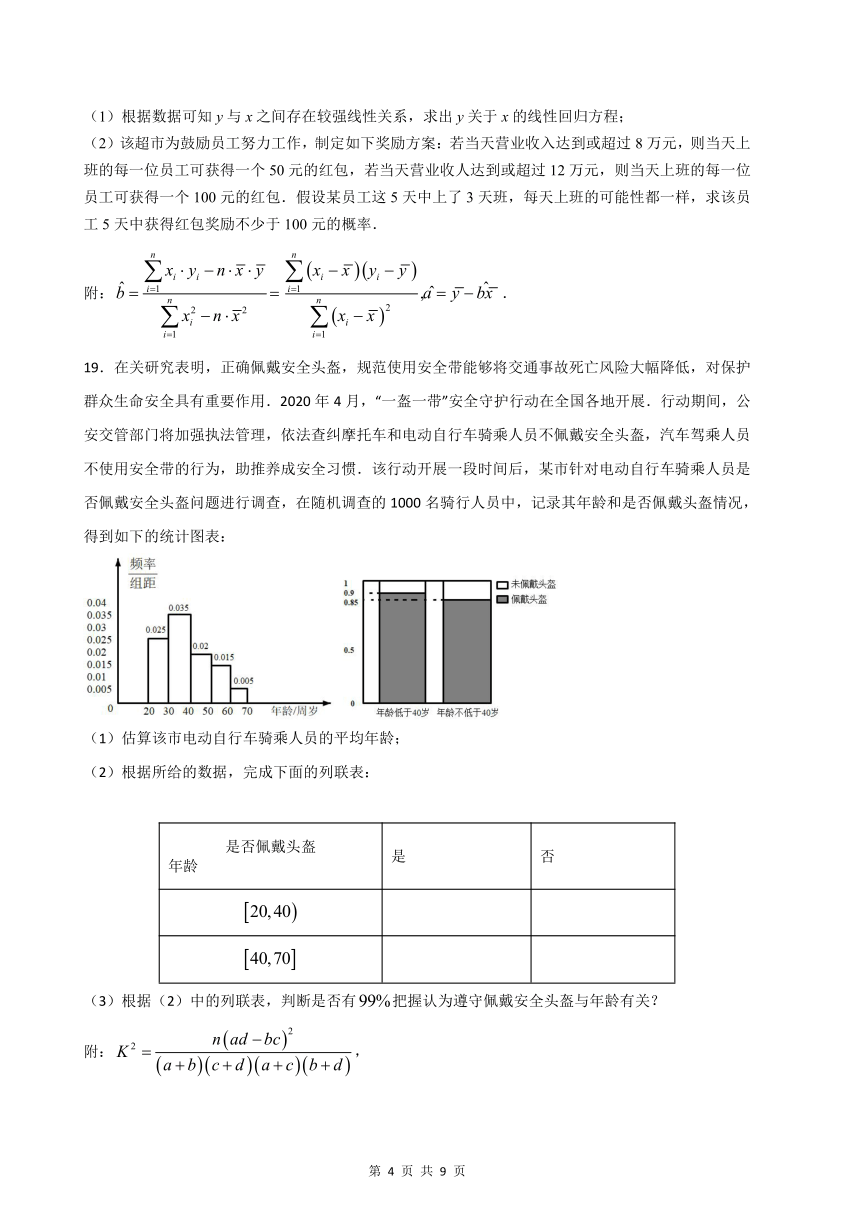
19.在关研究表明,正确佩戴安全头盔,规范使用安全带能够将交通事故死亡风险大幅降低,对保护群众生命安全具有重要作用.2020年4月,“一盔一带”安全守护行动在全国各地开展.行动期间,公安交管部门将加强执法管理,依法查纠摩托车和电动自行车骑乘人员不佩戴安全头盔,汽车驾乘人员不使用安全带的行为,助推养成安全习惯.该行动开展一段时间后,某市针对电动自行车骑乘人员是否佩戴安全头盔问题进行调查,在随机调查的1000名骑行人员中,记录其年龄和是否佩戴头盔情况,得到如下的统计图表:
(1)估算该市电动自行车骑乘人员的平均年龄;
(2)根据所给的数据,完成下面的列联表:
是否佩戴头盔 年龄 是 否
(3)根据(2)中的列联表,判断是否有把握认为遵守佩戴安全头盔与年龄有关?
附:,
0.050 0.010 0.001
3.841 6.635 10.828
2.20.某偏远贫困村积极响应国家“扶贫攻坚”政策,在对口帮扶单位的支持下建了一个工厂,已知每件产品的成本为元,预计当每件产品的售价为元时,年销量为万件.若每件产品的售价定为元时,预计年利润为万元
(1)试求每件产品的成本的值;
(2)当每件产品的售价定为多少元时?年利润(万元)最大,并求最大值.
21.(本小题满分12分)已知函数和
(1)若在上是增函数,求的取值范围.
(2)设函数的导数是,且,求在上的最小值
22.(本小题满分12分)已知函数.
(1)当时,求函数的单调区间;
(2)当时,求证:总存在唯一的极小值点,且.
第 4 页 共 4 页
文数试题(2021.06)
选择题:本题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.在复平面内,复数的共轭复数对应的点位于( D )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
2.. 从一批产品中取出三件产品,设A=“三件产品全不是次品”,B=“三件产品全是次品”,C=“三件产品不全是次品”,则下列结论不正确的是( A )
A. A与B互斥且为对立事件 B. B与C互斥且为对立事件
C. A与C存在有包含关系 D. A与C不是对立事件
3.执行如图所示的程序框图,则输出的( B )
A.10 B.20 C.15 D.25
有件产品编号从到,现在从中抽取件检验,用系统抽样确定所 抽取的编号为( D )
A B. C D
5.函数的图象大致为( A )
A.B.C.D.
6.设函数的导函数为,若的图象如右图所示,则
的解集为( D )
A. B. C. D.
7.设某大学的女生体重(单位:)与身高(单位:)具有线性相关关系,根据一组样本数据,用最小二乘法建立的回归方程为,则下列结论中不正确的是(?D? )
A.与具有正的线性相关关系 B.回归直线过样本点的中心
C.若该大学某女生身高增加,则其体重约增加
D.若该大学某女生身高为,则可断定其体重必为
8. 已知地铁列车每10 min一班,在车站停1 min.则乘客到达站台立即乘上车的概率是( A )
A. B. C. D.
9.关于函数,的性质,以下说法正确的是( D )
A.函数的周期是 B.函数在上有极值
C.函数在单调递减 D.函数在内有最小值
10.我国古代数学名著《九章算术》中割圆术有:“割之弥细,所失弥少,割之又割,以至于不可割,则与圆周合体而无所失矣.”其体现的是一种无限与有限的转化过程,比如在中“…”即代表无限次重复,但原式却是个定值x,这可以通过方程确定出来,令,类似地,t等于( A )
A. B. C. D.
11.用反证法证明命题①:“已知,求证:”时,可假设“”;命题②:“若,则或”时,可假设“或”.以下结论正确的是( C )
A.①与②的假设都错误 B.①与②的假设都正确
C.①的假设正确,②的假设错误 D.①的假设错误,②的假设正确
12.函数,函数有5个零点,则实数的取值范围为( A )
A. B. C. D.
二、填空题:本题共4小题,每小题5分,共20分.
13、一个袋中装有2个红球和2个白球,现从袋中取出1球,然后放回袋中再取出一球,则取出的两个球同色的概率是 _______
14.数据的标准差是__ _______。
15.若,则 .
16.已知函数,若,则的最小值是 .
三、解答题:共70分.解答应写出文字说明、证明过程或演算步骤.
17.(本小题满分10分) 已知函数图象在点处切线斜率为,且时,有极值.(1)求的解析式;(2)求在上的最大值和最小值.
18.(本小题满分12分)2020年初的新冠疫情对零售业造成严重冲击,随着疫情逐步得到控制,各地经济逐渐得到恢复,以下是某地一超市2020年6月某星期的营业收入统计情况.
星期:x 1 2 3 4 5
营业收入:y(单位;万元) 5 7.5 9 10.5 13
(1)根据数据可知y与x之间存在较强线性关系,求出y关于x的线性回归方程;
(2)该超市为鼓励员工努力工作,制定如下奖励方案:若当天营业收入达到或超过8万元,则当天上班的每一位员工可获得一个50元的红包,若当天营业收人达到或超过12万元,则当天上班的每一位员工可获得一个100元的红包.假设某员工这5天中上了3天班,每天上班的可能性都一样,求该员工5天中获得红包奖励不少于100元的概率.
附:.
19.在关研究表明,正确佩戴安全头盔,规范使用安全带能够将交通事故死亡风险大幅降低,对保护群众生命安全具有重要作用.2020年4月,“一盔一带”安全守护行动在全国各地开展.行动期间,公安交管部门将加强执法管理,依法查纠摩托车和电动自行车骑乘人员不佩戴安全头盔,汽车驾乘人员不使用安全带的行为,助推养成安全习惯.该行动开展一段时间后,某市针对电动自行车骑乘人员是否佩戴安全头盔问题进行调查,在随机调查的1000名骑行人员中,记录其年龄和是否佩戴头盔情况,得到如下的统计图表:
(1)估算该市电动自行车骑乘人员的平均年龄;
(2)根据所给的数据,完成下面的列联表:
是否佩戴头盔 年龄 是 否
(3)根据(2)中的列联表,判断是否有把握认为遵守佩戴安全头盔与年龄有关?
附:,
0.050 0.010 0.001
3.841 6.635 10.828
2.20.某偏远贫困村积极响应国家“扶贫攻坚”政策,在对口帮扶单位的支持下建了一个工厂,已知每件产品的成本为元,预计当每件产品的售价为元时,年销量为万件.若每件产品的售价定为元时,预计年利润为万元
(1)试求每件产品的成本的值;
(2)当每件产品的售价定为多少元时?年利润(万元)最大,并求最大值.
21.(本小题满分12分)已知函数和
(1)若在上是增函数,求的取值范围.
(2)设函数的导数是,且,求在上的最小值
22.(本小题满分12分)已知函数.
(1)当时,求函数的单调区间;
(2)当时,求证:总存在唯一的极小值点,且.
第 4 页 共 4 页
同课章节目录
