青岛版六三制四年级上册六 快捷的物流运输——解决问题路程、速度与时间的关系.pptx课件(29张PPT)
文档属性
| 名称 | 青岛版六三制四年级上册六 快捷的物流运输——解决问题路程、速度与时间的关系.pptx课件(29张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 4.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-07 10:41:19 | ||
图片预览





文档简介
青岛版数学
四年级上册
路程、速度与时间的关系
六 快捷的物流运输
——解决问题
青岛版数学四年级(上)
结合具体情境,理解和掌握速度、时间和路程的含义,并学会用统一的单位符号来表示速度。
从实际生活中抽象出时间、速度和路程之间的关系,并能用这种关系解决问题。
初步构建相遇问题的数学模型。
感受数学与生活的密切联系,增进热爱生活的情感,提高解决简单实际问题的能力。
【重点】
理解速度、时间和路程之间的关系。
【难点】
理解速度的概念,可以解决相遇问题。
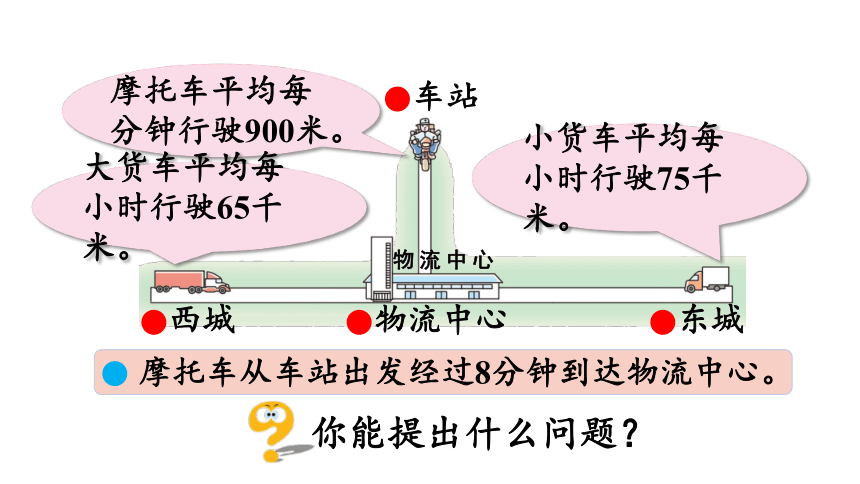
摩托车平均每分钟行驶900米。
大货车平均每小时行驶65千米。
小货车平均每小时行驶75千米。
你能提出什么问题?
车站
西城
物流中心
东城
物流中心
摩托车从车站出发经过8分钟到达物流中心。
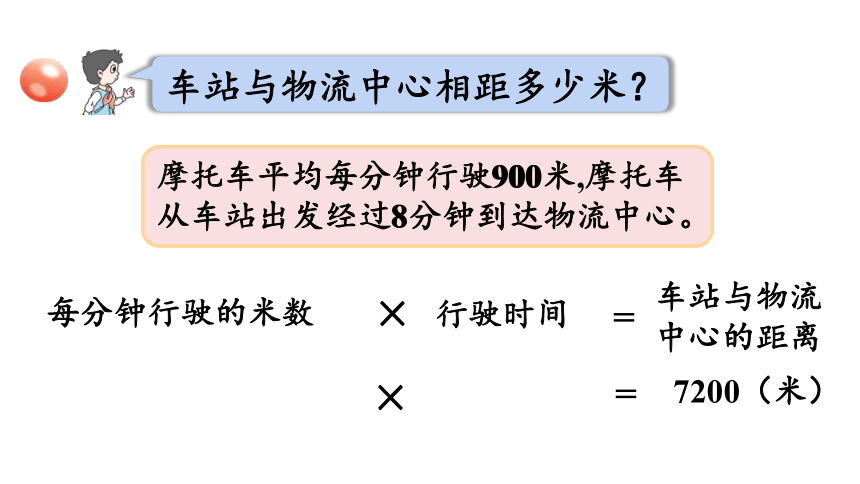
摩托车平均每分钟行驶900米,摩托车从车站出发经过8分钟到达物流中心。
900
每分钟行驶的米数
×
行驶时间
=
车站与物流中心的距离
×
=
7200(米)
车站与物流中心相距多少米?
8
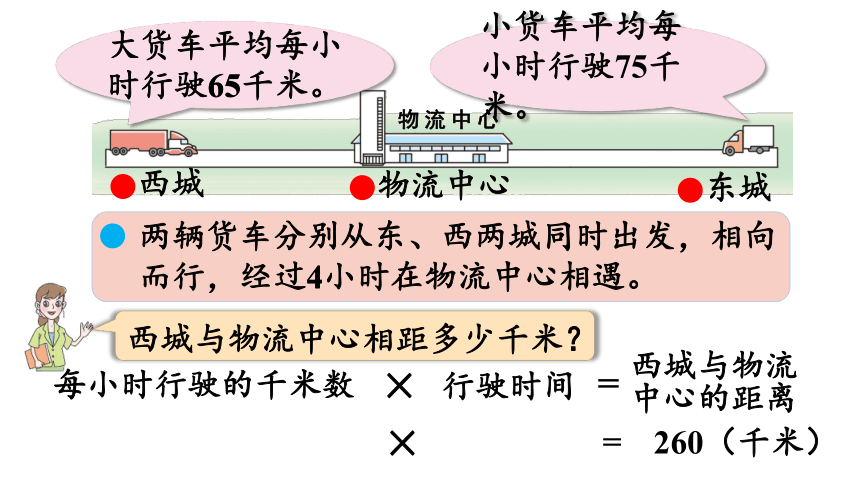
大货车平均每小时行驶65千米。
小货车平均每小时行驶75千米。
西城
物流中心
东城
物流中心
两辆货车分别从东、西两城同时出发,相向
而行,经过4小时在物流中心相遇。
每小时行驶的千米数
×
行驶时间
=
西城与物流中心的距离
×
=
260(千米)
西城与物流中心相距多少千米?
65
4
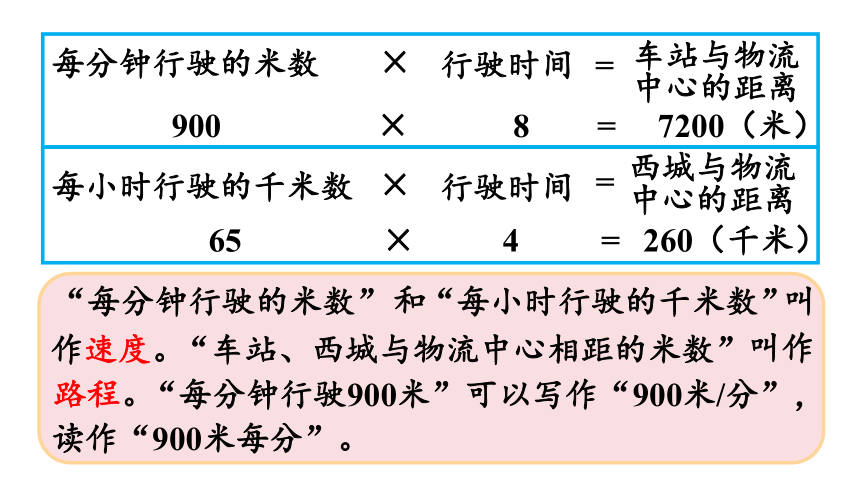
900
每分钟行驶的米数
×
行驶时间
=
车站与物流中心的距离
×
=
7200(米)
8
每小时行驶的千米数
×
行驶时间
=
西城与物流中心的距离
×
=
260(千米)
65
4
“每分钟行驶的米数”
和
“每小时行驶的千米数”
叫
作速度。
“车站、西城与物流中心相距的米数”
叫作
路程。
“每分钟行驶900米”可以写作“900米/分”,
读作“900米每分”。
摩托车平均每分钟行驶900米,8分钟能行驶7200米。
900米/分 × 8分 = 7200米
速度 × 时间 = 路程
你能说说速度、时间、路程之间的关系吗?
摩托车8分钟行驶7200米,平均每分钟行驶900米。
7200米 ÷ 8分 = 900米/分
路程 ÷ 时间 = 速度
你能说说速度、时间、路程之间的关系吗?
从车站到物流中心的距离是7200米,摩托车平均每分钟行驶900米,需要8分钟到达。
7200米 ÷ 900米/分 = 8分
路程 ÷ 速度 = 时间
你能说说速度、时间、路程之间的关系吗?
速度、时间和路程的关系
路程 ÷ 速度 = 时间
速度 × 时间 = 路程
路程 ÷ 时间 = 速度
知道其中的任意两个量,可以根据三者的关系求出第三个量。
东、西两城相距多少千米?
大货车平均每小时行驶65千米。
小货车平均每小时行驶75千米。
西城
物流中心
东城
两辆货车分别从东、西两城同时出发,相向
而行,经过4小时在物流中心相遇。
物流中心
求东、西两城相距多少千米,就是求两辆车行驶的总路程。
我们演示一下。
求东、西两城相距多少千米,就是求两辆车行驶的总路程。
还可以画线段图整理条件和问题。
65千米
西城
东城
75千米
物流中心
?千米
65千米
西城
东城
75千米
物流中心
?千米
65 × 4
75 ×4
+
先求每辆车4小时行驶的路程,再求两辆车行驶的总路程,也就是东、西两城相距的距离。
65×4+75×4
= 260 + 300
= 560(千米)
答:东、西两城相距 560 千米。
65千米
西城
东城
75千米
物流中心
?千米
65+75
65+75
65+75
65+75
(65 + 75)× 4
= 140 × 4
= 560(千米)
答:东、西两城相距 560 千米。
先求两辆车1小时共行驶的路程,再求两辆车4小时共行驶的路程,也就是东、西两城相距的距离。
(教材第82页“自主练习”)
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}交通工具
自行车
摩托车
轿 车
路程(千米)
30
150
时间(时)
2
7
速度(千米/时)
50
85
15
路程÷时间=速度
路程÷速度=时间
3
速度×时间=路程
595
先说说速度、时间和路程的关系,再填写下表。
1
(教材第82页“自主练习”)
甲、乙两列火车分别从东、西两地同时相对开出,5小时后相遇。甲车的速度是110千米/时,乙车的速度是100千米/时。求东、西两地间的路程。(先画图整理条件和问题,再解答。)
2
(110+100)×5
答:东、西两地间的路程是1050千米。
乙
甲
100千米
?千米
110千米
=210×5
=1050(千米)
110×5+100×5
=550+500
=1050(千米)
甲、乙两辆客车同时从同一车站相背开出,甲车每小时行驶89千米,乙车每小时行驶97千米。3小时后两车相距多少千米?
3
(89+97)×3
=186×3
=558(千米)
答:3小时后两车相距558千米。
两个工程队共同开凿一条隧道,分别从两端相向施工。甲队每天开凿24米,乙队每天开凿21米,21天完工。这条隧道长多少米?
4
(24+21)×21
=45×21
=945(米)
答:这条隧道长945米。
两辆汽车同时从甲、乙两地同时出发相向而行,一辆每小时行65千米,另一辆每小时行70千米。3小时后两车仍相距55千米,甲、乙两地相距多少千米?
5
(65+70)×3+55
=405+55
=460(千米)
答:甲、乙两地相距460千米。
从甲地到乙地的铁路长558千米。两列火车从两地同时相对开出,甲地开出的火车,平均每小时行44千米;乙地开出的火车,平均每小时行49千米。两车开出后几小时相遇?
6
答:两车开出后6小时相遇。
=558÷93
=6(小时)
558÷(44+49)
总路程÷速度和=相遇时间
我知道速度和路程的概念。
同学们,这节课你们学会了哪些知识?
单位时间行驶的距离叫作速度。从行驶的起点到终点的距离叫作路程。
我知道了速度、时间和路程之间的关系。
速度×时间=路程
路程÷时间=速度
路程÷速度=时间
同学们,这节课你们学会了哪些知识?
我知道了相遇问题包含两个速度和一个相遇时间。解决这类问题时, 可以用画线段图的方法分析题意。
速度和、相遇时间、总路程之间的关系:速度和×相遇时间=总路程
同学们,这节课你们学会了哪些知识?
相关练习。
02
01
自主练习第2、4、5、6题。
四年级上册
路程、速度与时间的关系
六 快捷的物流运输
——解决问题
青岛版数学四年级(上)
结合具体情境,理解和掌握速度、时间和路程的含义,并学会用统一的单位符号来表示速度。
从实际生活中抽象出时间、速度和路程之间的关系,并能用这种关系解决问题。
初步构建相遇问题的数学模型。
感受数学与生活的密切联系,增进热爱生活的情感,提高解决简单实际问题的能力。
【重点】
理解速度、时间和路程之间的关系。
【难点】
理解速度的概念,可以解决相遇问题。
摩托车平均每分钟行驶900米。
大货车平均每小时行驶65千米。
小货车平均每小时行驶75千米。
你能提出什么问题?
车站
西城
物流中心
东城
物流中心
摩托车从车站出发经过8分钟到达物流中心。
摩托车平均每分钟行驶900米,摩托车从车站出发经过8分钟到达物流中心。
900
每分钟行驶的米数
×
行驶时间
=
车站与物流中心的距离
×
=
7200(米)
车站与物流中心相距多少米?
8
大货车平均每小时行驶65千米。
小货车平均每小时行驶75千米。
西城
物流中心
东城
物流中心
两辆货车分别从东、西两城同时出发,相向
而行,经过4小时在物流中心相遇。
每小时行驶的千米数
×
行驶时间
=
西城与物流中心的距离
×
=
260(千米)
西城与物流中心相距多少千米?
65
4
900
每分钟行驶的米数
×
行驶时间
=
车站与物流中心的距离
×
=
7200(米)
8
每小时行驶的千米数
×
行驶时间
=
西城与物流中心的距离
×
=
260(千米)
65
4
“每分钟行驶的米数”
和
“每小时行驶的千米数”
叫
作速度。
“车站、西城与物流中心相距的米数”
叫作
路程。
“每分钟行驶900米”可以写作“900米/分”,
读作“900米每分”。
摩托车平均每分钟行驶900米,8分钟能行驶7200米。
900米/分 × 8分 = 7200米
速度 × 时间 = 路程
你能说说速度、时间、路程之间的关系吗?
摩托车8分钟行驶7200米,平均每分钟行驶900米。
7200米 ÷ 8分 = 900米/分
路程 ÷ 时间 = 速度
你能说说速度、时间、路程之间的关系吗?
从车站到物流中心的距离是7200米,摩托车平均每分钟行驶900米,需要8分钟到达。
7200米 ÷ 900米/分 = 8分
路程 ÷ 速度 = 时间
你能说说速度、时间、路程之间的关系吗?
速度、时间和路程的关系
路程 ÷ 速度 = 时间
速度 × 时间 = 路程
路程 ÷ 时间 = 速度
知道其中的任意两个量,可以根据三者的关系求出第三个量。
东、西两城相距多少千米?
大货车平均每小时行驶65千米。
小货车平均每小时行驶75千米。
西城
物流中心
东城
两辆货车分别从东、西两城同时出发,相向
而行,经过4小时在物流中心相遇。
物流中心
求东、西两城相距多少千米,就是求两辆车行驶的总路程。
我们演示一下。
求东、西两城相距多少千米,就是求两辆车行驶的总路程。
还可以画线段图整理条件和问题。
65千米
西城
东城
75千米
物流中心
?千米
65千米
西城
东城
75千米
物流中心
?千米
65 × 4
75 ×4
+
先求每辆车4小时行驶的路程,再求两辆车行驶的总路程,也就是东、西两城相距的距离。
65×4+75×4
= 260 + 300
= 560(千米)
答:东、西两城相距 560 千米。
65千米
西城
东城
75千米
物流中心
?千米
65+75
65+75
65+75
65+75
(65 + 75)× 4
= 140 × 4
= 560(千米)
答:东、西两城相距 560 千米。
先求两辆车1小时共行驶的路程,再求两辆车4小时共行驶的路程,也就是东、西两城相距的距离。
(教材第82页“自主练习”)
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}交通工具
自行车
摩托车
轿 车
路程(千米)
30
150
时间(时)
2
7
速度(千米/时)
50
85
15
路程÷时间=速度
路程÷速度=时间
3
速度×时间=路程
595
先说说速度、时间和路程的关系,再填写下表。
1
(教材第82页“自主练习”)
甲、乙两列火车分别从东、西两地同时相对开出,5小时后相遇。甲车的速度是110千米/时,乙车的速度是100千米/时。求东、西两地间的路程。(先画图整理条件和问题,再解答。)
2
(110+100)×5
答:东、西两地间的路程是1050千米。
乙
甲
100千米
?千米
110千米
=210×5
=1050(千米)
110×5+100×5
=550+500
=1050(千米)
甲、乙两辆客车同时从同一车站相背开出,甲车每小时行驶89千米,乙车每小时行驶97千米。3小时后两车相距多少千米?
3
(89+97)×3
=186×3
=558(千米)
答:3小时后两车相距558千米。
两个工程队共同开凿一条隧道,分别从两端相向施工。甲队每天开凿24米,乙队每天开凿21米,21天完工。这条隧道长多少米?
4
(24+21)×21
=45×21
=945(米)
答:这条隧道长945米。
两辆汽车同时从甲、乙两地同时出发相向而行,一辆每小时行65千米,另一辆每小时行70千米。3小时后两车仍相距55千米,甲、乙两地相距多少千米?
5
(65+70)×3+55
=405+55
=460(千米)
答:甲、乙两地相距460千米。
从甲地到乙地的铁路长558千米。两列火车从两地同时相对开出,甲地开出的火车,平均每小时行44千米;乙地开出的火车,平均每小时行49千米。两车开出后几小时相遇?
6
答:两车开出后6小时相遇。
=558÷93
=6(小时)
558÷(44+49)
总路程÷速度和=相遇时间
我知道速度和路程的概念。
同学们,这节课你们学会了哪些知识?
单位时间行驶的距离叫作速度。从行驶的起点到终点的距离叫作路程。
我知道了速度、时间和路程之间的关系。
速度×时间=路程
路程÷时间=速度
路程÷速度=时间
同学们,这节课你们学会了哪些知识?
我知道了相遇问题包含两个速度和一个相遇时间。解决这类问题时, 可以用画线段图的方法分析题意。
速度和、相遇时间、总路程之间的关系:速度和×相遇时间=总路程
同学们,这节课你们学会了哪些知识?
相关练习。
02
01
自主练习第2、4、5、6题。
