苏科版数学八年级下册 9.3平行四边形教案
文档属性
| 名称 | 苏科版数学八年级下册 9.3平行四边形教案 |
|
|
| 格式 | doc | ||
| 文件大小 | 160.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-07 07:40:54 | ||
图片预览


文档简介
9.3 平行四边形
教学目标:
1.经历探索平行四边形条件的过程,会利用定理判定四边形是平行四边形;
2.在探索平行四边形条件的过程中能够进行有条理的思考并进行简单的推理;
3.经历操作、探索、合作、交流等活动,营造和谐、平等的学习氛围.
教学重难点:平行四边形条件的过程的探索及应用.平行四边形条件的探索
教学过程:
1、问题情境
(1)回忆平行四边形的概念;
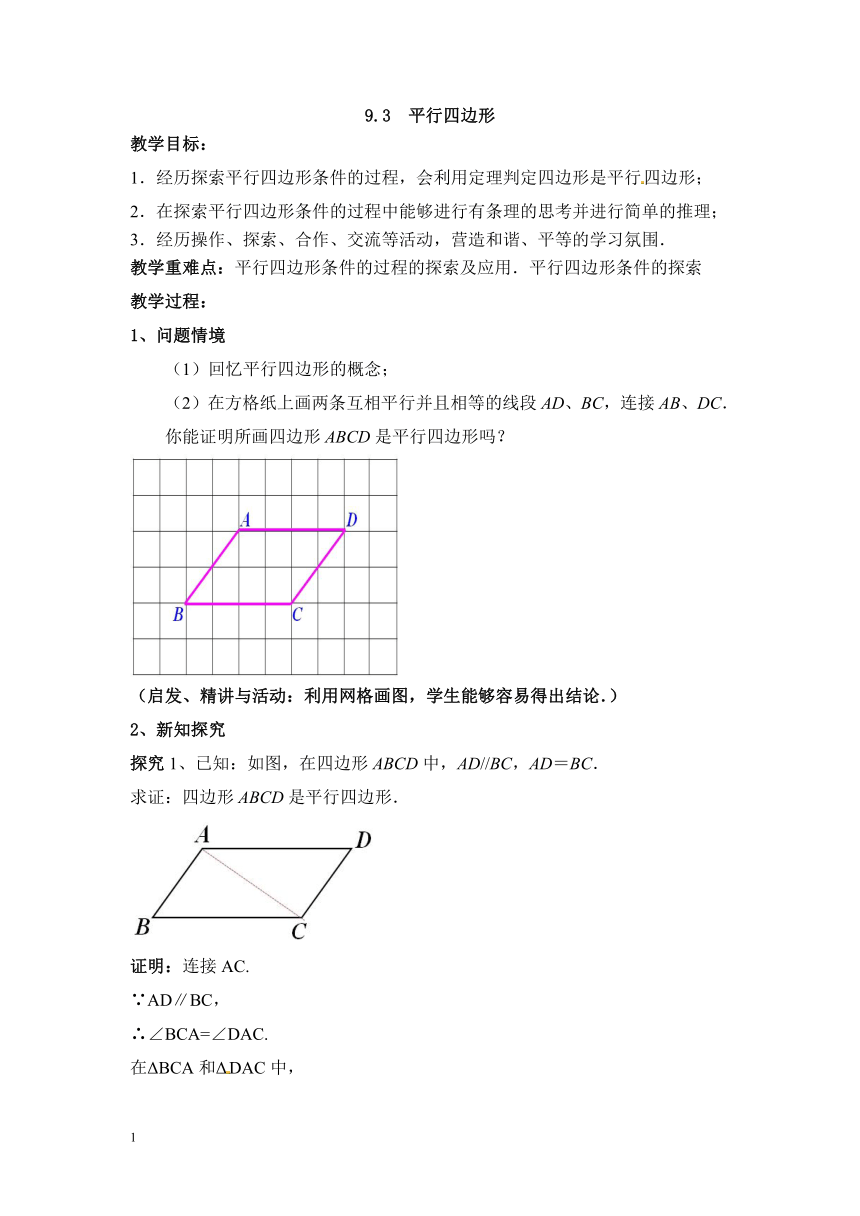
(2)在方格纸上画两条互相平行并且相等的线段AD、BC,连接AB、DC.
你能证明所画四边形ABCD是平行四边形吗?
(启发、精讲与活动:利用网格画图,学生能够容易得出结论.)
2、新知探究
探究1、已知:如图,在四边形ABCD中,AD//BC,AD=BC.
求证:四边形ABCD是平行四边形.
证明:连接AC.
∵AD∥BC,
∴∠BCA=∠DAC.
在ΔBCA和ΔDAC中,
CB=AD,
∠BCA=∠DAC,
CA=AC,
∴ ΔBCA≌ΔDAC
∴ ∠BAC= ∠DCA.
∴ AB∥CD.
∴四边形ABCD是平行四边形(两组对边分别平行的四边形是平行四边形).
(启发、精讲与活动:通过学生操作、思考,利用平行四边形的概念,进一步证明了一组对边平行且相等的四边形是平行四边形,从而加深学生的理解.)
定理:
一组对边平行且相等的四边形是平行四边形.
几何语言:
∵AD//BC,AD=BC,
∴四边形ABCD是平行四边形.
探究2、在四边形ABCD中,AB=CD,AD=BC.四边形ABCD是平行四边形吗?证明你的结论.
证明:连结AC
在△ABC和△CDA中
AB=CD(已知)
AD=CB (已知)
AC=CA (公共边)
∴△ABC≌△CDA(SSS)
∴∠1=∠2,∠3=∠4(全等三角形的对应角相等)
∴ AB∥CD,AD∥BC (内错角相等,两直线平行)
∴四边形ABCD是平行四边形(两组对边分别平行的四边形是平行四边形)
(启发、精讲与活动:使学生能够运用平行四边形的概念和定理证明四边形是平行四边形,从而得到两组对边分别相等的四边形是平行四边形.)
定理:
两组对边分别相等的四边形是平行四边形.
几何语言:
∵AB=CD,AD=BC,
∴四边形ABCD是平行四边形.
3、新知应用
已知:如图,在□ABCD中,点E、F分别在AD、BC上,且AE=CF.
求证:四边形BFDE是平行四边形.
证明:∵四边形ABCD是平行四边形,∴AD=BC,AD∥BC(平行四边形的对边平行且相等).
∵AE=CF,
∴AD-AE=BC-CF,
即 DE=BF.
∴四边形BFDE是平行四边形(一组对边平行且相等的四边形是平行四边形)
(启发、精讲与活动:培养学生运用几何语言进行说理的规范性.)
4、拓展延伸
如图,在□ABCD中,AE⊥BD,CF⊥BD,垂足分别是E、F,求证:四边形AECF是平行四边形.
(启发、精讲与活动:通过练习设置,使学生在运用新知识的过程中能够进行有条理的思考并进行简单的推理.)
5、课堂小结
探索平行四边形条件有几种方法?
(目的:培养学生反思自己学习过程的意识,充分发挥学生的主体作用,从而培养归纳、整理、表达的能力.)
8、板书设计
9.3 平行四边形(2)
(一)图形语言; (二)文字语言; (三)符合语言; (四)知识运用
1、两组对边分别平行的四边形是平行四边形 ∵AD//BC,AB//DC, 1、
∴四边形ABCD是平行四边形.
2、一组对边平行且相等的四边形是平行四边形. ∵AD//BC,AD=BC, 2、
∴四边形ABCD是平行四边形.
3、两组对边分别相等的四边形是平行四边形. ∵AB=CD,AD=BC, 3、
∴四边形ABCD是平行四边形.
9、课后作业
习题9.3(2).与《评价手册》9.3(2)
(目的是巩固本节课所学知识.)
教学反思:
利用平行四边形的条件解题比较容易,但综合平行四边形的性质解题有一部分学生不太熟练。
2
教学目标:
1.经历探索平行四边形条件的过程,会利用定理判定四边形是平行四边形;
2.在探索平行四边形条件的过程中能够进行有条理的思考并进行简单的推理;
3.经历操作、探索、合作、交流等活动,营造和谐、平等的学习氛围.
教学重难点:平行四边形条件的过程的探索及应用.平行四边形条件的探索
教学过程:
1、问题情境
(1)回忆平行四边形的概念;
(2)在方格纸上画两条互相平行并且相等的线段AD、BC,连接AB、DC.
你能证明所画四边形ABCD是平行四边形吗?
(启发、精讲与活动:利用网格画图,学生能够容易得出结论.)
2、新知探究
探究1、已知:如图,在四边形ABCD中,AD//BC,AD=BC.
求证:四边形ABCD是平行四边形.
证明:连接AC.
∵AD∥BC,
∴∠BCA=∠DAC.
在ΔBCA和ΔDAC中,
CB=AD,
∠BCA=∠DAC,
CA=AC,
∴ ΔBCA≌ΔDAC
∴ ∠BAC= ∠DCA.
∴ AB∥CD.
∴四边形ABCD是平行四边形(两组对边分别平行的四边形是平行四边形).
(启发、精讲与活动:通过学生操作、思考,利用平行四边形的概念,进一步证明了一组对边平行且相等的四边形是平行四边形,从而加深学生的理解.)
定理:
一组对边平行且相等的四边形是平行四边形.
几何语言:
∵AD//BC,AD=BC,
∴四边形ABCD是平行四边形.
探究2、在四边形ABCD中,AB=CD,AD=BC.四边形ABCD是平行四边形吗?证明你的结论.
证明:连结AC
在△ABC和△CDA中
AB=CD(已知)
AD=CB (已知)
AC=CA (公共边)
∴△ABC≌△CDA(SSS)
∴∠1=∠2,∠3=∠4(全等三角形的对应角相等)
∴ AB∥CD,AD∥BC (内错角相等,两直线平行)
∴四边形ABCD是平行四边形(两组对边分别平行的四边形是平行四边形)
(启发、精讲与活动:使学生能够运用平行四边形的概念和定理证明四边形是平行四边形,从而得到两组对边分别相等的四边形是平行四边形.)
定理:
两组对边分别相等的四边形是平行四边形.
几何语言:
∵AB=CD,AD=BC,
∴四边形ABCD是平行四边形.
3、新知应用
已知:如图,在□ABCD中,点E、F分别在AD、BC上,且AE=CF.
求证:四边形BFDE是平行四边形.
证明:∵四边形ABCD是平行四边形,∴AD=BC,AD∥BC(平行四边形的对边平行且相等).
∵AE=CF,
∴AD-AE=BC-CF,
即 DE=BF.
∴四边形BFDE是平行四边形(一组对边平行且相等的四边形是平行四边形)
(启发、精讲与活动:培养学生运用几何语言进行说理的规范性.)
4、拓展延伸
如图,在□ABCD中,AE⊥BD,CF⊥BD,垂足分别是E、F,求证:四边形AECF是平行四边形.
(启发、精讲与活动:通过练习设置,使学生在运用新知识的过程中能够进行有条理的思考并进行简单的推理.)
5、课堂小结
探索平行四边形条件有几种方法?
(目的:培养学生反思自己学习过程的意识,充分发挥学生的主体作用,从而培养归纳、整理、表达的能力.)
8、板书设计
9.3 平行四边形(2)
(一)图形语言; (二)文字语言; (三)符合语言; (四)知识运用
1、两组对边分别平行的四边形是平行四边形 ∵AD//BC,AB//DC, 1、
∴四边形ABCD是平行四边形.
2、一组对边平行且相等的四边形是平行四边形. ∵AD//BC,AD=BC, 2、
∴四边形ABCD是平行四边形.
3、两组对边分别相等的四边形是平行四边形. ∵AB=CD,AD=BC, 3、
∴四边形ABCD是平行四边形.
9、课后作业
习题9.3(2).与《评价手册》9.3(2)
(目的是巩固本节课所学知识.)
教学反思:
利用平行四边形的条件解题比较容易,但综合平行四边形的性质解题有一部分学生不太熟练。
2
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
