2.1 有理数课件 2021-2022学年北师大版七年级上册数学(33张)
文档属性
| 名称 | 2.1 有理数课件 2021-2022学年北师大版七年级上册数学(33张) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-06 19:30:36 | ||
图片预览






文档简介
(共33张PPT)
北师大版·七年级上册
第二章
有理数及其运算
1
有理数
观
察
城市
天气
高温
低温
城市
天气
高温
低温
哈尔滨
小雨
15
6
长春
多云
18
10
沈阳
小雨
19
7
天津
小雨
12
8
呼和浩特
雨夹雪
8
﹣3
乌鲁木齐
晴
4
﹣3
西宁
小雪
5
﹣4
银川
小雪
0
﹣3
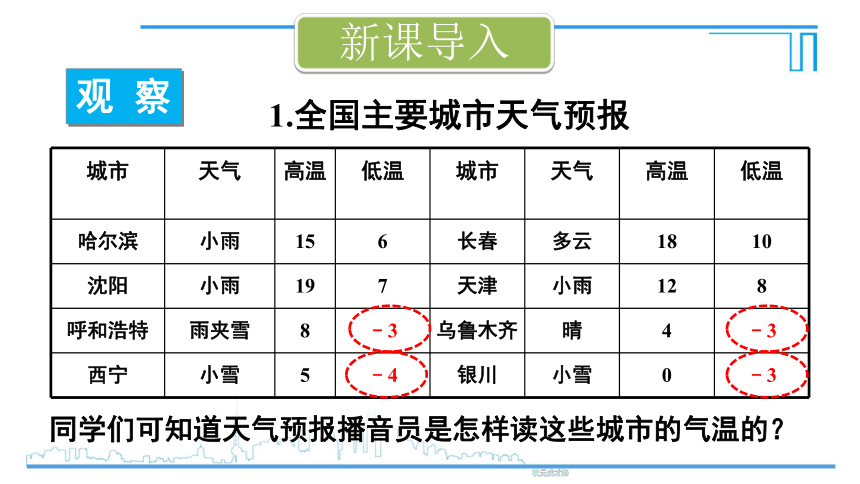
1.全国主要城市天气预报
同学们可知道天气预报播音员是怎样读这些城市的气温的?
新课导入
高度看作0
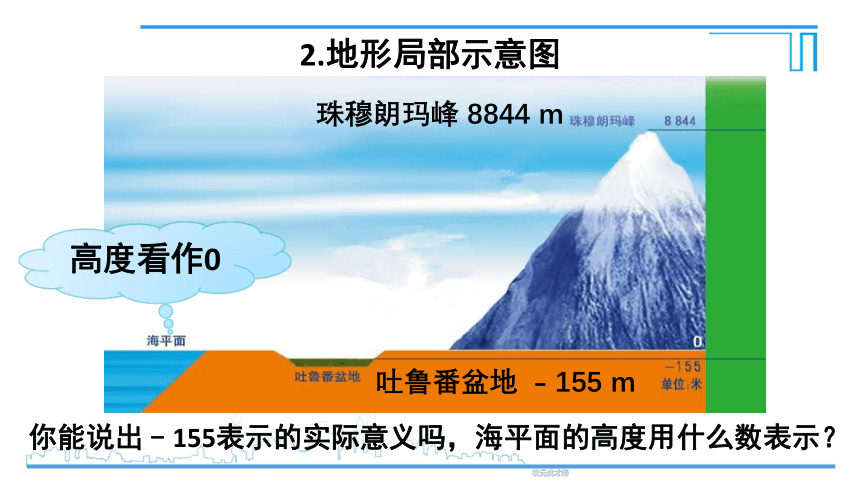
2.地形局部示意图
珠穆朗玛峰
8844
m
吐鲁番盆地
﹣155
m
你能说出﹣155表示的实际意义吗,海平面的高度用什么数表示?
探索新知
正数和负数的概念
知识点1
答对
不回答
答错
某班举行知识竞赛,评分标准是:答对一题加1分,答错一题扣1分,不回答得0分;每个队的基本分均为0分.两队答题情况如下表:
扣1分
加1分
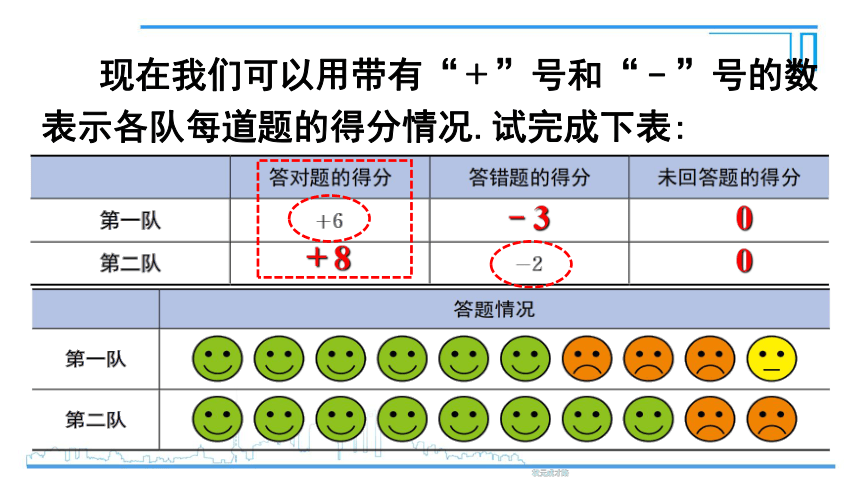
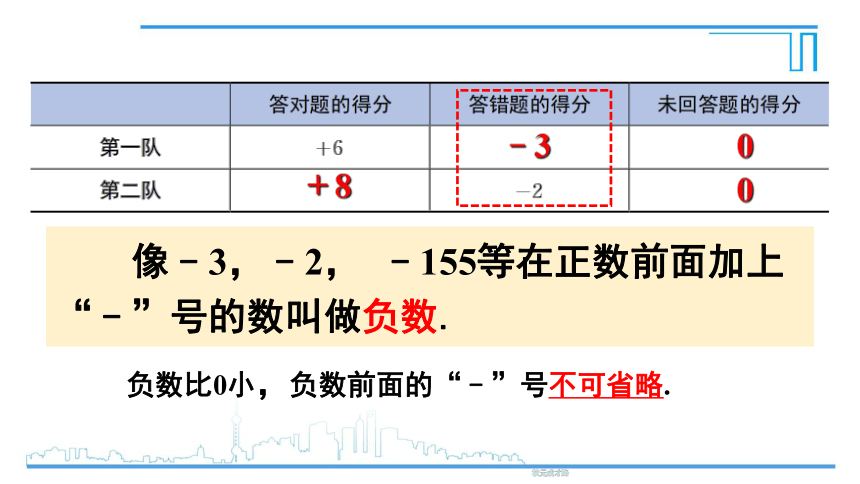
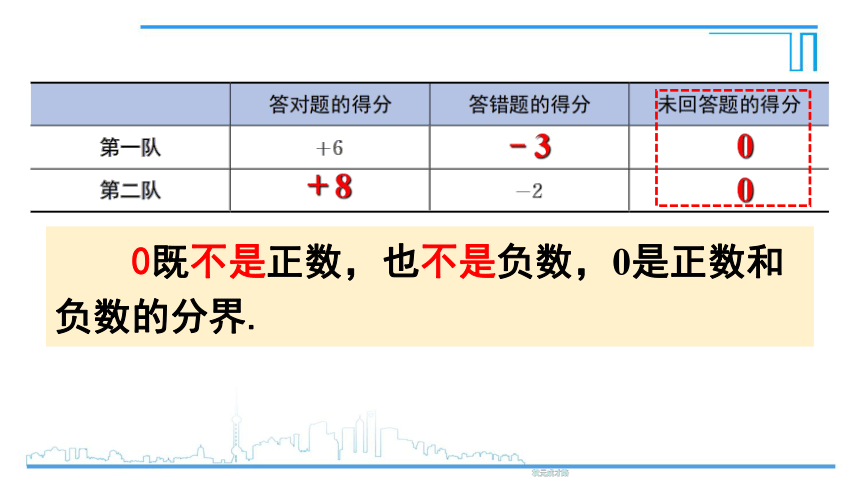
现在我们可以用带有“﹢”号和“﹣”号的数表示各队每道题的得分情况.试完成下表:
﹣3
0
﹢8
0
﹣3
0
﹢8
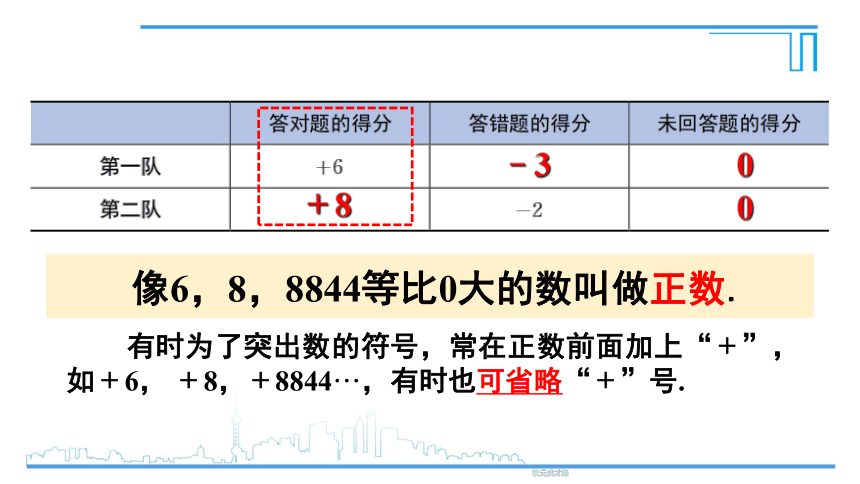
像6,8,8844等比0大的数叫做正数.
有时为了突出数的符号,常在正数前面加上“﹢”,如﹢6,
﹢8,﹢8844···,有时也可省略“﹢”号.
0
﹣3
0
﹢8
像﹣3,﹣2,
﹣155等在正数前面加上“﹣”号的数叫做负数.
负数比0小,负数前面的“﹣”号不可省略.
0
﹣3
0
﹢8
0既不是正数,也不是负数,0是正数和负数的分界.
0
议一议
生活中你见过其他用负数表示的量吗?与同伴进行交流.
说说图中温度和表示方法.
零度,记作0℃
零上5℃,记作﹢5℃
零下5℃,记作﹣5℃
用正、负数表示具有相反意义的量
知识点2
“加分与扣分”
“上涨量与下跌量”
“零上温度与零下温度”
具有相反意义的量
例
(1)
某人转动转盘,
如果用
+5
圈表示沿逆时针方向转了
5
圈,
那么沿顺时针方向转了
12
圈怎样表示?
解:
(1)沿顺时针方向转了
12
圈,
记作
﹣12
圈;
(2)在某次乒乓球质量检测中,
一只乒乓球超出标准质量
0.02
g
记作﹢0.02
g,
那么
﹣0.03
g
表示什么?
解:(2)﹣0.03
g
表示乒乓球的质量低于标准质量
0.03
g;
(3)某大米包装袋上标注着“净含量:
10
kg
±
150
g”,这里的“
10
kg
±
150
g
”
表示什么?
解:
10
kg
-
150
g
≤实际每袋大米质量≤
10
kg
+
150
g
9.85kg
≤实际每袋大米质量≤
10
.15kg
(2)相反意义的量是成对出现的同类量,单独一个量不能称为相反意义的量.
注意:
(1)用正数和负数表示具有相反意义的量时,要根据实际.规定哪种意义的量为正数是任意选择的,那么具有相反意义的量就为负数.
议一议
选定一个高度作为标准,用正负数表示本班每位同学的身高与选定的身高标准的差异.
你是怎样表示的?
与同伴进行交流.
请同学们将所有学过的数进行分类,
并与同伴进行交流.
数的认识
类型
0,1,2,3,···
自然数
4.2,5.2,0.02,···
小数
分数和百分数
﹣3,﹣155,﹣0.4,﹣0.02,···
负数
有理数及其分类
知识点3
,
,50%,3.3%
数的认识
类型
0,1,2,3,···
自然数
4.2,5.2,0.02,···
小数
分数和百分数
﹣3,﹣155,﹣0.4,﹣0.02,···
负数
小数是表示分母是整十、整百的分数.有限小数和无限循环小数也是分数.分数包含了小数和百分数.
正整数
0
分数
负分数
负整数
,
,50%,3.3%
按定义分类:
整数
正整数:如1,2,3···
负整数:如﹣1,
﹣2,
﹣3···
零:0
分数
有理数
整数与分数统称有理数.
负分数:如
,
,-3.5···
正分数:如
,
,5.2···
按符号分类:
正有理数
正整数:如1,2,3···
负整数:如﹣1,﹣2,﹣3···
负有理数
有理数
零:0
正分数:如
,
,5.2···
负分数:如
,
,-3.5···
随堂练习
1.(1)
如果零上
5℃
记作
+5℃,
那么零下
3℃
记作什么?
解:(1)零下3℃记作﹣3℃.
(2)
东、西为两个相反方向,如果-4m表示一个物体向西运动4m,那么+2m表示什么?物体原地不动记作什么?
解:(2)﹢2m表示物体向东运动2m,物体原地不动记作0m.
(3)某仓库运进面粉7.5
t
记作﹢7.5
t,
那么运出面粉3.8
t
应记作什么?
解:(3)运出面粉
3.8
t
应记作﹣3.8
t.
2.
所有的正数组成正数集合,所有的负数组成负数集合,所有的整数组成整数集合,所有的分数组成分数集合.请把下列各数填入相应的集合中:
正数集合:?
···?
负数集合:?
···?
整数集合:?
···?
分数集合:?
···?
3.举出几对具有相反意义的量,并分别用正负数表示.
解:答案不唯一,如球队得10分与失3分,利率上升5%与下降2%,乒乓球超出标准质量0.02g与低于标准质量0.01g,可分别表示为﹢10分与﹣3分,﹢5%与﹣2%,﹢0.02g与﹣0.01g.
4.小丽说:“一个数,
如果不是正数,
必定就是负数.”你认为她说得对吗?为什么?
解:不对,因为0既不是正数,也不是负数.
读一读
在人类生活中,早就存在着收入与支出、赢利与亏本等具有相反意义的现象.中国是最早采用正负数表示相反意义的量,并进行负数运算的国家.有关正负数的概念和运算法则的系统论述,记载于我国古代数学名著《
九章算术》一书中,书中明确提出“正负术”,这是世界上至今发现的最早最详细的记载.公元3世纪,我国数学家刘徽在“正负术”的注文中指出:“今两算得失相反,
要令正、负以名之.正算(筹)赤,负算(筹)黑,否则以邪正为异.”就是说,对两个得失相反的量,要以正、负加以区别.用红筹表示正,黑筹表示负,
也可将算筹正放、斜放来区别.
负数小史
在国外,负数概念的建立和使用,经历了一个曲折的过程.
印度在公元
7
世纪出现了负数概念,并有了负数的运算,不过他们总把负数解释为负债.欧洲的数学家迟迟不承认负数,认为零是最小的数,而比零还小的数是不可思议的.欧洲最早承认负数的是
17
世纪法国数学家笛卡儿(
René
Descartes,
1596-1650),他承认解方程中出现的负根,不过他称之为“假根”.直到
19
世纪,负数在欧洲才获得普遍承认.
课堂小结
有理数
按定义分
按符号分
分类
概念
具有相反意义的量
正数
负数
正数和分数统称有理数
整数
分数
正有理数
负有理数
零
正整数
零
负整数
正分数
负分数
正整数
负整数
正分数
负分数
1.从课后习题中选取,
2.完成练习册本课时的习题.
课后作业
北师大版·七年级上册
第二章
有理数及其运算
1
有理数
观
察
城市
天气
高温
低温
城市
天气
高温
低温
哈尔滨
小雨
15
6
长春
多云
18
10
沈阳
小雨
19
7
天津
小雨
12
8
呼和浩特
雨夹雪
8
﹣3
乌鲁木齐
晴
4
﹣3
西宁
小雪
5
﹣4
银川
小雪
0
﹣3
1.全国主要城市天气预报
同学们可知道天气预报播音员是怎样读这些城市的气温的?
新课导入
高度看作0
2.地形局部示意图
珠穆朗玛峰
8844
m
吐鲁番盆地
﹣155
m
你能说出﹣155表示的实际意义吗,海平面的高度用什么数表示?
探索新知
正数和负数的概念
知识点1
答对
不回答
答错
某班举行知识竞赛,评分标准是:答对一题加1分,答错一题扣1分,不回答得0分;每个队的基本分均为0分.两队答题情况如下表:
扣1分
加1分
现在我们可以用带有“﹢”号和“﹣”号的数表示各队每道题的得分情况.试完成下表:
﹣3
0
﹢8
0
﹣3
0
﹢8
像6,8,8844等比0大的数叫做正数.
有时为了突出数的符号,常在正数前面加上“﹢”,如﹢6,
﹢8,﹢8844···,有时也可省略“﹢”号.
0
﹣3
0
﹢8
像﹣3,﹣2,
﹣155等在正数前面加上“﹣”号的数叫做负数.
负数比0小,负数前面的“﹣”号不可省略.
0
﹣3
0
﹢8
0既不是正数,也不是负数,0是正数和负数的分界.
0
议一议
生活中你见过其他用负数表示的量吗?与同伴进行交流.
说说图中温度和表示方法.
零度,记作0℃
零上5℃,记作﹢5℃
零下5℃,记作﹣5℃
用正、负数表示具有相反意义的量
知识点2
“加分与扣分”
“上涨量与下跌量”
“零上温度与零下温度”
具有相反意义的量
例
(1)
某人转动转盘,
如果用
+5
圈表示沿逆时针方向转了
5
圈,
那么沿顺时针方向转了
12
圈怎样表示?
解:
(1)沿顺时针方向转了
12
圈,
记作
﹣12
圈;
(2)在某次乒乓球质量检测中,
一只乒乓球超出标准质量
0.02
g
记作﹢0.02
g,
那么
﹣0.03
g
表示什么?
解:(2)﹣0.03
g
表示乒乓球的质量低于标准质量
0.03
g;
(3)某大米包装袋上标注着“净含量:
10
kg
±
150
g”,这里的“
10
kg
±
150
g
”
表示什么?
解:
10
kg
-
150
g
≤实际每袋大米质量≤
10
kg
+
150
g
9.85kg
≤实际每袋大米质量≤
10
.15kg
(2)相反意义的量是成对出现的同类量,单独一个量不能称为相反意义的量.
注意:
(1)用正数和负数表示具有相反意义的量时,要根据实际.规定哪种意义的量为正数是任意选择的,那么具有相反意义的量就为负数.
议一议
选定一个高度作为标准,用正负数表示本班每位同学的身高与选定的身高标准的差异.
你是怎样表示的?
与同伴进行交流.
请同学们将所有学过的数进行分类,
并与同伴进行交流.
数的认识
类型
0,1,2,3,···
自然数
4.2,5.2,0.02,···
小数
分数和百分数
﹣3,﹣155,﹣0.4,﹣0.02,···
负数
有理数及其分类
知识点3
,
,50%,3.3%
数的认识
类型
0,1,2,3,···
自然数
4.2,5.2,0.02,···
小数
分数和百分数
﹣3,﹣155,﹣0.4,﹣0.02,···
负数
小数是表示分母是整十、整百的分数.有限小数和无限循环小数也是分数.分数包含了小数和百分数.
正整数
0
分数
负分数
负整数
,
,50%,3.3%
按定义分类:
整数
正整数:如1,2,3···
负整数:如﹣1,
﹣2,
﹣3···
零:0
分数
有理数
整数与分数统称有理数.
负分数:如
,
,-3.5···
正分数:如
,
,5.2···
按符号分类:
正有理数
正整数:如1,2,3···
负整数:如﹣1,﹣2,﹣3···
负有理数
有理数
零:0
正分数:如
,
,5.2···
负分数:如
,
,-3.5···
随堂练习
1.(1)
如果零上
5℃
记作
+5℃,
那么零下
3℃
记作什么?
解:(1)零下3℃记作﹣3℃.
(2)
东、西为两个相反方向,如果-4m表示一个物体向西运动4m,那么+2m表示什么?物体原地不动记作什么?
解:(2)﹢2m表示物体向东运动2m,物体原地不动记作0m.
(3)某仓库运进面粉7.5
t
记作﹢7.5
t,
那么运出面粉3.8
t
应记作什么?
解:(3)运出面粉
3.8
t
应记作﹣3.8
t.
2.
所有的正数组成正数集合,所有的负数组成负数集合,所有的整数组成整数集合,所有的分数组成分数集合.请把下列各数填入相应的集合中:
正数集合:?
···?
负数集合:?
···?
整数集合:?
···?
分数集合:?
···?
3.举出几对具有相反意义的量,并分别用正负数表示.
解:答案不唯一,如球队得10分与失3分,利率上升5%与下降2%,乒乓球超出标准质量0.02g与低于标准质量0.01g,可分别表示为﹢10分与﹣3分,﹢5%与﹣2%,﹢0.02g与﹣0.01g.
4.小丽说:“一个数,
如果不是正数,
必定就是负数.”你认为她说得对吗?为什么?
解:不对,因为0既不是正数,也不是负数.
读一读
在人类生活中,早就存在着收入与支出、赢利与亏本等具有相反意义的现象.中国是最早采用正负数表示相反意义的量,并进行负数运算的国家.有关正负数的概念和运算法则的系统论述,记载于我国古代数学名著《
九章算术》一书中,书中明确提出“正负术”,这是世界上至今发现的最早最详细的记载.公元3世纪,我国数学家刘徽在“正负术”的注文中指出:“今两算得失相反,
要令正、负以名之.正算(筹)赤,负算(筹)黑,否则以邪正为异.”就是说,对两个得失相反的量,要以正、负加以区别.用红筹表示正,黑筹表示负,
也可将算筹正放、斜放来区别.
负数小史
在国外,负数概念的建立和使用,经历了一个曲折的过程.
印度在公元
7
世纪出现了负数概念,并有了负数的运算,不过他们总把负数解释为负债.欧洲的数学家迟迟不承认负数,认为零是最小的数,而比零还小的数是不可思议的.欧洲最早承认负数的是
17
世纪法国数学家笛卡儿(
René
Descartes,
1596-1650),他承认解方程中出现的负根,不过他称之为“假根”.直到
19
世纪,负数在欧洲才获得普遍承认.
课堂小结
有理数
按定义分
按符号分
分类
概念
具有相反意义的量
正数
负数
正数和分数统称有理数
整数
分数
正有理数
负有理数
零
正整数
零
负整数
正分数
负分数
正整数
负整数
正分数
负分数
1.从课后习题中选取,
2.完成练习册本课时的习题.
课后作业
同课章节目录
- 第一章 丰富的图形世界
- 1.1 生活中的立体图形
- 1.2 展开与折叠
- 1.3 截一个几何体
- 1.4 从三个不同方向看物体的形状
- 第二章 有理数及其运算
- 2.1 有理数
- 2.2 数轴
- 2.3 绝对值
- 2.4 有理数的加法
- 2.5 有理数的减法
- 2.6 有理数的加减混合运算
- 2.7 有理数的乘法
- 2.8 有理数的除法
- 2.9 有理数的乘方
- 2.10 科学记数法
- 2.11 有理数的混合运算
- 2.12 用计算器进行运算
- 第三章 整式及其加减
- 3.1 字母表示数
- 3.2 代数式
- 3.3 整式
- 3.4 整式的加减
- 3.5 探索与表达规律
- 第四章 基本平面图形
- 4.1 线段、射线、直线
- 4.2 比较线段的长短
- 4.3 角
- 4.4 角的比较
- 4.5 多边形和圆的初步认识
- 第五章 一元一次方程
- 5.1 认识一元一次方程
- 5.2 求解一元一次方程
- 5.3 应用一元一次方程——水箱变高了
- 5.4 应用一元一次方程——打折销售
- 5.5 应用一元一次方程——“希望工程”义演
- 5.6 应用一元一次方程——追赶小明
- 第六章 数据的收集与整理
- 6.1 数据的收集
- 6.2 普查和抽样调查
- 6.3 数据的表示
- 6.4 统计图的选择
