海南省部分学校2020-2021学年高一下学期期末考试数学试题 Word版含答案
文档属性
| 名称 | 海南省部分学校2020-2021学年高一下学期期末考试数学试题 Word版含答案 |  | |
| 格式 | docx | ||
| 文件大小 | 630.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-06 20:58:33 | ||
图片预览



文档简介
海南省2020—2021学年第二学期高一期末考试
数学
一、单项选择题
1.false( ).
A.false B.false C.false D.false
2.某射击运动员连续射击5次,射中环数分别为7,7,8,9,9,则这5次射中环数的方差为( ).
A.0.8 B.1 C.1.2 D.1.6
3.已知正六边形false的边长为1,则false( ).
A.false B.false C.false D.1
4.设向量false,false,且向量false与false共线,则false( ).
A.false B.false C.false D.false
5.已知false,且false,则false( ).
A.false B.false C.false D.false
6.将一个大圆锥截去一个小圆锥得到圆台,圆台的上、下底面圆的半径之比为false,若大圆锥的高为2,则圆台的高为( ).
A.6 B.8 C.9 D.10
7.甲、乙、丙三个社区居民的人数之比为false,新冠疫苗接种率分别为false,false,false,则这三个社区的居民总体的新冠疫苗接种率为( ).
A.false B.false C.false D.false
8.已知长方体false的底面是边长为4的正方形其外接球的表面积为false,则异面直线false与false所成的角的余弦值为( ).
A.false B.false C.false D.false
二、多项选择题
9.已知复数false,则( ).
A.false的虚部为false B.false在复平面内对应的点位于第二象限
C.false D.false
10.已知平面false,false互相平行,直线false,false满足false,false,则( ).
A.false B.false C.false D.false
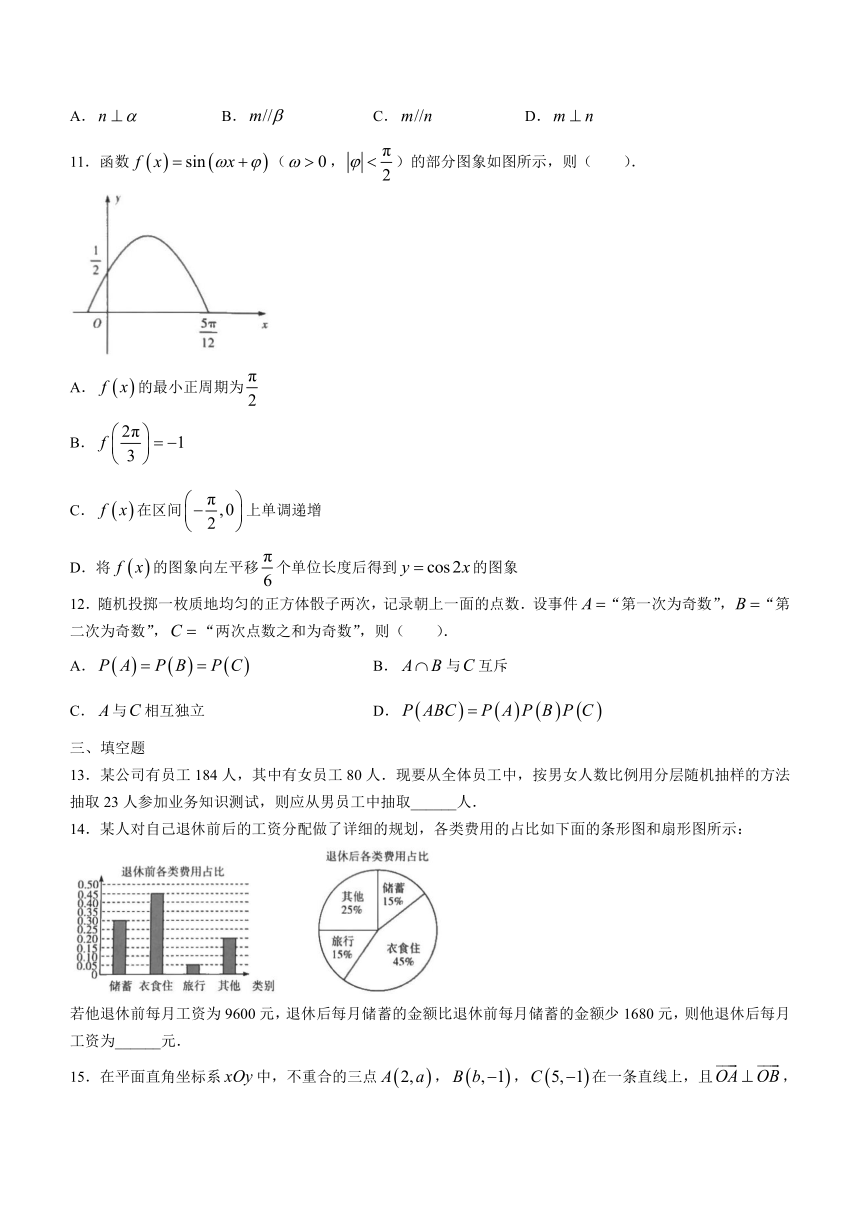
11.函数false(false,false)的部分图象如图所示,则( ).
A.false的最小正周期为false
B.false
C.false在区间false上单调递增
D.将false的图象向左平移false个单位长度后得到false的图象
12.随机投掷一枚质地均匀的正方体骰子两次,记录朝上一面的点数.设事件false“第一次为奇数”,false“第二次为奇数”,false“两次点数之和为奇数”,则( ).
A.false B.false与false互斥
C.false与false相互独立 D.false
三、填空题
13.某公司有员工184人,其中有女员工80人.现要从全体员工中,按男女人数比例用分层随机抽样的方法抽取23人参加业务知识测试,则应从男员工中抽取______人.
14.某人对自己退休前后的工资分配做了详细的规划,各类费用的占比如下面的条形图和扇形图所示:
若他退休前每月工资为9600元,退休后每月储蓄的金额比退休前每月储蓄的金额少1680元,则他退休后每月工资为______元.
15.在平面直角坐标系false中,不重合的三点false,false,false在一条直线上,且false,则false______.
16.某球类比赛的冠军奖杯如图所示,顶部的球通过三根竖直的支撑杆与水平放置的长方体底座相连.若球的半径为false,三根支撑杆长度均为false,粗细忽略不计,且任意两根支撑杆之间的距离均为false,则球的最低点到底座上表面的距离为________false.
四、解答题
17.某电影院统计了该影院今年上半年上映的电影的有关数据,得到如下表格:
电影类型
动作
科幻
喜剧
爱情
其他
电影部数
10
5
15
20
10
好评率
0.6
0.4
0.4
0.25
0.2
好评率是指:一类电影中获得好评的部数与该类电影的部数的比值.若从该影院今年上半年上映的所有电影中随机选1部.
(1)求这部电影是获得好评的喜剧电影的概率;
(2)求这部电影没有获得好评的概率.
18.已知函数false.
(1)求false的值域;
(2)求false的零点的集合.
19.如图所示,正方形false所在的平面与梯形false所在的平面垂直,false,且false,点false为线段false的中点.
(1)证明:false平面false;
(2)若false,false,求直线false与平面false所成角的正切值.
20.如图所示,三棱柱false中,false,false,false,false.
(1)证明:false;
(2)若false,求三棱柱false的体积.
21.某机械零件工厂为了检验产品的质量,质检部门随机在生产线上抽取了100个零件并称出它们的重量(单位:克).重量按照false,false,…,false分组,得到频率分布直方图如图所示.
(1)估计该工厂生产的零件重量的平均数;(每组数据用该组的中点值作代表)
(2)估计该工厂生产的零件重量的false分位数;
(3)按各组零件数量比例用分层随机抽样方法从样本里重量不低于525克的零件中抽取6个零件,再从这6个零件中任取2个,求这2个零件的重量均在false内的概率.
22.在false中,内角false,false,false所对的边分别为false,false,false,已知false.
(1)求角false;
(2)若false且false是锐角三角形,求false的面积的取值范围.
答案
1.【答案】A
【解析】
2.【答案】A
【解析】
3.【答案】D
【解析】
4.【答案】C
【解析】
5.【答案】B
【解析】
6.【答案】B
【解析】
7.【答案】C
【解析】
8.【答案】C
【解析】
9.【答案】CD
【解析】
10.【答案】AD
【解析】
11.【答案】BD
【解析】
12.【答案】ABC
【解析】
13.【答案】13
【解析】
14.【答案】8000
【解析】
15.【答案】false
【解析】
16.【答案】24
【解析】
17.【答案】(1)总的电影部数为false,
获得好评的喜剧电影有false部.
故这部电影是获得好评的喜剧电影的概率为false.
(2)获得好评的电影部数为false.
这部电影获得好评的概率为false,
故这部电影没有获得好评的概率为false.
【解析】
18.【答案】(1)由题可知false
false.
∵false,
∴false,
即false的值域为false.
(2)令false,得false,
∴false或false,false,
∴false或false,false,
∴false的零点的集合为false.
【解析】
19.【答案】(1)如图,连接false,设false与false的交点为false,连接false,
则false为false的中点,又因为false是false的中点,所以false,
因为false平面false,false平面false,所以false平面false.
(2)过false作false,垂足为false,连接false.
因为平面false平面false,交线为false,false平面false,
所以false平面false.
因此false为直线false与平面false所成的角.
因为false,false,false,
所以false,false,false.
所以false,
故false,
即false与平面false所成角的正切值为false.
【解析】
20.【答案】(1)∵false,false,false.
∴false,∴false.
∵false,false,∴false.
又∵false,∴false平面false.
∵false平面false,∴false.
(2)∵false,false,false,
∴false,∴false,∴false,
由(1)可得false,false,∴false平面false.
∴false.
【解析】
21.【答案】(1)根据题意,false,
解之得false.
各个小组的频率分别为0.15,0.2,0.35,0.25,0.05.
估计该工厂生产的零件重量的平均数约为false.
(2)设false分位数为false,因为前三组频率和为0.7,前四组频率和为0.95,所以false,
因此,可估计该工厂生产的零件重量的false分位数约为false.
(3)由条件知6个零件中,重量在false内的零件个数为5,分别记为false,false,false,false,false;重量在false内的零件个数为1,记为false.
从中随机抽取2个,样本空间为falsefalse,所以false.
设“这2个零件的重量均在false内”为事件false,
则false,false,
所以false.
【解析】
22.【答案】(1)由false及正弦定理,
得false,即false,
再由余弦定理可得false,
因为false,所以false.
(2)false.
由正弦定理可知false,又false,
所以false,
因为false是锐角三角形,故false,false,
所以false,所以false,从而false,
故false,
即false的面积的取值范围是false.
【解析】
数学
一、单项选择题
1.false( ).
A.false B.false C.false D.false
2.某射击运动员连续射击5次,射中环数分别为7,7,8,9,9,则这5次射中环数的方差为( ).
A.0.8 B.1 C.1.2 D.1.6
3.已知正六边形false的边长为1,则false( ).
A.false B.false C.false D.1
4.设向量false,false,且向量false与false共线,则false( ).
A.false B.false C.false D.false
5.已知false,且false,则false( ).
A.false B.false C.false D.false
6.将一个大圆锥截去一个小圆锥得到圆台,圆台的上、下底面圆的半径之比为false,若大圆锥的高为2,则圆台的高为( ).
A.6 B.8 C.9 D.10
7.甲、乙、丙三个社区居民的人数之比为false,新冠疫苗接种率分别为false,false,false,则这三个社区的居民总体的新冠疫苗接种率为( ).
A.false B.false C.false D.false
8.已知长方体false的底面是边长为4的正方形其外接球的表面积为false,则异面直线false与false所成的角的余弦值为( ).
A.false B.false C.false D.false
二、多项选择题
9.已知复数false,则( ).
A.false的虚部为false B.false在复平面内对应的点位于第二象限
C.false D.false
10.已知平面false,false互相平行,直线false,false满足false,false,则( ).
A.false B.false C.false D.false
11.函数false(false,false)的部分图象如图所示,则( ).
A.false的最小正周期为false
B.false
C.false在区间false上单调递增
D.将false的图象向左平移false个单位长度后得到false的图象
12.随机投掷一枚质地均匀的正方体骰子两次,记录朝上一面的点数.设事件false“第一次为奇数”,false“第二次为奇数”,false“两次点数之和为奇数”,则( ).
A.false B.false与false互斥
C.false与false相互独立 D.false
三、填空题
13.某公司有员工184人,其中有女员工80人.现要从全体员工中,按男女人数比例用分层随机抽样的方法抽取23人参加业务知识测试,则应从男员工中抽取______人.
14.某人对自己退休前后的工资分配做了详细的规划,各类费用的占比如下面的条形图和扇形图所示:
若他退休前每月工资为9600元,退休后每月储蓄的金额比退休前每月储蓄的金额少1680元,则他退休后每月工资为______元.
15.在平面直角坐标系false中,不重合的三点false,false,false在一条直线上,且false,则false______.
16.某球类比赛的冠军奖杯如图所示,顶部的球通过三根竖直的支撑杆与水平放置的长方体底座相连.若球的半径为false,三根支撑杆长度均为false,粗细忽略不计,且任意两根支撑杆之间的距离均为false,则球的最低点到底座上表面的距离为________false.
四、解答题
17.某电影院统计了该影院今年上半年上映的电影的有关数据,得到如下表格:
电影类型
动作
科幻
喜剧
爱情
其他
电影部数
10
5
15
20
10
好评率
0.6
0.4
0.4
0.25
0.2
好评率是指:一类电影中获得好评的部数与该类电影的部数的比值.若从该影院今年上半年上映的所有电影中随机选1部.
(1)求这部电影是获得好评的喜剧电影的概率;
(2)求这部电影没有获得好评的概率.
18.已知函数false.
(1)求false的值域;
(2)求false的零点的集合.
19.如图所示,正方形false所在的平面与梯形false所在的平面垂直,false,且false,点false为线段false的中点.
(1)证明:false平面false;
(2)若false,false,求直线false与平面false所成角的正切值.
20.如图所示,三棱柱false中,false,false,false,false.
(1)证明:false;
(2)若false,求三棱柱false的体积.
21.某机械零件工厂为了检验产品的质量,质检部门随机在生产线上抽取了100个零件并称出它们的重量(单位:克).重量按照false,false,…,false分组,得到频率分布直方图如图所示.
(1)估计该工厂生产的零件重量的平均数;(每组数据用该组的中点值作代表)
(2)估计该工厂生产的零件重量的false分位数;
(3)按各组零件数量比例用分层随机抽样方法从样本里重量不低于525克的零件中抽取6个零件,再从这6个零件中任取2个,求这2个零件的重量均在false内的概率.
22.在false中,内角false,false,false所对的边分别为false,false,false,已知false.
(1)求角false;
(2)若false且false是锐角三角形,求false的面积的取值范围.
答案
1.【答案】A
【解析】
2.【答案】A
【解析】
3.【答案】D
【解析】
4.【答案】C
【解析】
5.【答案】B
【解析】
6.【答案】B
【解析】
7.【答案】C
【解析】
8.【答案】C
【解析】
9.【答案】CD
【解析】
10.【答案】AD
【解析】
11.【答案】BD
【解析】
12.【答案】ABC
【解析】
13.【答案】13
【解析】
14.【答案】8000
【解析】
15.【答案】false
【解析】
16.【答案】24
【解析】
17.【答案】(1)总的电影部数为false,
获得好评的喜剧电影有false部.
故这部电影是获得好评的喜剧电影的概率为false.
(2)获得好评的电影部数为false.
这部电影获得好评的概率为false,
故这部电影没有获得好评的概率为false.
【解析】
18.【答案】(1)由题可知false
false.
∵false,
∴false,
即false的值域为false.
(2)令false,得false,
∴false或false,false,
∴false或false,false,
∴false的零点的集合为false.
【解析】
19.【答案】(1)如图,连接false,设false与false的交点为false,连接false,
则false为false的中点,又因为false是false的中点,所以false,
因为false平面false,false平面false,所以false平面false.
(2)过false作false,垂足为false,连接false.
因为平面false平面false,交线为false,false平面false,
所以false平面false.
因此false为直线false与平面false所成的角.
因为false,false,false,
所以false,false,false.
所以false,
故false,
即false与平面false所成角的正切值为false.
【解析】
20.【答案】(1)∵false,false,false.
∴false,∴false.
∵false,false,∴false.
又∵false,∴false平面false.
∵false平面false,∴false.
(2)∵false,false,false,
∴false,∴false,∴false,
由(1)可得false,false,∴false平面false.
∴false.
【解析】
21.【答案】(1)根据题意,false,
解之得false.
各个小组的频率分别为0.15,0.2,0.35,0.25,0.05.
估计该工厂生产的零件重量的平均数约为false.
(2)设false分位数为false,因为前三组频率和为0.7,前四组频率和为0.95,所以false,
因此,可估计该工厂生产的零件重量的false分位数约为false.
(3)由条件知6个零件中,重量在false内的零件个数为5,分别记为false,false,false,false,false;重量在false内的零件个数为1,记为false.
从中随机抽取2个,样本空间为falsefalse,所以false.
设“这2个零件的重量均在false内”为事件false,
则false,false,
所以false.
【解析】
22.【答案】(1)由false及正弦定理,
得false,即false,
再由余弦定理可得false,
因为false,所以false.
(2)false.
由正弦定理可知false,又false,
所以false,
因为false是锐角三角形,故false,false,
所以false,所以false,从而false,
故false,
即false的面积的取值范围是false.
【解析】
同课章节目录
