安徽省太湖中学2011-2012学年高二下学期期中考试数学(文)试题
文档属性
| 名称 | 安徽省太湖中学2011-2012学年高二下学期期中考试数学(文)试题 |  | |
| 格式 | zip | ||
| 文件大小 | 231.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-04-24 20:48:13 | ||
图片预览


文档简介
独立性检验:独立性检验统计量,其中
概率表
0.005 0.001
7.879 10.828
一、选择题(本大题共10小题,每小题5分,共50分,在每小题给出的四个选项中,只有一项是符合题目要求的。请把答案写在答卷相应的位置上)
1、复数的实部是( )
A.2 B.1 C. D.
2、下列命题中正确的是( )
A.类比推理是一般到特殊的推理 B.演绎推理的结论一定是正确的
C.合情推理的结论一定是正确的
D.演绎推理在前提和推理形式都正确的前提下,得到的结论一定是正确的
3、下列命题中的假命题是( )
A. x∈R,lg x=0 B. x∈R,tan x=1 C. x∈R,x3>0 D. x∈R,2x>0
4、有一段“三段论”推理是这样的:对于可导函数,如果,那么是函数的极值点,因为函数在处的导数值,所以,是函数的极值点.以上推理中( )
A.大前提错误 B. 小前提错误 C.推理形式错误 D.结论正确
5、由一组样本数据(x1,y1),(x2,y2),…(xn,yn)得到的回归直线,那么下面说法不正确的是( )
A.直线必经过点(,)
B.直线至少经过点(x1,y1), (x2,y2), …(xn,yn)中的一个点
C.直线的斜率为
D.直线和各点(x1,y1),(), …(xn,yn)的偏差和
是该坐标平面上所有直线与这些点的偏差和中最小的直线
6、在吸烟与患肺病这两个分类变量的计算中,下列说法正确的是( )
A.若K2的观测值为k=6.635,在犯错误的概率不超过的前提下认为吸烟与患肺病有关系,那么在100个吸烟的人中必有99人患有肺病;
B.由独立性检验可知,在犯错误的概率不超过的前提下认为吸烟与患肺病有关系,我们说某人吸烟,那么他有99%的可能患有肺病;
C.若从统计量中求出在犯错误的概率不超过的前提下认为吸烟与
患肺病有关系,是指有1% 的可能性使得判断出现错误;
D.以上三种说法都不正确.
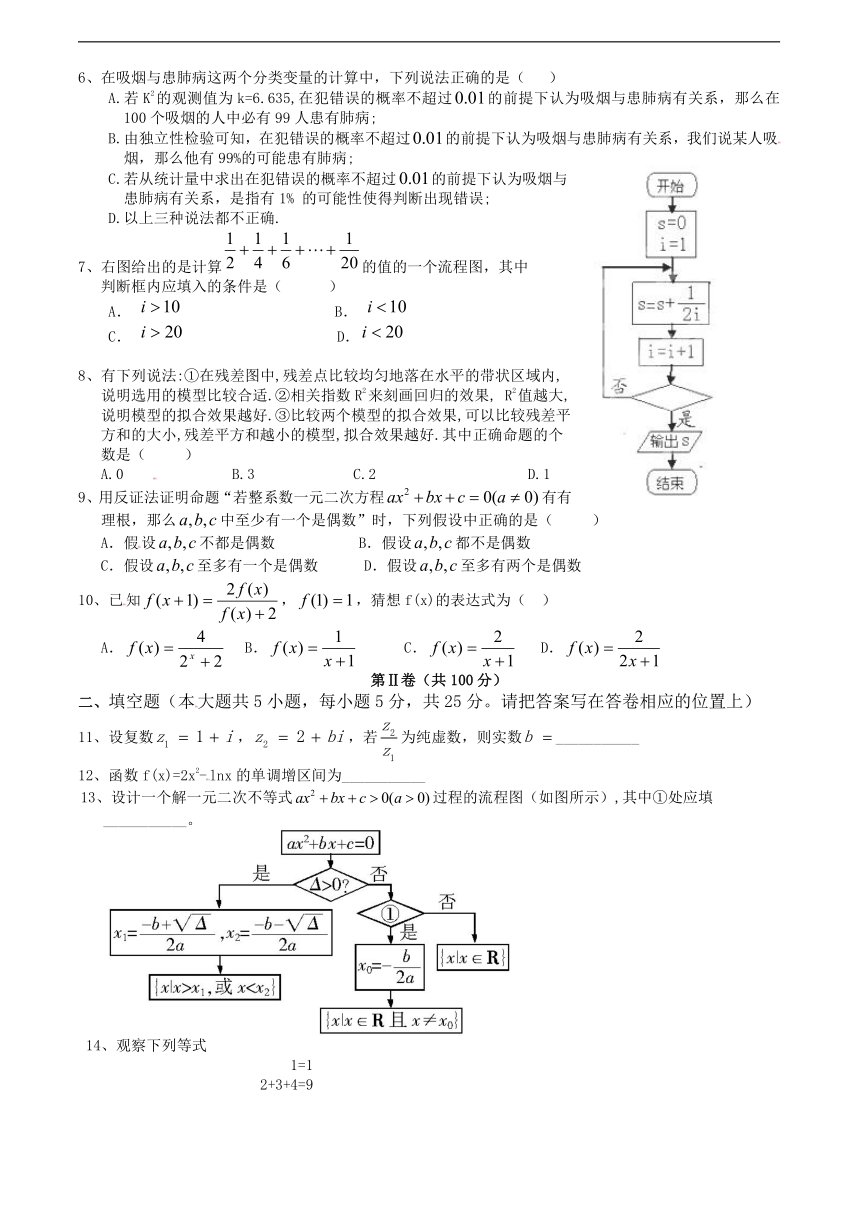
7、右图给出的是计算的值的一个流程图,其中
判断框内应填入的条件是( )
A. B.
C. D.
8、有下列说法:①在残差图中,残差点比较均匀地落在水平的带状区域内,
说明选用的模型比较合适.②相关指数R2来刻画回归的效果, R2值越大,
说明模型的拟合效果越好.③比较两个模型的拟合效果,可以比较残差平
方和的大小,残差平方和越小的模型,拟合效果越好.其中正确命题的个
数是( )
A.0 B.3 C.2 D.1
9、用反证法证明命题“若整系数一元二次方程有有
理根,那么中至少有一个是偶数”时,下列假设中正确的是( )
A.假设不都是偶数 B.假设都不是偶数
C.假设至多有一个是偶数 D.假设至多有两个是偶数
10、已知,,猜想f(x)的表达式为( )
A. B. C. D.
第Ⅱ卷(共100分)
二、填空题(本大题共5小题,每小题5分,共25分。请把答案写在答卷相应的位置上)
11、设复数,,若为纯虚数,则实数___________
12、函数f(x)=2x2-lnx的单调增区间为___________
13、设计一个解一元二次不等式过程的流程图(如图所示),其中①处应填___________。
14、观察下列等式
1=1
2+3+4=9
3+4+5+6+7=25
4+5+6+7+8+9+10=49
照此规律,第n个等式应为__________________.
15、有下列四个命题:
①、命题“若,则,互为倒数”的逆命题; ②、命题“面积相等的三角形全等”的否命题;③、命题“若,则有实根”的逆否命题; ④、命题“若,则”的逆否命题。
其中是真命题的是 (填上你认为正确的命题的序号)
三、解答题 (本大题共75分,解答应写出必要的文字说明)
16. (本小题12分)已知复数z=(2+i)(i-3)+4-2i;
(1)求复数z的共轭复数及||;
(2)设复数z1=(a2-2a)+ai是纯虚数,求实数a的值。
17、(本小题12分).假设关于某设备的使用年限x和所支出的维修费用y(万元),有如下的统计资料:
x 2 3 4 5 6
y 2.2 3.8 5.5 6.5 7.0
若由资料可知y对x呈线性相关关系。试求:
(1)线性回归方程;
(2)估计使用年限为10年时,维修费用是多少?
18、(本小题12分)试比较下列各式的大小(不写过程)
(1)与
(2)与
通过上式请你推测出与且n的大小,并用分析法加以证明。
19、(本小题12分))为调查某地区老年人是否需要志愿者提供帮助,用简单随机抽样方法从该地区调查了500位老年人,结果如下:
性别是否需要志愿者 男 女
需要 40 30
不需要 160 270
(1)估计该地区老年人中,需要志愿者提供帮助的老年人的比例;
(2)能否有99%的把握认为该地区的老年人是否需要志愿者提供帮助与性别有关?
(3)根据(2)的结论,能否提出更好的调查方法来估计该地区的老年人中需要志愿者提供帮助的老年人的比例?说明理由.
20、(本小题13分)如图,在正三棱柱ABC—A1B1C1中,AB=AA1,点D是A1B1的中点,点F是AB的中点,点E在A1C1上,且DE⊥AE。
(1)证明B1F//平面ADE;
(2)证明平面ABC1⊥平面C1DF;
(3)求直线AD和平面ABC1所成角的正弦值。
21、(本小题14分)设函数,
(Ⅰ)求的定义域; (Ⅱ)求的单调增区间和减区间;
(Ⅲ) 求所有实数,使对恒成立.
安徽省太湖中学2011-2012学年第二学期期中考试
高二数学(文科)试题参考答案
选择题(每小题5分,共50分)
1 2 3 4 5 6 7 8 9 10
C D C A B C A B B C
二、填空题(每小题5分,共25分)
11.-2 12. () 13. 14. 15.①
三、解答题:(本大题共6小题,共75分,解答应写出文字说明、证明过程或演算步骤。)
16解:(1)Z=-3-3i =-3+3i ||=3 (6分)
(2) a=2 (12分)
17. 解:(1)列表如下:
i 1 2 3 4 5
2 3 4 5 6
2.2 3.8 5.5 6.5 7.0
4.4 11.4 22.0 32.5 42.0
4 9 16 25 36
,,
要帮助的老年人的比例的估计值为=14%. (4分)
(2)K2的观测值,因为9.967>6.635,所以有99%的把握认为该地区的老年人是否需要志愿者提供帮助与性别有关. (8分)
(3)根据(2)的结论可知,该地区的老年人是否需要志愿者提供帮助与性别有关,并且从样本数据能够看出该地区男性老年人与女性老年人中需要帮助的比例有明显差异,因此在调查时,先确定该地区老年人中男女的比例,再把老年人分成男女两层,并采用分层抽样方法比简单随机抽样方法更好. (12分)
20. (本小题13分)(1)证明: 如图所示,在正三棱柱中, D是的中点,点F是AB的中点,所以,且,所以四边形是平行四边形,所以, AD在平面ADE内,不在平面ADE内, 故. (4分)
(2)证明:如图所示,F是AB的中点,连接DF、DC、CF,由正三棱柱ABC- ABC的性质及D是AB的中点知,,又CDDF=D,所以AB平面CDF,而AB∥AB,所以AB平面CDF,又AB平面ABC,故平面AB C平面CDF。 (8分)
(3)解: 过点D作DH垂直CF于点H,则DH平面ABC.连接AH,则HAD是AD和平面ABC所成的角。由已知AB=A A,不妨设
成角的正弦值为。 (13分)
概率表
0.005 0.001
7.879 10.828
一、选择题(本大题共10小题,每小题5分,共50分,在每小题给出的四个选项中,只有一项是符合题目要求的。请把答案写在答卷相应的位置上)
1、复数的实部是( )
A.2 B.1 C. D.
2、下列命题中正确的是( )
A.类比推理是一般到特殊的推理 B.演绎推理的结论一定是正确的
C.合情推理的结论一定是正确的
D.演绎推理在前提和推理形式都正确的前提下,得到的结论一定是正确的
3、下列命题中的假命题是( )
A. x∈R,lg x=0 B. x∈R,tan x=1 C. x∈R,x3>0 D. x∈R,2x>0
4、有一段“三段论”推理是这样的:对于可导函数,如果,那么是函数的极值点,因为函数在处的导数值,所以,是函数的极值点.以上推理中( )
A.大前提错误 B. 小前提错误 C.推理形式错误 D.结论正确
5、由一组样本数据(x1,y1),(x2,y2),…(xn,yn)得到的回归直线,那么下面说法不正确的是( )
A.直线必经过点(,)
B.直线至少经过点(x1,y1), (x2,y2), …(xn,yn)中的一个点
C.直线的斜率为
D.直线和各点(x1,y1),(), …(xn,yn)的偏差和
是该坐标平面上所有直线与这些点的偏差和中最小的直线
6、在吸烟与患肺病这两个分类变量的计算中,下列说法正确的是( )
A.若K2的观测值为k=6.635,在犯错误的概率不超过的前提下认为吸烟与患肺病有关系,那么在100个吸烟的人中必有99人患有肺病;
B.由独立性检验可知,在犯错误的概率不超过的前提下认为吸烟与患肺病有关系,我们说某人吸烟,那么他有99%的可能患有肺病;
C.若从统计量中求出在犯错误的概率不超过的前提下认为吸烟与
患肺病有关系,是指有1% 的可能性使得判断出现错误;
D.以上三种说法都不正确.
7、右图给出的是计算的值的一个流程图,其中
判断框内应填入的条件是( )
A. B.
C. D.
8、有下列说法:①在残差图中,残差点比较均匀地落在水平的带状区域内,
说明选用的模型比较合适.②相关指数R2来刻画回归的效果, R2值越大,
说明模型的拟合效果越好.③比较两个模型的拟合效果,可以比较残差平
方和的大小,残差平方和越小的模型,拟合效果越好.其中正确命题的个
数是( )
A.0 B.3 C.2 D.1
9、用反证法证明命题“若整系数一元二次方程有有
理根,那么中至少有一个是偶数”时,下列假设中正确的是( )
A.假设不都是偶数 B.假设都不是偶数
C.假设至多有一个是偶数 D.假设至多有两个是偶数
10、已知,,猜想f(x)的表达式为( )
A. B. C. D.
第Ⅱ卷(共100分)
二、填空题(本大题共5小题,每小题5分,共25分。请把答案写在答卷相应的位置上)
11、设复数,,若为纯虚数,则实数___________
12、函数f(x)=2x2-lnx的单调增区间为___________
13、设计一个解一元二次不等式过程的流程图(如图所示),其中①处应填___________。
14、观察下列等式
1=1
2+3+4=9
3+4+5+6+7=25
4+5+6+7+8+9+10=49
照此规律,第n个等式应为__________________.
15、有下列四个命题:
①、命题“若,则,互为倒数”的逆命题; ②、命题“面积相等的三角形全等”的否命题;③、命题“若,则有实根”的逆否命题; ④、命题“若,则”的逆否命题。
其中是真命题的是 (填上你认为正确的命题的序号)
三、解答题 (本大题共75分,解答应写出必要的文字说明)
16. (本小题12分)已知复数z=(2+i)(i-3)+4-2i;
(1)求复数z的共轭复数及||;
(2)设复数z1=(a2-2a)+ai是纯虚数,求实数a的值。
17、(本小题12分).假设关于某设备的使用年限x和所支出的维修费用y(万元),有如下的统计资料:
x 2 3 4 5 6
y 2.2 3.8 5.5 6.5 7.0
若由资料可知y对x呈线性相关关系。试求:
(1)线性回归方程;
(2)估计使用年限为10年时,维修费用是多少?
18、(本小题12分)试比较下列各式的大小(不写过程)
(1)与
(2)与
通过上式请你推测出与且n的大小,并用分析法加以证明。
19、(本小题12分))为调查某地区老年人是否需要志愿者提供帮助,用简单随机抽样方法从该地区调查了500位老年人,结果如下:
性别是否需要志愿者 男 女
需要 40 30
不需要 160 270
(1)估计该地区老年人中,需要志愿者提供帮助的老年人的比例;
(2)能否有99%的把握认为该地区的老年人是否需要志愿者提供帮助与性别有关?
(3)根据(2)的结论,能否提出更好的调查方法来估计该地区的老年人中需要志愿者提供帮助的老年人的比例?说明理由.
20、(本小题13分)如图,在正三棱柱ABC—A1B1C1中,AB=AA1,点D是A1B1的中点,点F是AB的中点,点E在A1C1上,且DE⊥AE。
(1)证明B1F//平面ADE;
(2)证明平面ABC1⊥平面C1DF;
(3)求直线AD和平面ABC1所成角的正弦值。
21、(本小题14分)设函数,
(Ⅰ)求的定义域; (Ⅱ)求的单调增区间和减区间;
(Ⅲ) 求所有实数,使对恒成立.
安徽省太湖中学2011-2012学年第二学期期中考试
高二数学(文科)试题参考答案
选择题(每小题5分,共50分)
1 2 3 4 5 6 7 8 9 10
C D C A B C A B B C
二、填空题(每小题5分,共25分)
11.-2 12. () 13. 14. 15.①
三、解答题:(本大题共6小题,共75分,解答应写出文字说明、证明过程或演算步骤。)
16解:(1)Z=-3-3i =-3+3i ||=3 (6分)
(2) a=2 (12分)
17. 解:(1)列表如下:
i 1 2 3 4 5
2 3 4 5 6
2.2 3.8 5.5 6.5 7.0
4.4 11.4 22.0 32.5 42.0
4 9 16 25 36
,,
要帮助的老年人的比例的估计值为=14%. (4分)
(2)K2的观测值,因为9.967>6.635,所以有99%的把握认为该地区的老年人是否需要志愿者提供帮助与性别有关. (8分)
(3)根据(2)的结论可知,该地区的老年人是否需要志愿者提供帮助与性别有关,并且从样本数据能够看出该地区男性老年人与女性老年人中需要帮助的比例有明显差异,因此在调查时,先确定该地区老年人中男女的比例,再把老年人分成男女两层,并采用分层抽样方法比简单随机抽样方法更好. (12分)
20. (本小题13分)(1)证明: 如图所示,在正三棱柱中, D是的中点,点F是AB的中点,所以,且,所以四边形是平行四边形,所以, AD在平面ADE内,不在平面ADE内, 故. (4分)
(2)证明:如图所示,F是AB的中点,连接DF、DC、CF,由正三棱柱ABC- ABC的性质及D是AB的中点知,,又CDDF=D,所以AB平面CDF,而AB∥AB,所以AB平面CDF,又AB平面ABC,故平面AB C平面CDF。 (8分)
(3)解: 过点D作DH垂直CF于点H,则DH平面ABC.连接AH,则HAD是AD和平面ABC所成的角。由已知AB=A A,不妨设
成角的正弦值为。 (13分)
同课章节目录
