2021_2022学年八年级数学上册第14章勾股定理14.1.1第2课时勾股定理的简单应用练习题新版华东师大版
文档属性
| 名称 | 2021_2022学年八年级数学上册第14章勾股定理14.1.1第2课时勾股定理的简单应用练习题新版华东师大版 |
|
|
| 格式 | doc | ||
| 文件大小 | 382.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-07 00:00:00 | ||
图片预览

文档简介
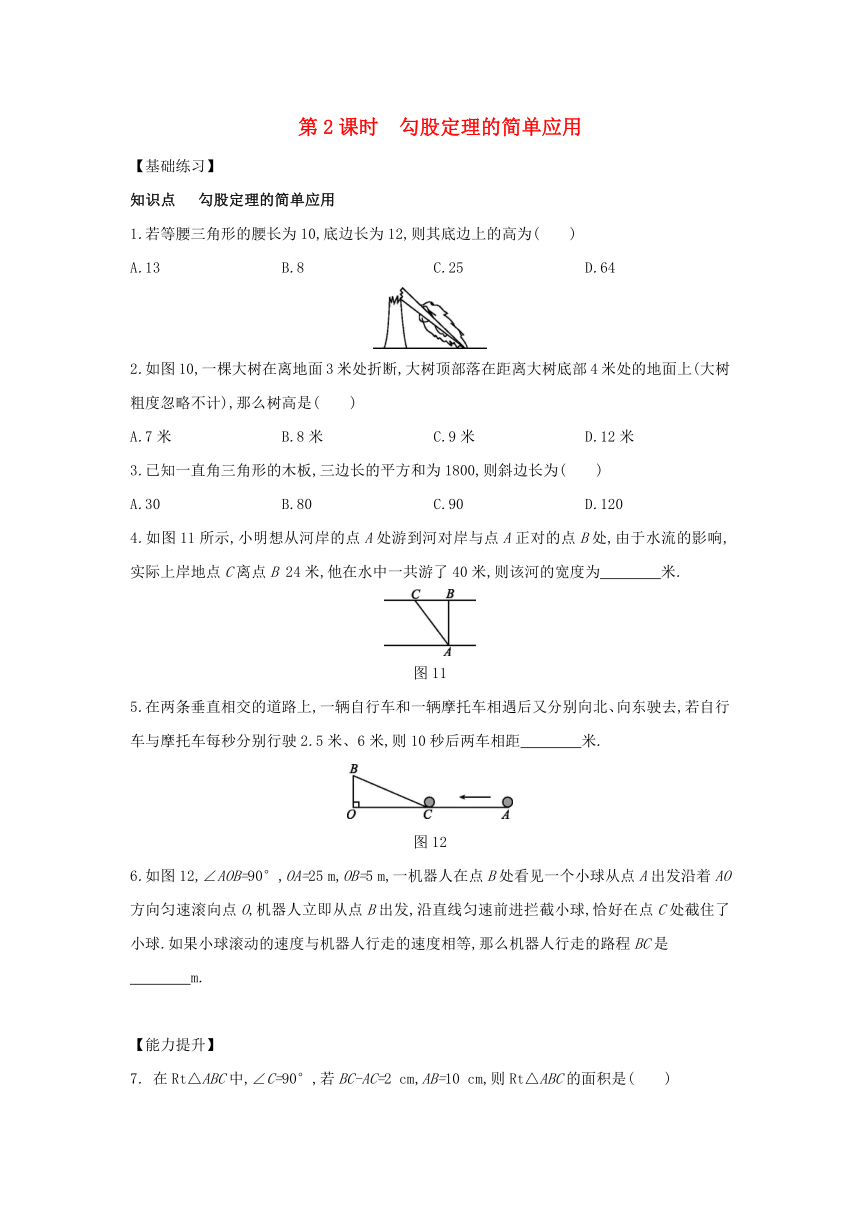
第2课时 勾股定理的简单应用
【基础练习】
知识点 勾股定理的简单应用
1.若等腰三角形的腰长为10,底边长为12,则其底边上的高为( )
A.13 B.8 C.25 D.64
2.如图10,一棵大树在离地面3米处折断,大树顶部落在距离大树底部4米处的地面上(大树粗度忽略不计),那么树高是( )
A.7米 B.8米 C.9米 D.12米
3.已知一直角三角形的木板,三边长的平方和为1800,则斜边长为( )
A.30 B.80 C.90 D.120
4.如图11所示,小明想从河岸的点A处游到河对岸与点A正对的点B处,由于水流的影响,实际上岸地点C离点B 24米,他在水中一共游了40米,则该河的宽度为 米.
图11
5.在两条垂直相交的道路上,一辆自行车和一辆摩托车相遇后又分别向北、向东驶去,若自行车与摩托车每秒分别行驶2.5米、6米,则10秒后两车相距 米.?
图12
6.如图12,∠AOB=90°,OA=25 m,OB=5 m,一机器人在点B处看见一个小球从点A出发沿着AO方向匀速滚向点O,机器人立即从点B出发,沿直线匀速前进拦截小球,恰好在点C处截住了小球.如果小球滚动的速度与机器人行走的速度相等,那么机器人行走的路程BC是
m.?
【能力提升】
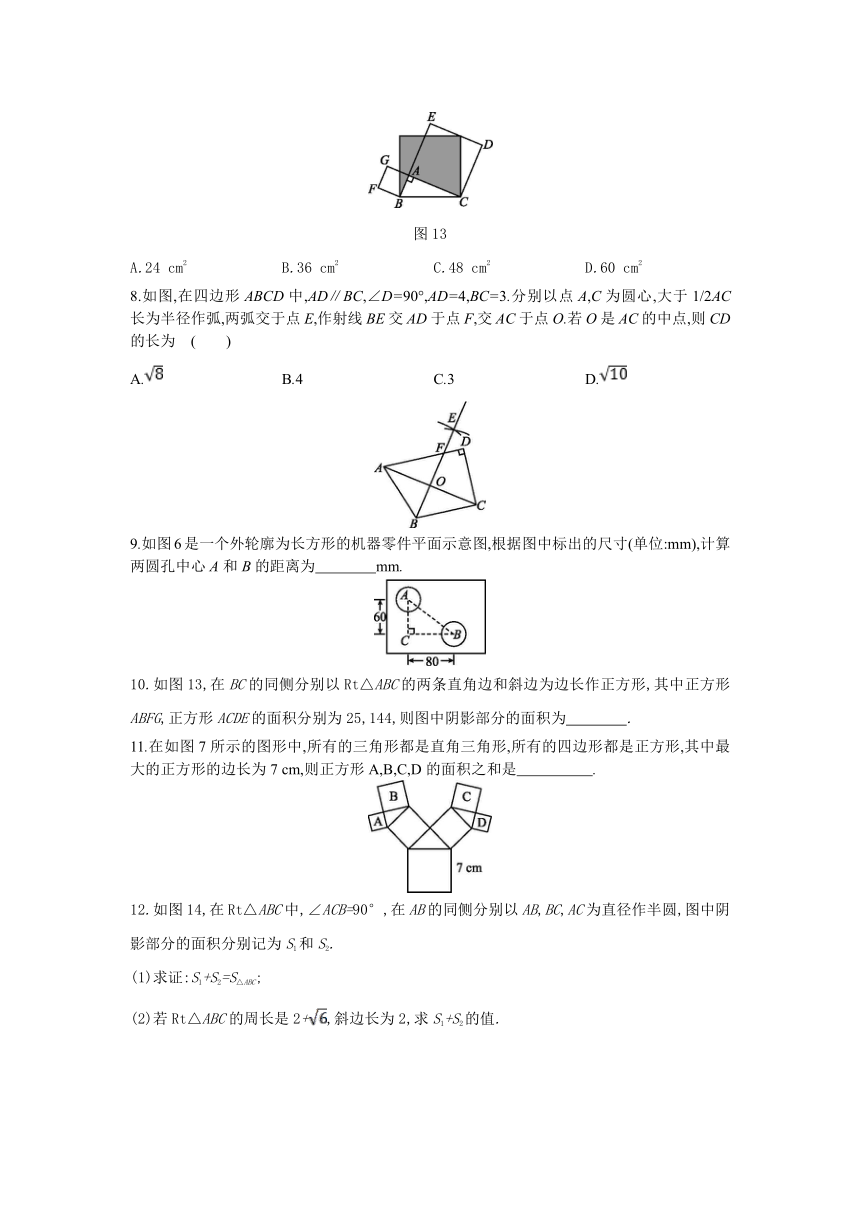
7. 在Rt△ABC中,∠C=90°,若BC-AC=2 cm,AB=10 cm,则Rt△ABC的面积是( )
图13
A.24 cm2 B.36 cm2 C.48 cm2 D.60 cm2
8.如图,在四边形ABCD中,AD∥BC,∠D=90°,AD=4,BC=3.分别以点A,C为圆心,大于1/2AC长为半径作弧,两弧交于点E,作射线BE交AD于点F,交AC于点O.若O是AC的中点,则CD的长为 ( )
A. B.4 C.3 D.
9.如图6是一个外轮廓为长方形的机器零件平面示意图,根据图中标出的尺寸(单位:mm),计算两圆孔中心A和B的距离为 mm.?
10.如图13,在BC的同侧分别以Rt△ABC的两条直角边和斜边为边长作正方形,其中正方形ABFG,正方形ACDE的面积分别为25,144,则图中阴影部分的面积为 .?
11.在如图7所示的图形中,所有的三角形都是直角三角形,所有的四边形都是正方形,其中最大的正方形的边长为7 cm,则正方形A,B,C,D的面积之和是 .?
12.如图14,在Rt△ABC中,∠ACB=90°,在AB的同侧分别以AB,BC,AC为直径作半圆,图中阴影部分的面积分别记为S1和S2.
(1)求证:S1+S2=S△ABC;
(2)若Rt△ABC的周长是2+,斜边长为2,求S1+S2的值.
图14
13.如图15,正方形网格中每个小正方形的边长都是1,每个小正方形的顶点叫做格点,以格点为顶点分别按下列要求画三角形.
(1)在图①中,画一个三角形,使它的三边长都是有理数;
(2)在图②中,画一个直角三角形,使它的三边长都是无理数;
(3)在图③中,画一个正方形,使它的面积是10.
图15
答案
1.B [解析] 作底边上的高并设此高的长度为x.根据勾股定理,得62+x2=102,解得x=8(负值已舍去).
故选B.
2.B [解析] 根据勾股定理可知大树折断部分的高度==5(米),则这棵大树折断前的高度=3+5=8(米).故选B.
3.A [解析] 设直角三角形的斜边长为x.
∵三边长的平方和为1800,
∴x2=900,解得x=30(负值已舍去).
故选A.
4.32 [解析] 根据题意,得∠ABC=90°,线段AB的长即为河宽.在Rt△ABC中,根据勾股定理,得AB===32(米).
故该河的宽度为32米.
5.65 [解析] 如图所示:
由题意可得,在Rt△ACB中,∠C=90°,AC=2.5×10=25(米),BC=6×10=60(米),则AB===65(米),则10秒后两车相距65米.故答案为65.
6.13 [解析] 设BC=x m,根据题意用x表示出AC和OC的长,根据勾股定理列出方程,解方程即可.
设BC=x m,则AC=x m,OC=(25-x)m.
由勾股定理,得BC2=OB2+OC2,
即x2=52+(25-x)2,解得x=13.
故机器人行走的路程BC是13 m.
7.A [解析] ∵∠C=90°,
∴AC2+BC2=AB2=100.
∵BC-AC=2,
∴(BC-AC)2=4,
即AC2+BC2-2AC·BC=4,
∴2AC·BC=96,
∴AC·BC=24,
即Rt△ABC的面积是24 cm2.
故选A.
A
9.100
10.[答案] 49 cm2
11 139 [解析] 根据题意知,AB2=25,
AC2=144,
所以AB=5,AC=12,BC===13,
所以S阴影=BC2-AB·AC=132-×5×12=139.
12.解:(1)证明:在Rt△ABC中,有BC2+AC2=AB2,
∴S1+S2=π×AC2+π×BC2+S△ABC-π×AB2=π(AC2+BC2-AB2)+S△ABC=S△ABC.
(2)∵AB+AC+BC=2+,AB=2,
∴AC+BC=.
两边平方,得AC2+BC2+2AC·BC=6.
又∵AC2+BC2=AB2=4,
∴2AC·BC=2,即AC·BC=1,
∴S1+S2=S△ABC=AC·BC=.
13.解:(1)三边长分别为3,4,5,如图①(三角形的形状、大小相同,但位置可能不同).
(2)答案不唯一,三边长分别为,,,如图②.
(3)如图③(正方形的形状、大小相同,但位置可能不同).
【基础练习】
知识点 勾股定理的简单应用
1.若等腰三角形的腰长为10,底边长为12,则其底边上的高为( )
A.13 B.8 C.25 D.64
2.如图10,一棵大树在离地面3米处折断,大树顶部落在距离大树底部4米处的地面上(大树粗度忽略不计),那么树高是( )
A.7米 B.8米 C.9米 D.12米
3.已知一直角三角形的木板,三边长的平方和为1800,则斜边长为( )
A.30 B.80 C.90 D.120
4.如图11所示,小明想从河岸的点A处游到河对岸与点A正对的点B处,由于水流的影响,实际上岸地点C离点B 24米,他在水中一共游了40米,则该河的宽度为 米.
图11
5.在两条垂直相交的道路上,一辆自行车和一辆摩托车相遇后又分别向北、向东驶去,若自行车与摩托车每秒分别行驶2.5米、6米,则10秒后两车相距 米.?
图12
6.如图12,∠AOB=90°,OA=25 m,OB=5 m,一机器人在点B处看见一个小球从点A出发沿着AO方向匀速滚向点O,机器人立即从点B出发,沿直线匀速前进拦截小球,恰好在点C处截住了小球.如果小球滚动的速度与机器人行走的速度相等,那么机器人行走的路程BC是
m.?
【能力提升】
7. 在Rt△ABC中,∠C=90°,若BC-AC=2 cm,AB=10 cm,则Rt△ABC的面积是( )
图13
A.24 cm2 B.36 cm2 C.48 cm2 D.60 cm2
8.如图,在四边形ABCD中,AD∥BC,∠D=90°,AD=4,BC=3.分别以点A,C为圆心,大于1/2AC长为半径作弧,两弧交于点E,作射线BE交AD于点F,交AC于点O.若O是AC的中点,则CD的长为 ( )
A. B.4 C.3 D.
9.如图6是一个外轮廓为长方形的机器零件平面示意图,根据图中标出的尺寸(单位:mm),计算两圆孔中心A和B的距离为 mm.?
10.如图13,在BC的同侧分别以Rt△ABC的两条直角边和斜边为边长作正方形,其中正方形ABFG,正方形ACDE的面积分别为25,144,则图中阴影部分的面积为 .?
11.在如图7所示的图形中,所有的三角形都是直角三角形,所有的四边形都是正方形,其中最大的正方形的边长为7 cm,则正方形A,B,C,D的面积之和是 .?
12.如图14,在Rt△ABC中,∠ACB=90°,在AB的同侧分别以AB,BC,AC为直径作半圆,图中阴影部分的面积分别记为S1和S2.
(1)求证:S1+S2=S△ABC;
(2)若Rt△ABC的周长是2+,斜边长为2,求S1+S2的值.
图14
13.如图15,正方形网格中每个小正方形的边长都是1,每个小正方形的顶点叫做格点,以格点为顶点分别按下列要求画三角形.
(1)在图①中,画一个三角形,使它的三边长都是有理数;
(2)在图②中,画一个直角三角形,使它的三边长都是无理数;
(3)在图③中,画一个正方形,使它的面积是10.
图15
答案
1.B [解析] 作底边上的高并设此高的长度为x.根据勾股定理,得62+x2=102,解得x=8(负值已舍去).
故选B.
2.B [解析] 根据勾股定理可知大树折断部分的高度==5(米),则这棵大树折断前的高度=3+5=8(米).故选B.
3.A [解析] 设直角三角形的斜边长为x.
∵三边长的平方和为1800,
∴x2=900,解得x=30(负值已舍去).
故选A.
4.32 [解析] 根据题意,得∠ABC=90°,线段AB的长即为河宽.在Rt△ABC中,根据勾股定理,得AB===32(米).
故该河的宽度为32米.
5.65 [解析] 如图所示:
由题意可得,在Rt△ACB中,∠C=90°,AC=2.5×10=25(米),BC=6×10=60(米),则AB===65(米),则10秒后两车相距65米.故答案为65.
6.13 [解析] 设BC=x m,根据题意用x表示出AC和OC的长,根据勾股定理列出方程,解方程即可.
设BC=x m,则AC=x m,OC=(25-x)m.
由勾股定理,得BC2=OB2+OC2,
即x2=52+(25-x)2,解得x=13.
故机器人行走的路程BC是13 m.
7.A [解析] ∵∠C=90°,
∴AC2+BC2=AB2=100.
∵BC-AC=2,
∴(BC-AC)2=4,
即AC2+BC2-2AC·BC=4,
∴2AC·BC=96,
∴AC·BC=24,
即Rt△ABC的面积是24 cm2.
故选A.
A
9.100
10.[答案] 49 cm2
11 139 [解析] 根据题意知,AB2=25,
AC2=144,
所以AB=5,AC=12,BC===13,
所以S阴影=BC2-AB·AC=132-×5×12=139.
12.解:(1)证明:在Rt△ABC中,有BC2+AC2=AB2,
∴S1+S2=π×AC2+π×BC2+S△ABC-π×AB2=π(AC2+BC2-AB2)+S△ABC=S△ABC.
(2)∵AB+AC+BC=2+,AB=2,
∴AC+BC=.
两边平方,得AC2+BC2+2AC·BC=6.
又∵AC2+BC2=AB2=4,
∴2AC·BC=2,即AC·BC=1,
∴S1+S2=S△ABC=AC·BC=.
13.解:(1)三边长分别为3,4,5,如图①(三角形的形状、大小相同,但位置可能不同).
(2)答案不唯一,三边长分别为,,,如图②.
(3)如图③(正方形的形状、大小相同,但位置可能不同).
