2021_2022学年八年级数学上册第14章勾股定理14.1.1第1课时勾股定理及其证明练习题新版华东师大版
文档属性
| 名称 | 2021_2022学年八年级数学上册第14章勾股定理14.1.1第1课时勾股定理及其证明练习题新版华东师大版 |

|
|
| 格式 | doc | ||
| 文件大小 | 531.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-07 00:00:00 | ||
图片预览

文档简介
第1课时 勾股定理及其证明
【基础练习】
知识点 1 勾股定理
1.下列说法中正确的是( )
A.已知a,b,c分别是直角三角形的三边长,则必有a2+b2=c2
B.直角三角形中,两条边的平方和等于第三边的平方
C.在Rt△ABC中,若∠B=90°,边BC,CA,AB的长分别是a,b,c,则c2=a2+b2
D.在Rt△ABC中,若∠A=90°,a,b,c分别是∠A,∠B,∠C的对边,则b2+c2=a2
2.在Rt△ABC中,BC=1,AC=2,∠B=90°,则AB的长是( )
A. B.2 C.1 D.
3.如图1,在正方形网格中,线段AB=,CD=,那么线段EF的长度为( )
A. B. C. D.
图1
4.如图2,长方形OABC的边OA的长为2,边AB的长为1,OA在数轴上,以原点O为圆心,对角线OB的长为半径画弧,交数轴上原点的右侧于一点,则这个点表示的实数是 .?
图2
5.在△ABC中,∠C=90°,BC=a,AC=b,AB=c.
(1)若a=6,b=8,求c;
(2)若c=61,a=60,求b;
(3)若a∶b=3∶4,c=25,求b.
知识点 2 勾股定理的证明
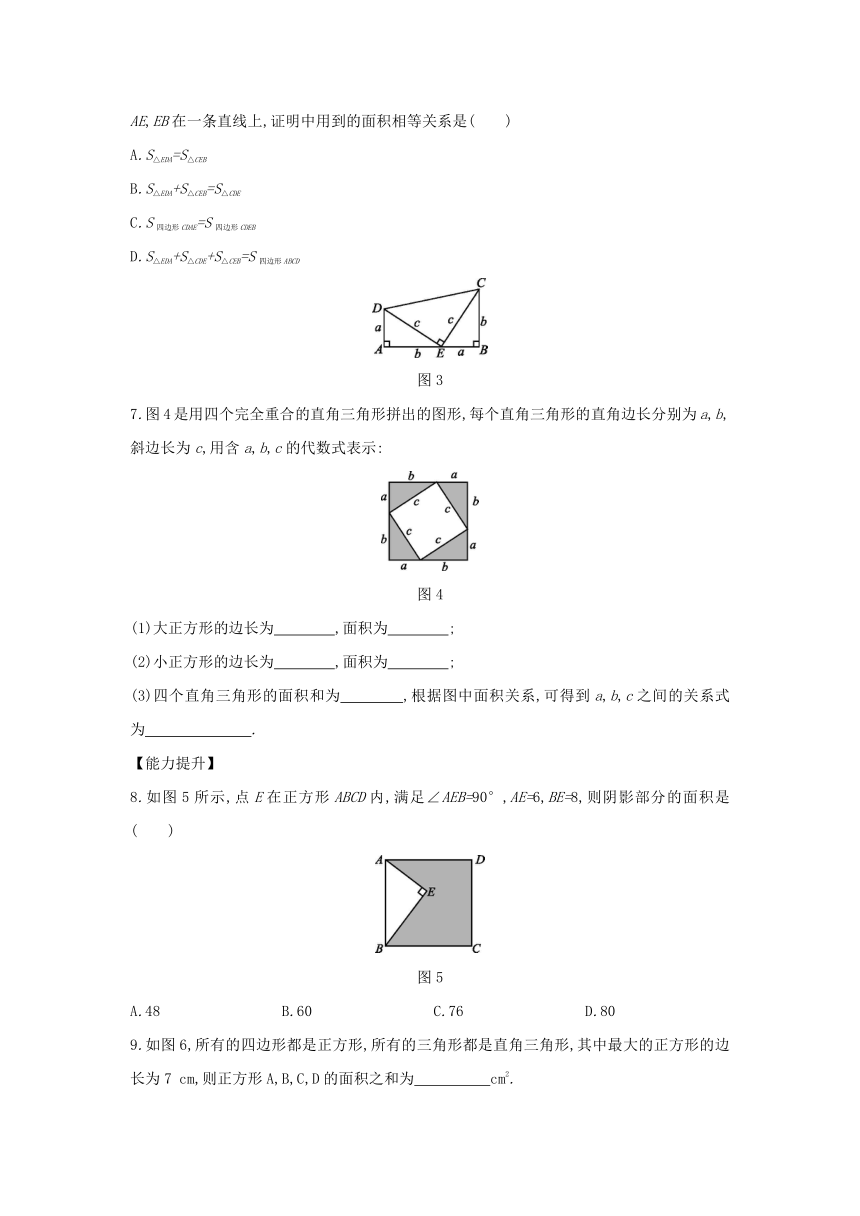
6.历史上对勾股定理的一种证法采用了如图3所示的图形,其中两个全等的直角三角形的边AE,EB在一条直线上,证明中用到的面积相等关系是( )
A.S△EDA=S△CEB
B.S△EDA+S△CEB=S△CDE
C.S四边形CDAE=S四边形CDEB
D.S△EDA+S△CDE+S△CEB=S四边形ABCD
图3
7.图4是用四个完全重合的直角三角形拼出的图形,每个直角三角形的直角边长分别为a,b,斜边长为c,用含a,b,c的代数式表示:
图4
(1)大正方形的边长为 ,面积为 ;?
(2)小正方形的边长为 ,面积为 ;?
(3)四个直角三角形的面积和为 ,根据图中面积关系,可得到a,b,c之间的关系式为 .?
【能力提升】
8.如图5所示,点E在正方形ABCD内,满足∠AEB=90°,AE=6,BE=8,则阴影部分的面积是( )
图5
A.48 B.60 C.76 D.80
9.如图6,所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大的正方形的边长为7 cm,则正方形A,B,C,D的面积之和为 cm2.
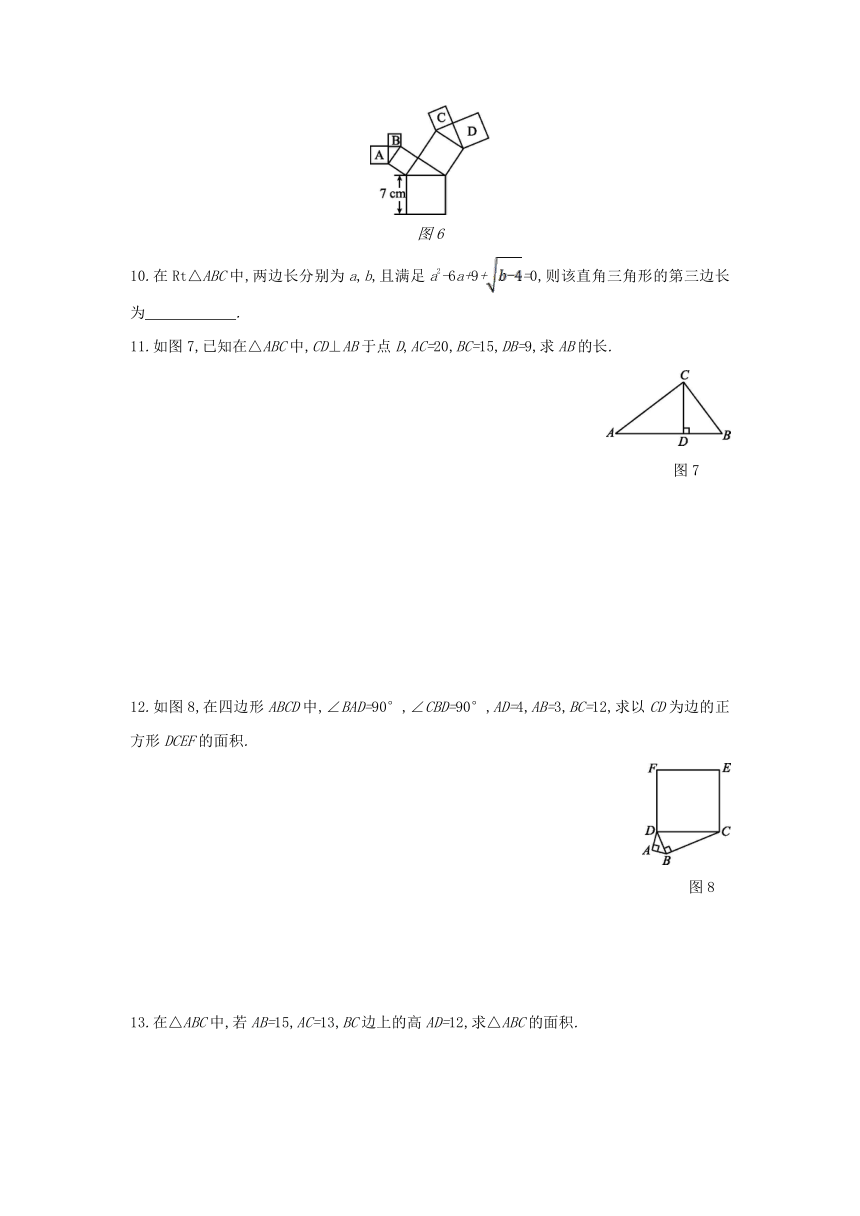
图6
10.在Rt△ABC中,两边长分别为a,b,且满足a2-6a+9+=0,则该直角三角形的第三边长为 .?
11.如图7,已知在△ABC中,CD⊥AB于点D,AC=20,BC=15,DB=9,求AB的长.
图7
12.如图8,在四边形ABCD中,∠BAD=90°,∠CBD=90°,AD=4,AB=3,BC=12,求以CD为边的正方形DCEF的面积.
图8
13.在△ABC中,若AB=15,AC=13,BC边上的高AD=12,求△ABC的面积.
14.[问题情境]
勾股定理是一个古老的数学定理,它有多种证明方法,三国时期的数学家赵爽根据弦图,利用面积法进行了证明.著名数学家华罗庚曾提出把“数形关系”(勾股定理)带到其他星球,作为地球人与其他星球“人”进行第一次“谈话”的语言.
[定理表述]
请你根据图9①中的直角三角形叙述勾股定理(用文字及符号语言叙述);
图9
[尝试证明]
以图①中的直角三角形为基础,可以拼成如图②所示的图形,请你利用图②,验证勾股定理;
[知识拓展]
利用图②中的图形,我们可以证明<,其证明步骤如下:
∵BC=a+b,AD= ,?
且在四边形ABCD中,有BC AD(填大小关系),即 ,?
∴<.
答案
1.D [解析] A没有明确c是斜边长,所以A是错误的;B显然是错误的;C由于条件中明确了∠B=90°,所以说CA是斜边,即b是斜边长,根据勾股定理应有b2=a2+c2,所以C是错误的;D由于条件中明确了∠A=90°,所以a为斜边长,所以D是正确的.故选D.
2.D [解析] ∵在Rt△ABC中,BC=1,AC=2,∠B=90°,∴AB====.
故选D.
3.D [解析] ∵AB==,CD==,∴图形中的网格是由边长为1的小正方形构成的,则EF==.故选D.
4. [解析] 由勾股定理可知OB===.
5.解:(1)在△ABC中,∠C=90°,a=6,b=8,
∴c===10.
(2)∵在△ABC中,∠C=90°,c=61,a=60,
∴b===11.
(3)∵a∶b=3∶4,
∴可设a=3k,则b=4k.
在△ABC中,∠C=90°,c=25,
∴a2+b2=c2,即(3k)2+(4k)2=252,
∴k=5(负值不合题意,已舍去),
∴b=20.
6.D [解析] 由S△EDA+S△CDE+S△CEB=S四边形ABCD,可得ab+c2+ab=(a+b)2,
∴c2+2ab=a2+2ab+b2,
整理,得a2+b2=c2,
∴证明中用到的面积相等关系是S△EDA+S△CDE+S△CEB=S四边形ABCD.
故选D.
7.(1)a+b (a+b)2 (2)c c2
(3)2ab a2+b2=c2
8.C
9.49 [解析] 根据正方形面积公式和勾股定理,可以得到正方形A,B,C,D的面积之和正好等于边长为7 cm的正方形的面积,即49 cm2.故答案为49.
10.5或 [解析] ∵a2-6a+9+=0,
∴(a-3)2+=0,
∴a-3=0,b-4=0,
解得a=3,b=4.
当4是直角边长时,第三边长==5;
当4是斜边长时,第三边长==.
故答案为5或.
11.解:∵CD⊥AB,AC=20,BC=15,DB=9,
∴在Rt△BCD中,CD2=BC2-DB2=152-92=144,
∴在Rt△ACD中,AD2=AC2-CD2=202-144=256,
∴AD=16,
∴AB=AD+DB=16+9=25.
12.[解析] 根据勾股定理分别求出BD,CD,根据正方形的面积公式计算即可.
解:∵∠BAD=90°,
∴AD2+AB2=BD2,
即42+32=BD2,∴BD=5.
∵∠CBD=90°,
∴BD2+BC2=CD2,
即52+122=CD2,∴CD=13,
∴S正方形DCEF=132=169.
13.[解析] 当已知三角形的两边和第三条边上的高时,三角形是不唯一的,要考虑第三条边上的高是在三角形的内部还是在三角形的外部,稍不注意就容易漏掉一解而导致错误.
解:在Rt△ABD中,由勾股定理,得
BD===9.
在Rt△ADC中,由勾股定理,得
CD===5.
如图,若△ABC是锐角三角形ABC1,
则BC1=BD+C1D=9+5=14,
所以=BC1·AD=×14×12=84;
若△ABC是钝角三角形ABC2,
则BC2=BD-C2D=9-5=4,
所以=BC2·AD=×4×12=24.
综上可得,△ABC的面积是84或24.
14.解:[定理表述]
直角三角形两直角边的平方和等于斜边的平方.即如果直角三角形的两直角边长分别为a,b,斜边长为c,那么a2+b2=c2.
[尝试证明]
∵Rt△ABE≌Rt△ECD,∴∠AEB=∠EDC.
又∵∠EDC+∠DEC=90°,
∴∠AEB+∠DEC=90°,∴∠AED=90°.
∵S四边形ABCD=SRt△ABE+SRt△ECD+SRt△AED,
∴(a+b)(a+b)=ab+ab+c2,
整理,得a2+b2=c2.
[知识拓展]
c < a+b
【基础练习】
知识点 1 勾股定理
1.下列说法中正确的是( )
A.已知a,b,c分别是直角三角形的三边长,则必有a2+b2=c2
B.直角三角形中,两条边的平方和等于第三边的平方
C.在Rt△ABC中,若∠B=90°,边BC,CA,AB的长分别是a,b,c,则c2=a2+b2
D.在Rt△ABC中,若∠A=90°,a,b,c分别是∠A,∠B,∠C的对边,则b2+c2=a2
2.在Rt△ABC中,BC=1,AC=2,∠B=90°,则AB的长是( )
A. B.2 C.1 D.
3.如图1,在正方形网格中,线段AB=,CD=,那么线段EF的长度为( )
A. B. C. D.
图1
4.如图2,长方形OABC的边OA的长为2,边AB的长为1,OA在数轴上,以原点O为圆心,对角线OB的长为半径画弧,交数轴上原点的右侧于一点,则这个点表示的实数是 .?
图2
5.在△ABC中,∠C=90°,BC=a,AC=b,AB=c.
(1)若a=6,b=8,求c;
(2)若c=61,a=60,求b;
(3)若a∶b=3∶4,c=25,求b.
知识点 2 勾股定理的证明
6.历史上对勾股定理的一种证法采用了如图3所示的图形,其中两个全等的直角三角形的边AE,EB在一条直线上,证明中用到的面积相等关系是( )
A.S△EDA=S△CEB
B.S△EDA+S△CEB=S△CDE
C.S四边形CDAE=S四边形CDEB
D.S△EDA+S△CDE+S△CEB=S四边形ABCD
图3
7.图4是用四个完全重合的直角三角形拼出的图形,每个直角三角形的直角边长分别为a,b,斜边长为c,用含a,b,c的代数式表示:
图4
(1)大正方形的边长为 ,面积为 ;?
(2)小正方形的边长为 ,面积为 ;?
(3)四个直角三角形的面积和为 ,根据图中面积关系,可得到a,b,c之间的关系式为 .?
【能力提升】
8.如图5所示,点E在正方形ABCD内,满足∠AEB=90°,AE=6,BE=8,则阴影部分的面积是( )
图5
A.48 B.60 C.76 D.80
9.如图6,所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大的正方形的边长为7 cm,则正方形A,B,C,D的面积之和为 cm2.
图6
10.在Rt△ABC中,两边长分别为a,b,且满足a2-6a+9+=0,则该直角三角形的第三边长为 .?
11.如图7,已知在△ABC中,CD⊥AB于点D,AC=20,BC=15,DB=9,求AB的长.
图7
12.如图8,在四边形ABCD中,∠BAD=90°,∠CBD=90°,AD=4,AB=3,BC=12,求以CD为边的正方形DCEF的面积.
图8
13.在△ABC中,若AB=15,AC=13,BC边上的高AD=12,求△ABC的面积.
14.[问题情境]
勾股定理是一个古老的数学定理,它有多种证明方法,三国时期的数学家赵爽根据弦图,利用面积法进行了证明.著名数学家华罗庚曾提出把“数形关系”(勾股定理)带到其他星球,作为地球人与其他星球“人”进行第一次“谈话”的语言.
[定理表述]
请你根据图9①中的直角三角形叙述勾股定理(用文字及符号语言叙述);
图9
[尝试证明]
以图①中的直角三角形为基础,可以拼成如图②所示的图形,请你利用图②,验证勾股定理;
[知识拓展]
利用图②中的图形,我们可以证明<,其证明步骤如下:
∵BC=a+b,AD= ,?
且在四边形ABCD中,有BC AD(填大小关系),即 ,?
∴<.
答案
1.D [解析] A没有明确c是斜边长,所以A是错误的;B显然是错误的;C由于条件中明确了∠B=90°,所以说CA是斜边,即b是斜边长,根据勾股定理应有b2=a2+c2,所以C是错误的;D由于条件中明确了∠A=90°,所以a为斜边长,所以D是正确的.故选D.
2.D [解析] ∵在Rt△ABC中,BC=1,AC=2,∠B=90°,∴AB====.
故选D.
3.D [解析] ∵AB==,CD==,∴图形中的网格是由边长为1的小正方形构成的,则EF==.故选D.
4. [解析] 由勾股定理可知OB===.
5.解:(1)在△ABC中,∠C=90°,a=6,b=8,
∴c===10.
(2)∵在△ABC中,∠C=90°,c=61,a=60,
∴b===11.
(3)∵a∶b=3∶4,
∴可设a=3k,则b=4k.
在△ABC中,∠C=90°,c=25,
∴a2+b2=c2,即(3k)2+(4k)2=252,
∴k=5(负值不合题意,已舍去),
∴b=20.
6.D [解析] 由S△EDA+S△CDE+S△CEB=S四边形ABCD,可得ab+c2+ab=(a+b)2,
∴c2+2ab=a2+2ab+b2,
整理,得a2+b2=c2,
∴证明中用到的面积相等关系是S△EDA+S△CDE+S△CEB=S四边形ABCD.
故选D.
7.(1)a+b (a+b)2 (2)c c2
(3)2ab a2+b2=c2
8.C
9.49 [解析] 根据正方形面积公式和勾股定理,可以得到正方形A,B,C,D的面积之和正好等于边长为7 cm的正方形的面积,即49 cm2.故答案为49.
10.5或 [解析] ∵a2-6a+9+=0,
∴(a-3)2+=0,
∴a-3=0,b-4=0,
解得a=3,b=4.
当4是直角边长时,第三边长==5;
当4是斜边长时,第三边长==.
故答案为5或.
11.解:∵CD⊥AB,AC=20,BC=15,DB=9,
∴在Rt△BCD中,CD2=BC2-DB2=152-92=144,
∴在Rt△ACD中,AD2=AC2-CD2=202-144=256,
∴AD=16,
∴AB=AD+DB=16+9=25.
12.[解析] 根据勾股定理分别求出BD,CD,根据正方形的面积公式计算即可.
解:∵∠BAD=90°,
∴AD2+AB2=BD2,
即42+32=BD2,∴BD=5.
∵∠CBD=90°,
∴BD2+BC2=CD2,
即52+122=CD2,∴CD=13,
∴S正方形DCEF=132=169.
13.[解析] 当已知三角形的两边和第三条边上的高时,三角形是不唯一的,要考虑第三条边上的高是在三角形的内部还是在三角形的外部,稍不注意就容易漏掉一解而导致错误.
解:在Rt△ABD中,由勾股定理,得
BD===9.
在Rt△ADC中,由勾股定理,得
CD===5.
如图,若△ABC是锐角三角形ABC1,
则BC1=BD+C1D=9+5=14,
所以=BC1·AD=×14×12=84;
若△ABC是钝角三角形ABC2,
则BC2=BD-C2D=9-5=4,
所以=BC2·AD=×4×12=24.
综上可得,△ABC的面积是84或24.
14.解:[定理表述]
直角三角形两直角边的平方和等于斜边的平方.即如果直角三角形的两直角边长分别为a,b,斜边长为c,那么a2+b2=c2.
[尝试证明]
∵Rt△ABE≌Rt△ECD,∴∠AEB=∠EDC.
又∵∠EDC+∠DEC=90°,
∴∠AEB+∠DEC=90°,∴∠AED=90°.
∵S四边形ABCD=SRt△ABE+SRt△ECD+SRt△AED,
∴(a+b)(a+b)=ab+ab+c2,
整理,得a2+b2=c2.
[知识拓展]
c < a+b
