2021_2022学年八年级数学上册第13章全等三角形13.26斜边直角边同步练习新版华东师大版
文档属性
| 名称 | 2021_2022学年八年级数学上册第13章全等三角形13.26斜边直角边同步练习新版华东师大版 |

|
|
| 格式 | docx | ||
| 文件大小 | 154.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-07 00:00:00 | ||
图片预览

文档简介
13.2 6.斜边直角边
一、选择题
1.由下列条件不能判定两个直角三角形全等的是 ( )
A.两条直角边分别相等
B.斜边和一个锐角分别相等
C.两个锐角分别相等
D.斜边和一条直角边分别相等
2.如图1,AC=BC,CA⊥OA,CB⊥OB,垂足分别为A,B,则Rt△AOC≌Rt△BOC的理由是 ( )
A.S.S.S. B.A.S.A. C.S.A.S. D.H.L.
图1
3.如图2,BE=CF,AE⊥BC于点E,DF⊥BC于点F,要根据“H.L.”证明Rt△ABE≌Rt△DCF,则还要添加一个条件是 ( )
图2
A.AB=DC B.∠A=∠D
C.∠B=∠C D.AE=DF
4.如图3,已知E为AC上一点,BC⊥CA,ED⊥AB,垂足分别为C,D,BD=BC,AE=8 cm,DE=6 cm,则AC等于 ( )
图3
A.10 cm B.12 cm C.14 cm D.16 cm
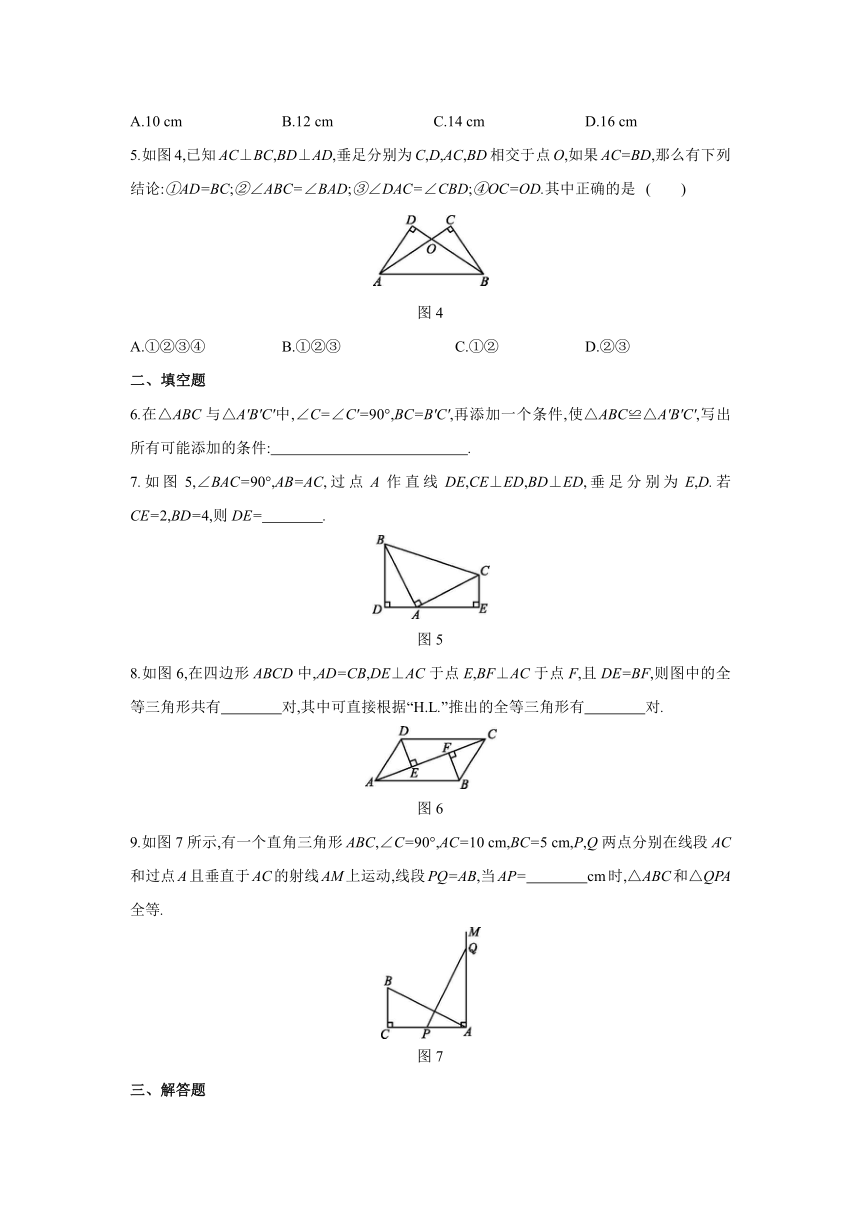
5.如图4,已知AC⊥BC,BD⊥AD,垂足分别为C,D,AC,BD相交于点O,如果AC=BD,那么有下列结论:①AD=BC;②∠ABC=∠BAD;③∠DAC=∠CBD;④OC=OD.其中正确的是 ( )
图4
A.①②③④ B.①②③ C.①② D.②③
二、填空题
6.在△ABC与△A'B'C'中,∠C=∠C'=90°,BC=B'C',再添加一个条件,使△ABC≌△A'B'C',写出所有可能添加的条件: .?
7.如图5,∠BAC=90°,AB=AC,过点A作直线DE,CE⊥ED,BD⊥ED,垂足分别为E,D.若CE=2,BD=4,则DE= .?
图5
8.如图6,在四边形ABCD中,AD=CB,DE⊥AC于点E,BF⊥AC于点F,且DE=BF,则图中的全等三角形共有 对,其中可直接根据“H.L.”推出的全等三角形有 对.?
图6
9.如图7所示,有一个直角三角形ABC,∠C=90°,AC=10 cm,BC=5 cm,P,Q两点分别在线段AC和过点A且垂直于AC的射线AM上运动,线段PQ=AB,当AP= cm时,△ABC和△QPA全等.?
图7
三、解答题
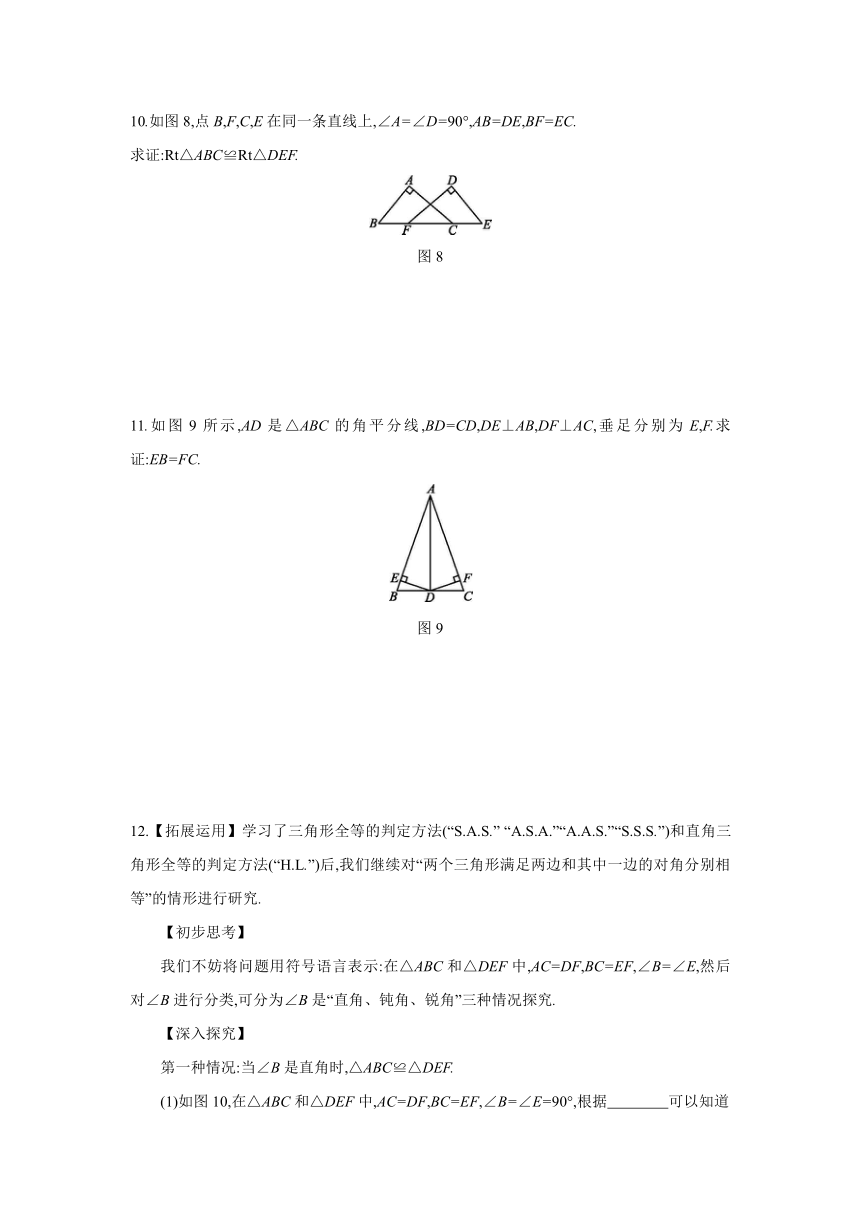
10.如图8,点B,F,C,E在同一条直线上,∠A=∠D=90°,AB=DE,BF=EC.
求证:Rt△ABC≌Rt△DEF.
图8
11.如图9所示,AD是△ABC的角平分线,BD=CD,DE⊥AB,DF⊥AC,垂足分别为E,F.求证:EB=FC.
图9
12.【拓展运用】学习了三角形全等的判定方法(“S.A.S.” “A.S.A.”“A.A.S.”“S.S.S.”)和直角三角形全等的判定方法(“H.L.”)后,我们继续对“两个三角形满足两边和其中一边的对角分别相等”的情形进行研究.
【初步思考】
我们不妨将问题用符号语言表示:在△ABC和△DEF中,AC=DF,BC=EF,∠B=∠E,然后对∠B进行分类,可分为∠B是“直角、钝角、锐角”三种情况探究.
【深入探究】
第一种情况:当∠B是直角时,△ABC≌△DEF.
(1)如图10,在△ABC和△DEF中,AC=DF,BC=EF,∠B=∠E=90°,根据 可以知道Rt△ABC≌Rt△DEF.?
图10
第二种情况,当∠B是钝角时,△ABC≌△DEF.
(2)如图11,在△ABC和△DEF中,AC=DF,BC=EF,∠B=∠E,且∠B,∠E都是钝角.
求证:△ABC≌△DEF.
图11
第三种情况:当∠B是锐角时,△ABC和△DEF不一定全等.
(3)在△ABC和△DEF中,AC=DF,BC=EF,∠B=∠E,且∠B,∠E都是锐角,请你在图12中作出△DEF,使△DEF和△ABC不全等.(不写作法,保留作图痕迹)
图12
(4)∠B还满足什么条件,就可以使△ABC≌△DEF?请你写出结论:在△ABC和△DEF中,AC=DF,BC=EF,∠B=∠E,且∠B,∠E都是锐角.若 ,则△ABC≌△DEF.?
答案
1.C
2.[解析] D ∵CA⊥OA,CB⊥OB,∴∠A=∠B=90°.
在Rt△AOC和Rt△BOC中,∵AC=BC,CO=CO,∴Rt△AOC≌Rt△BOC(H.L.).故选D.
3.[解析] A 添加条件AB=DC,理由:∵AE⊥BC,DF⊥BC,∴∠CFD=∠BEA=90°.在Rt△ABE和Rt△DCF中,∵AB=DC,BE=CF,∴Rt△ABE≌Rt△DCF(H.L.).故选A.
4.[解析] C ∵BC⊥CA,ED⊥AB,∴∠BDE=∠BCE=90°.在Rt△DEB和Rt△CEB中,
∵BE=BE,BD=BC,∴Rt△DEB≌Rt△CEB,∴DE=CE,∴AC=AE+CE=AE+DE=8+6=14(cm).
5.[解析] A 由AC=BD,AB=BA,得Rt△ADB≌Rt△BCA(H.L.),
故AD=BC,∠ABC=∠BAD,∠CAB=∠DBA,进而得∠DAC=∠CBD和△ADO≌△BCO,
所以OC=OD.综上可知,正确的是①②③④.故选A.
6.AC=A'C',∠B=∠B',∠A=∠A',AB=A'B'
7.6 8.3 1 9.5或10
10.证明:∵BF=EC,∴BF+FC=EC+FC,
即BC=EF.
∵∠A=∠D=90°,
∴△ABC和△DEF都是直角三角形.
在Rt△ABC和Rt△DEF中,
∵AB=DE,BC=EF,
∴Rt△ABC≌Rt△DEF(H.L.).
11.证明:因为AD是△ABC的角平分线,
所以∠DAE=∠DAF.
因为DE⊥AB,DF⊥AC,
所以∠AED=∠AFD=90°.
在△AED和△AFD中,因为∠DAE=∠DAF,∠AED=∠AFD,AD=AD,
所以△AED≌△AFD(A.A.S.),
所以DE=DF.
在Rt△DEB和Rt△DFC中,
因为BD=CD,DE=DF,
所以Rt△DEB≌Rt△DFC(H.L.),
所以EB=FC.
12.解:(1)H.L.
(2)证明:如图①,过点C作CG⊥AB,交AB的延长线于点G,过点F作FH⊥DE,交DE的延长线于点H.
∵CG⊥AB,FH⊥DE,∴∠G=∠H=90°.
∵∠ABC=∠DEF,且∠ABC,∠DEF都是钝角,
∴180°-∠ABC=180°-∠DEF,
即∠CBG=∠FEH.
在△CBG和△FEH中,
∵∠CBG=∠FEH,∠G=∠H=90°,BC=EF,
∴△CBG≌△FEH(A.A.S.),
∴CG=FH.
在Rt△ACG和Rt△DFH中,
∵AC=DF,CG=FH,
∴Rt△ACG≌Rt△DFH(H.L.),
∴∠A=∠D.
在△ABC和△DEF中,
∵∠A=∠D,∠ABC=∠DEF,AC=DF,
∴△ABC≌△DEF(A.A.S.).
(3)如图②所示,△DEF和△ABC不全等.
(4)∠B≥∠A
一、选择题
1.由下列条件不能判定两个直角三角形全等的是 ( )
A.两条直角边分别相等
B.斜边和一个锐角分别相等
C.两个锐角分别相等
D.斜边和一条直角边分别相等
2.如图1,AC=BC,CA⊥OA,CB⊥OB,垂足分别为A,B,则Rt△AOC≌Rt△BOC的理由是 ( )
A.S.S.S. B.A.S.A. C.S.A.S. D.H.L.
图1
3.如图2,BE=CF,AE⊥BC于点E,DF⊥BC于点F,要根据“H.L.”证明Rt△ABE≌Rt△DCF,则还要添加一个条件是 ( )
图2
A.AB=DC B.∠A=∠D
C.∠B=∠C D.AE=DF
4.如图3,已知E为AC上一点,BC⊥CA,ED⊥AB,垂足分别为C,D,BD=BC,AE=8 cm,DE=6 cm,则AC等于 ( )
图3
A.10 cm B.12 cm C.14 cm D.16 cm
5.如图4,已知AC⊥BC,BD⊥AD,垂足分别为C,D,AC,BD相交于点O,如果AC=BD,那么有下列结论:①AD=BC;②∠ABC=∠BAD;③∠DAC=∠CBD;④OC=OD.其中正确的是 ( )
图4
A.①②③④ B.①②③ C.①② D.②③
二、填空题
6.在△ABC与△A'B'C'中,∠C=∠C'=90°,BC=B'C',再添加一个条件,使△ABC≌△A'B'C',写出所有可能添加的条件: .?
7.如图5,∠BAC=90°,AB=AC,过点A作直线DE,CE⊥ED,BD⊥ED,垂足分别为E,D.若CE=2,BD=4,则DE= .?
图5
8.如图6,在四边形ABCD中,AD=CB,DE⊥AC于点E,BF⊥AC于点F,且DE=BF,则图中的全等三角形共有 对,其中可直接根据“H.L.”推出的全等三角形有 对.?
图6
9.如图7所示,有一个直角三角形ABC,∠C=90°,AC=10 cm,BC=5 cm,P,Q两点分别在线段AC和过点A且垂直于AC的射线AM上运动,线段PQ=AB,当AP= cm时,△ABC和△QPA全等.?
图7
三、解答题
10.如图8,点B,F,C,E在同一条直线上,∠A=∠D=90°,AB=DE,BF=EC.
求证:Rt△ABC≌Rt△DEF.
图8
11.如图9所示,AD是△ABC的角平分线,BD=CD,DE⊥AB,DF⊥AC,垂足分别为E,F.求证:EB=FC.
图9
12.【拓展运用】学习了三角形全等的判定方法(“S.A.S.” “A.S.A.”“A.A.S.”“S.S.S.”)和直角三角形全等的判定方法(“H.L.”)后,我们继续对“两个三角形满足两边和其中一边的对角分别相等”的情形进行研究.
【初步思考】
我们不妨将问题用符号语言表示:在△ABC和△DEF中,AC=DF,BC=EF,∠B=∠E,然后对∠B进行分类,可分为∠B是“直角、钝角、锐角”三种情况探究.
【深入探究】
第一种情况:当∠B是直角时,△ABC≌△DEF.
(1)如图10,在△ABC和△DEF中,AC=DF,BC=EF,∠B=∠E=90°,根据 可以知道Rt△ABC≌Rt△DEF.?
图10
第二种情况,当∠B是钝角时,△ABC≌△DEF.
(2)如图11,在△ABC和△DEF中,AC=DF,BC=EF,∠B=∠E,且∠B,∠E都是钝角.
求证:△ABC≌△DEF.
图11
第三种情况:当∠B是锐角时,△ABC和△DEF不一定全等.
(3)在△ABC和△DEF中,AC=DF,BC=EF,∠B=∠E,且∠B,∠E都是锐角,请你在图12中作出△DEF,使△DEF和△ABC不全等.(不写作法,保留作图痕迹)
图12
(4)∠B还满足什么条件,就可以使△ABC≌△DEF?请你写出结论:在△ABC和△DEF中,AC=DF,BC=EF,∠B=∠E,且∠B,∠E都是锐角.若 ,则△ABC≌△DEF.?
答案
1.C
2.[解析] D ∵CA⊥OA,CB⊥OB,∴∠A=∠B=90°.
在Rt△AOC和Rt△BOC中,∵AC=BC,CO=CO,∴Rt△AOC≌Rt△BOC(H.L.).故选D.
3.[解析] A 添加条件AB=DC,理由:∵AE⊥BC,DF⊥BC,∴∠CFD=∠BEA=90°.在Rt△ABE和Rt△DCF中,∵AB=DC,BE=CF,∴Rt△ABE≌Rt△DCF(H.L.).故选A.
4.[解析] C ∵BC⊥CA,ED⊥AB,∴∠BDE=∠BCE=90°.在Rt△DEB和Rt△CEB中,
∵BE=BE,BD=BC,∴Rt△DEB≌Rt△CEB,∴DE=CE,∴AC=AE+CE=AE+DE=8+6=14(cm).
5.[解析] A 由AC=BD,AB=BA,得Rt△ADB≌Rt△BCA(H.L.),
故AD=BC,∠ABC=∠BAD,∠CAB=∠DBA,进而得∠DAC=∠CBD和△ADO≌△BCO,
所以OC=OD.综上可知,正确的是①②③④.故选A.
6.AC=A'C',∠B=∠B',∠A=∠A',AB=A'B'
7.6 8.3 1 9.5或10
10.证明:∵BF=EC,∴BF+FC=EC+FC,
即BC=EF.
∵∠A=∠D=90°,
∴△ABC和△DEF都是直角三角形.
在Rt△ABC和Rt△DEF中,
∵AB=DE,BC=EF,
∴Rt△ABC≌Rt△DEF(H.L.).
11.证明:因为AD是△ABC的角平分线,
所以∠DAE=∠DAF.
因为DE⊥AB,DF⊥AC,
所以∠AED=∠AFD=90°.
在△AED和△AFD中,因为∠DAE=∠DAF,∠AED=∠AFD,AD=AD,
所以△AED≌△AFD(A.A.S.),
所以DE=DF.
在Rt△DEB和Rt△DFC中,
因为BD=CD,DE=DF,
所以Rt△DEB≌Rt△DFC(H.L.),
所以EB=FC.
12.解:(1)H.L.
(2)证明:如图①,过点C作CG⊥AB,交AB的延长线于点G,过点F作FH⊥DE,交DE的延长线于点H.
∵CG⊥AB,FH⊥DE,∴∠G=∠H=90°.
∵∠ABC=∠DEF,且∠ABC,∠DEF都是钝角,
∴180°-∠ABC=180°-∠DEF,
即∠CBG=∠FEH.
在△CBG和△FEH中,
∵∠CBG=∠FEH,∠G=∠H=90°,BC=EF,
∴△CBG≌△FEH(A.A.S.),
∴CG=FH.
在Rt△ACG和Rt△DFH中,
∵AC=DF,CG=FH,
∴Rt△ACG≌Rt△DFH(H.L.),
∴∠A=∠D.
在△ABC和△DEF中,
∵∠A=∠D,∠ABC=∠DEF,AC=DF,
∴△ABC≌△DEF(A.A.S.).
(3)如图②所示,△DEF和△ABC不全等.
(4)∠B≥∠A
