2021_2022学年八年级数学上册第13章全等三角形13.31等腰三角形的性质同步练习新版华东师大版
文档属性
| 名称 | 2021_2022学年八年级数学上册第13章全等三角形13.31等腰三角形的性质同步练习新版华东师大版 |

|
|
| 格式 | docx | ||
| 文件大小 | 163.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-07 00:00:00 | ||
图片预览



文档简介
13.3
1.等腰三角形的性质
一、选择题
1.等腰三角形的对称轴是
( )
A.底边上的高所在的直线
B.底边上的高
C.底边上的中线
D.顶角平分线
2.如图1,在△ABC中,AB=AC,D是BC边的中点,则下列结论中不正确的是
( )
A.∠B=∠C
B.AD⊥BC
C.AD平分∠BAC
D.AB=2BD
图1
3.[2019·抚顺]
若一个等腰三角形的两边长分别为2,4,则第三边的长为
( )
A.2
B.3
C.4
D.2或4
4.若等腰三角形的一个内角为80°,则此三角形其余两个内角的度数分别为
( )
A.50°,50°
B.80°,20°
C.80°,50°
D.50°,50°或80°,20°
5.[2020·南充]
如图2,在等腰三角形ABC中,BD为∠ABC的平分线,∠A=36°,AB=AC=a,BC=b,则CD等于
( )
A.
B.
C.a-b
D.b-a
图2
6.如图3,在等边三角形ABC中,AD⊥BC于点D,E为AD上一点,∠CED=50°,则∠ABE等于
( )
A.10°
B.15°
C.20°
D.25°
图3
7.若等腰三角形一腰上的高与另一腰的夹角为30°,则这个等腰三角形顶角的度数为
( )
A.60°
B.120°
C.60°或150°
D.60°或120°
二、填空题
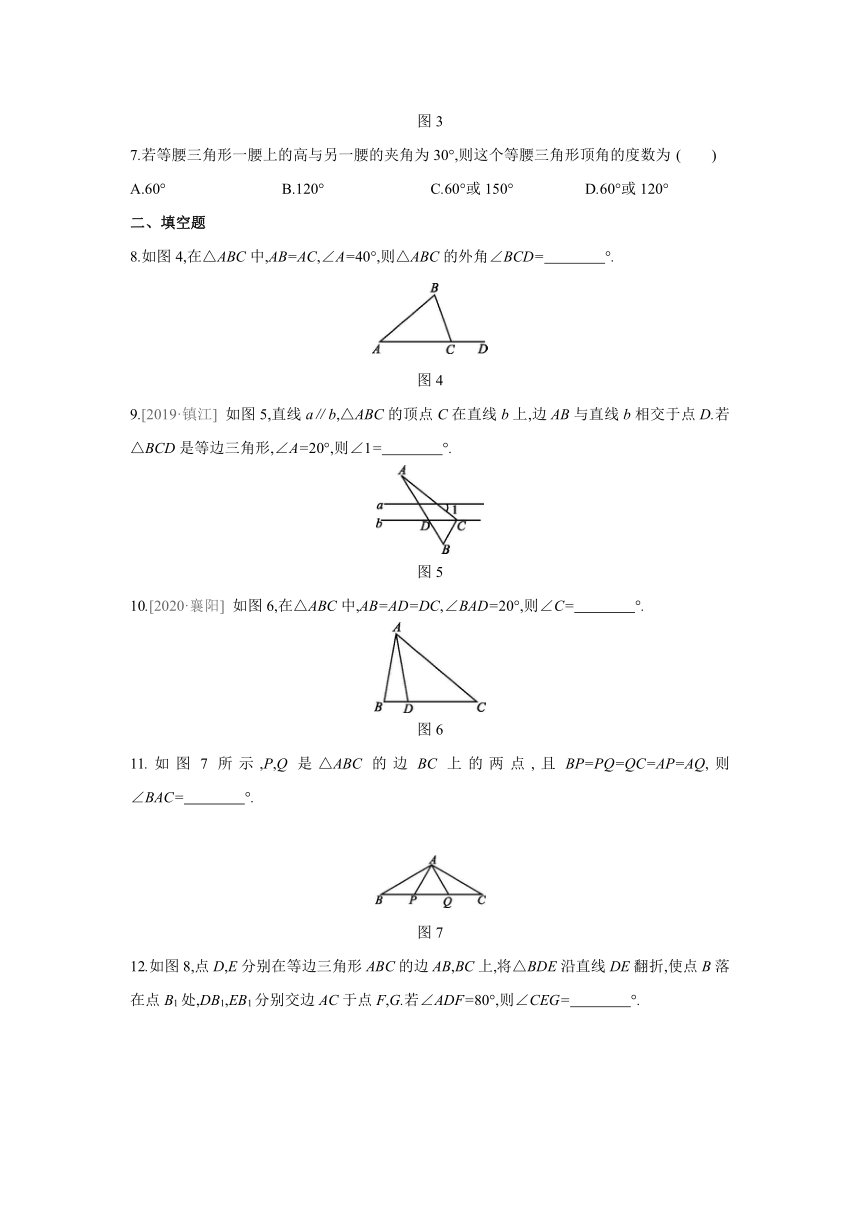
8.如图4,在△ABC中,AB=AC,∠A=40°,则△ABC的外角∠BCD= °.?
图4
9.[2019·镇江]
如图5,直线a∥b,△ABC的顶点C在直线b上,边AB与直线b相交于点D.若△BCD是等边三角形,∠A=20°,则∠1= °.?
图5
10.[2020·襄阳]
如图6,在△ABC中,AB=AD=DC,∠BAD=20°,则∠C= °.?
图6
11.如图7所示,P,Q是△ABC的边BC上的两点,且BP=PQ=QC=AP=AQ,则∠BAC= °.?
图7
12.如图8,点D,E分别在等边三角形ABC的边AB,BC上,将△BDE沿直线DE翻折,使点B落在点B1处,DB1,EB1分别交边AC于点F,G.若∠ADF=80°,则∠CEG= °.
图8
三、解答题
13.如图9,在△ABC中,AB=AC,AD⊥BC于点D.若AB=5,BD=4,求△ABC的周长.
图9
14.如图10,已知AB=AC=AD,且AD∥BC.求证:∠DAC=2∠D.
图10
15.如图11,△ABC和△ADE都是等边三角形,AD是BC边上的中线.
求证:BE=BD.
图11
16.如图12所示,在△ABC中,AB=AC,D是BA延长线上一点,点E在AC上,且AD=AE,则DE与BC有什么位置关系?试说明理由.
图12
17.小华在证明命题“等腰三角形底边的中点到两腰的距离相等”时,已经画图(如图13)并写出了如下的已知、求证,请帮她完成证明过程.(用两种方法)
已知:在△ABC中,AB=AC,D为BC的中点,DE⊥AB于点E,DF⊥AC于点F.
求证:DE=DF.
图13
答案
1.[解析]
A 等腰三角形的高、中线和角平分线都是线段,而对称轴是直线,所以选项B,C,D都不对;等腰三角形的对称轴是底边上的高所在的直线,选项A对.故选A.
2.D
3.[解析]
C 由于题中没有指明哪条边是底,哪条边是腰,所以应该分两种情况讨论:①若4是腰长,则三角形的三边长分别为4,4,2,能组成三角形,所以第三边的长为4;②若4是底边长,则三角形的三边长分别为2,2,4,∵2+2=4,∴不能组成三角形.综上,第三边的长为4.故选C.
4.[解析]
D 80°的角可作底角,也可作顶角,故分两种情况:①若80°的角是顶角,则两个底角的度数是50°,50°;②若80°的角是底角,则顶角的度数是20°.所以三角形其余两个内角的度数分别为50°,50°或80°,20°.故选D.
5.[解析]
C ∵AB=AC,∠A=36°,∴∠ABC=∠ACB=72°.
∵BD平分∠ABC,
∴∠ABD=∠ABC=×72°=36°,∴∠BDC=∠A+∠ABD=36°+36°=72°,∠ABD=∠A,∴∠DCB=∠BDC,AD=BD,∴BD=BC=b,∴AD=BD=b,∴CD=AC-AD=a-b.故选C.
6.[解析]
C ∵在等边三角形ABC中,AD⊥BC,∴AD是∠BAC的平分线和BC边上的中线,∴∠CAD=∠BAC=30°.∵∠CED=50°,∴∠ACE=∠CED-∠CAD=50°-30°=20°.易证△ABE≌△ACE,∴∠ABE=∠ACE=20°.故选C.
7.D 8.110
9.[答案]
40
[解析]
如图.∵△BCD是等边三角形,∴∠BDC=60°.∵a∥b,∴∠2=∠BDC=60°.由三角形的外角的性质可知,∠1的对顶角=∠2-∠A=40°.故答案为40.
10.[答案]
40
[解析]
∵AB=AD=DC,∴∠ABD=∠ADB,∠DAC=∠C.∵∠BAD=20°,∴∠ADB==80°.又∵∠ADB=∠DAC+∠C,∴∠C=∠ADB=40°.故答案为40.
11.[答案]
120
[解析]
由题意,得△PAQ为等边三角形,所以∠APQ=∠AQP=60°,利用三角形外角的性质可得∠BAP=∠QAC=30°,故∠BAC=120°.
12.[答案]
40
[解析]
由翻折可得∠BDE=∠EDF,
∠BED=∠DEG.
∵∠ADF=80°,
∴∠BDE=∠EDF=50°.
又∵∠B=60°,
∴∠BED=∠DEG=70°,
∴∠CEG=180°-70°-70°=40°.
13.解:∵AB=AC,AD⊥BC,AB=5,BD=4,
∴AC=5,DC=BD=4,
∴BC=8,
∴△ABC的周长为AB+AC+BC=5+5+8=18.
14.证明:∵AB=AC=AD,
∴∠C=∠ABC,∠D=∠ABD,
∴∠ABC=∠CBD+∠ABD=∠CBD+∠D.
∵AD∥BC,
∴∠CBD=∠D,∠DAC=∠C,
∴∠ABC=∠D+∠D=2∠D.
∵∠C=∠ABC,∠DAC=∠C,
∴∠DAC=∠ABC=2∠D.
15.证明:∵△ABC和△ADE都是等边三角形,
∴AB=AC,AE=AD,∠BAC=∠DAE=60°.
∵AB=AC,AD为BC边上的中线,
∴∠BAD=∠CAD=∠BAC=30°,
∴∠BAE=∠DAE-∠BAD=30°=∠BAD.
在△ABE和△ABD中,
∵AE=AD,∠BAE=∠BAD,AB=AB,
∴△ABE≌△ABD(S.A.S.),
∴BE=BD.
16.解:DE与BC的位置关系是DE⊥BC.
理由如下:过点A作AF⊥BC于点F.
∵AB=AC,∴∠BAF=∠CAF.
∵AD=AE,∴∠AED=∠D,
∴∠BAC=∠D+∠AED=2∠D,
∴2∠BAF=2∠D,即∠BAF=∠D,
∴DE∥AF.
又∵AF⊥BC,∴DE⊥BC.
17.证明:(方法不唯一,以下方法供参考)
方法一:∵AB=AC,∴∠B=∠C.
∵DE⊥AB,DF⊥AC,
∴∠BED=∠CFD=90°.
∵D是BC的中点,
∴BD=CD.
在△BED与△CFD中,
∵∠BED=∠CFD,∠B=∠C,BD=CD,
∴△BED≌△CFD(A.A.S.),∴DE=DF.
方法二:如图,连结AD.
∵AB=AC,D为BC的中点,
∴AD为∠BAC的平分线,
∴∠EAD=∠FAD.
∵DE⊥AB,DF⊥AC,
∴∠AED=∠AFD=90°.
在△ADE和△ADF中,
∵∠AED=∠AFD,∠EAD=∠FAD,
AD=AD,
∴△ADE≌△ADF(A.A.S.),
∴DE=DF.
方法三:如图,连结AD.
∵AB=AC,D为BC的中点,
∴AD⊥BC,S△ABD=S△ACD,
∴AB·DE=AC·DF.
又∵AB=AC,∴DE=DF.
1.等腰三角形的性质
一、选择题
1.等腰三角形的对称轴是
( )
A.底边上的高所在的直线
B.底边上的高
C.底边上的中线
D.顶角平分线
2.如图1,在△ABC中,AB=AC,D是BC边的中点,则下列结论中不正确的是
( )
A.∠B=∠C
B.AD⊥BC
C.AD平分∠BAC
D.AB=2BD
图1
3.[2019·抚顺]
若一个等腰三角形的两边长分别为2,4,则第三边的长为
( )
A.2
B.3
C.4
D.2或4
4.若等腰三角形的一个内角为80°,则此三角形其余两个内角的度数分别为
( )
A.50°,50°
B.80°,20°
C.80°,50°
D.50°,50°或80°,20°
5.[2020·南充]
如图2,在等腰三角形ABC中,BD为∠ABC的平分线,∠A=36°,AB=AC=a,BC=b,则CD等于
( )
A.
B.
C.a-b
D.b-a
图2
6.如图3,在等边三角形ABC中,AD⊥BC于点D,E为AD上一点,∠CED=50°,则∠ABE等于
( )
A.10°
B.15°
C.20°
D.25°
图3
7.若等腰三角形一腰上的高与另一腰的夹角为30°,则这个等腰三角形顶角的度数为
( )
A.60°
B.120°
C.60°或150°
D.60°或120°
二、填空题
8.如图4,在△ABC中,AB=AC,∠A=40°,则△ABC的外角∠BCD= °.?
图4
9.[2019·镇江]
如图5,直线a∥b,△ABC的顶点C在直线b上,边AB与直线b相交于点D.若△BCD是等边三角形,∠A=20°,则∠1= °.?
图5
10.[2020·襄阳]
如图6,在△ABC中,AB=AD=DC,∠BAD=20°,则∠C= °.?
图6
11.如图7所示,P,Q是△ABC的边BC上的两点,且BP=PQ=QC=AP=AQ,则∠BAC= °.?
图7
12.如图8,点D,E分别在等边三角形ABC的边AB,BC上,将△BDE沿直线DE翻折,使点B落在点B1处,DB1,EB1分别交边AC于点F,G.若∠ADF=80°,则∠CEG= °.
图8
三、解答题
13.如图9,在△ABC中,AB=AC,AD⊥BC于点D.若AB=5,BD=4,求△ABC的周长.
图9
14.如图10,已知AB=AC=AD,且AD∥BC.求证:∠DAC=2∠D.
图10
15.如图11,△ABC和△ADE都是等边三角形,AD是BC边上的中线.
求证:BE=BD.
图11
16.如图12所示,在△ABC中,AB=AC,D是BA延长线上一点,点E在AC上,且AD=AE,则DE与BC有什么位置关系?试说明理由.
图12
17.小华在证明命题“等腰三角形底边的中点到两腰的距离相等”时,已经画图(如图13)并写出了如下的已知、求证,请帮她完成证明过程.(用两种方法)
已知:在△ABC中,AB=AC,D为BC的中点,DE⊥AB于点E,DF⊥AC于点F.
求证:DE=DF.
图13
答案
1.[解析]
A 等腰三角形的高、中线和角平分线都是线段,而对称轴是直线,所以选项B,C,D都不对;等腰三角形的对称轴是底边上的高所在的直线,选项A对.故选A.
2.D
3.[解析]
C 由于题中没有指明哪条边是底,哪条边是腰,所以应该分两种情况讨论:①若4是腰长,则三角形的三边长分别为4,4,2,能组成三角形,所以第三边的长为4;②若4是底边长,则三角形的三边长分别为2,2,4,∵2+2=4,∴不能组成三角形.综上,第三边的长为4.故选C.
4.[解析]
D 80°的角可作底角,也可作顶角,故分两种情况:①若80°的角是顶角,则两个底角的度数是50°,50°;②若80°的角是底角,则顶角的度数是20°.所以三角形其余两个内角的度数分别为50°,50°或80°,20°.故选D.
5.[解析]
C ∵AB=AC,∠A=36°,∴∠ABC=∠ACB=72°.
∵BD平分∠ABC,
∴∠ABD=∠ABC=×72°=36°,∴∠BDC=∠A+∠ABD=36°+36°=72°,∠ABD=∠A,∴∠DCB=∠BDC,AD=BD,∴BD=BC=b,∴AD=BD=b,∴CD=AC-AD=a-b.故选C.
6.[解析]
C ∵在等边三角形ABC中,AD⊥BC,∴AD是∠BAC的平分线和BC边上的中线,∴∠CAD=∠BAC=30°.∵∠CED=50°,∴∠ACE=∠CED-∠CAD=50°-30°=20°.易证△ABE≌△ACE,∴∠ABE=∠ACE=20°.故选C.
7.D 8.110
9.[答案]
40
[解析]
如图.∵△BCD是等边三角形,∴∠BDC=60°.∵a∥b,∴∠2=∠BDC=60°.由三角形的外角的性质可知,∠1的对顶角=∠2-∠A=40°.故答案为40.
10.[答案]
40
[解析]
∵AB=AD=DC,∴∠ABD=∠ADB,∠DAC=∠C.∵∠BAD=20°,∴∠ADB==80°.又∵∠ADB=∠DAC+∠C,∴∠C=∠ADB=40°.故答案为40.
11.[答案]
120
[解析]
由题意,得△PAQ为等边三角形,所以∠APQ=∠AQP=60°,利用三角形外角的性质可得∠BAP=∠QAC=30°,故∠BAC=120°.
12.[答案]
40
[解析]
由翻折可得∠BDE=∠EDF,
∠BED=∠DEG.
∵∠ADF=80°,
∴∠BDE=∠EDF=50°.
又∵∠B=60°,
∴∠BED=∠DEG=70°,
∴∠CEG=180°-70°-70°=40°.
13.解:∵AB=AC,AD⊥BC,AB=5,BD=4,
∴AC=5,DC=BD=4,
∴BC=8,
∴△ABC的周长为AB+AC+BC=5+5+8=18.
14.证明:∵AB=AC=AD,
∴∠C=∠ABC,∠D=∠ABD,
∴∠ABC=∠CBD+∠ABD=∠CBD+∠D.
∵AD∥BC,
∴∠CBD=∠D,∠DAC=∠C,
∴∠ABC=∠D+∠D=2∠D.
∵∠C=∠ABC,∠DAC=∠C,
∴∠DAC=∠ABC=2∠D.
15.证明:∵△ABC和△ADE都是等边三角形,
∴AB=AC,AE=AD,∠BAC=∠DAE=60°.
∵AB=AC,AD为BC边上的中线,
∴∠BAD=∠CAD=∠BAC=30°,
∴∠BAE=∠DAE-∠BAD=30°=∠BAD.
在△ABE和△ABD中,
∵AE=AD,∠BAE=∠BAD,AB=AB,
∴△ABE≌△ABD(S.A.S.),
∴BE=BD.
16.解:DE与BC的位置关系是DE⊥BC.
理由如下:过点A作AF⊥BC于点F.
∵AB=AC,∴∠BAF=∠CAF.
∵AD=AE,∴∠AED=∠D,
∴∠BAC=∠D+∠AED=2∠D,
∴2∠BAF=2∠D,即∠BAF=∠D,
∴DE∥AF.
又∵AF⊥BC,∴DE⊥BC.
17.证明:(方法不唯一,以下方法供参考)
方法一:∵AB=AC,∴∠B=∠C.
∵DE⊥AB,DF⊥AC,
∴∠BED=∠CFD=90°.
∵D是BC的中点,
∴BD=CD.
在△BED与△CFD中,
∵∠BED=∠CFD,∠B=∠C,BD=CD,
∴△BED≌△CFD(A.A.S.),∴DE=DF.
方法二:如图,连结AD.
∵AB=AC,D为BC的中点,
∴AD为∠BAC的平分线,
∴∠EAD=∠FAD.
∵DE⊥AB,DF⊥AC,
∴∠AED=∠AFD=90°.
在△ADE和△ADF中,
∵∠AED=∠AFD,∠EAD=∠FAD,
AD=AD,
∴△ADE≌△ADF(A.A.S.),
∴DE=DF.
方法三:如图,连结AD.
∵AB=AC,D为BC的中点,
∴AD⊥BC,S△ABD=S△ACD,
∴AB·DE=AC·DF.
又∵AB=AC,∴DE=DF.
