2021_2022学年八年级数学上册第13章全等三角形13.24第1课时角边角同步练习新版华东师大版
文档属性
| 名称 | 2021_2022学年八年级数学上册第13章全等三角形13.24第1课时角边角同步练习新版华东师大版 |

|
|
| 格式 | docx | ||
| 文件大小 | 214.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-07 00:00:00 | ||
图片预览

文档简介
13.2 4.第1课时 角边角
一、选择题
1.如图1,四个三角形中,全等三角形是 ( )
图1
A.②与③ B.②与④ C.①与② D.③与④
2.已知AB=A'B',∠A=∠A',∠B=∠B',则△ABC≌△A'B'C'的根据是 ( )
A.S.A.S. B.S.S.A.
C.A.S.A. D.A.A.S.
3.如图,一定全等的两个三角形是 ( )
A.①② B.①③ C.②③ D.以上都不对
4.如图所示,下列各组条件中,能判定△ABC≌△DEF的是 ( )
A.AB=DE,BC=EF,∠A=∠D
B.∠A=∠D,BC=EF,AC=DF
C.∠A=∠D,∠C=∠F,AC=DF
D.∠A=∠D,∠B=∠E,∠C=∠F
109093016510
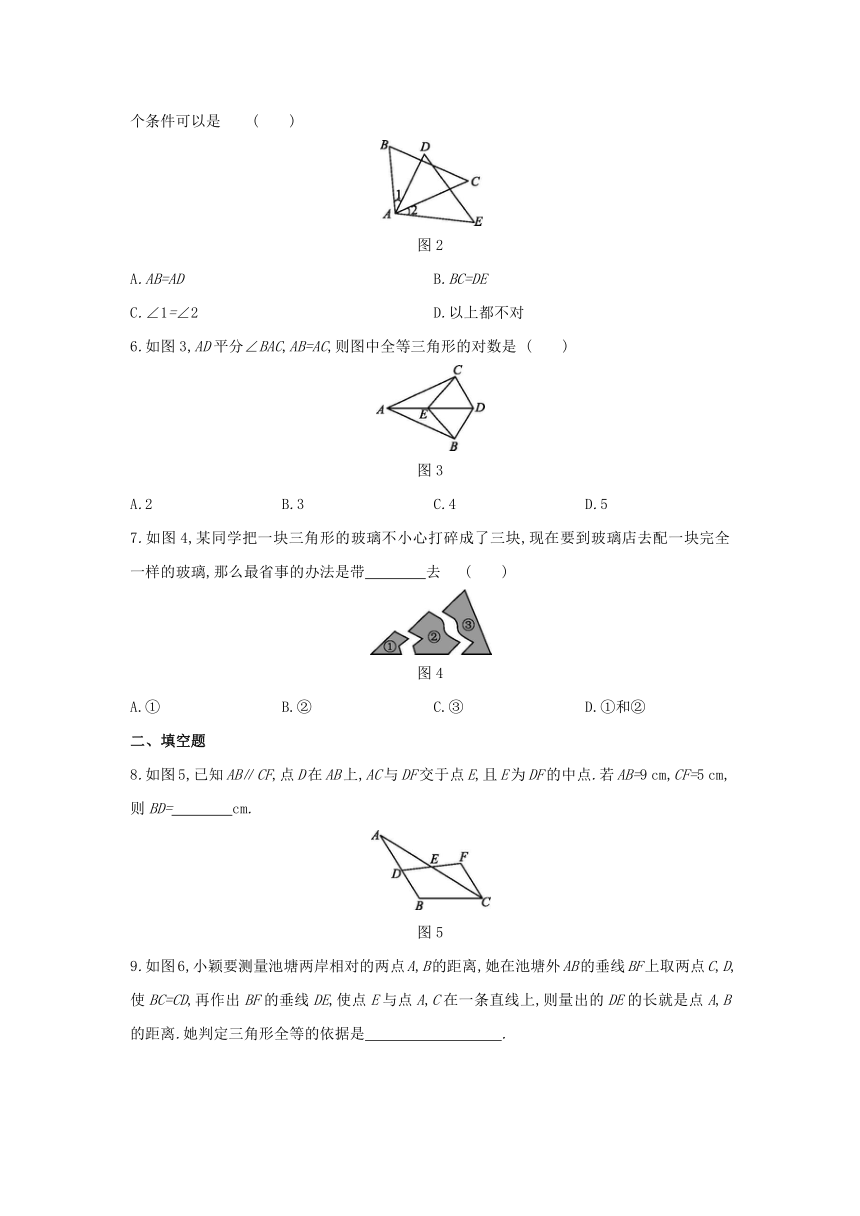
5.如图2,已知∠C=∠E,AC=AE,欲利用“A.S.A.”证明△ABC≌△ADE,只需补充一个条件,这个条件可以是 ( )
图2
A.AB=AD B.BC=DE
C.∠1=∠2 D.以上都不对
6.如图3,AD平分∠BAC,AB=AC,则图中全等三角形的对数是 ( )
图3
A.2 B.3 C.4 D.5
7.如图4,某同学把一块三角形的玻璃不小心打碎成了三块,现在要到玻璃店去配一块完全一样的玻璃,那么最省事的办法是带 去 ( )?
图4
A.① B.② C.③ D.①和②
二、填空题
8.如图5,已知AB∥CF,点D在AB上,AC与DF交于点E,且E为DF的中点.若AB=9 cm,CF=5 cm,则BD= cm.?
图5
9.如图6,小颖要测量池塘两岸相对的两点A,B的距离,她在池塘外AB的垂线BF上取两点C,D,使BC=CD,再作出BF的垂线DE,使点E与点A,C在一条直线上,则量出的DE的长就是点A,B的距离.她判定三角形全等的依据是 .
图6
三、解答题
305371530353010.如图所示,点E在△ABC外部,点D在BC边上,DE交AC于点F,若∠1=∠2,∠E=∠C,AE=AC.求证:△ABC≌△ADE.
11.已知:如图7,AC=AE,∠C=∠E,∠1=∠2,求证:△ABC≌△ADE.
图7
12.如图8,点B,C,D在同一条直线上,AB⊥BD,DE⊥BD,AC⊥CE,垂足分别为B,D,C,且AB=CD.
(1)求证:△ABC≌△CDE;
(2)若AB=2,DE=3,求BD的长.
图8
13.如图9所示,太阳光线AB和A'B'是平行的,地面上甲、乙两人在阳光照射下的影子一样长,那么甲、乙两人一样高吗?说明理由.
图9
答案
1. D 2.C 3.B 4.C 5.C 6.B 7.C
8.[答案] 4
[解析] 由条件可得△AED≌△CEF,所以AD=CF=5 cm,则BD=9-5=4(cm).
9.A.S.A.(或“角边角”)
10.证明:∵∠1=∠2,∴∠1+∠DAC=∠2+∠DAC,
即∠BAC=∠DAE.
在△ABC和△ADE中,
∵∠BAC=∠DAE,AC=AE,∠C=∠E,
∴△ABC≌△ADE(A.S.A.).
11.证明:∵∠1=∠2,
∴∠EAC+∠1=∠EAC+∠2,
即∠BAC=∠DAE.
又∵AC=AE,∠C=∠E,
∴△ABC≌△ADE(A.S.A.).
12.解:(1)证明:∵AB⊥BD,DE⊥BD,AC⊥CE,
∴∠B=∠D=∠ACE=90°,
∴∠BAC+∠ACB=90°,∠ACB+∠DCE=90°,
∴∠BAC=∠DCE.
在△ABC和△CDE中,
∵∠B=∠D,AB=CD,∠BAC=∠DCE,
∴△ABC≌△CDE(A.S.A.).
(2)∵△ABC≌△CDE,
∴BC=DE=3,CD=AB=2,∴BD=5.
13.解:一样高.理由如下:
如图,分别过点A,A'作AC⊥BB',交直线BB'于点C,A'C'⊥BB',交BB'于点C',
则∠ACB=∠A'C'B'=90°,BC=B'C'.
∵AB∥A'B',∴∠ABC=∠A'B'C'.
在△ABC和△A'B'C'中,
∵∠ACB=∠A'C'B',BC=B'C',∠ABC=∠A'B'C',∴△ABC≌△A'B'C'(A.S.A.),
∴AC=A'C',即甲、乙两人一样高.
一、选择题
1.如图1,四个三角形中,全等三角形是 ( )
图1
A.②与③ B.②与④ C.①与② D.③与④
2.已知AB=A'B',∠A=∠A',∠B=∠B',则△ABC≌△A'B'C'的根据是 ( )
A.S.A.S. B.S.S.A.
C.A.S.A. D.A.A.S.
3.如图,一定全等的两个三角形是 ( )
A.①② B.①③ C.②③ D.以上都不对
4.如图所示,下列各组条件中,能判定△ABC≌△DEF的是 ( )
A.AB=DE,BC=EF,∠A=∠D
B.∠A=∠D,BC=EF,AC=DF
C.∠A=∠D,∠C=∠F,AC=DF
D.∠A=∠D,∠B=∠E,∠C=∠F
109093016510
5.如图2,已知∠C=∠E,AC=AE,欲利用“A.S.A.”证明△ABC≌△ADE,只需补充一个条件,这个条件可以是 ( )
图2
A.AB=AD B.BC=DE
C.∠1=∠2 D.以上都不对
6.如图3,AD平分∠BAC,AB=AC,则图中全等三角形的对数是 ( )
图3
A.2 B.3 C.4 D.5
7.如图4,某同学把一块三角形的玻璃不小心打碎成了三块,现在要到玻璃店去配一块完全一样的玻璃,那么最省事的办法是带 去 ( )?
图4
A.① B.② C.③ D.①和②
二、填空题
8.如图5,已知AB∥CF,点D在AB上,AC与DF交于点E,且E为DF的中点.若AB=9 cm,CF=5 cm,则BD= cm.?
图5
9.如图6,小颖要测量池塘两岸相对的两点A,B的距离,她在池塘外AB的垂线BF上取两点C,D,使BC=CD,再作出BF的垂线DE,使点E与点A,C在一条直线上,则量出的DE的长就是点A,B的距离.她判定三角形全等的依据是 .
图6
三、解答题
305371530353010.如图所示,点E在△ABC外部,点D在BC边上,DE交AC于点F,若∠1=∠2,∠E=∠C,AE=AC.求证:△ABC≌△ADE.
11.已知:如图7,AC=AE,∠C=∠E,∠1=∠2,求证:△ABC≌△ADE.
图7
12.如图8,点B,C,D在同一条直线上,AB⊥BD,DE⊥BD,AC⊥CE,垂足分别为B,D,C,且AB=CD.
(1)求证:△ABC≌△CDE;
(2)若AB=2,DE=3,求BD的长.
图8
13.如图9所示,太阳光线AB和A'B'是平行的,地面上甲、乙两人在阳光照射下的影子一样长,那么甲、乙两人一样高吗?说明理由.
图9
答案
1. D 2.C 3.B 4.C 5.C 6.B 7.C
8.[答案] 4
[解析] 由条件可得△AED≌△CEF,所以AD=CF=5 cm,则BD=9-5=4(cm).
9.A.S.A.(或“角边角”)
10.证明:∵∠1=∠2,∴∠1+∠DAC=∠2+∠DAC,
即∠BAC=∠DAE.
在△ABC和△ADE中,
∵∠BAC=∠DAE,AC=AE,∠C=∠E,
∴△ABC≌△ADE(A.S.A.).
11.证明:∵∠1=∠2,
∴∠EAC+∠1=∠EAC+∠2,
即∠BAC=∠DAE.
又∵AC=AE,∠C=∠E,
∴△ABC≌△ADE(A.S.A.).
12.解:(1)证明:∵AB⊥BD,DE⊥BD,AC⊥CE,
∴∠B=∠D=∠ACE=90°,
∴∠BAC+∠ACB=90°,∠ACB+∠DCE=90°,
∴∠BAC=∠DCE.
在△ABC和△CDE中,
∵∠B=∠D,AB=CD,∠BAC=∠DCE,
∴△ABC≌△CDE(A.S.A.).
(2)∵△ABC≌△CDE,
∴BC=DE=3,CD=AB=2,∴BD=5.
13.解:一样高.理由如下:
如图,分别过点A,A'作AC⊥BB',交直线BB'于点C,A'C'⊥BB',交BB'于点C',
则∠ACB=∠A'C'B'=90°,BC=B'C'.
∵AB∥A'B',∴∠ABC=∠A'B'C'.
在△ABC和△A'B'C'中,
∵∠ACB=∠A'C'B',BC=B'C',∠ABC=∠A'B'C',∴△ABC≌△A'B'C'(A.S.A.),
∴AC=A'C',即甲、乙两人一样高.
