2021_2022学年八年级数学上册第13章全等三角形13.23边角边同步练习新版华东师大版
文档属性
| 名称 | 2021_2022学年八年级数学上册第13章全等三角形13.23边角边同步练习新版华东师大版 |
|
|
| 格式 | docx | ||
| 文件大小 | 207.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-07 10:35:14 | ||
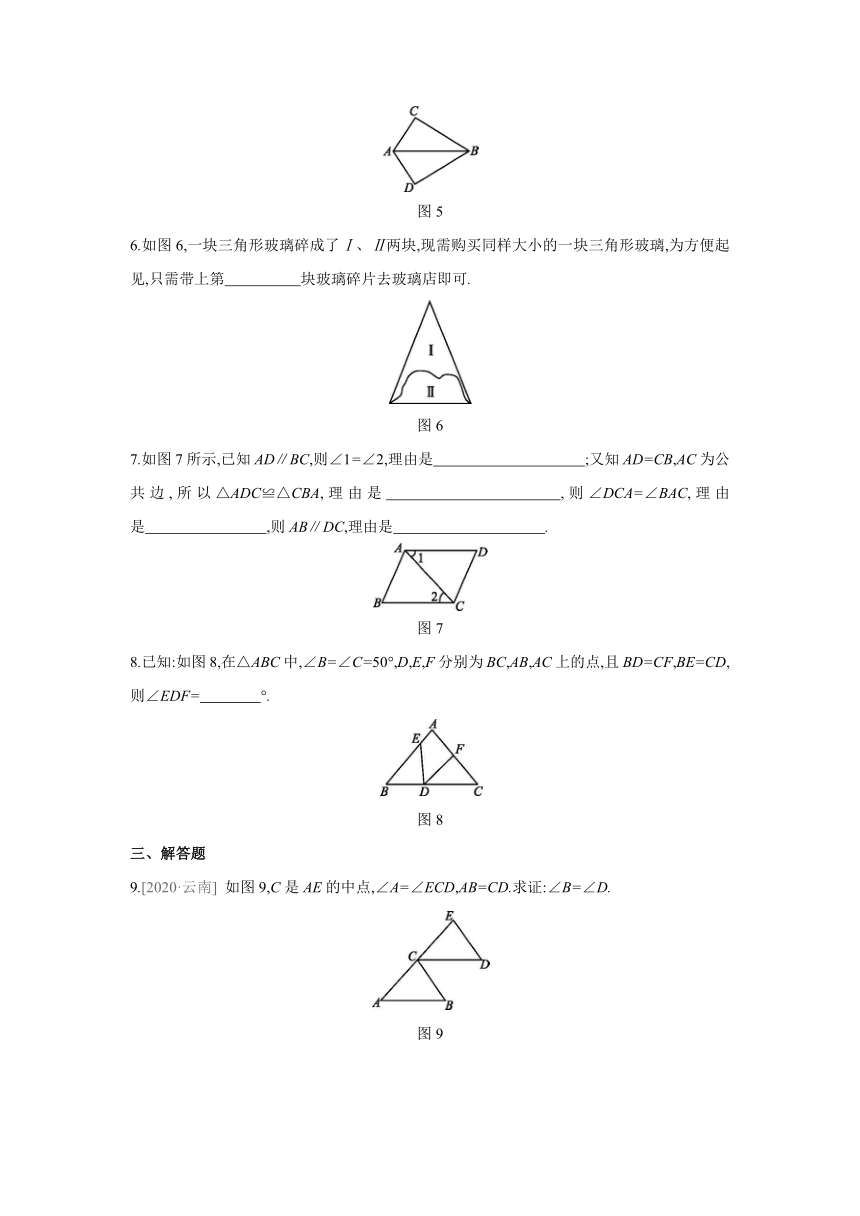
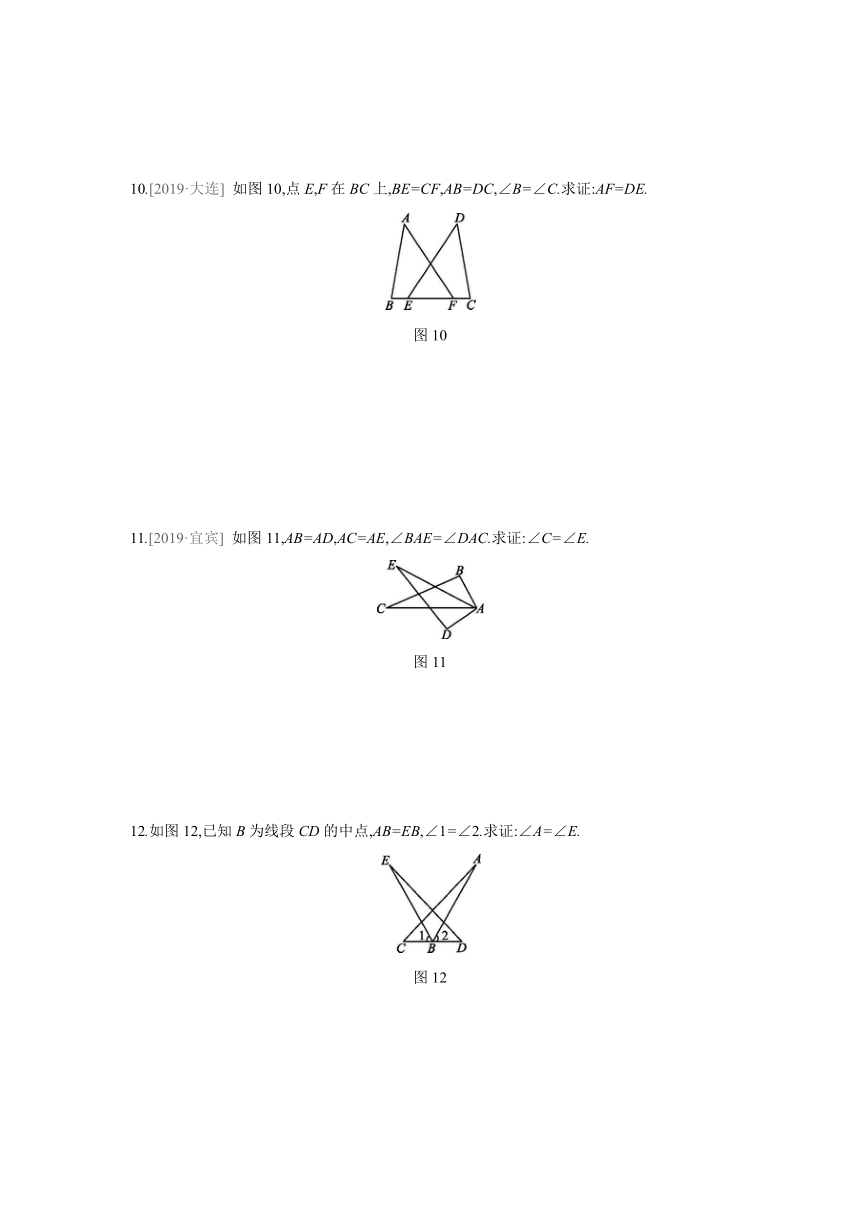
图片预览

文档简介
13.2.3
边角边
一、选择题
1.如图1,下列三角形中一定全等的是
( )
图1
A.①②
B.②③
C.③④
D.①④
2.如图2,已知BC=EC,AC=DC,要判定△ABC≌△DEC,则可以添加的条件是
( )
图2
A.∠BCE=∠ACD
B.∠BCE=∠ACE
C.∠A=∠D
D.∠B=∠E
3.如图3所示,点E,C在BF上,AB∥DE,AB=DE,BE=CF,∠B=32°,∠A=78°,则∠F等于
( )
图3
A.55°
B.65°
C.60°
D.70°
4.如图4,已知AC⊥BD于点O,OB=OD,则图中全等的三角形共有
( )
图4
A.2对
B.3对
C.4对
D.5对
二、填空题
5.如图5,AC=AD,请你添加一个条件,可以根据“边角边”判定△ADB≌△ACB,你所添加的条件是 .?
图5
6.如图6,一块三角形玻璃碎成了Ⅰ、Ⅱ两块,现需购买同样大小的一块三角形玻璃,为方便起见,只需带上第 块玻璃碎片去玻璃店即可.
图6
7.如图7所示,已知AD∥BC,则∠1=∠2,理由是 ;又知AD=CB,AC为公共边,所以△ADC≌△CBA,理由是 ,则∠DCA=∠BAC,理由是 ,则AB∥DC,理由是 .?
图7
8.已知:如图8,在△ABC中,∠B=∠C=50°,D,E,F分别为BC,AB,AC上的点,且BD=CF,BE=CD,则∠EDF= °.?
图8
三、解答题
9.[2020·云南]
如图9,C是AE的中点,∠A=∠ECD,AB=CD.求证:∠B=∠D.
图9
10.[2019·大连]
如图10,点E,F在BC上,BE=CF,AB=DC,∠B=∠C.求证:AF=DE.
图10
11.[2019·宜宾]
如图11,AB=AD,AC=AE,∠BAE=∠DAC.求证:∠C=∠E.
图11
12.如图12,已知B为线段CD的中点,AB=EB,∠1=∠2.求证:∠A=∠E.
图12
13.如图13,点A,D,F,B在同一直线上,AD=BF,AE=BC,且AE∥BC.EF与CD有怎样的关系?请说明理由.
图13
14.[2020·徐州]
如图14,AC⊥BC,DC⊥EC,AC=BC,DC=EC,AE与BD交于点F.
(1)求证:AE=BD;
(2)求∠AFD的度数.
图14
15.如图15,在△ABC中,∠BAC=∠B=60°,AB=CA,点D,E分别是边BC,AB所在直线上的动点,且BD=AE,AD与CE交于点F.
(1)当点D,E分别在边BC,AB上运动时,∠DFC的度数是否发生变化?若不变,求出其度数;若变化,写出其变化规律.
(2)当点D,E分别运动到CB,BA的延长线上时,(1)中的结论是否改变?说明理由.
图15
答案
1.A 2.A
3.[解析]
D 因为AB∥DE,所以∠B=∠DEF.又由BE=CF可知BC=EF.结合AB=DE,可由“S.A.S.”判定△ABC≌△DEF,所以∠F=∠ACB=180°-(∠A+∠B)=180°-(78°+32°)=70°.
4.[解析]
B 由AC⊥BD,OB=OD可得△AOB≌△AOD,△BOC≌△DOC;而由△AOB≌△AOD可得AB=AD,∠BAC=∠DAC,再根据AC=AC,可得△BAC≌△DAC.
5.∠CAB=∠DAB
6.Ⅰ
7.两直线平行,内错角相等 S.A.S. 全等三角形的对应角相等 内错角相等,两直线平行
8.[答案]
50
[解析]
由“S.A.S.”可知△BDE≌△CFD,
∴∠BED=∠CDF.
∵∠EDF=∠EDC-∠CDF,∠B=∠EDC-∠BED,∴∠EDF=∠B=50°.
9.证明:∵C是AE的中点,
∴AC=CE.
在△ABC和△CDE中,∵AC=CE,∠A=∠ECD,AB=CD,
∴△ABC≌△CDE(S.A.S.),
∴∠B=∠D.
10.证明:∵BE=CF,
∴BE+EF=CF+EF,即BF=CE.
在△ABF和△DCE中,
∵AB=DC,∠B=∠C,BF=CE,
∴△ABF≌△DCE(S.A.S.),
∴AF=DE.
11.证明:∵∠BAE=∠DAC,
∴∠BAE+∠CAE=∠DAC+∠CAE,
即∠CAB=∠EAD.
在△ABC和△ADE中,
∵AB=AD,∠CAB=∠EAD,AC=AE,
∴△ABC≌△ADE(S.A.S.),
∴∠C=∠E.
12.证明:∵∠1=∠2,∠1+∠EBD=180°,∠2+∠ABC=180°,
∴∠ABC=∠EBD.
∵B为CD的中点,∴BC=BD.
在△ABC和△EBD中,
∵BC=BD,∠ABC=∠EBD,AB=EB,
∴△ABC≌△EBD(S.A.S.),∴∠A=∠E.
13.解:EF=CD,EF∥CD.
理由:由AE∥BC得∠A=∠B.
由AD=BF,得AF=BD.
在△AEF和△BCD中,因为AF=BD,∠A=∠B,AE=BC,
所以△AEF≌△BCD,
所以EF=CD,∠AFE=∠BDC,
所以EF∥CD.
14.解:(1)证明:∵AC⊥BC,DC⊥EC,
∴∠ACB=∠DCE=90°,
∴∠ACE=∠BCD.
在△ACE和△BCD中,∵AC=BC,∠ACE=∠BCD,EC=DC,
∴△ACE≌△BCD(S.A.S.),
∴AE=BD.
(2)如图,设AE与BC交于点N.
∵∠ACB=90°,∴∠A+∠ANC=90°.
∵△ACE≌△BCD,∴∠A=∠B.
又∵∠ANC=∠BNF,
∴∠AFD=∠B+∠BNF=∠A+∠ANC=90°.
15.解:(1)在△ABD和△CAE中,∵AB=CA,∠B=∠BAC,BD=AE,
∴△ABD≌△CAE(S.A.S.),
∴∠BAD=∠ACE,
∴∠DFC=∠ACF+∠FAC=∠BAD+∠FAC=∠BAC=60°,
∴∠DFC的度数不发生变化,度数始终为60°.
(2)(1)中的结论不改变.理由:如图所示,
∵∠ABC=∠BAC=60°,
∴∠ABD=∠CAE=120°.
在△ABD和△CAE中,∵AB=CA,∠ABD=∠CAE,BD=AE,
∴△ABD≌△CAE,∴∠D=∠E,
∴∠DFC=∠E+∠EAF=∠D+∠DAB=∠ABC=60°.
边角边
一、选择题
1.如图1,下列三角形中一定全等的是
( )
图1
A.①②
B.②③
C.③④
D.①④
2.如图2,已知BC=EC,AC=DC,要判定△ABC≌△DEC,则可以添加的条件是
( )
图2
A.∠BCE=∠ACD
B.∠BCE=∠ACE
C.∠A=∠D
D.∠B=∠E
3.如图3所示,点E,C在BF上,AB∥DE,AB=DE,BE=CF,∠B=32°,∠A=78°,则∠F等于
( )
图3
A.55°
B.65°
C.60°
D.70°
4.如图4,已知AC⊥BD于点O,OB=OD,则图中全等的三角形共有
( )
图4
A.2对
B.3对
C.4对
D.5对
二、填空题
5.如图5,AC=AD,请你添加一个条件,可以根据“边角边”判定△ADB≌△ACB,你所添加的条件是 .?
图5
6.如图6,一块三角形玻璃碎成了Ⅰ、Ⅱ两块,现需购买同样大小的一块三角形玻璃,为方便起见,只需带上第 块玻璃碎片去玻璃店即可.
图6
7.如图7所示,已知AD∥BC,则∠1=∠2,理由是 ;又知AD=CB,AC为公共边,所以△ADC≌△CBA,理由是 ,则∠DCA=∠BAC,理由是 ,则AB∥DC,理由是 .?
图7
8.已知:如图8,在△ABC中,∠B=∠C=50°,D,E,F分别为BC,AB,AC上的点,且BD=CF,BE=CD,则∠EDF= °.?
图8
三、解答题
9.[2020·云南]
如图9,C是AE的中点,∠A=∠ECD,AB=CD.求证:∠B=∠D.
图9
10.[2019·大连]
如图10,点E,F在BC上,BE=CF,AB=DC,∠B=∠C.求证:AF=DE.
图10
11.[2019·宜宾]
如图11,AB=AD,AC=AE,∠BAE=∠DAC.求证:∠C=∠E.
图11
12.如图12,已知B为线段CD的中点,AB=EB,∠1=∠2.求证:∠A=∠E.
图12
13.如图13,点A,D,F,B在同一直线上,AD=BF,AE=BC,且AE∥BC.EF与CD有怎样的关系?请说明理由.
图13
14.[2020·徐州]
如图14,AC⊥BC,DC⊥EC,AC=BC,DC=EC,AE与BD交于点F.
(1)求证:AE=BD;
(2)求∠AFD的度数.
图14
15.如图15,在△ABC中,∠BAC=∠B=60°,AB=CA,点D,E分别是边BC,AB所在直线上的动点,且BD=AE,AD与CE交于点F.
(1)当点D,E分别在边BC,AB上运动时,∠DFC的度数是否发生变化?若不变,求出其度数;若变化,写出其变化规律.
(2)当点D,E分别运动到CB,BA的延长线上时,(1)中的结论是否改变?说明理由.
图15
答案
1.A 2.A
3.[解析]
D 因为AB∥DE,所以∠B=∠DEF.又由BE=CF可知BC=EF.结合AB=DE,可由“S.A.S.”判定△ABC≌△DEF,所以∠F=∠ACB=180°-(∠A+∠B)=180°-(78°+32°)=70°.
4.[解析]
B 由AC⊥BD,OB=OD可得△AOB≌△AOD,△BOC≌△DOC;而由△AOB≌△AOD可得AB=AD,∠BAC=∠DAC,再根据AC=AC,可得△BAC≌△DAC.
5.∠CAB=∠DAB
6.Ⅰ
7.两直线平行,内错角相等 S.A.S. 全等三角形的对应角相等 内错角相等,两直线平行
8.[答案]
50
[解析]
由“S.A.S.”可知△BDE≌△CFD,
∴∠BED=∠CDF.
∵∠EDF=∠EDC-∠CDF,∠B=∠EDC-∠BED,∴∠EDF=∠B=50°.
9.证明:∵C是AE的中点,
∴AC=CE.
在△ABC和△CDE中,∵AC=CE,∠A=∠ECD,AB=CD,
∴△ABC≌△CDE(S.A.S.),
∴∠B=∠D.
10.证明:∵BE=CF,
∴BE+EF=CF+EF,即BF=CE.
在△ABF和△DCE中,
∵AB=DC,∠B=∠C,BF=CE,
∴△ABF≌△DCE(S.A.S.),
∴AF=DE.
11.证明:∵∠BAE=∠DAC,
∴∠BAE+∠CAE=∠DAC+∠CAE,
即∠CAB=∠EAD.
在△ABC和△ADE中,
∵AB=AD,∠CAB=∠EAD,AC=AE,
∴△ABC≌△ADE(S.A.S.),
∴∠C=∠E.
12.证明:∵∠1=∠2,∠1+∠EBD=180°,∠2+∠ABC=180°,
∴∠ABC=∠EBD.
∵B为CD的中点,∴BC=BD.
在△ABC和△EBD中,
∵BC=BD,∠ABC=∠EBD,AB=EB,
∴△ABC≌△EBD(S.A.S.),∴∠A=∠E.
13.解:EF=CD,EF∥CD.
理由:由AE∥BC得∠A=∠B.
由AD=BF,得AF=BD.
在△AEF和△BCD中,因为AF=BD,∠A=∠B,AE=BC,
所以△AEF≌△BCD,
所以EF=CD,∠AFE=∠BDC,
所以EF∥CD.
14.解:(1)证明:∵AC⊥BC,DC⊥EC,
∴∠ACB=∠DCE=90°,
∴∠ACE=∠BCD.
在△ACE和△BCD中,∵AC=BC,∠ACE=∠BCD,EC=DC,
∴△ACE≌△BCD(S.A.S.),
∴AE=BD.
(2)如图,设AE与BC交于点N.
∵∠ACB=90°,∴∠A+∠ANC=90°.
∵△ACE≌△BCD,∴∠A=∠B.
又∵∠ANC=∠BNF,
∴∠AFD=∠B+∠BNF=∠A+∠ANC=90°.
15.解:(1)在△ABD和△CAE中,∵AB=CA,∠B=∠BAC,BD=AE,
∴△ABD≌△CAE(S.A.S.),
∴∠BAD=∠ACE,
∴∠DFC=∠ACF+∠FAC=∠BAD+∠FAC=∠BAC=60°,
∴∠DFC的度数不发生变化,度数始终为60°.
(2)(1)中的结论不改变.理由:如图所示,
∵∠ABC=∠BAC=60°,
∴∠ABD=∠CAE=120°.
在△ABD和△CAE中,∵AB=CA,∠ABD=∠CAE,BD=AE,
∴△ABD≌△CAE,∴∠D=∠E,
∴∠DFC=∠E+∠EAF=∠D+∠DAB=∠ABC=60°.
