23.2 中心对称(2)
图片预览

文档简介
23.2 中心对称(2)
第8周5课时
教学目标
(1) 理解关于中心对称的两个图形,对称点所连线段都经过对称中心,而且被对称中心所平分;理解关于中心对称的两个图形是全等图形;掌握这两个性质的运用.
(2)复习中心对称的基本概念(中心对称、对称中心,关于中心的对称点),提出问题,让学生分组讨论解决问题,老师引导总结中心对称的基本性质.
(3)培养学生的艺术创作能力和初步的艺术欣赏能力,培养勇于探索的精神,树立学习的自信心。
重难点、
1.重点:中心对称的两条基本性质及其运用.
2.难点与关键:让学生合作讨论,得出中心对称的两条基本性质.
教学方法:自学引导、当堂达标
教学过程
一、示标导学
1、复习引入
(老师口问,学生口答)
(1).什么叫中心对称?什么叫对称中心?
(2).什么叫关于中心的对称点?
(3).请同学随便画一三角形,以三角形一顶点为对称中心,画出这个三角形关于这个对称中心的对称图形,并分组讨论能得到什么结论.
(每组推荐一人上台陈述,老师点评)
2、出示学习目标(略)
二、自学释疑
1、结合学习目标和自学提纲自学课本 ,5分钟之后回答下列问题 ,在自学的过程中有问题的小组内讨论。
2、(老师)在黑板上画一个三角形ABC,分两种情况作两个图形
(1)作△ABC一顶点为对称中心的对称图形;
(2)作关于一定点O为对称中心的对称图形.
第一步,画出△ABC.
第二步,以△ABC的C点(或O点)为中心,旋转180°画出△A′B′和△A′B′C′,如图1和用2所示.
( http: / / www. )
(1) (2)
从图1中可以得出△ABC与△A′B′C是全等三角形;
分别连接对称点AA′、BB′、CC′,点O在这些线段上且O平分这些线段.
下面,我们就以图2为例来证明这两个结论.
证明:(1)在△ABC和△A′B′C′中,
OA=OA′,OB=OB′,∠AOB=∠A′OB′
∴△AOB≌△A′OB′
∴AB=A′B′
同理可证:AC=A′C′,BC=B′C′
∴△ABC≌△A′B′C′
(2)点A′是点A绕点O旋转180°后得到的,即线段OA绕点O旋转180°得到线段OA′,所以点O在线段AA′上,且OA=OA′,即点O是线段AA′的中点.
同样地,点O也在线段BB′和CC′上,且OB=OB′,OC=OC′,即点O是BB′和CC′的中点.
因此,我们就得到
(1).关于中心对称的两个图形,对称点所连线段都经过对称中心,而且被对称中心所平分.
(2).关于中心对称的两个图形是全等图形.
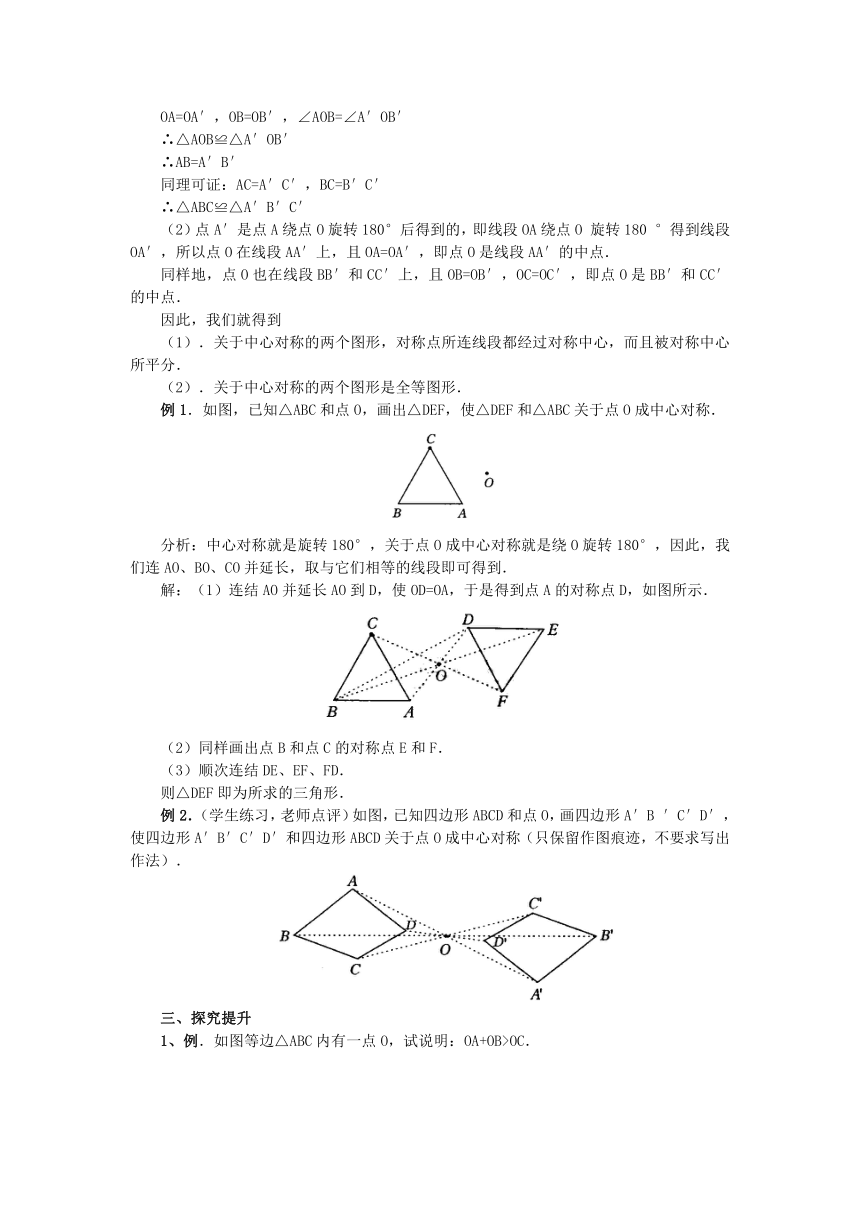
例1.如图,已知△ABC和点O,画出△DEF,使△DEF和△ABC关于点O成中心对称.
分析:中心对称就是旋转180°,关于点O成中心对称就是绕O旋转180°,因此,我们连AO、BO、CO并延长,取与它们相等的线段即可得到.
解:(1)连结AO并延长AO到D,使OD=OA,于是得到点A的对称点D,如图所示.
( http: / / www. )
(2)同样画出点B和点C的对称点E和F.
(3)顺次连结DE、EF、FD.
则△DEF即为所求的三角形.
例2.(学生练习,老师点评)如图,已知四边形ABCD和点O,画四边形A′B′C′D′,使四边形A′B′C′D′和四边形ABCD关于点O成中心对称(只保留作图痕迹,不要求写出作法).
三、探究提升
1、例.如图等边△ABC内有一点O,试说明:OA+OB>OC.
分析:要证明OA+OB>OC,必然把OA、OB、OC转为在一个三角形内,应用两边之和大于第三边(两点之间线段最短)来说明,因此要应用旋转.以A为旋转中心,旋转60°,便可把OA、OB、OC转化为一个三角形内.
解:如图,把△AOC以A为旋转中心顺时针方向旋转60°后,到△AO′B的位置,则△AOC≌△AO′B.
( http: / / www. )
∴AO=AO′,OC=O′B
又∵∠OAO′=60°,∴△AO′O为等边三角形.
∴AO=OO′
在△BOO′中,OO′+OB>BO′
即OA+OB>OC
2.如图,A、B、C是新建的三个居民小区,我们已经在到三个小区距离相等的地方修建了一所学校M,现计划修建居民小区D,其要求:(1)到学校的距离与其它小区到学校的距离相等;(2)控制人口密度,有利于生态环境建设,试写居民小区D的位置.
四、归纳小结(学生总结,老师点评)
本节课应掌握:
中心对称的两条基本性质:
1.关于中心对称的两个图形,对应点所连线都经过对称中心,而且被对称中心所平分;
2.关于中心对称的两个图形是全等图形及其它们的应用.
五、达标检测
一、选择题
1.下面图形中既是轴对称图形又是中心对称图形的是( )
A.直角 B.等边三角形 C.直角梯形 D.两条相交直线
2.下列命题中真命题是( )
A.两个等腰三角形一定全等
B.正多边形的每一个内角的度数随边数增多而减少
C.菱形既是中心对称图形,又是轴对称图形
D.两直线平行,同旁内角相等
3.将矩形ABCD沿AE折叠,得到如图的所示的图形,已知∠CED′=60°,则∠AED的大小是( )
A.60° B.50° C.75° D.55°
( http: / / www. )
二、填空题
1.关于中心对称的两个图形,对称点所连线段都经过__________,而且被对称中心所________.
2.关于中心对称的两个图形是_________图形.
3.线段既是轴对称图形又是中心对称图形,它的对称轴是_________,它的对称中心是__________.
教学反思:
本节课借助学生活动,比如:猜想、作图、观察、判断以及图片欣赏等方法是学生既能较好地理解本节的概念和性质,又能使学生在活动的过程中体验到生生合作、师生合作的愉悦和成功的喜悦。
第8周5课时
教学目标
(1) 理解关于中心对称的两个图形,对称点所连线段都经过对称中心,而且被对称中心所平分;理解关于中心对称的两个图形是全等图形;掌握这两个性质的运用.
(2)复习中心对称的基本概念(中心对称、对称中心,关于中心的对称点),提出问题,让学生分组讨论解决问题,老师引导总结中心对称的基本性质.
(3)培养学生的艺术创作能力和初步的艺术欣赏能力,培养勇于探索的精神,树立学习的自信心。
重难点、
1.重点:中心对称的两条基本性质及其运用.
2.难点与关键:让学生合作讨论,得出中心对称的两条基本性质.
教学方法:自学引导、当堂达标
教学过程
一、示标导学
1、复习引入
(老师口问,学生口答)
(1).什么叫中心对称?什么叫对称中心?
(2).什么叫关于中心的对称点?
(3).请同学随便画一三角形,以三角形一顶点为对称中心,画出这个三角形关于这个对称中心的对称图形,并分组讨论能得到什么结论.
(每组推荐一人上台陈述,老师点评)
2、出示学习目标(略)
二、自学释疑
1、结合学习目标和自学提纲自学课本 ,5分钟之后回答下列问题 ,在自学的过程中有问题的小组内讨论。
2、(老师)在黑板上画一个三角形ABC,分两种情况作两个图形
(1)作△ABC一顶点为对称中心的对称图形;
(2)作关于一定点O为对称中心的对称图形.
第一步,画出△ABC.
第二步,以△ABC的C点(或O点)为中心,旋转180°画出△A′B′和△A′B′C′,如图1和用2所示.
( http: / / www. )
(1) (2)
从图1中可以得出△ABC与△A′B′C是全等三角形;
分别连接对称点AA′、BB′、CC′,点O在这些线段上且O平分这些线段.
下面,我们就以图2为例来证明这两个结论.
证明:(1)在△ABC和△A′B′C′中,
OA=OA′,OB=OB′,∠AOB=∠A′OB′
∴△AOB≌△A′OB′
∴AB=A′B′
同理可证:AC=A′C′,BC=B′C′
∴△ABC≌△A′B′C′
(2)点A′是点A绕点O旋转180°后得到的,即线段OA绕点O旋转180°得到线段OA′,所以点O在线段AA′上,且OA=OA′,即点O是线段AA′的中点.
同样地,点O也在线段BB′和CC′上,且OB=OB′,OC=OC′,即点O是BB′和CC′的中点.
因此,我们就得到
(1).关于中心对称的两个图形,对称点所连线段都经过对称中心,而且被对称中心所平分.
(2).关于中心对称的两个图形是全等图形.
例1.如图,已知△ABC和点O,画出△DEF,使△DEF和△ABC关于点O成中心对称.
分析:中心对称就是旋转180°,关于点O成中心对称就是绕O旋转180°,因此,我们连AO、BO、CO并延长,取与它们相等的线段即可得到.
解:(1)连结AO并延长AO到D,使OD=OA,于是得到点A的对称点D,如图所示.
( http: / / www. )
(2)同样画出点B和点C的对称点E和F.
(3)顺次连结DE、EF、FD.
则△DEF即为所求的三角形.
例2.(学生练习,老师点评)如图,已知四边形ABCD和点O,画四边形A′B′C′D′,使四边形A′B′C′D′和四边形ABCD关于点O成中心对称(只保留作图痕迹,不要求写出作法).
三、探究提升
1、例.如图等边△ABC内有一点O,试说明:OA+OB>OC.
分析:要证明OA+OB>OC,必然把OA、OB、OC转为在一个三角形内,应用两边之和大于第三边(两点之间线段最短)来说明,因此要应用旋转.以A为旋转中心,旋转60°,便可把OA、OB、OC转化为一个三角形内.
解:如图,把△AOC以A为旋转中心顺时针方向旋转60°后,到△AO′B的位置,则△AOC≌△AO′B.
( http: / / www. )
∴AO=AO′,OC=O′B
又∵∠OAO′=60°,∴△AO′O为等边三角形.
∴AO=OO′
在△BOO′中,OO′+OB>BO′
即OA+OB>OC
2.如图,A、B、C是新建的三个居民小区,我们已经在到三个小区距离相等的地方修建了一所学校M,现计划修建居民小区D,其要求:(1)到学校的距离与其它小区到学校的距离相等;(2)控制人口密度,有利于生态环境建设,试写居民小区D的位置.
四、归纳小结(学生总结,老师点评)
本节课应掌握:
中心对称的两条基本性质:
1.关于中心对称的两个图形,对应点所连线都经过对称中心,而且被对称中心所平分;
2.关于中心对称的两个图形是全等图形及其它们的应用.
五、达标检测
一、选择题
1.下面图形中既是轴对称图形又是中心对称图形的是( )
A.直角 B.等边三角形 C.直角梯形 D.两条相交直线
2.下列命题中真命题是( )
A.两个等腰三角形一定全等
B.正多边形的每一个内角的度数随边数增多而减少
C.菱形既是中心对称图形,又是轴对称图形
D.两直线平行,同旁内角相等
3.将矩形ABCD沿AE折叠,得到如图的所示的图形,已知∠CED′=60°,则∠AED的大小是( )
A.60° B.50° C.75° D.55°
( http: / / www. )
二、填空题
1.关于中心对称的两个图形,对称点所连线段都经过__________,而且被对称中心所________.
2.关于中心对称的两个图形是_________图形.
3.线段既是轴对称图形又是中心对称图形,它的对称轴是_________,它的对称中心是__________.
教学反思:
本节课借助学生活动,比如:猜想、作图、观察、判断以及图片欣赏等方法是学生既能较好地理解本节的概念和性质,又能使学生在活动的过程中体验到生生合作、师生合作的愉悦和成功的喜悦。
同课章节目录
