2.5.1 第1课时 增长(降低)率问题 课件(共14张PPT)
文档属性
| 名称 | 2.5.1 第1课时 增长(降低)率问题 课件(共14张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 3.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-08 00:00:00 | ||
图片预览






文档简介
(共14张PPT)
2.5.1增长(降低)率问题
湘教版·九年级数学上册
上课课件
情景导入
列方程解应用问题的步骤是什么?
①审题
②设未知数
③列方程
④解方程
⑤答
一元二次方程模型在数学和实际生活中有着广泛的应用.
新课探究
某省农作物秸秆资源巨大,但合理使用量十分有限,因此该省准备引进适用的新技术来提高秸秆的合理使用率.若今年的使用率为40%,计划后年的使用率达到90%,求这两年秸杆使用率的年平均增长率(假定该省每年产生的秸秆总量不变).
若今年的使用率为40%,计划后年的使用率达到90%,求这两年秸杆使用率的年平均增长率(假定该省每年产生的秸秆总量不变).
若今年的使用率为40%,计划后年的使用率达到90%,求这两年秸杆使用率的年平均增长率(假定该省每年产生的秸秆总量不变).
解:
由于今年到后年间隔两年,所以问题中涉及的等量关系是:
今年的使用率×(1+年平均增长率)2=后年的使用率.
设这两年秸秆使用率的年平均增长率为x,则根据等量关系,可列出方程:
40%(
1
+x
)2
=90%.
整理,得
(
1+x
)2=2.25.
解:
由于今年到后年间隔两年,所以问题中涉及的等量关系是:
今年的使用率×(1+年平均增长率)2=后年的使用率.
设这两年秸秆使用率的年平均增长率为x,则根据等量关系,可列出方程:
40%(
1
+x
)2
=90%.
整理,得
(
1+x
)2=2.25.
解:
由于今年到后年间隔两年,所以问题中涉及的等量关系是:
今年的使用率×(1+年平均增长率)2=后年的使用率.
设这两年秸秆使用率的年平均增长率为x,则根据等量关系,可列出方程:
40%(
1
+x
)2
=90%.
整理,得
(
1+x
)2=2.25.
解得
x1=
0.5
=
50%,x2=
-2.5(不合题意,舍去).
因此,这两年秸杆使用率的年平均增长率为50%.
审
设
列
解
答
例1
为执行国家药品降价政策,给人民群众带来实惠,某药品经过两次降价,每瓶零售价由100元降为81元.求平均每次降价的百分率.
分析
问题中涉及的等量关系是:
原价×(1-平均每次降价的百分率)2=现行售价.
设平均每次降价的百分率为x,则根据等量关系得
100(
1-x)2=81.
整理,得
(
1-x
)2=0.81.
解得
x1=0.1=10%,x2=1.9(不合题意,舍去).
答:平均每次降价的百分率为10%.
解:
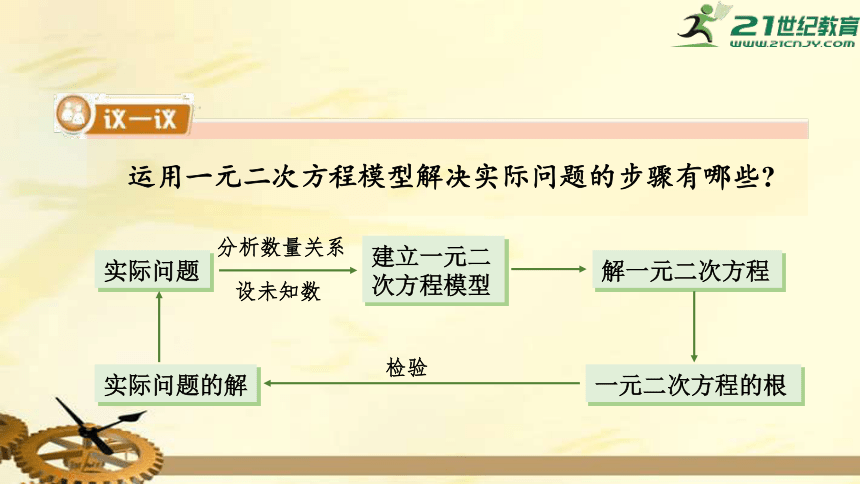
运用一元二次方程模型解决实际问题的步骤有哪些?
实际问题
建立一元二次方程模型
解一元二次方程
一元二次方程的根
实际问题的解
分析数量关系
设未知数
检验
课堂练习
练习
1.某校图书馆的藏书在两年内从5万册增加到7.2万册,问平均每年藏书增长的百分率是多少?
解:设平均每年藏书增长的百分率为x
则有
5(
1+x)2=7.2.
整理,得
(
1+x
)2=1.44.
解得
x1=0.2=20%,x2=-2.2(不合题意,舍去).
答:平均每年藏书增长的百分率是20%.
2.某小区2013年屋顶绿化面积为2000平方米,计划2015年屋顶绿化面积要达到2880平方米.如果每年屋顶绿化面积的增长率相同,那么这个增长率是多少?
解:设每年屋顶绿化面积的增长率为x
则有
2000(
1+x)2=2880.
整理,得
(
1+x
)2=1.44.
解得
x1=0.2=20%,x2=-2.2(不合题意,舍去).
答:每年屋顶绿化面积的增长率是20%.
3.某电脑公司2012年的各项经营收入中,经营电脑配件的收入为600万元,占全年经营总收入的40%,该公司预计2014年经营总收入要达到2160万元,且计划从2012年到2014年,每年经营总收入的年增长率相同,问2013年预计经营总收入为多少万元?
解:设每年经营总收入的年增长率为x
则有
600÷40%×(1+x)2=2160.
整理,得
(
1+x
)2=1.44.
解得
x1=0.2,x2=-2.2(不合题意,舍去).
∴每年经营总收入的年增长率为0.2
则2013年预计经营总收入为:
600÷40%×(1+0.2)=600÷40%×1.2=1800
答:2013年预计经营总收入为1800万元.
课堂小结
运用一元二次方程模型解决实际问题的步骤:
实际问题
建立一元二次方程模型
解一元二次方程
一元二次方程的根
实际问题的解
分析数量关系
设未知数
检验
1.从课后习题中选取;
2.完成练习册本课时的习题.
课后作业
谢谢观看
THANKS
谢谢大家!
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?欢迎加入21世纪教育网教师合作团队!!!月薪过万不是梦!!!
2.5.1增长(降低)率问题
湘教版·九年级数学上册
上课课件
情景导入
列方程解应用问题的步骤是什么?
①审题
②设未知数
③列方程
④解方程
⑤答
一元二次方程模型在数学和实际生活中有着广泛的应用.
新课探究
某省农作物秸秆资源巨大,但合理使用量十分有限,因此该省准备引进适用的新技术来提高秸秆的合理使用率.若今年的使用率为40%,计划后年的使用率达到90%,求这两年秸杆使用率的年平均增长率(假定该省每年产生的秸秆总量不变).
若今年的使用率为40%,计划后年的使用率达到90%,求这两年秸杆使用率的年平均增长率(假定该省每年产生的秸秆总量不变).
若今年的使用率为40%,计划后年的使用率达到90%,求这两年秸杆使用率的年平均增长率(假定该省每年产生的秸秆总量不变).
解:
由于今年到后年间隔两年,所以问题中涉及的等量关系是:
今年的使用率×(1+年平均增长率)2=后年的使用率.
设这两年秸秆使用率的年平均增长率为x,则根据等量关系,可列出方程:
40%(
1
+x
)2
=90%.
整理,得
(
1+x
)2=2.25.
解:
由于今年到后年间隔两年,所以问题中涉及的等量关系是:
今年的使用率×(1+年平均增长率)2=后年的使用率.
设这两年秸秆使用率的年平均增长率为x,则根据等量关系,可列出方程:
40%(
1
+x
)2
=90%.
整理,得
(
1+x
)2=2.25.
解:
由于今年到后年间隔两年,所以问题中涉及的等量关系是:
今年的使用率×(1+年平均增长率)2=后年的使用率.
设这两年秸秆使用率的年平均增长率为x,则根据等量关系,可列出方程:
40%(
1
+x
)2
=90%.
整理,得
(
1+x
)2=2.25.
解得
x1=
0.5
=
50%,x2=
-2.5(不合题意,舍去).
因此,这两年秸杆使用率的年平均增长率为50%.
审
设
列
解
答
例1
为执行国家药品降价政策,给人民群众带来实惠,某药品经过两次降价,每瓶零售价由100元降为81元.求平均每次降价的百分率.
分析
问题中涉及的等量关系是:
原价×(1-平均每次降价的百分率)2=现行售价.
设平均每次降价的百分率为x,则根据等量关系得
100(
1-x)2=81.
整理,得
(
1-x
)2=0.81.
解得
x1=0.1=10%,x2=1.9(不合题意,舍去).
答:平均每次降价的百分率为10%.
解:
运用一元二次方程模型解决实际问题的步骤有哪些?
实际问题
建立一元二次方程模型
解一元二次方程
一元二次方程的根
实际问题的解
分析数量关系
设未知数
检验
课堂练习
练习
1.某校图书馆的藏书在两年内从5万册增加到7.2万册,问平均每年藏书增长的百分率是多少?
解:设平均每年藏书增长的百分率为x
则有
5(
1+x)2=7.2.
整理,得
(
1+x
)2=1.44.
解得
x1=0.2=20%,x2=-2.2(不合题意,舍去).
答:平均每年藏书增长的百分率是20%.
2.某小区2013年屋顶绿化面积为2000平方米,计划2015年屋顶绿化面积要达到2880平方米.如果每年屋顶绿化面积的增长率相同,那么这个增长率是多少?
解:设每年屋顶绿化面积的增长率为x
则有
2000(
1+x)2=2880.
整理,得
(
1+x
)2=1.44.
解得
x1=0.2=20%,x2=-2.2(不合题意,舍去).
答:每年屋顶绿化面积的增长率是20%.
3.某电脑公司2012年的各项经营收入中,经营电脑配件的收入为600万元,占全年经营总收入的40%,该公司预计2014年经营总收入要达到2160万元,且计划从2012年到2014年,每年经营总收入的年增长率相同,问2013年预计经营总收入为多少万元?
解:设每年经营总收入的年增长率为x
则有
600÷40%×(1+x)2=2160.
整理,得
(
1+x
)2=1.44.
解得
x1=0.2,x2=-2.2(不合题意,舍去).
∴每年经营总收入的年增长率为0.2
则2013年预计经营总收入为:
600÷40%×(1+0.2)=600÷40%×1.2=1800
答:2013年预计经营总收入为1800万元.
课堂小结
运用一元二次方程模型解决实际问题的步骤:
实际问题
建立一元二次方程模型
解一元二次方程
一元二次方程的根
实际问题的解
分析数量关系
设未知数
检验
1.从课后习题中选取;
2.完成练习册本课时的习题.
课后作业
谢谢观看
THANKS
谢谢大家!
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?欢迎加入21世纪教育网教师合作团队!!!月薪过万不是梦!!!
同课章节目录
- 第1章 反比例函数
- 1.1 反比例函数
- 1.2 反比例函数的图像与性质
- 1.3 反比例函数的应用
- 第2章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程根的判别式
- 2.4 一元二次方程根与系数的关系
- 2.5 一元二次方程的应用
- 第3章 图形的相似
- 3.1 比例线段
- 3.2 平行线分线段成比例
- 3.3 相似图形
- 3.4 相似三角形的判定与性质
- 3.5 相似三角形的应用
- 3.6 位似
- 第4章 锐角三角函数
- 4.1 正弦和余弦
- 4.2 正切
- 4.3 解直角三角形
- 4.4 解直接三角形的应用
- 第5章 用样本推断总体
- 5.1 总体平均数与方差的估计
- 5.2 统计的简单应用
