2.5 一元二次方程的应用 习题课件(共20张PPT)
文档属性
| 名称 | 2.5 一元二次方程的应用 习题课件(共20张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-08 00:00:00 | ||
图片预览







文档简介
(共20张PPT)
习题
2.5
湘教版·九年级数学上册
习题课件
回顾总结
A
组
1.某市政府为落实保障性住房政策,去年已投入3亿元资金,并规划投入资金逐年增加,明年将投入12亿元资金用于保障性住房建设.求这两年中投入资金的年平均增长率.
【选自教材P53
习题2.5
第1题】
解:设这两年中投入资金的年平均增长率为x.
根据等量关系,可列出方程:
3(1+x)2=12
整理,得
(1+x)2=4
解得
x1=1,x2=-3(不符合题意,舍去)
答:这两年中投入资金的年平均增长率为100%.
2.某店只销售某种进价为40元/kg的特产.已知该店按60元/kg
出售时,平均每天可售出100
kg,后来经过市场调查发现,单价每降低1元,则平均每天的销售量可增加10
kg.若该店销售这种特产计划平均每天获利2240元.
【选自教材P53
习题2.5
第2题】
(1)每千克该种特产应降价多少元?
(2)为尽可能让利于顾客,则该店应按原售价的几折出售?
(1)每千克该种特产应降价多少元?
解:设每千克该种特产应降价x元.
根据等量关系得
(100+10x)(60-40-x)=2240.
整理,得x2-10x+24=0.
解得
x1=4,x2=6.
答:每千克该种特产应降价4元或6元.
(2)为尽可能让利于顾客,则该店应按原售价的几折出售?
解:根据题意得该种特产应降价6元,
即
答:为尽可能让利于顾客,则该店应按原售价的9折出售.
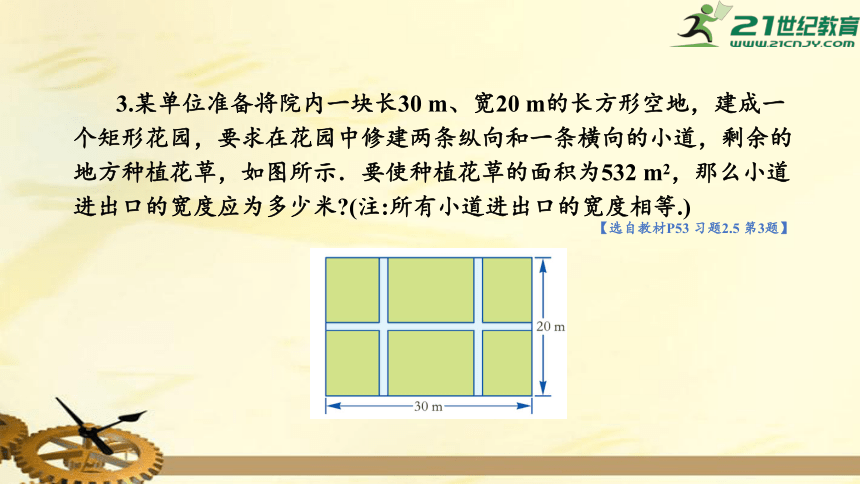
3.某单位准备将院内一块长30
m、宽20
m的长方形空地,建成一个矩形花园,要求在花园中修建两条纵向和一条横向的小道,剩余的地方种植花草,如图所示.要使种植花草的面积为532
m2,那么小道进出口的宽度应为多少米?(注:所有小道进出口的宽度相等.)
【选自教材P53
习题2.5
第3题】
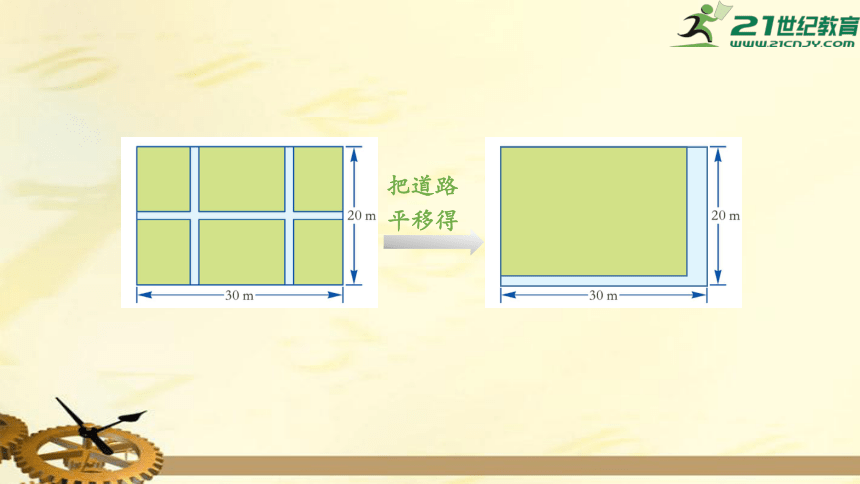
把道路平移得
则种植花草的矩形的长为(30-2x)m,宽为(20-x)m.
解:设小道进出口的宽度应为x米.
x
2x
根据等量关系得
(30-2x)(20-x)=532
整理,得x2-35x+34=0
解得
x1=1,x2=34(舍去)
答:小道进出口的宽度应为1m.
4.如图是某年8月的日历表,在此日历表上可以用一个矩形圈出3×3个位置相邻的9个数(如6,7,8,13,14,15,20,21,22).若圈出的9个数中,最大数与最小数的积为192,求这9个数的中的最大数.
【选自教材P53
习题2.5
第4题】
解:设圈出的数字中最大的为x,则最小数为x-16,
根据题意得
x(x-16)=192,
整理,得
x2-16x-192=0,
解得
x1=24,x2=-8(舍去)
答:这9个数中的最大数为24.
B
组
5.某旅行社在某地组织旅游团到北京旅游参观,每人的交通费、住宿费、门票费等费用共需3200元,如果把每人收费标准定为4600元,那么只有20人参加旅游团;高于4600元时,没有人参加;从4600元每降低100元,参加人数就增加10人.每人收费标准定为多少时,该旅行社从这个旅游团可获取利润64000元?
【选自教材P54
习题2.5
第5题】
解:设每人收费标准定为x元时,该旅行社从这个旅游团可获取利润64000元,则x<4600.
根据题意得
整理,得
解得
x2-8000x+16000000=0
x1=x2=4000
答:每人收费标准定为4000元时,该旅行社从这个旅游团可获取利润64000元.
6.(古代数学问题)
直田积八百六十四步,
只云长阔共六十步,
问长多阔几何.
——摘自古代数学家杨辉的《田亩比类乘除捷法》
意思是:一块矩形田地的面积为864平方步,只知道它的长与宽共60步,问它的长比宽多多少步?
一块矩形田地的面积为864平方步,只知道它的长与宽共60步,问它的长比宽多多少步?
解:设矩形田地的长为x步(x>30),则宽为(60-x)步.
根据题意得
x(60-x)=864,
整理,得
x2-60x+864=0,
解得
x1=36,x2=24(不合题意,舍去).
∴36-(60-36)=12(步).
答:它的长比宽多12步.
7.如图,在矩形ABCD中,BC=24
cm,P,Q,M,N分别从点A
,B,C,D同时出发,分别沿边AD,BC,CB,DA移动,且当有一个点先到达所在边的另一个端点时,其他各点也随之停止移动.已知移动一段时间后,若
BQ=x
cm(x≠0),则AP=2x
cm,CM
=
3x
cm,DN
=x2cm.
(1)当x为何值时,P,N两点重合?
(2)问Q,M两点能重合吗?若Q,M两点能重合,则求出相应的x的值;若Q,M两点不能重合,请说明理由.
(3)当x为何值时,以P,Q,M,N为顶点的四边形是平行四边形.
(1)当x为何值时,P,N两点重合?
x
2x
3x
x2
解:当点P与点N重合时,
则x?2?+2x=24,
解得x1?=4、x2?=-6(舍去),
所以当x=4时,P与N两点重合.
(2)问Q,M两点能重合吗?若Q,M两点能重合,则求出相应的x的值;若Q,M两点不能重合,请说明理由.
x
2x
3x
x2
解:当点Q与点M重合时,
由x+3x=24,解得x=6,
此时DN=x2?=36>24,不符合题意,
故点Q与点M不能重合.
(3)当x为何值时,以P,Q,M,N为顶点的四边形是平行四边形.
x
2x
3x
x2
解:由(1)知,点Q只能在点M的左侧
①当点P在点N的左侧时,
由24-(x+3x)=24-(2x+x2?),
解得x2?=2,x1=0(舍去);
所以当x=2时四边形PQMN是平行四边形;
②当点P在点N的右侧时,
则有24-(x+3x)=(2x+x2)-24,
解得
所以当
时四边形NQMP是平行四边形;
综上:当x=2或x=-3+
时,以P,Q,M,N为顶点的四边形是平行四边形.
x
2x
3x
x2
谢谢观看
THANKS
谢谢大家!
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?欢迎加入21世纪教育网教师合作团队!!!月薪过万不是梦!!!
习题
2.5
湘教版·九年级数学上册
习题课件
回顾总结
A
组
1.某市政府为落实保障性住房政策,去年已投入3亿元资金,并规划投入资金逐年增加,明年将投入12亿元资金用于保障性住房建设.求这两年中投入资金的年平均增长率.
【选自教材P53
习题2.5
第1题】
解:设这两年中投入资金的年平均增长率为x.
根据等量关系,可列出方程:
3(1+x)2=12
整理,得
(1+x)2=4
解得
x1=1,x2=-3(不符合题意,舍去)
答:这两年中投入资金的年平均增长率为100%.
2.某店只销售某种进价为40元/kg的特产.已知该店按60元/kg
出售时,平均每天可售出100
kg,后来经过市场调查发现,单价每降低1元,则平均每天的销售量可增加10
kg.若该店销售这种特产计划平均每天获利2240元.
【选自教材P53
习题2.5
第2题】
(1)每千克该种特产应降价多少元?
(2)为尽可能让利于顾客,则该店应按原售价的几折出售?
(1)每千克该种特产应降价多少元?
解:设每千克该种特产应降价x元.
根据等量关系得
(100+10x)(60-40-x)=2240.
整理,得x2-10x+24=0.
解得
x1=4,x2=6.
答:每千克该种特产应降价4元或6元.
(2)为尽可能让利于顾客,则该店应按原售价的几折出售?
解:根据题意得该种特产应降价6元,
即
答:为尽可能让利于顾客,则该店应按原售价的9折出售.
3.某单位准备将院内一块长30
m、宽20
m的长方形空地,建成一个矩形花园,要求在花园中修建两条纵向和一条横向的小道,剩余的地方种植花草,如图所示.要使种植花草的面积为532
m2,那么小道进出口的宽度应为多少米?(注:所有小道进出口的宽度相等.)
【选自教材P53
习题2.5
第3题】
把道路平移得
则种植花草的矩形的长为(30-2x)m,宽为(20-x)m.
解:设小道进出口的宽度应为x米.
x
2x
根据等量关系得
(30-2x)(20-x)=532
整理,得x2-35x+34=0
解得
x1=1,x2=34(舍去)
答:小道进出口的宽度应为1m.
4.如图是某年8月的日历表,在此日历表上可以用一个矩形圈出3×3个位置相邻的9个数(如6,7,8,13,14,15,20,21,22).若圈出的9个数中,最大数与最小数的积为192,求这9个数的中的最大数.
【选自教材P53
习题2.5
第4题】
解:设圈出的数字中最大的为x,则最小数为x-16,
根据题意得
x(x-16)=192,
整理,得
x2-16x-192=0,
解得
x1=24,x2=-8(舍去)
答:这9个数中的最大数为24.
B
组
5.某旅行社在某地组织旅游团到北京旅游参观,每人的交通费、住宿费、门票费等费用共需3200元,如果把每人收费标准定为4600元,那么只有20人参加旅游团;高于4600元时,没有人参加;从4600元每降低100元,参加人数就增加10人.每人收费标准定为多少时,该旅行社从这个旅游团可获取利润64000元?
【选自教材P54
习题2.5
第5题】
解:设每人收费标准定为x元时,该旅行社从这个旅游团可获取利润64000元,则x<4600.
根据题意得
整理,得
解得
x2-8000x+16000000=0
x1=x2=4000
答:每人收费标准定为4000元时,该旅行社从这个旅游团可获取利润64000元.
6.(古代数学问题)
直田积八百六十四步,
只云长阔共六十步,
问长多阔几何.
——摘自古代数学家杨辉的《田亩比类乘除捷法》
意思是:一块矩形田地的面积为864平方步,只知道它的长与宽共60步,问它的长比宽多多少步?
一块矩形田地的面积为864平方步,只知道它的长与宽共60步,问它的长比宽多多少步?
解:设矩形田地的长为x步(x>30),则宽为(60-x)步.
根据题意得
x(60-x)=864,
整理,得
x2-60x+864=0,
解得
x1=36,x2=24(不合题意,舍去).
∴36-(60-36)=12(步).
答:它的长比宽多12步.
7.如图,在矩形ABCD中,BC=24
cm,P,Q,M,N分别从点A
,B,C,D同时出发,分别沿边AD,BC,CB,DA移动,且当有一个点先到达所在边的另一个端点时,其他各点也随之停止移动.已知移动一段时间后,若
BQ=x
cm(x≠0),则AP=2x
cm,CM
=
3x
cm,DN
=x2cm.
(1)当x为何值时,P,N两点重合?
(2)问Q,M两点能重合吗?若Q,M两点能重合,则求出相应的x的值;若Q,M两点不能重合,请说明理由.
(3)当x为何值时,以P,Q,M,N为顶点的四边形是平行四边形.
(1)当x为何值时,P,N两点重合?
x
2x
3x
x2
解:当点P与点N重合时,
则x?2?+2x=24,
解得x1?=4、x2?=-6(舍去),
所以当x=4时,P与N两点重合.
(2)问Q,M两点能重合吗?若Q,M两点能重合,则求出相应的x的值;若Q,M两点不能重合,请说明理由.
x
2x
3x
x2
解:当点Q与点M重合时,
由x+3x=24,解得x=6,
此时DN=x2?=36>24,不符合题意,
故点Q与点M不能重合.
(3)当x为何值时,以P,Q,M,N为顶点的四边形是平行四边形.
x
2x
3x
x2
解:由(1)知,点Q只能在点M的左侧
①当点P在点N的左侧时,
由24-(x+3x)=24-(2x+x2?),
解得x2?=2,x1=0(舍去);
所以当x=2时四边形PQMN是平行四边形;
②当点P在点N的右侧时,
则有24-(x+3x)=(2x+x2)-24,
解得
所以当
时四边形NQMP是平行四边形;
综上:当x=2或x=-3+
时,以P,Q,M,N为顶点的四边形是平行四边形.
x
2x
3x
x2
谢谢观看
THANKS
谢谢大家!
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?欢迎加入21世纪教育网教师合作团队!!!月薪过万不是梦!!!
同课章节目录
- 第1章 反比例函数
- 1.1 反比例函数
- 1.2 反比例函数的图像与性质
- 1.3 反比例函数的应用
- 第2章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程根的判别式
- 2.4 一元二次方程根与系数的关系
- 2.5 一元二次方程的应用
- 第3章 图形的相似
- 3.1 比例线段
- 3.2 平行线分线段成比例
- 3.3 相似图形
- 3.4 相似三角形的判定与性质
- 3.5 相似三角形的应用
- 3.6 位似
- 第4章 锐角三角函数
- 4.1 正弦和余弦
- 4.2 正切
- 4.3 解直角三角形
- 4.4 解直接三角形的应用
- 第5章 用样本推断总体
- 5.1 总体平均数与方差的估计
- 5.2 统计的简单应用
