第二章 一元二次方程章末复习 上课课件(共54张PPT)
文档属性
| 名称 | 第二章 一元二次方程章末复习 上课课件(共54张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 3.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-08 00:00:00 | ||
图片预览









文档简介
(共54张PPT)
章末复习
湘教版·九年级数学上册
上课课件
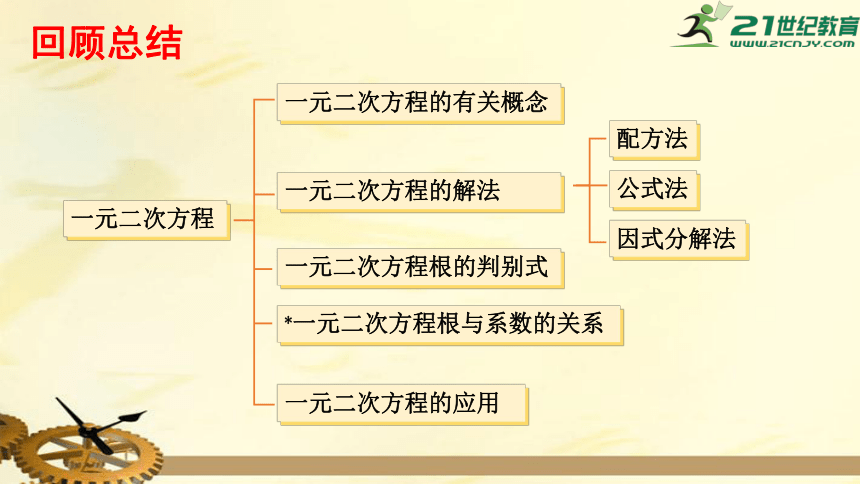
回顾总结
一元二次方程
一元二次方程的有关概念
一元二次方程的应用
一元二次方程的解法
一元二次方程根的判别式
一元二次方程根与系数的关系
配方法
公式法
因式分解法
如果一个方程通过整理可以使右边为0,而左边是只含有一个未知数的二次多项式,那么这样的方程叫作一元二次方程,它的一般形式是
ax2+bx
+c=0
(a,b,c是已知数,a≠0)
对于一元二次方程ax2+bx
+c=0
(a,b,c是已知数,a≠0)
,其中a,
b,c分别叫作二次项系数、一次项系数、常数项.
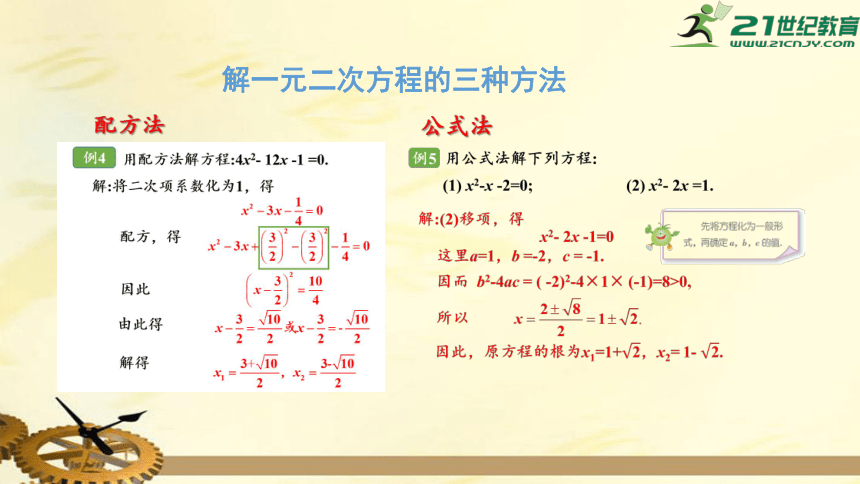
配方法
解一元二次方程的三种方法
公式法
因式分解法
一元二次方程ax2+
bx
+c
=0
(a≠0)的根的情况可由Δ
=
b2-
4ac来判断:
当Δ
>0时,原方程有两个不相等的实数根,其根为
当Δ
=0时,原方程有两个相等的实数根,其根为
当Δ
<0时,原方程没有实数根.
即
当Δ≥0时,一元二次方程的根与系数之间具有如下关系:
两根的和等于一次项系数与二次项系数的比的相反数,两根的积等于常数项与二次项系数的比.
韦达定理
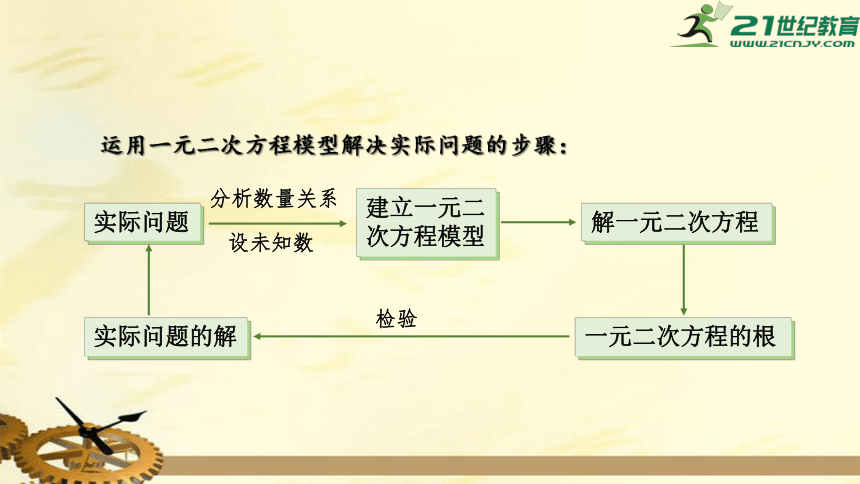
运用一元二次方程模型解决实际问题的步骤:
实际问题
建立一元二次方程模型
解一元二次方程
一元二次方程的根
实际问题的解
分析数量关系
设未知数
检验
课堂练习
A
组
1.把下列方程化为一元二次方程的一般形式,并指出其中的二次项系数、一次项系数和常数项.
(1)
5x2=
49;
(2)6x2-7x2
=3x
+5;
(3)
0.01t2-
3t=2t-
1;
(4)(2y-1
)
(
2y+5
)=6y
+4.
解:(1)原方程可化为
5x2-
49=0
所以该方程的二次项系数是5、一次项系数是0、常数项是-49.
课堂练习
A
组
1.把下列方程化为一元二次方程的一般形式,并指出其中的二次项系数、一次项系数和常数项.
(1)
5x2=
49;
(2)6x2-7x2
=3x
+5;
(3)
0.01t2-
3t=2t-
1;
(4)(2y-1
)
(
2y+5
)=6y
+4.
解:(2)原方程可化为
x2+3x
+5=0
所以该方程的二次项系数是1、一次项系数是3、常数项是5.
课堂练习
A
组
1.把下列方程化为一元二次方程的一般形式,并指出其中的二次项系数、一次项系数和常数项.
(1)
5x2=
49;
(2)6x2-7x2
=3x
+5;
(3)
0.01t2-
3t=2t-
1;
(4)(2y-1
)
(
2y+5
)=6y
+4.
解:(3)原方程可化为
0.01t2-
5t+
1=0
所以该方程的二次项系数是0.01、一次项系数是-5、常数项是1.
课堂练习
A
组
1.把下列方程化为一元二次方程的一般形式,并指出其中的二次项系数、一次项系数和常数项.
(1)
5x2=
49;
(2)6x2-7x2
=3x
+5;
(3)
0.01t2-
3t=2t-
1;
(4)(2y-1
)
(
2y+5
)=6y
+4.
解:(4)原方程可化为
4y2+2y-9=0
所以该方程的二次项系数是4、一次项系数是2、常数项是-9.
2.解下列方程:
(1)
49x2
-
144=0;
(2)
(
1-x)2=1;
(3)x2+8x
+16=0;
(4)
x
(7-x
)=4x2;
(5)
x(x-2)-3x2=0;
(6)x2-4x+4=64.
解:原方程可化为
根据平方根的意义,得
因此,原方程的根为
(1)
49x2
-
144=0;
解:根据平方根的意义,得
因此,原方程的根为
(2)(1-x)2=1
解:原方程可化为
根据平方根的意义,得
因此,原方程的根为
(3)x2+8x
+16=0;
解:原方程可化为
5x2-7x
=0.
把方程左边因式分解,得
x
(5x
-7)=0,
由此得
x=0或
5x
-7=0.
解得
x1=0
,x2
=
.
(4)
x
(7-x
)=4x2
解:原方程可化为
x2+x
=0.
把方程左边因式分解,得
x
(x
+1)=0,
由此得
x=0或
x
+1
=0.
解得
x1=0
,x2
=-1.
(5)
x(x-2)-3x2=0
(6)x2-4x+4=64
解:原方程可化为
(x-2)2=64.
根据平方根的意义,得
因此,原方程的根为
3.解下列方程:
(1)2x2-6x-
3=0;
(2)
x
(x
+5)=
24;
(3)
x
(x
+1)+2
(x-1)
=0;
(4)
(x-3)2+2x
(
x
-3
)=0;
(5)
3(x-2)2=x
(x-2).
解:这里a=2,b
=-6,c
=
-3.
因而
b2-4ac
=
(
-6)2-4×2×
(-3)=36+24=60>0,
因此,原方程的根为
.
所以
(1)2x2-6x-
3=0
(2)
x
(x
+5)=
24
解:原方程可化为
x2+5x
-24=0.
把方程左边因式分解,得
(x-3)
(x
+8)=0,
由此得
x-3=0或
x
+8
=0.
解得
x1=3
,x2
=-8.
(3)
x
(x
+1)+2
(x-1)
=0
解:原方程可化为
因而
b2-4ac
=
32-4×1×
(-2)=9+8=17>0,
因此,原方程的根为
.
所以
这里a=1,b
=3,c
=
-2.
x2+3x
-2=0.
(4)
(x-3)2+2x
(
x
-3
)=0
解:把方程左边因式分解,得
(x-3)
(x
-3+2x)=0,
由此得
x-3=0或
3x
-3
=0,
解得
x1=3
,x2
=1.
即
(x-3)
(3x
-3)=0
(5)
3(x-2)2=x
(x-2)
解:原方程可化为
3(x-2)2-x
(x-2)=0
把方程左边因式分解,得
(x-2)
[3(x
-2)-x]=0,
由此得
x-2=0或
2x
-6
=0.
解得
x1=2
,x2
=3.
即
(x-2)
(2x
-6)=0
4.不解方程,利用判别式判断下列方程的根的情况.
(1)
4x2+6x+9=0;
(2)
y2=y+5.
解:(1)因为Δ
=
b2-4ac
=62-4×4×9
=36+
144
=-108<0,
所以,原方程没有实数根.
解:(2)将原方程化为一般形式,得
y2-y-5=0
因为Δ
=b2-4ac
=
(
-1
)2-4×1×(-5)
=1+20=21>0,
所以,原方程有两个不相等的实数根.
(2)
y2=y+5
5.设x1,x2,是方程2x2-6x+3=0的两根,求下列各式的值:
(1)
x1+x2;
(2)x1x2;
(3)
x12+x22.
解:
6.若方程x2-3x
-1=0的两根为x1,x2,求
的值.
解:由韦达定理得
7.已知三个连续奇数的平方和是371,求这三个奇数.
解:设三个连续奇数中间的奇数为x.
由题意得
(x-2)2+x2+(x+2)2=371
整理,得
x2=121
解得
x1=11
,x2
=-11.
所以这三个奇数为9,11,13或-13,-11,-9.
8.北京奥运会的主会场“鸟巢”给世人留下了深刻的记忆.据了解,在鸟巢设计的最后阶段,经过了两次优化,鸟巢的结构用钢量从最初的54000
t减少到42000
t.求平均每次用钢量降低的百分率x(精确到1%).
解:根据等量关系得
54000(
1-x)2=42000.
整理,得
(
1-x
)2=
.
解得
(不合题意,舍去).
答:平均每次用钢量降低的百分率为12%.
∴
9.将一块长方形桌布铺在长为1.5
m、宽为1
m的长方形桌面上,各边下垂的长度相同,并且桌布的面积是桌面面积的2倍.求桌布下垂的长度.
解:设桌布下垂的长度为x
m,则根据等量关系得
(2x+1.5)(2x+1)=1.5×1×2
整理,得
8x2+10x-3=0,
解得
x1=0.25
,x2
=-1.5(不合题意,舍去).
答:桌布下垂的长度为0.25m,
10.如图为一张方格纸,纸上有一三角形(上色部分),其顶点均位于网格线的交点上.若上色部分的三角形面积为15.75
cm2,则此方格纸的面积为多少?
解:设每个小方格的边长为x
cm.
根据题意得
整理,得
x2=2.25
解得
x1=1.5
,x2
=-1.5(不合题意,舍去).
所以此方格纸的面积为4×1.5×4×1.5=36cm2.
11.现有一块矩形钢板ABCD,长AD=7.5
m,宽AB=5
m.在这块钢板上截除两个正方形得到如图所示的模具(阴影部分所示).已知
BE=
DF,且模具的面积等于原矩形钢板的面积的一半,求DF的长(精确到0.1
m).
7.5
m
5
m
x
m
x
m
解:设DF长为x
m.
∵DF+FC=DC=AB=5m,
∴PC=FC=(5-x)m.
∵BE+EP+PC=BC=AD=7.5m,
∴EP=2.5m.
依题意得
即
2x2-20x+25=0.
解得
,由于x2>5,因而舍去.
答:DF长约为1.5m.
12.如图,在
Rt
△ABC中,∠B=
90°,AC=
10
cm,BC=6
cm.现有两点P,Q分别从点A
和点C同时出发,沿边AB,CB向终点B移动.已知点P,Q的速度分别为2
cm/s,1
cm/s,且当其中一点到达终点时,另一点也随之停止移动.设P,Q两点移动时间为x
s.问是否存在这样的x,使得四边形APQC的面积等于16
cm2?若存在,请求出此时x的值;若不存在,请说明理由.
解:根据题意,得AP=2x
cm,CQ=x
cm,
假设存在这样的x,使得四边形APQC的面积等于16
cm2.
∵∠B=90°,AC=10,BC=6,
∴AB=8,BQ=(6-x)cm,BP=(8-2x)cm.
整理,得
x2-10x+16=0
解得
x1=2
,x2
=8.
但x2
=8时不合题意,因为P从A到B只需4s.
所以当x=2时,正好四边形APQC的面积等于16cm2.
B
组
13.解下列方程:
(1)(
3x+5
)2-6
(
3x+5
)+9=0;
(2)
x2+ax
-
2a2=0(a为常数).
解:把方程左边因式分解,得
[
(3x
+5)-3]2=0,
由此得
(3x
+5)-3=0,
解得
x1=x2
=
.
(1)(
3x+5
)2-6
(
3x+5
)+9=0;
解:把方程左边因式分解,得
(x
-a)(x+2a)=0,
由此得
x-a=0或
x
+2a
=0,
解得
x1=a,x2
=
-2a.
(2)
x2+ax
-
2a2=0(a为常数).
14.已知
a,b,c分别是△ABC的三边,其中a=1,c=4,且关于x的方程x2-4x
+b=0有两个相等的实数根,试判断△ABC的形状.
解:依题意得关于x的方程x2-4x
+b=0的判别式
Δ=b2-4ac=(-4)2-4×1×b=0
即
16-4b=0
∴b=4=c≠a.
∴
△ABC是等腰三角形.
15.设x1,x2是关于x的方程x2-4x+k+1=0的两个实数根.请问:是否存在实数k,使得x1·x2>x1+x2成立?试说明理由.
解:∵方程x2-4x+k+1=0有两个实数根,
∴
Δ
=16-4(k+1)≥0,
∴k≤3,
又x1·x2>x1+x2,
而x1+x2=4,x1·x2=k+1,
∴k+1>4,
所以不存在实数k,使得x1·x2>x1+x2成立.
即k>3,与k≤3矛盾
16.已知□ABCD的两邻边AB,AD的长是关于x的方程
的两个实数根.
(1)当m为何值时,□ABCD是菱形?求出这时菱形的边长;
(2)若AB的长为2,那么□ABCD的周长是多少?
解:∵平行四边形ABCD是菱形,
∴AB=AD,
∵AB、AD的长是关于x的一元二次方程
的两个实数根,
解得m=1,
(1)当m为何值时,□ABCD是菱形?求出这时菱形的边长;
关于x的一元二次方程为
∴当m为1时,平行四边形ABCD是菱形,且菱形的边长为
.
解:将x=2代入
中,
得
解得
∵AB、AD的长是关于x的一元二次方程
的两个实数根,
(2)若AB的长为2,那么□ABCD的周长是多少?
C
组
17.如图,一长方形地,长为x
m,宽为120
m,建筑商将它分为甲、乙、丙三个区域,甲、乙为正方形.现计划甲区域建筑住宅区,乙区域建筑商场,丙区域开辟为公园.若已知丙区域的面积为3200
m2,试求x的值.
3200
m2
解:依题意得甲区域的边长为120m,由图可知乙区域的边长为(x-120)m.
则丙区域的长为:(x-120)m
宽为:(240-x)m
根据等量关系得
(x-120)
(240-x)=3200
即x2-360x+32000=0
解得
x1=160
,x2
=200.
当x=160时,丙区域的长为x-120=160-120=40(m),宽为120-40=80(m),80>40,∴x=160不符合题意,舍去.
∴x=200.
18.有如下问题:“平面上,分别有2个点,3个点,4个点,5个点,…,n个点,其中任意3个点都不在一条直线上.经过每两点画一条直线,它们分别可以画多少条直线?”为了解决这一问题,小明设计了如下图表进行探究:
(1)请你帮小明在图表的横线上填上归纳出的一般性结论;
(2)若某人共画了171条直线,则该平面上共有多少个点?
(2)若某人共画了171条直线,则该平面上共有多少个点?
解:由
得
n2-n-342=0.
解得
n1=19
,n2
=-18(舍去).
所以平面上共有19个点.
谢谢观看
THANKS
谢谢大家!
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?欢迎加入21世纪教育网教师合作团队!!!月薪过万不是梦!!!
章末复习
湘教版·九年级数学上册
上课课件
回顾总结
一元二次方程
一元二次方程的有关概念
一元二次方程的应用
一元二次方程的解法
一元二次方程根的判别式
一元二次方程根与系数的关系
配方法
公式法
因式分解法
如果一个方程通过整理可以使右边为0,而左边是只含有一个未知数的二次多项式,那么这样的方程叫作一元二次方程,它的一般形式是
ax2+bx
+c=0
(a,b,c是已知数,a≠0)
对于一元二次方程ax2+bx
+c=0
(a,b,c是已知数,a≠0)
,其中a,
b,c分别叫作二次项系数、一次项系数、常数项.
配方法
解一元二次方程的三种方法
公式法
因式分解法
一元二次方程ax2+
bx
+c
=0
(a≠0)的根的情况可由Δ
=
b2-
4ac来判断:
当Δ
>0时,原方程有两个不相等的实数根,其根为
当Δ
=0时,原方程有两个相等的实数根,其根为
当Δ
<0时,原方程没有实数根.
即
当Δ≥0时,一元二次方程的根与系数之间具有如下关系:
两根的和等于一次项系数与二次项系数的比的相反数,两根的积等于常数项与二次项系数的比.
韦达定理
运用一元二次方程模型解决实际问题的步骤:
实际问题
建立一元二次方程模型
解一元二次方程
一元二次方程的根
实际问题的解
分析数量关系
设未知数
检验
课堂练习
A
组
1.把下列方程化为一元二次方程的一般形式,并指出其中的二次项系数、一次项系数和常数项.
(1)
5x2=
49;
(2)6x2-7x2
=3x
+5;
(3)
0.01t2-
3t=2t-
1;
(4)(2y-1
)
(
2y+5
)=6y
+4.
解:(1)原方程可化为
5x2-
49=0
所以该方程的二次项系数是5、一次项系数是0、常数项是-49.
课堂练习
A
组
1.把下列方程化为一元二次方程的一般形式,并指出其中的二次项系数、一次项系数和常数项.
(1)
5x2=
49;
(2)6x2-7x2
=3x
+5;
(3)
0.01t2-
3t=2t-
1;
(4)(2y-1
)
(
2y+5
)=6y
+4.
解:(2)原方程可化为
x2+3x
+5=0
所以该方程的二次项系数是1、一次项系数是3、常数项是5.
课堂练习
A
组
1.把下列方程化为一元二次方程的一般形式,并指出其中的二次项系数、一次项系数和常数项.
(1)
5x2=
49;
(2)6x2-7x2
=3x
+5;
(3)
0.01t2-
3t=2t-
1;
(4)(2y-1
)
(
2y+5
)=6y
+4.
解:(3)原方程可化为
0.01t2-
5t+
1=0
所以该方程的二次项系数是0.01、一次项系数是-5、常数项是1.
课堂练习
A
组
1.把下列方程化为一元二次方程的一般形式,并指出其中的二次项系数、一次项系数和常数项.
(1)
5x2=
49;
(2)6x2-7x2
=3x
+5;
(3)
0.01t2-
3t=2t-
1;
(4)(2y-1
)
(
2y+5
)=6y
+4.
解:(4)原方程可化为
4y2+2y-9=0
所以该方程的二次项系数是4、一次项系数是2、常数项是-9.
2.解下列方程:
(1)
49x2
-
144=0;
(2)
(
1-x)2=1;
(3)x2+8x
+16=0;
(4)
x
(7-x
)=4x2;
(5)
x(x-2)-3x2=0;
(6)x2-4x+4=64.
解:原方程可化为
根据平方根的意义,得
因此,原方程的根为
(1)
49x2
-
144=0;
解:根据平方根的意义,得
因此,原方程的根为
(2)(1-x)2=1
解:原方程可化为
根据平方根的意义,得
因此,原方程的根为
(3)x2+8x
+16=0;
解:原方程可化为
5x2-7x
=0.
把方程左边因式分解,得
x
(5x
-7)=0,
由此得
x=0或
5x
-7=0.
解得
x1=0
,x2
=
.
(4)
x
(7-x
)=4x2
解:原方程可化为
x2+x
=0.
把方程左边因式分解,得
x
(x
+1)=0,
由此得
x=0或
x
+1
=0.
解得
x1=0
,x2
=-1.
(5)
x(x-2)-3x2=0
(6)x2-4x+4=64
解:原方程可化为
(x-2)2=64.
根据平方根的意义,得
因此,原方程的根为
3.解下列方程:
(1)2x2-6x-
3=0;
(2)
x
(x
+5)=
24;
(3)
x
(x
+1)+2
(x-1)
=0;
(4)
(x-3)2+2x
(
x
-3
)=0;
(5)
3(x-2)2=x
(x-2).
解:这里a=2,b
=-6,c
=
-3.
因而
b2-4ac
=
(
-6)2-4×2×
(-3)=36+24=60>0,
因此,原方程的根为
.
所以
(1)2x2-6x-
3=0
(2)
x
(x
+5)=
24
解:原方程可化为
x2+5x
-24=0.
把方程左边因式分解,得
(x-3)
(x
+8)=0,
由此得
x-3=0或
x
+8
=0.
解得
x1=3
,x2
=-8.
(3)
x
(x
+1)+2
(x-1)
=0
解:原方程可化为
因而
b2-4ac
=
32-4×1×
(-2)=9+8=17>0,
因此,原方程的根为
.
所以
这里a=1,b
=3,c
=
-2.
x2+3x
-2=0.
(4)
(x-3)2+2x
(
x
-3
)=0
解:把方程左边因式分解,得
(x-3)
(x
-3+2x)=0,
由此得
x-3=0或
3x
-3
=0,
解得
x1=3
,x2
=1.
即
(x-3)
(3x
-3)=0
(5)
3(x-2)2=x
(x-2)
解:原方程可化为
3(x-2)2-x
(x-2)=0
把方程左边因式分解,得
(x-2)
[3(x
-2)-x]=0,
由此得
x-2=0或
2x
-6
=0.
解得
x1=2
,x2
=3.
即
(x-2)
(2x
-6)=0
4.不解方程,利用判别式判断下列方程的根的情况.
(1)
4x2+6x+9=0;
(2)
y2=y+5.
解:(1)因为Δ
=
b2-4ac
=62-4×4×9
=36+
144
=-108<0,
所以,原方程没有实数根.
解:(2)将原方程化为一般形式,得
y2-y-5=0
因为Δ
=b2-4ac
=
(
-1
)2-4×1×(-5)
=1+20=21>0,
所以,原方程有两个不相等的实数根.
(2)
y2=y+5
5.设x1,x2,是方程2x2-6x+3=0的两根,求下列各式的值:
(1)
x1+x2;
(2)x1x2;
(3)
x12+x22.
解:
6.若方程x2-3x
-1=0的两根为x1,x2,求
的值.
解:由韦达定理得
7.已知三个连续奇数的平方和是371,求这三个奇数.
解:设三个连续奇数中间的奇数为x.
由题意得
(x-2)2+x2+(x+2)2=371
整理,得
x2=121
解得
x1=11
,x2
=-11.
所以这三个奇数为9,11,13或-13,-11,-9.
8.北京奥运会的主会场“鸟巢”给世人留下了深刻的记忆.据了解,在鸟巢设计的最后阶段,经过了两次优化,鸟巢的结构用钢量从最初的54000
t减少到42000
t.求平均每次用钢量降低的百分率x(精确到1%).
解:根据等量关系得
54000(
1-x)2=42000.
整理,得
(
1-x
)2=
.
解得
(不合题意,舍去).
答:平均每次用钢量降低的百分率为12%.
∴
9.将一块长方形桌布铺在长为1.5
m、宽为1
m的长方形桌面上,各边下垂的长度相同,并且桌布的面积是桌面面积的2倍.求桌布下垂的长度.
解:设桌布下垂的长度为x
m,则根据等量关系得
(2x+1.5)(2x+1)=1.5×1×2
整理,得
8x2+10x-3=0,
解得
x1=0.25
,x2
=-1.5(不合题意,舍去).
答:桌布下垂的长度为0.25m,
10.如图为一张方格纸,纸上有一三角形(上色部分),其顶点均位于网格线的交点上.若上色部分的三角形面积为15.75
cm2,则此方格纸的面积为多少?
解:设每个小方格的边长为x
cm.
根据题意得
整理,得
x2=2.25
解得
x1=1.5
,x2
=-1.5(不合题意,舍去).
所以此方格纸的面积为4×1.5×4×1.5=36cm2.
11.现有一块矩形钢板ABCD,长AD=7.5
m,宽AB=5
m.在这块钢板上截除两个正方形得到如图所示的模具(阴影部分所示).已知
BE=
DF,且模具的面积等于原矩形钢板的面积的一半,求DF的长(精确到0.1
m).
7.5
m
5
m
x
m
x
m
解:设DF长为x
m.
∵DF+FC=DC=AB=5m,
∴PC=FC=(5-x)m.
∵BE+EP+PC=BC=AD=7.5m,
∴EP=2.5m.
依题意得
即
2x2-20x+25=0.
解得
,由于x2>5,因而舍去.
答:DF长约为1.5m.
12.如图,在
Rt
△ABC中,∠B=
90°,AC=
10
cm,BC=6
cm.现有两点P,Q分别从点A
和点C同时出发,沿边AB,CB向终点B移动.已知点P,Q的速度分别为2
cm/s,1
cm/s,且当其中一点到达终点时,另一点也随之停止移动.设P,Q两点移动时间为x
s.问是否存在这样的x,使得四边形APQC的面积等于16
cm2?若存在,请求出此时x的值;若不存在,请说明理由.
解:根据题意,得AP=2x
cm,CQ=x
cm,
假设存在这样的x,使得四边形APQC的面积等于16
cm2.
∵∠B=90°,AC=10,BC=6,
∴AB=8,BQ=(6-x)cm,BP=(8-2x)cm.
整理,得
x2-10x+16=0
解得
x1=2
,x2
=8.
但x2
=8时不合题意,因为P从A到B只需4s.
所以当x=2时,正好四边形APQC的面积等于16cm2.
B
组
13.解下列方程:
(1)(
3x+5
)2-6
(
3x+5
)+9=0;
(2)
x2+ax
-
2a2=0(a为常数).
解:把方程左边因式分解,得
[
(3x
+5)-3]2=0,
由此得
(3x
+5)-3=0,
解得
x1=x2
=
.
(1)(
3x+5
)2-6
(
3x+5
)+9=0;
解:把方程左边因式分解,得
(x
-a)(x+2a)=0,
由此得
x-a=0或
x
+2a
=0,
解得
x1=a,x2
=
-2a.
(2)
x2+ax
-
2a2=0(a为常数).
14.已知
a,b,c分别是△ABC的三边,其中a=1,c=4,且关于x的方程x2-4x
+b=0有两个相等的实数根,试判断△ABC的形状.
解:依题意得关于x的方程x2-4x
+b=0的判别式
Δ=b2-4ac=(-4)2-4×1×b=0
即
16-4b=0
∴b=4=c≠a.
∴
△ABC是等腰三角形.
15.设x1,x2是关于x的方程x2-4x+k+1=0的两个实数根.请问:是否存在实数k,使得x1·x2>x1+x2成立?试说明理由.
解:∵方程x2-4x+k+1=0有两个实数根,
∴
Δ
=16-4(k+1)≥0,
∴k≤3,
又x1·x2>x1+x2,
而x1+x2=4,x1·x2=k+1,
∴k+1>4,
所以不存在实数k,使得x1·x2>x1+x2成立.
即k>3,与k≤3矛盾
16.已知□ABCD的两邻边AB,AD的长是关于x的方程
的两个实数根.
(1)当m为何值时,□ABCD是菱形?求出这时菱形的边长;
(2)若AB的长为2,那么□ABCD的周长是多少?
解:∵平行四边形ABCD是菱形,
∴AB=AD,
∵AB、AD的长是关于x的一元二次方程
的两个实数根,
解得m=1,
(1)当m为何值时,□ABCD是菱形?求出这时菱形的边长;
关于x的一元二次方程为
∴当m为1时,平行四边形ABCD是菱形,且菱形的边长为
.
解:将x=2代入
中,
得
解得
∵AB、AD的长是关于x的一元二次方程
的两个实数根,
(2)若AB的长为2,那么□ABCD的周长是多少?
C
组
17.如图,一长方形地,长为x
m,宽为120
m,建筑商将它分为甲、乙、丙三个区域,甲、乙为正方形.现计划甲区域建筑住宅区,乙区域建筑商场,丙区域开辟为公园.若已知丙区域的面积为3200
m2,试求x的值.
3200
m2
解:依题意得甲区域的边长为120m,由图可知乙区域的边长为(x-120)m.
则丙区域的长为:(x-120)m
宽为:(240-x)m
根据等量关系得
(x-120)
(240-x)=3200
即x2-360x+32000=0
解得
x1=160
,x2
=200.
当x=160时,丙区域的长为x-120=160-120=40(m),宽为120-40=80(m),80>40,∴x=160不符合题意,舍去.
∴x=200.
18.有如下问题:“平面上,分别有2个点,3个点,4个点,5个点,…,n个点,其中任意3个点都不在一条直线上.经过每两点画一条直线,它们分别可以画多少条直线?”为了解决这一问题,小明设计了如下图表进行探究:
(1)请你帮小明在图表的横线上填上归纳出的一般性结论;
(2)若某人共画了171条直线,则该平面上共有多少个点?
(2)若某人共画了171条直线,则该平面上共有多少个点?
解:由
得
n2-n-342=0.
解得
n1=19
,n2
=-18(舍去).
所以平面上共有19个点.
谢谢观看
THANKS
谢谢大家!
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?欢迎加入21世纪教育网教师合作团队!!!月薪过万不是梦!!!
同课章节目录
- 第1章 反比例函数
- 1.1 反比例函数
- 1.2 反比例函数的图像与性质
- 1.3 反比例函数的应用
- 第2章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程根的判别式
- 2.4 一元二次方程根与系数的关系
- 2.5 一元二次方程的应用
- 第3章 图形的相似
- 3.1 比例线段
- 3.2 平行线分线段成比例
- 3.3 相似图形
- 3.4 相似三角形的判定与性质
- 3.5 相似三角形的应用
- 3.6 位似
- 第4章 锐角三角函数
- 4.1 正弦和余弦
- 4.2 正切
- 4.3 解直角三角形
- 4.4 解直接三角形的应用
- 第5章 用样本推断总体
- 5.1 总体平均数与方差的估计
- 5.2 统计的简单应用
