西师大版数学四年级上册 4.2三位数乘两位数 估算 课件(19张ppt)
文档属性
| 名称 | 西师大版数学四年级上册 4.2三位数乘两位数 估算 课件(19张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 西师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-07 00:00:00 | ||
图片预览





文档简介
三位数乘两位数的乘法
第2课时 估算
四
西师版数学四年级(上)
1.能结合现实情境进行估算,会进行三位数乘两位数的估算。
2.经历探究“单价、数量、总价”之间的数量关系的过程,初步渗透归纳思想。
3.感受估算在生活中的应用,体会数学来源于生活,又应用于生活。
学习目标
【重点】
掌握估算方法,能应用“单价×数量=总价”这个数量关系解决问题。
【难点】
能灵活选用估算方法。
课堂导入
看谁算得快!
1.实验小学今年有学生1501人,约是( )人。
2.小红家到学校有592米,约是( )米。
3.一台洗衣机售价是1096元,约是( )元。
4.新华书店又买来新书702本,约是( )本。
1500
600
1100
700
探究新知
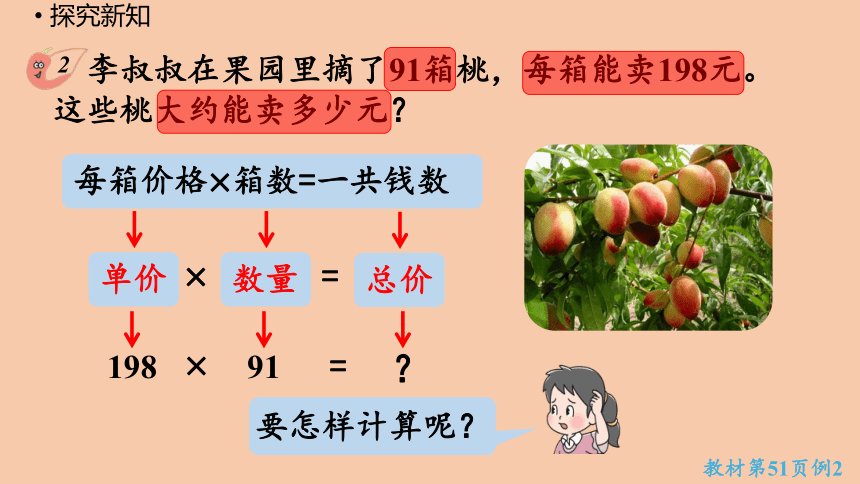
李叔叔在果园里摘了91箱桃,每箱能卖198元。这些桃大约能卖多少元?
每箱价格×箱数=一共钱数
单价
数量
总价
×
=
198
91
×
要怎样计算呢?
2
教材第51页例2
?
=
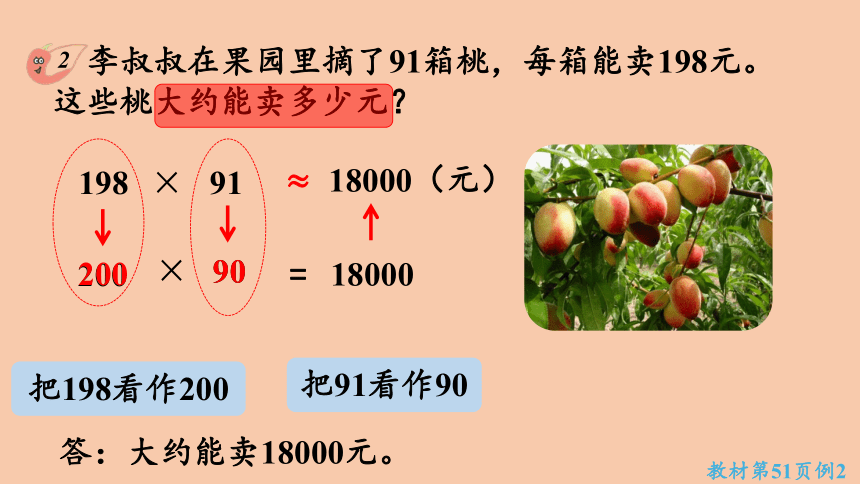
李叔叔在果园里摘了91箱桃,每箱能卖198元。这些桃大约能卖多少元?
198
91
=
200
90
18000
≈
18000
(元)
答:大约能卖18000元。
把198看作200
把91看作90
×
?
×
?
2
200
90
教材第51页例2
怎样进行估算?
应用“四舍五入”的方法取整十、整百的数或几百几十的数,方便估算。
当最低位的数是小于5的数时,应舍去。
当最低位的数是大于或等于5的数时,
应向前进一。
四舍
五入
四舍
五入
从上面的问题中,你知道什么是单价、数量、总价吗?
每箱能卖多少元是单价。
一共能卖多少元是总价。
卖了多少箱是数量。
单价、数量、总价之间有什么数量关系呢?
单价×数量=总价
单价=总价÷ 数量
数量=总价÷ 单价
四年级同学去秋游,每人需要49元(包括车票和门票),一共有104人参加,大约应该准备多少元买票?
每人需要49元
单价 × 数量 = 总价
一共有104人
估一估
?
四年级同学去秋游,每人需要49元(包括车票和门票),一共有104人参加,大约应该准备多少元买票?
估一估
49 × 104
=
50
100
×
5000
≈
5000
(元)
答:大约应该准备5000元买票。
把49看作50
把49看作50
课堂练习
47×53≈2000
69×51≈3000
1. 用估算的方法,检验下面各题,算的对吗?
39×713≈28000
308×58≈15000
×
×
√
×
50×50=2500
70×50=3500
40×700=28000
300×60=18000
检验:
检验:
检验:
检验:
2.全校制作校服大约需要多少元?
我们南郊小学有学生398人。
每人制作一套校服需要88元。
398 × 88
=
400
90
×
36000
≈
36000
(元)
答:全校制作校服大约需要36000元。
教材第54页练习十二第3题
3.刘宁走一步平均长度62厘米,他从教室径直走到花坛,一共走了252步。教室距花坛大约多少厘米?
252 × 62
=
250
60
×
15000
≈
15000
(厘米)
答:教室距花坛大约15000厘米。
4.填一填。
(1)果园每棵桃树每年施肥9 kg,202棵桃树每年大约需要施肥( )kg。
(2)一块长方形菜地长约798 m,宽约64 m,这块菜地面积大约( )m2。
(3)一个水果店平均每月营业收入为893元,一年大约收入( )元。
1800
9000
48000
9×202≈9×200=1800
798×64≈800×60=48000
893×12≈900×10=9000
5.判一判。
(1)超市有45台点读机,每台509元,估算时可以
把45看作50,509看作500,所以这些点读机大约
值2500元。 ( )
(2)口算30×900时,可以把900看作9个百,30看
作3个十,得27个千,就是27000。( )
×
√
50×500=25000
5.判一判。
(3)6?6×38≈24000,?可以填9。 ( )
(4)刘叔叔摘了198 kg草莓,如果每千克草莓9元,
刘叔叔大约可收入2000元,那么估算收入比实
际收入要多。 ( )
×
√
696×38
700
×
40
= 28000
≈
28000
这节课你有什么收获?
课堂小结
1.解决估算问题时,一般应用“四舍五入”的方法进行计算。
2.不能机械地套用“四舍五入”法,要具体问题具体分析,灵活运用所学知识。
课后作业
01
教材第51页“课堂活动”第3题。
作业课件中的相关练习。
02
第2课时 估算
四
西师版数学四年级(上)
1.能结合现实情境进行估算,会进行三位数乘两位数的估算。
2.经历探究“单价、数量、总价”之间的数量关系的过程,初步渗透归纳思想。
3.感受估算在生活中的应用,体会数学来源于生活,又应用于生活。
学习目标
【重点】
掌握估算方法,能应用“单价×数量=总价”这个数量关系解决问题。
【难点】
能灵活选用估算方法。
课堂导入
看谁算得快!
1.实验小学今年有学生1501人,约是( )人。
2.小红家到学校有592米,约是( )米。
3.一台洗衣机售价是1096元,约是( )元。
4.新华书店又买来新书702本,约是( )本。
1500
600
1100
700
探究新知
李叔叔在果园里摘了91箱桃,每箱能卖198元。这些桃大约能卖多少元?
每箱价格×箱数=一共钱数
单价
数量
总价
×
=
198
91
×
要怎样计算呢?
2
教材第51页例2
?
=
李叔叔在果园里摘了91箱桃,每箱能卖198元。这些桃大约能卖多少元?
198
91
=
200
90
18000
≈
18000
(元)
答:大约能卖18000元。
把198看作200
把91看作90
×
?
×
?
2
200
90
教材第51页例2
怎样进行估算?
应用“四舍五入”的方法取整十、整百的数或几百几十的数,方便估算。
当最低位的数是小于5的数时,应舍去。
当最低位的数是大于或等于5的数时,
应向前进一。
四舍
五入
四舍
五入
从上面的问题中,你知道什么是单价、数量、总价吗?
每箱能卖多少元是单价。
一共能卖多少元是总价。
卖了多少箱是数量。
单价、数量、总价之间有什么数量关系呢?
单价×数量=总价
单价=总价÷ 数量
数量=总价÷ 单价
四年级同学去秋游,每人需要49元(包括车票和门票),一共有104人参加,大约应该准备多少元买票?
每人需要49元
单价 × 数量 = 总价
一共有104人
估一估
?
四年级同学去秋游,每人需要49元(包括车票和门票),一共有104人参加,大约应该准备多少元买票?
估一估
49 × 104
=
50
100
×
5000
≈
5000
(元)
答:大约应该准备5000元买票。
把49看作50
把49看作50
课堂练习
47×53≈2000
69×51≈3000
1. 用估算的方法,检验下面各题,算的对吗?
39×713≈28000
308×58≈15000
×
×
√
×
50×50=2500
70×50=3500
40×700=28000
300×60=18000
检验:
检验:
检验:
检验:
2.全校制作校服大约需要多少元?
我们南郊小学有学生398人。
每人制作一套校服需要88元。
398 × 88
=
400
90
×
36000
≈
36000
(元)
答:全校制作校服大约需要36000元。
教材第54页练习十二第3题
3.刘宁走一步平均长度62厘米,他从教室径直走到花坛,一共走了252步。教室距花坛大约多少厘米?
252 × 62
=
250
60
×
15000
≈
15000
(厘米)
答:教室距花坛大约15000厘米。
4.填一填。
(1)果园每棵桃树每年施肥9 kg,202棵桃树每年大约需要施肥( )kg。
(2)一块长方形菜地长约798 m,宽约64 m,这块菜地面积大约( )m2。
(3)一个水果店平均每月营业收入为893元,一年大约收入( )元。
1800
9000
48000
9×202≈9×200=1800
798×64≈800×60=48000
893×12≈900×10=9000
5.判一判。
(1)超市有45台点读机,每台509元,估算时可以
把45看作50,509看作500,所以这些点读机大约
值2500元。 ( )
(2)口算30×900时,可以把900看作9个百,30看
作3个十,得27个千,就是27000。( )
×
√
50×500=25000
5.判一判。
(3)6?6×38≈24000,?可以填9。 ( )
(4)刘叔叔摘了198 kg草莓,如果每千克草莓9元,
刘叔叔大约可收入2000元,那么估算收入比实
际收入要多。 ( )
×
√
696×38
700
×
40
= 28000
≈
28000
这节课你有什么收获?
课堂小结
1.解决估算问题时,一般应用“四舍五入”的方法进行计算。
2.不能机械地套用“四舍五入”法,要具体问题具体分析,灵活运用所学知识。
课后作业
01
教材第51页“课堂活动”第3题。
作业课件中的相关练习。
02
