《运用平方差公式分解因式》课件
文档属性
| 名称 | 《运用平方差公式分解因式》课件 |

|
|
| 格式 | zip | ||
| 文件大小 | 6.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-04-25 00:00:00 | ||
图片预览





文档简介
(共20张PPT)
课题:运用平方差公式分解因式
作业问题反思
1、要按步骤分解;
2、公因式符号问题;
3、项数问题;
3m2a-12ma+3ma2
=3ma·m-3ma·4+3ma·a
=3ma(m-4+a)
–3ax2y+6x3yz
=-3x2y·a+3x2y·xz
=-3x2y(a-xz)
4x2-8ax+2x
=2x(2x-4a+1)
=2x·2x-2x·4a+2x·1
a
a
b
b
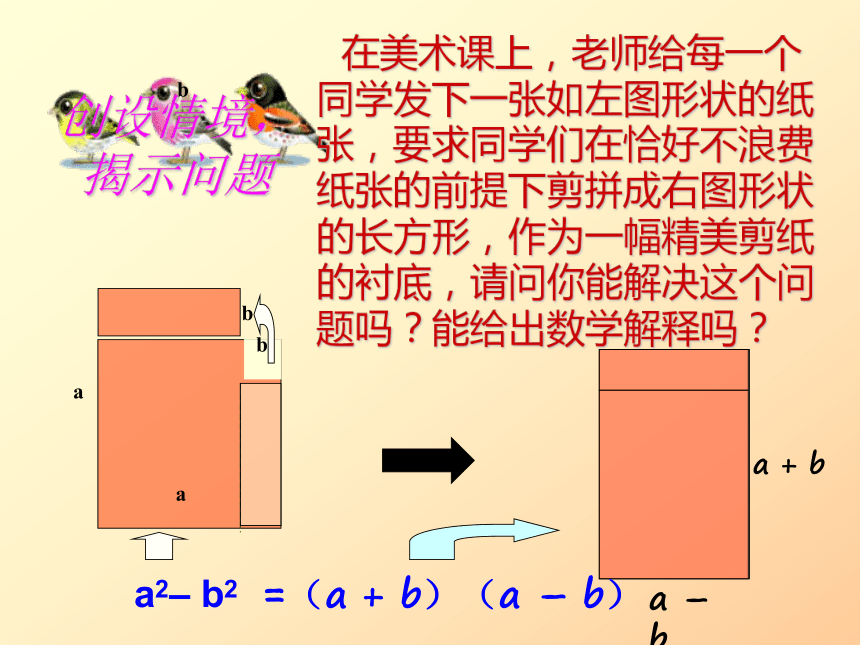
创设情境,
揭示问题
在美术课上,老师给每一个同学发下一张如左图形状的纸张,要求同学们在恰好不浪费纸张的前提下剪拼成右图形状的长方形,作为一幅精美剪纸的衬底,请问你能解决这个问题吗?能给出数学解释吗?
a – b
a + b
=(a + b)(a – b)
b
a2– b2
回顾与思考
=
a2-b2
(a+b) (a-b)
(a+b) (a-b)= a2-b2
两个数的平方差,等于这两个数的和与这两个数的差的积。
这两个数的和与这两个数的差的积,等于两个数的平方差。
请用语言叙述上面的表达式,
a - b = (a+b)(a-b)
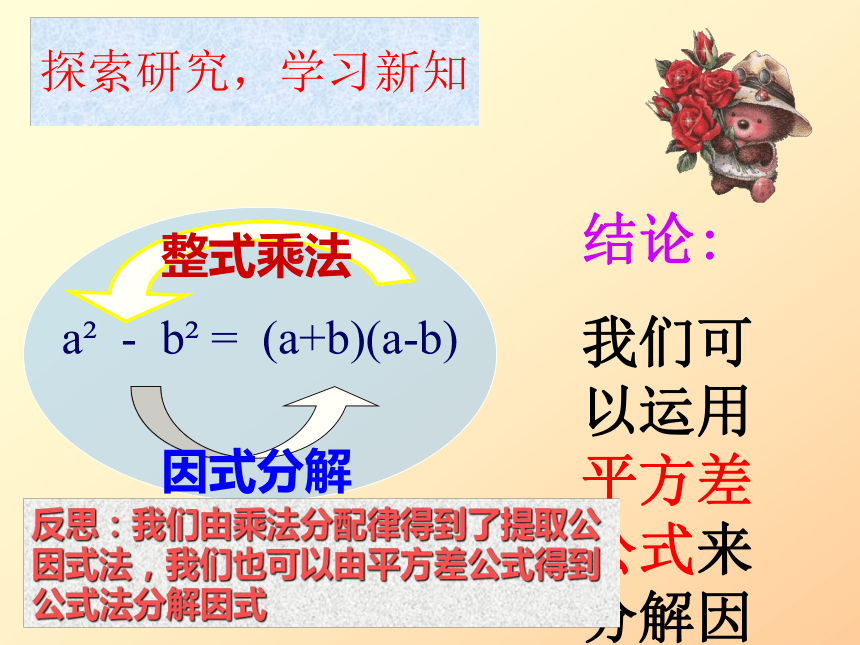
因式分解
整式乘法
结论:
我们可以运用平方差公式来分解因式
探索研究,学习新知
反思:我们由乘法分配律得到了提取公因式法,我们也可以由平方差公式得到公式法分解因式
1、条件:多项式是为二项式,每项可化为平方式,每项的底数看作一个数,多项式就为两数的平方差。
2、结论:是两个因式之积,每一个因式是一个二项式,即是两数和与两数差这积。
注意:只有符合平方差公式特征的代数式才能用平方差公式分解因式。!
a2 b2= (a+b)(a b)
认识平方差公式分解因式
特征:
理解应用 融会贯通
例题1、下列多项式能否用平方差公式分解因式?说说你的理由。
(1)4x2+y2 (2) 4x2-(-y)2
(3) -4x2-y2 (4) -4x2+y2
(5) a2-4 (6) a2+3
√
√
√
分析:能否用平方差公式分解因式,关键是能否找出两数,并能表达成两数的平方差!
(2x)2
2x
y
+
不能用平方差分解因式
-(4x2+y2)
不能
反思:能否用平方差公式分解因式的判断步骤是:1、各项能否写成平方项;2、确定出两数;3、确定两数平方是否相减;4、明确第一数和第二数。
a2-b2=(a + b)(a - b)
例题2:分解因式
16a2-1
=(4a)2-12
=(4a+1)(4a-1)
(1) 25x2-4
=(5x+2)(5x-2)
(2) 4x3 -x
=x(4x2-1)
=x(2x+1)(2x-1)
例题3:分解因式
反思:平方差公式分解因式步骤是1、写出平方数。2、比照公式代换两数。关键是找出两数。
想一想:是否有公因式,是否先用提取公因式法分解?试一下。
反思:先提公因式,再用公式法
(2) 4x3y - 9xy3
= xy(4x2-9y2)
=xy(2x+3y)(2x-3y)
例题4:分解因式
= (a2+9)(a2-9)
= (a2+9)(a+3) (a-3)
(1) a4 -81
是否还能继续分解?
反思:分解因式必须到不能继续分解为止
(2) 4a - 16b
(1) 4( a + b ) - 25( a -c )
=4 (a - 4b )
=(7a+2b-5c)(2b -3a+5c)
=[2(a+b)] -[5(a-c)]
=[2(a+b)+ 5(a-c)][2(a+b) - 5(a-c)]
= 4 (a+ 2b) (a- 2b)
例题5:分解因式
此题的两数是什么?
括号里是否可以化简?
反思:注意整体思想;注意括号里的化简。
练习反馈,拓展思维
把下列各式分解因式
(1) x - 1
(2) m - 9
(3) x - 4y
=(x+1)(x-1)
=(m+3)(m-3)
=(x+2y)(x-2y)
1、分解因式
4x2–y2=(4x+y)(4x-y )
诊断分析:
公式理解不准确,不能很好的把握公式中的项, 4x2–y2中4x2 相当于a2 ,则2x相当于“a”.
诊断
2、分解因式
x4–y4=(x2+y2)(x2–y2)
m5–m3=m3 (m2–1)
诊断分析:
综合运用提公因式,公式法公解因式时,提公因式后,另一个因式还可以继续分解,同学们千万要注意分解完毕后对结果进行检查,看是否分解彻底了。
下列多项式可以用平方差公式分解因式吗?如果可以进行分解因式。
① 4x2+y2
②-0.49x2+ y2
③ -4x2-y2
④ 9+(-y)2
公式中a、b可以是单独的数或字母,也可以是单项式或多项式。
25
1
如果一个多项式可以转化为a2-b2的形式,那么这个多项式就可以用平方差公式分解因式。
归纳总结 巩固新知
1.先提取公因式
2.再应用平方差公式分解
3.每个因式要化简,并且分解彻底
对于分解复杂的多项式,我们应该怎么做?
平方差公式:a2-b2 =(a+b)(a-b)
当公式中的a、b表示多项式时,要把这两个多项式看成两个整体,分解成的两个因式要进行去括号化简,若有同类项,要进行合并。
课后思考:
把一块纸板形状如图,请剪一个面积和这块纸板相等的长方形纸板,求出这个长方形纸板的长和宽,并画出图形。四人一组,合作讨论。
1.分解因式:
(1)4x3-x
( 2 ) a4-81
(3)(3x-4y)2-(4x+3y)2
(4)16(3m-2n)2-25(m-n)2
2、计算
(1)9992-9982
(2)25 × 2652-1352 × 25
课外书面作业
课题:运用平方差公式分解因式
作业问题反思
1、要按步骤分解;
2、公因式符号问题;
3、项数问题;
3m2a-12ma+3ma2
=3ma·m-3ma·4+3ma·a
=3ma(m-4+a)
–3ax2y+6x3yz
=-3x2y·a+3x2y·xz
=-3x2y(a-xz)
4x2-8ax+2x
=2x(2x-4a+1)
=2x·2x-2x·4a+2x·1
a
a
b
b
创设情境,
揭示问题
在美术课上,老师给每一个同学发下一张如左图形状的纸张,要求同学们在恰好不浪费纸张的前提下剪拼成右图形状的长方形,作为一幅精美剪纸的衬底,请问你能解决这个问题吗?能给出数学解释吗?
a – b
a + b
=(a + b)(a – b)
b
a2– b2
回顾与思考
=
a2-b2
(a+b) (a-b)
(a+b) (a-b)= a2-b2
两个数的平方差,等于这两个数的和与这两个数的差的积。
这两个数的和与这两个数的差的积,等于两个数的平方差。
请用语言叙述上面的表达式,
a - b = (a+b)(a-b)
因式分解
整式乘法
结论:
我们可以运用平方差公式来分解因式
探索研究,学习新知
反思:我们由乘法分配律得到了提取公因式法,我们也可以由平方差公式得到公式法分解因式
1、条件:多项式是为二项式,每项可化为平方式,每项的底数看作一个数,多项式就为两数的平方差。
2、结论:是两个因式之积,每一个因式是一个二项式,即是两数和与两数差这积。
注意:只有符合平方差公式特征的代数式才能用平方差公式分解因式。!
a2 b2= (a+b)(a b)
认识平方差公式分解因式
特征:
理解应用 融会贯通
例题1、下列多项式能否用平方差公式分解因式?说说你的理由。
(1)4x2+y2 (2) 4x2-(-y)2
(3) -4x2-y2 (4) -4x2+y2
(5) a2-4 (6) a2+3
√
√
√
分析:能否用平方差公式分解因式,关键是能否找出两数,并能表达成两数的平方差!
(2x)2
2x
y
+
不能用平方差分解因式
-(4x2+y2)
不能
反思:能否用平方差公式分解因式的判断步骤是:1、各项能否写成平方项;2、确定出两数;3、确定两数平方是否相减;4、明确第一数和第二数。
a2-b2=(a + b)(a - b)
例题2:分解因式
16a2-1
=(4a)2-12
=(4a+1)(4a-1)
(1) 25x2-4
=(5x+2)(5x-2)
(2) 4x3 -x
=x(4x2-1)
=x(2x+1)(2x-1)
例题3:分解因式
反思:平方差公式分解因式步骤是1、写出平方数。2、比照公式代换两数。关键是找出两数。
想一想:是否有公因式,是否先用提取公因式法分解?试一下。
反思:先提公因式,再用公式法
(2) 4x3y - 9xy3
= xy(4x2-9y2)
=xy(2x+3y)(2x-3y)
例题4:分解因式
= (a2+9)(a2-9)
= (a2+9)(a+3) (a-3)
(1) a4 -81
是否还能继续分解?
反思:分解因式必须到不能继续分解为止
(2) 4a - 16b
(1) 4( a + b ) - 25( a -c )
=4 (a - 4b )
=(7a+2b-5c)(2b -3a+5c)
=[2(a+b)] -[5(a-c)]
=[2(a+b)+ 5(a-c)][2(a+b) - 5(a-c)]
= 4 (a+ 2b) (a- 2b)
例题5:分解因式
此题的两数是什么?
括号里是否可以化简?
反思:注意整体思想;注意括号里的化简。
练习反馈,拓展思维
把下列各式分解因式
(1) x - 1
(2) m - 9
(3) x - 4y
=(x+1)(x-1)
=(m+3)(m-3)
=(x+2y)(x-2y)
1、分解因式
4x2–y2=(4x+y)(4x-y )
诊断分析:
公式理解不准确,不能很好的把握公式中的项, 4x2–y2中4x2 相当于a2 ,则2x相当于“a”.
诊断
2、分解因式
x4–y4=(x2+y2)(x2–y2)
m5–m3=m3 (m2–1)
诊断分析:
综合运用提公因式,公式法公解因式时,提公因式后,另一个因式还可以继续分解,同学们千万要注意分解完毕后对结果进行检查,看是否分解彻底了。
下列多项式可以用平方差公式分解因式吗?如果可以进行分解因式。
① 4x2+y2
②-0.49x2+ y2
③ -4x2-y2
④ 9+(-y)2
公式中a、b可以是单独的数或字母,也可以是单项式或多项式。
25
1
如果一个多项式可以转化为a2-b2的形式,那么这个多项式就可以用平方差公式分解因式。
归纳总结 巩固新知
1.先提取公因式
2.再应用平方差公式分解
3.每个因式要化简,并且分解彻底
对于分解复杂的多项式,我们应该怎么做?
平方差公式:a2-b2 =(a+b)(a-b)
当公式中的a、b表示多项式时,要把这两个多项式看成两个整体,分解成的两个因式要进行去括号化简,若有同类项,要进行合并。
课后思考:
把一块纸板形状如图,请剪一个面积和这块纸板相等的长方形纸板,求出这个长方形纸板的长和宽,并画出图形。四人一组,合作讨论。
1.分解因式:
(1)4x3-x
( 2 ) a4-81
(3)(3x-4y)2-(4x+3y)2
(4)16(3m-2n)2-25(m-n)2
2、计算
(1)9992-9982
(2)25 × 2652-1352 × 25
课外书面作业
