29.3 课题学习 制作立体模型-2020-2021学年人教版九年级数学下册练习(Word版 含答案)
文档属性
| 名称 | 29.3 课题学习 制作立体模型-2020-2021学年人教版九年级数学下册练习(Word版 含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 213.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-07 00:00:00 | ||
图片预览

文档简介
课题学习制作立体模型练习
一、选择题
分别观察下列几何体,其中主视图、左视图和俯视图完全相同的是(????)
A. 圆锥 B. 圆柱
C. 三棱柱 D. 正方体
如图分别是某校体育运动会的颁奖台和它的主视图,则其左视图是(????)
A.
B.
C.
D.
某几何体的三视图如图,则该几何体是(????)
A. 长方体
B. 圆柱
C. 球
D. 正三棱柱
如图是某个几何体的三视图,则该几何体是(????)
A. 圆锥
B. 长方体
C. 三棱柱
D. 圆柱
一个几何体的三视图如图所示,则这个几何体是(????)
A.
B.
C.
D.
如图是由几个相同大小的小正方体搭建而成的几何体的主视图和俯视图,则搭建这个几何体所需要的小正方体的个数至少为(????)
A. 5 B. 6 C. 7 D. 8
如图(1)(2)是放置一个水管三叉接头,若从正面看这个接头时,看到图形如图(2)所示,则从上面看这个接头时,看到的图形是(????)
A. B. C. D.
如图是由几个小立方块所搭成的几何体的俯视图,小正方形中的数字表示在该位置小立方块的个数,则这个几何体的左视图为(????)
A. B.
C. D.
某几何体的俯视图如图所示,图中数字表示该位置上的小正方体的个数,则这个几何体的主视图是(????)
A. B. C. D.
某立体图形的三视图如图所示,则该立体图形的名称是(????)
A. 正方体
B. 长方体
C. 圆柱体
D. 圆锥体
如图,是由一些棱长为1cm的小正方体构成的立体图形的三种视图,那么这个立体图形的体积是(????)
A. 3cm3
B. 14cm3
C. 5cm3
D. 7cm3
如图是一个几体何的三视图(图中尺寸单位:cm),则这个几何体侧面积为
A. 48π?cm2 B. 24π?cm2 C. 12π?cm2 D. 9π?cm2
二、填空题
一个几何体由若干个大小相同的小正方体组成,从正面和从上面看到的形状图如图所示,则这个几何体中小正方体的个数最多是______.
如图是一个几何体的三视图,则这个几何体的侧面积是______cm2.
如图所示,是从不同方向看到的由一些小立方块搭成的几何体的形状图,若在所搭几何体的基础上(不改变原几何体中小立方块的位置),继续添加相同的小立方块,以便搭成一个大正方体,则至少还需要______个小立方块.
根据几何体的主视图和俯视图,搭成该几何体的小正方体最多___________个.
一个侧面积为162πcm2的圆锥,其主视图为等腰直角三角形,则这个圆锥的高为____cm.
三、解答题
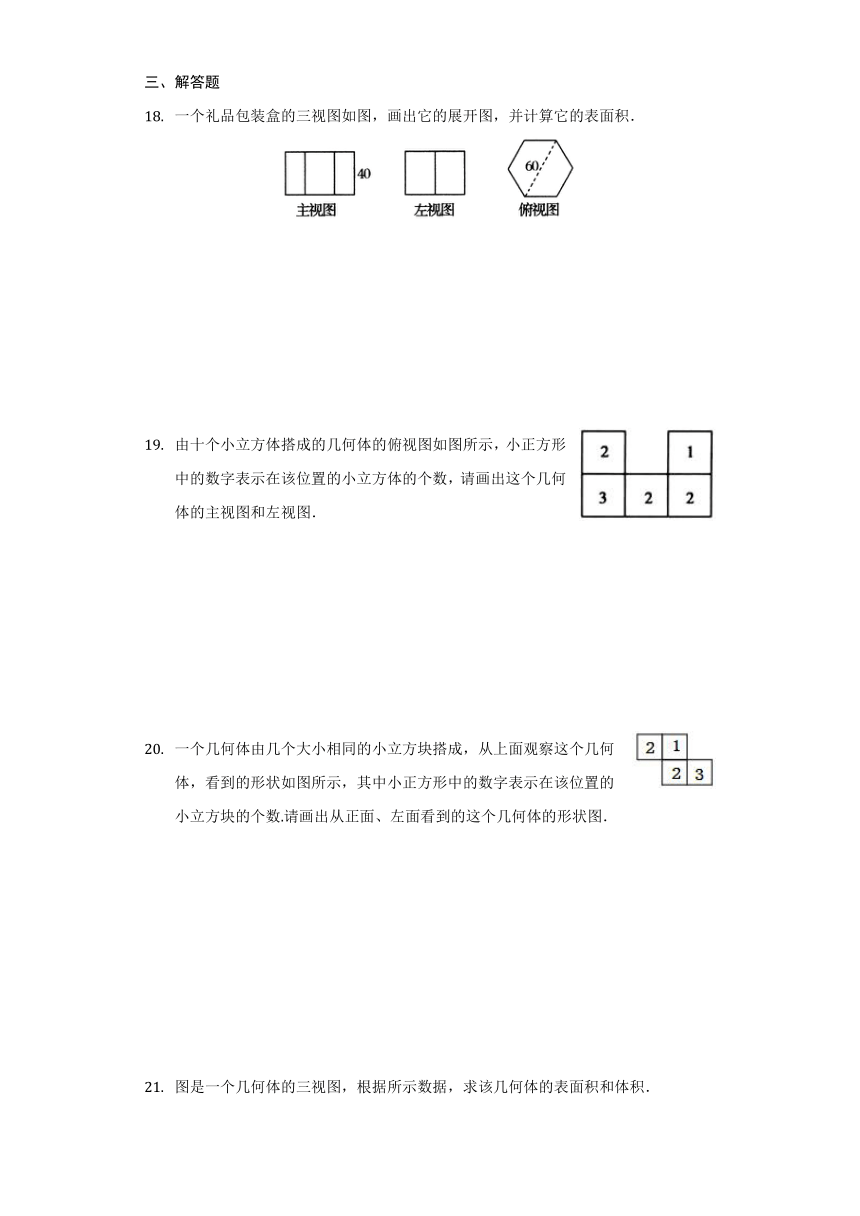
一个礼品包装盒的三视图如图,画出它的展开图,并计算它的表面积.
由十个小立方体搭成的几何体的俯视图如图所示,小正方形中的数字表示在该位置的小立方体的个数,请画出这个几何体的主视图和左视图.
一个几何体由几个大小相同的小立方块搭成,从上面观察这个几何体,看到的形状如图所示,其中小正方形中的数字表示在该位置的小立方块的个数.请画出从正面、左面看到的这个几何体的形状图.
图是一个几何体的三视图,根据所示数据,求该几何体的表面积和体积.
答案和解析
1.【答案】D
【解析】解:圆锥的主视图、左视图都是等腰三角形,而俯视图是圆,因此选项A不符合题意;
圆柱体的主视图、左视图都是矩形,而俯视图是圆形,因此选项B不符合题意;
三棱柱主视图、左视图都是矩形,而俯视图是三角形,因此选项C不符合题意;
正方体的三视图都是形状、大小相同的正方形,因此选项D符合题意;
2.【答案】D
【解析】解:从左边看是一个矩形被分为3部分,上面的分线是实线,下面的分线是虚线.
3.【答案】B
【解析】解:根据主视图和俯视图为长方形可得此几何体为柱体,左视图为圆可得此几何体为圆柱,
4.【答案】D
【解析】解:根据主视图和左视图为矩形判断出是柱体,根据俯视图是圆可判断出这个几何体是圆柱.
5.【答案】D
【解答】
解:根据主视图和左视图为矩形判断出是柱体,根据俯视图是三角形可判断出这个几何体应该是三棱柱.
6.【答案】B
【解析】解:综合主视图和俯视图,底层最少有4个小立方体,第二层最少有2个小立方体,因此搭成这个几何体的小正方体的个数最少是6个.
7.【答案】A
【解析】解:从上面看,可得到左边是一个圆,右边是长方形,一组对边与圆相接;
8.【答案】D
【解析】解:左视图是从左边看到的平面图形,发现从左面看一共有两列,左边一列有2个正方形,右边一列有3个正方形,
9.【答案】B
【解答】解:从正面看去,一共两列,左边有2竖列,右边是1竖列.
故选:B.
10.【答案】C
【解析】解:俯视图是圆形,说明这个几何体的上下有两个面是圆形的,左视图、左视图都是长方形的,于是可以判断这个几何体是圆柱体.
11.【答案】A
【解析】解:易得第一层有2个小正方体,第二层有1个小正方体,一共有3个,
这个几何体的体积为3cm3
12.【答案】B
【解答】
解:由三视图得这个几何体为圆锥,圆锥的母线长为8,底面圆的直径为6,
所以这个几何体的侧面积=12×π×6×8=24π(cm2).
13.【答案】5
【解析】解:根据主视图、左视图可知,其俯视图最多为2×2的正方形,如图所示,
其中数字表示该位置最多能摆放的小立方体的个数,
所以,这个几何体中小正方体的个数最多是5个,
14.【答案】(36+83)
【解析】解:观察三视图知:该几何体为三棱柱,高为3cm,长为4cm,
侧面积为:3×4×3+2×12×4×23=(36+83)cm2.
则这个几何体的侧面积是(36+83)cm2.
15.【答案】19
【解答】
解:由主视图可知,原来的几何体由三层,且有3列,
由左视图可知,搭成的几何体共有3行,
由俯视图易得最底层有5个小立方体,第二层有2个小立方体,第三层有1个小立方体,那么共有5+2+1=8个几何体组成.
若搭成一个大正方体,共需3×3×3=27个小立方体,
所以至少还需27?8=19个小立方体,
故答案为19.
16.【答案】7
【解答】
解:根据题意得:
则搭成该几何体的小正方体最多是1+1+1+2+2=7(个).
故答案为7.
17.【答案】4
【解析】解:设底面半径为r,母线为l,
∵主视图为等腰直角三角形,
∴2r=2l,
∴侧面积S侧=πrl=2πr2=162πcm2,
解得?r=4,l=42,
∴圆锥的高?=4cm,
18.【答案】解:该包装盒的几何形状是直六棱柱,画出的平面展开图如下:
过俯视图的一边AB作正六边形对角线EF的垂线BC、AD,
设CE=x,
因为六边形是正六边形,
所以正六边形的一个内角为120°,
所以∠BEC=60°,故∠EBC=30°,
所以BE=2CE=2x,DF=x,
所以DC=60?2x,
根据正六边形的性质可得AB=BE=2x,由作图步骤可得CD=AB,
所以60?2x=2x,
解得x=15,故2x=30
所以正六边形的边长为30.
所以正六棱柱的侧面为长为40,宽为30的长方形,上下底面是边长为30的正六边形,
将正六边形可以分割为6个边长为30的等边三角形.
∵每个等边三角形的边长为30,
∴每个等边三角形的面积为12×30×30×sin60?=450×32=2253,
∴该包装盒的底面的面积为12×2253=27003.
∵该包装盒的侧面是6个长为40,宽为30的长方形,
∴该包装盒的侧面的面积为6×40×30=7200,
∴该包装盒的表面积为27003+7200.
19.【答案】解:根据题意,这个几何体的主视图和左视图如下图所示:
20.【答案】解:如图所示:
21.【答案】解:由题意可知:该几何体的上面是底面直径为20cm,高为32cm的圆柱,下面是长为30cm,宽为25cm,高为40cm的长方体,
∴表面积为:30×25×2+30×40×2+25×40×2+π×20×32=5900+640π(cm2)
体积为:
30×25×40+π×(20÷2)2×32=30000+3200π(cm3)
答:该几何体的表面积(5900+640π)cm2和体积为(30000+3200π)cm3.
一、选择题
分别观察下列几何体,其中主视图、左视图和俯视图完全相同的是(????)
A. 圆锥 B. 圆柱
C. 三棱柱 D. 正方体
如图分别是某校体育运动会的颁奖台和它的主视图,则其左视图是(????)
A.
B.
C.
D.
某几何体的三视图如图,则该几何体是(????)
A. 长方体
B. 圆柱
C. 球
D. 正三棱柱
如图是某个几何体的三视图,则该几何体是(????)
A. 圆锥
B. 长方体
C. 三棱柱
D. 圆柱
一个几何体的三视图如图所示,则这个几何体是(????)
A.
B.
C.
D.
如图是由几个相同大小的小正方体搭建而成的几何体的主视图和俯视图,则搭建这个几何体所需要的小正方体的个数至少为(????)
A. 5 B. 6 C. 7 D. 8
如图(1)(2)是放置一个水管三叉接头,若从正面看这个接头时,看到图形如图(2)所示,则从上面看这个接头时,看到的图形是(????)
A. B. C. D.
如图是由几个小立方块所搭成的几何体的俯视图,小正方形中的数字表示在该位置小立方块的个数,则这个几何体的左视图为(????)
A. B.
C. D.
某几何体的俯视图如图所示,图中数字表示该位置上的小正方体的个数,则这个几何体的主视图是(????)
A. B. C. D.
某立体图形的三视图如图所示,则该立体图形的名称是(????)
A. 正方体
B. 长方体
C. 圆柱体
D. 圆锥体
如图,是由一些棱长为1cm的小正方体构成的立体图形的三种视图,那么这个立体图形的体积是(????)
A. 3cm3
B. 14cm3
C. 5cm3
D. 7cm3
如图是一个几体何的三视图(图中尺寸单位:cm),则这个几何体侧面积为
A. 48π?cm2 B. 24π?cm2 C. 12π?cm2 D. 9π?cm2
二、填空题
一个几何体由若干个大小相同的小正方体组成,从正面和从上面看到的形状图如图所示,则这个几何体中小正方体的个数最多是______.
如图是一个几何体的三视图,则这个几何体的侧面积是______cm2.
如图所示,是从不同方向看到的由一些小立方块搭成的几何体的形状图,若在所搭几何体的基础上(不改变原几何体中小立方块的位置),继续添加相同的小立方块,以便搭成一个大正方体,则至少还需要______个小立方块.
根据几何体的主视图和俯视图,搭成该几何体的小正方体最多___________个.
一个侧面积为162πcm2的圆锥,其主视图为等腰直角三角形,则这个圆锥的高为____cm.
三、解答题
一个礼品包装盒的三视图如图,画出它的展开图,并计算它的表面积.
由十个小立方体搭成的几何体的俯视图如图所示,小正方形中的数字表示在该位置的小立方体的个数,请画出这个几何体的主视图和左视图.
一个几何体由几个大小相同的小立方块搭成,从上面观察这个几何体,看到的形状如图所示,其中小正方形中的数字表示在该位置的小立方块的个数.请画出从正面、左面看到的这个几何体的形状图.
图是一个几何体的三视图,根据所示数据,求该几何体的表面积和体积.
答案和解析
1.【答案】D
【解析】解:圆锥的主视图、左视图都是等腰三角形,而俯视图是圆,因此选项A不符合题意;
圆柱体的主视图、左视图都是矩形,而俯视图是圆形,因此选项B不符合题意;
三棱柱主视图、左视图都是矩形,而俯视图是三角形,因此选项C不符合题意;
正方体的三视图都是形状、大小相同的正方形,因此选项D符合题意;
2.【答案】D
【解析】解:从左边看是一个矩形被分为3部分,上面的分线是实线,下面的分线是虚线.
3.【答案】B
【解析】解:根据主视图和俯视图为长方形可得此几何体为柱体,左视图为圆可得此几何体为圆柱,
4.【答案】D
【解析】解:根据主视图和左视图为矩形判断出是柱体,根据俯视图是圆可判断出这个几何体是圆柱.
5.【答案】D
【解答】
解:根据主视图和左视图为矩形判断出是柱体,根据俯视图是三角形可判断出这个几何体应该是三棱柱.
6.【答案】B
【解析】解:综合主视图和俯视图,底层最少有4个小立方体,第二层最少有2个小立方体,因此搭成这个几何体的小正方体的个数最少是6个.
7.【答案】A
【解析】解:从上面看,可得到左边是一个圆,右边是长方形,一组对边与圆相接;
8.【答案】D
【解析】解:左视图是从左边看到的平面图形,发现从左面看一共有两列,左边一列有2个正方形,右边一列有3个正方形,
9.【答案】B
【解答】解:从正面看去,一共两列,左边有2竖列,右边是1竖列.
故选:B.
10.【答案】C
【解析】解:俯视图是圆形,说明这个几何体的上下有两个面是圆形的,左视图、左视图都是长方形的,于是可以判断这个几何体是圆柱体.
11.【答案】A
【解析】解:易得第一层有2个小正方体,第二层有1个小正方体,一共有3个,
这个几何体的体积为3cm3
12.【答案】B
【解答】
解:由三视图得这个几何体为圆锥,圆锥的母线长为8,底面圆的直径为6,
所以这个几何体的侧面积=12×π×6×8=24π(cm2).
13.【答案】5
【解析】解:根据主视图、左视图可知,其俯视图最多为2×2的正方形,如图所示,
其中数字表示该位置最多能摆放的小立方体的个数,
所以,这个几何体中小正方体的个数最多是5个,
14.【答案】(36+83)
【解析】解:观察三视图知:该几何体为三棱柱,高为3cm,长为4cm,
侧面积为:3×4×3+2×12×4×23=(36+83)cm2.
则这个几何体的侧面积是(36+83)cm2.
15.【答案】19
【解答】
解:由主视图可知,原来的几何体由三层,且有3列,
由左视图可知,搭成的几何体共有3行,
由俯视图易得最底层有5个小立方体,第二层有2个小立方体,第三层有1个小立方体,那么共有5+2+1=8个几何体组成.
若搭成一个大正方体,共需3×3×3=27个小立方体,
所以至少还需27?8=19个小立方体,
故答案为19.
16.【答案】7
【解答】
解:根据题意得:
则搭成该几何体的小正方体最多是1+1+1+2+2=7(个).
故答案为7.
17.【答案】4
【解析】解:设底面半径为r,母线为l,
∵主视图为等腰直角三角形,
∴2r=2l,
∴侧面积S侧=πrl=2πr2=162πcm2,
解得?r=4,l=42,
∴圆锥的高?=4cm,
18.【答案】解:该包装盒的几何形状是直六棱柱,画出的平面展开图如下:
过俯视图的一边AB作正六边形对角线EF的垂线BC、AD,
设CE=x,
因为六边形是正六边形,
所以正六边形的一个内角为120°,
所以∠BEC=60°,故∠EBC=30°,
所以BE=2CE=2x,DF=x,
所以DC=60?2x,
根据正六边形的性质可得AB=BE=2x,由作图步骤可得CD=AB,
所以60?2x=2x,
解得x=15,故2x=30
所以正六边形的边长为30.
所以正六棱柱的侧面为长为40,宽为30的长方形,上下底面是边长为30的正六边形,
将正六边形可以分割为6个边长为30的等边三角形.
∵每个等边三角形的边长为30,
∴每个等边三角形的面积为12×30×30×sin60?=450×32=2253,
∴该包装盒的底面的面积为12×2253=27003.
∵该包装盒的侧面是6个长为40,宽为30的长方形,
∴该包装盒的侧面的面积为6×40×30=7200,
∴该包装盒的表面积为27003+7200.
19.【答案】解:根据题意,这个几何体的主视图和左视图如下图所示:
20.【答案】解:如图所示:
21.【答案】解:由题意可知:该几何体的上面是底面直径为20cm,高为32cm的圆柱,下面是长为30cm,宽为25cm,高为40cm的长方体,
∴表面积为:30×25×2+30×40×2+25×40×2+π×20×32=5900+640π(cm2)
体积为:
30×25×40+π×(20÷2)2×32=30000+3200π(cm3)
答:该几何体的表面积(5900+640π)cm2和体积为(30000+3200π)cm3.
