27.1 图形的相似-2020-2021学年人教版九年级数学下册练习(Word版 含答案)
文档属性
| 名称 | 27.1 图形的相似-2020-2021学年人教版九年级数学下册练习(Word版 含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 103.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-07 12:53:05 | ||
图片预览



文档简介
图形的相似练习
一、选择题
两个相似多边形一组对应边分别为3cm,4.5cm,那么它们的相似比为(????)
A. 23 B. 32 C. 49 D. 94
若a:b=3:4,且a+b=14,则2a?b的值是(????)
A. 4 B. 2 C. 20 D. 14
已知xy=23,则下列式子一定正确的是(????)
A. x=2,y=3 B. 2x=3y C. x?yy=13 D. x+yy=53
如果x:y=1:2,那么下列各式中不成立的是(????)
A. x+yy=32 B. y?xy=12 C. yx=21 D. x+1y+1=23
已知2a?3b=0,则ab的值为(?)
A. 23 B. 2 C. 3 D. 32
将直角三角形的三条边的长度都扩大同样的倍数后得到的三角形(????)
A. 仍是直角三角形 B. 一定是锐角三角形
C. 可能是钝角三角形 D. 一定是钝角三角形
如图,用放大镜将图形放大,这种图形的改变是(????)
A. 相似
B. 平移
C. 轴对称
D. 旋转
若x2=y7=z5,则x+y?z2x+z的值是(????)
A. 67 B. 13 C. 49 D. 4
如图,在矩形、三角形、正五边形、菱形的外边加一个宽度一样的外框,保证外框的边界与原图形对应边平行,则外框与原图不一定相似的是(????)
A. B. C. D.
已知点C是线段AB的黄金分割点,且AC>BC,AB=200,则AC的长度是(????)
A. 200(5?1) B. 100(5?1) C. 100(3?5) D. 50(5?1)
把一个长方形划分成三个全等的长方形,若要使每一个小长方形与原长方形相似,则原长方形的长a与宽b的关系是(????)
A. ab=2 B. ab=3 C. ab=3 D. ab=2
如图,点P(8,6)在△ABC的边AC上,以原点O为位似中心,在第一象限内将△ABC缩小到原来的12,得到△A′B′C′,点P在A′C′上的对应点P′的的坐标为(????)
A. (4,3)
B. (3,4)
C. (5,3)
D. (4,4)
点B是线段AC的黄金分割点,且AB A. 5+12 B. 5?12 C. 5+1 D. 5?1
二、填空题
若2a=3b,则a+bb=______.
如果4是a与8的比例中项,那么a的值为________.
两个相似多边形的面积的比为9?:?16,其中较小的多边形的周长为36?cm,则另一个多边形的周长为________.
已知线段a=2,b=8,则a,b的比例中项是______.
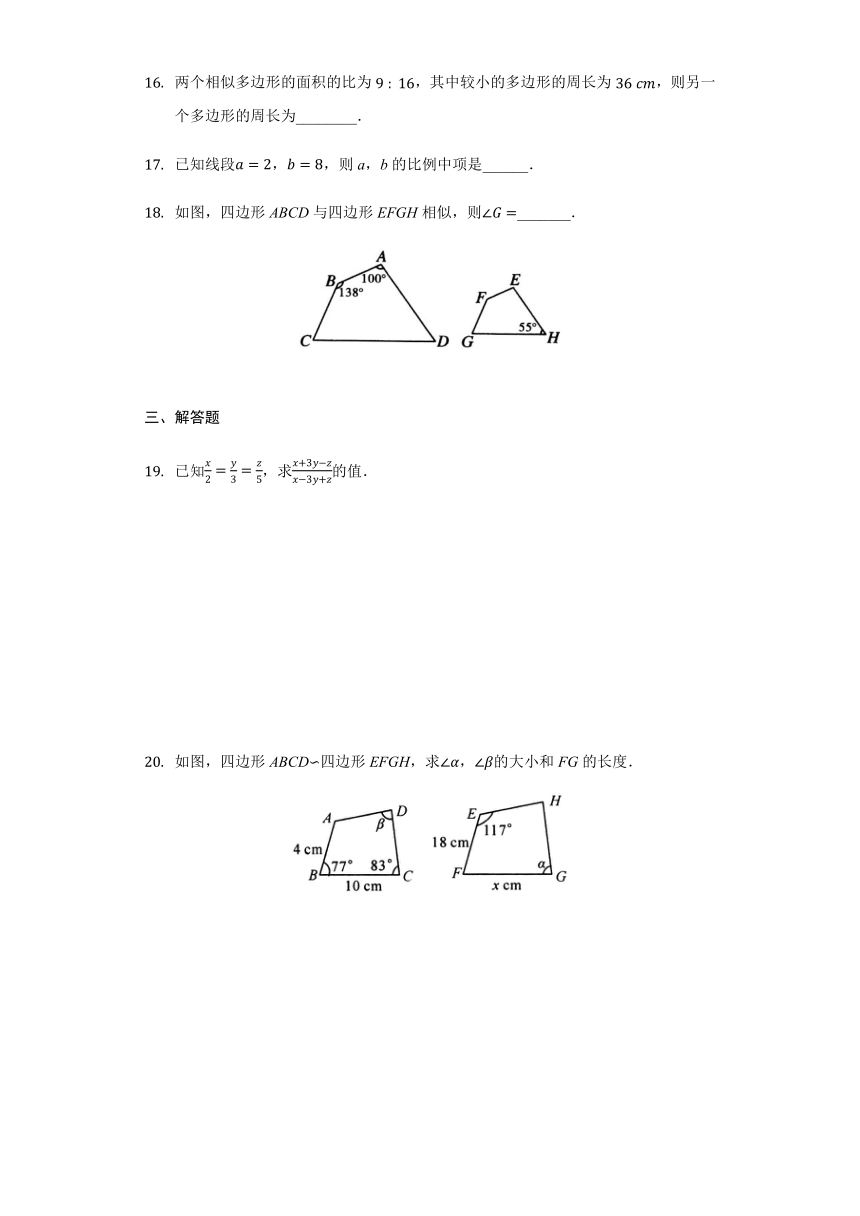
如图,四边形ABCD与四边形EFGH相似,则∠G=_______.
三、解答题
已知x2=y3=z5,求x+3y?zx?3y+z的值.
如图,四边形ABCD∽四边形EFGH,求∠α,∠β的大小和FG的长度.
已知A,B两地的实际距离AB=250?m,而画在一张地图上的距离A′B′=5?cm,求图上距离与实际距离的比.
答案和解析
1.【答案】A
【解析】解:∵两个相似多边形一组对应边分别为3cm,4.5cm,
∴它们的相似比为:34.5=23.
2.【答案】A
【解析】解:由a:b=3:4知3b=4a,
所以b=4a3.
所以由a+b=14得到:a+4a3=14,
解得a=6.
所以b=8.
所以2a?b=2×6?8=4.
3.【答案】D
【解析】解:A.由xy=23,可得3x=2y,故x=2,y=3不一定成立,本选项不合题意;
B.由xy=23,可得3x=2y,故2x=3y不成立,本选项不合题意;
C.由xy=23,可得xy?1=23?1,即x?yy=?13,故x?yy=13不成立,本选项不合题意;
D.由xy=23,可得xy+1=23+1,故x+yy=53,本选项符合题意;
4.【答案】D
【解答】
解:∵x:y=1:2,
∴xy=12,
A.x+yy=xy+yy=12+1=32,故本选项正确;
B,y?xy=1?xy=1?12=12,故本选项正确;
C,yx=1xy=112=21,故本选项正确;
D,x+1y+1不一定等于23,例如,当x=2,y=4时,x+1y+1=2+14+1=35,
故此选项错误,
5.【答案】D
【解答】
解:∵2a?3b=0,
∴2a=3b,
∴ab=32.
6.【答案】A
【解析】解:∵将直角三角形的各边都缩小或扩大同样的倍数后,得到的三角形的三条边与原三角形的三条边对应成比例,
∴两三角形相似.
又∵原来的三角形是直角三角形,而相似三角形的对应角相等,
∴得到的三角形仍是直角三角形.
7.【答案】A
【解析】解:根据相似图形的定义知,用放大镜将图形放大,属于图形的形状相同,大小不相同,所以属于相似变换.
8.【答案】C
【解析】解:设x2=y7=z5=k(K≠0),则x=2k,y=7k,z=5k,
∴x+y?z2x+z=2k+7k?5k4k+5k=49,
9.【答案】A
10.【答案】B
【解析】解:∵点C是线段AB的黄金分割点,且AC>BC,
∴AC=5?12AB,
而AB=200,
∴AC=5?12×200=100(5?1).
11.【答案】B
【解析】解:如图:设AB=b,BE=a3,则BC=a,
∵每一个小长方形与原长方形相似,
∴a3b=ba,
∴3b2=a2,
∴ba=33,
∴ab=333=3,
12.【答案】A
【解答】
解:∵点P(8,6)在△ABC的边AC上,以原点O为位似中心,在第一象限内将△ABC缩小到原来的12,得到△A′B′C′,
∴点P在A′C′上的对应点P′的的坐标为:(4,3).
13.【答案】D
【解答】解:∵点B是线段AC的黄金分割点,且AB∴BC=5?12AC,
∵AC=2,
∴BC=5?1.
14.【答案】52
【解析】解:∵2a=3b,
∴a=32b,
∴a+bb=3b2+bb=52.
15.【答案】2
【解答】
解:∵4是a与8的比例中项,
∴a:4=4:8,
∴8a=16,
解得a=2.
故答案为2.
16.【答案】48cm
【解答】
解:两个相似多边形的面积比是9:16,
面积比是相似比的平方,
则大多边形与小多边形的相似比是4:3.
相似多边形周长的比等于相似比,
因而设大多边形的周长为xcm,
则有x36=43,
解得:x=48.
大多边形的周长为48cm.
故答案为48cm.
17.【答案】4
【解析】解:设线段a,b的比例中项为c,
∵c是长度分别为2、8的两条线段的比例中项,
∴c2=ab=2×8,
即c2=16,
∴c=4(负数舍去).
18.【答案】67°
【解答】
解:∵四边形ABCD与四边形EFGH相似,
∴∠D=∠H=55°,
在四边形ABCD中,∠C=360°?138°?100°?55°=67°,
∴∠G=∠C=67°.
故答案为67°.
19.【答案】解:设x2=y3=z5=k,
则x=2k,y=3k,z=5k,
故原式=2k+9k?5k2k?9k+5k=6k?2k=?3.
20.【答案】解:∵四边形ABCD~四边形EFGH,
∴∠α=∠C=83°,∠A=∠E=117°.
在四边形ABCD中,∠β=360°?77°?83°?117°=83°.
∵四边形ABCD~四边形EFGH,
∴ABEF=BCFG,
即418=10x,
解得x=45.
∴FG=45?cm.
21.【答案】解:取厘米作为共同的长度单位,
AB=250?m=25000?cm,
∴A′B′:AB=5:25000=1:5000.
一、选择题
两个相似多边形一组对应边分别为3cm,4.5cm,那么它们的相似比为(????)
A. 23 B. 32 C. 49 D. 94
若a:b=3:4,且a+b=14,则2a?b的值是(????)
A. 4 B. 2 C. 20 D. 14
已知xy=23,则下列式子一定正确的是(????)
A. x=2,y=3 B. 2x=3y C. x?yy=13 D. x+yy=53
如果x:y=1:2,那么下列各式中不成立的是(????)
A. x+yy=32 B. y?xy=12 C. yx=21 D. x+1y+1=23
已知2a?3b=0,则ab的值为(?)
A. 23 B. 2 C. 3 D. 32
将直角三角形的三条边的长度都扩大同样的倍数后得到的三角形(????)
A. 仍是直角三角形 B. 一定是锐角三角形
C. 可能是钝角三角形 D. 一定是钝角三角形
如图,用放大镜将图形放大,这种图形的改变是(????)
A. 相似
B. 平移
C. 轴对称
D. 旋转
若x2=y7=z5,则x+y?z2x+z的值是(????)
A. 67 B. 13 C. 49 D. 4
如图,在矩形、三角形、正五边形、菱形的外边加一个宽度一样的外框,保证外框的边界与原图形对应边平行,则外框与原图不一定相似的是(????)
A. B. C. D.
已知点C是线段AB的黄金分割点,且AC>BC,AB=200,则AC的长度是(????)
A. 200(5?1) B. 100(5?1) C. 100(3?5) D. 50(5?1)
把一个长方形划分成三个全等的长方形,若要使每一个小长方形与原长方形相似,则原长方形的长a与宽b的关系是(????)
A. ab=2 B. ab=3 C. ab=3 D. ab=2
如图,点P(8,6)在△ABC的边AC上,以原点O为位似中心,在第一象限内将△ABC缩小到原来的12,得到△A′B′C′,点P在A′C′上的对应点P′的的坐标为(????)
A. (4,3)
B. (3,4)
C. (5,3)
D. (4,4)
点B是线段AC的黄金分割点,且AB
二、填空题
若2a=3b,则a+bb=______.
如果4是a与8的比例中项,那么a的值为________.
两个相似多边形的面积的比为9?:?16,其中较小的多边形的周长为36?cm,则另一个多边形的周长为________.
已知线段a=2,b=8,则a,b的比例中项是______.
如图,四边形ABCD与四边形EFGH相似,则∠G=_______.
三、解答题
已知x2=y3=z5,求x+3y?zx?3y+z的值.
如图,四边形ABCD∽四边形EFGH,求∠α,∠β的大小和FG的长度.
已知A,B两地的实际距离AB=250?m,而画在一张地图上的距离A′B′=5?cm,求图上距离与实际距离的比.
答案和解析
1.【答案】A
【解析】解:∵两个相似多边形一组对应边分别为3cm,4.5cm,
∴它们的相似比为:34.5=23.
2.【答案】A
【解析】解:由a:b=3:4知3b=4a,
所以b=4a3.
所以由a+b=14得到:a+4a3=14,
解得a=6.
所以b=8.
所以2a?b=2×6?8=4.
3.【答案】D
【解析】解:A.由xy=23,可得3x=2y,故x=2,y=3不一定成立,本选项不合题意;
B.由xy=23,可得3x=2y,故2x=3y不成立,本选项不合题意;
C.由xy=23,可得xy?1=23?1,即x?yy=?13,故x?yy=13不成立,本选项不合题意;
D.由xy=23,可得xy+1=23+1,故x+yy=53,本选项符合题意;
4.【答案】D
【解答】
解:∵x:y=1:2,
∴xy=12,
A.x+yy=xy+yy=12+1=32,故本选项正确;
B,y?xy=1?xy=1?12=12,故本选项正确;
C,yx=1xy=112=21,故本选项正确;
D,x+1y+1不一定等于23,例如,当x=2,y=4时,x+1y+1=2+14+1=35,
故此选项错误,
5.【答案】D
【解答】
解:∵2a?3b=0,
∴2a=3b,
∴ab=32.
6.【答案】A
【解析】解:∵将直角三角形的各边都缩小或扩大同样的倍数后,得到的三角形的三条边与原三角形的三条边对应成比例,
∴两三角形相似.
又∵原来的三角形是直角三角形,而相似三角形的对应角相等,
∴得到的三角形仍是直角三角形.
7.【答案】A
【解析】解:根据相似图形的定义知,用放大镜将图形放大,属于图形的形状相同,大小不相同,所以属于相似变换.
8.【答案】C
【解析】解:设x2=y7=z5=k(K≠0),则x=2k,y=7k,z=5k,
∴x+y?z2x+z=2k+7k?5k4k+5k=49,
9.【答案】A
10.【答案】B
【解析】解:∵点C是线段AB的黄金分割点,且AC>BC,
∴AC=5?12AB,
而AB=200,
∴AC=5?12×200=100(5?1).
11.【答案】B
【解析】解:如图:设AB=b,BE=a3,则BC=a,
∵每一个小长方形与原长方形相似,
∴a3b=ba,
∴3b2=a2,
∴ba=33,
∴ab=333=3,
12.【答案】A
【解答】
解:∵点P(8,6)在△ABC的边AC上,以原点O为位似中心,在第一象限内将△ABC缩小到原来的12,得到△A′B′C′,
∴点P在A′C′上的对应点P′的的坐标为:(4,3).
13.【答案】D
【解答】解:∵点B是线段AC的黄金分割点,且AB
∵AC=2,
∴BC=5?1.
14.【答案】52
【解析】解:∵2a=3b,
∴a=32b,
∴a+bb=3b2+bb=52.
15.【答案】2
【解答】
解:∵4是a与8的比例中项,
∴a:4=4:8,
∴8a=16,
解得a=2.
故答案为2.
16.【答案】48cm
【解答】
解:两个相似多边形的面积比是9:16,
面积比是相似比的平方,
则大多边形与小多边形的相似比是4:3.
相似多边形周长的比等于相似比,
因而设大多边形的周长为xcm,
则有x36=43,
解得:x=48.
大多边形的周长为48cm.
故答案为48cm.
17.【答案】4
【解析】解:设线段a,b的比例中项为c,
∵c是长度分别为2、8的两条线段的比例中项,
∴c2=ab=2×8,
即c2=16,
∴c=4(负数舍去).
18.【答案】67°
【解答】
解:∵四边形ABCD与四边形EFGH相似,
∴∠D=∠H=55°,
在四边形ABCD中,∠C=360°?138°?100°?55°=67°,
∴∠G=∠C=67°.
故答案为67°.
19.【答案】解:设x2=y3=z5=k,
则x=2k,y=3k,z=5k,
故原式=2k+9k?5k2k?9k+5k=6k?2k=?3.
20.【答案】解:∵四边形ABCD~四边形EFGH,
∴∠α=∠C=83°,∠A=∠E=117°.
在四边形ABCD中,∠β=360°?77°?83°?117°=83°.
∵四边形ABCD~四边形EFGH,
∴ABEF=BCFG,
即418=10x,
解得x=45.
∴FG=45?cm.
21.【答案】解:取厘米作为共同的长度单位,
AB=250?m=25000?cm,
∴A′B′:AB=5:25000=1:5000.
