人教版八年级数学下册同步练习16.1《二次根式》(Word版 含答案)
文档属性
| 名称 | 人教版八年级数学下册同步练习16.1《二次根式》(Word版 含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 32.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-07 12:53:09 | ||
图片预览


文档简介
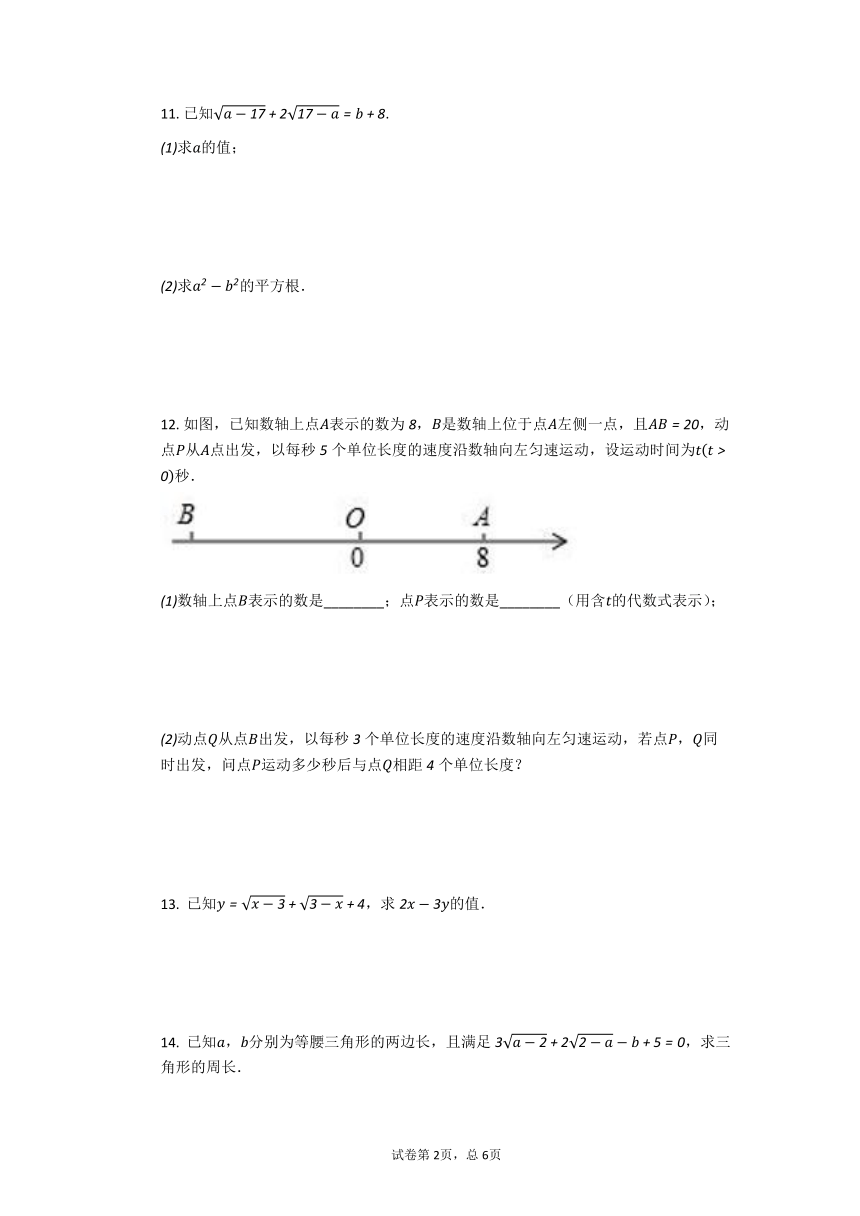
人教版八年级数学下册同步练习16.1《二次根式》
?
1. 下列式子中是二次根式的是(? ? ? ? )
A.a B.x+1 C.x2+2x+1 D.?2?
2. 在式子x2(x>0),2,y+1(y=?2),?2x(x>0),33,x2+1,x+y中,二次根式有(? ? ? ? )
A.2个 B.3个 C.4个 D.5个
3. 要使代数式x+1x?2有意义,则x的取值范围是(? ? ? ? )
A.x≠2 B.x>?1 C.x>?1且x≠2 D.x≥?1且x≠2?
4. 能使x+2有意义的x的取值范围是(? ? ? ? )
A.x≤?2 B.x≥?2 C.x≠?2 D.x>?2
5. 买一个足球需m元,买一个篮球需n元,则买5个足球和4个篮球共需(??)元.
A.9mn B.20mn C.5m+4n D.4m+5n?
6. 若代数式2x2?4x?5的值为7,则x2?2x?2的值为(? ? ? ? )
A.3 B.4 C.5 D.6?
7. 已知2a+2+|b?3|=0,则ab=________. ?
8. 当x=________时,2x?4的值最小.
9. 全国最长、珠海最美的板障山慢行隧道自开通以来迅速成为网红打卡点,隧道全长约为1200米,小海慢跑的速度是a米/秒a>0,小东骑车的速度是小海慢跑速度的3倍,两人匀速通过隧道,那么小海花的时间比小东花的时间多________秒(用含字母a的式子表示). ?
10. 如图是两个边长分别为2a,a的正方形,则△ABC的面积是________.
11. 已知a?17+217?a=b+8.
(1)求a的值;
(2)求a2?b2的平方根.
?
12. 如图,已知数轴上点A表示的数为8,B是数轴上位于点A左侧一点,且AB=20,动点P从A点出发,以每秒5个单位长度的速度沿数轴向左匀速运动,设运动时间为tt>0秒.
(1)数轴上点B表示的数是________;点P表示的数是________(用含t的代数式表示);
(2)动点Q从点B出发,以每秒3个单位长度的速度沿数轴向左匀速运动,若点P,Q同时出发,问点P运动多少秒后与点Q相距4个单位长度?
?
13. 已知y=x?3+3?x+4,求2x?3y的值.
?
14. 已知a,b分别为等腰三角形的两边长,且满足3a?2+22?a?b+5=0,求三角形的周长.
参考答案
人教版八年级数学下册同步练习16.1《二次根式》
一、 选择题
1.
【答案】
C
【解析】
A.a中,当a<0时,不是二次根式,故此选项不合题意;B.x+1中当x2.
【答案】
B
【解析】
根据二次根式的定义对各数分析判断即可得解.
3.
【答案】
D
【解析】
根据被开方数大于等于0,分母不等于0列式计算即可得解.
4.
【答案】
B
【解析】
根据二次根式有意义的条件可得x+2≥0,即可解答本题.
5.
【答案】
C
【解析】
直接利用单价×数量=所需费用进而得出答案.
6.
【答案】
B
【解析】
根据题意得出2x2?4x?5=7,求出x2?2x=6,代入求出即可.
二、 填空题
7.
【答案】
?33
【解析】
根据非负数的性质列方程求出a、b的值,然后代入代数式进行计算即可得解.
8.
【答案】
2
【解析】
根据二次根式的“双重非负性”即“根式内的数或式大于等于零”和“根式的计算结果大于等于零”解答.
9.
【答案】
800a
【解析】
用小海的花的时间-小东花的时间即可求解.即1200a?12003a=24003a=800a米/秒.
10.
【答案】
32a2
【解析】
首先求出BD,BC的长,然后利用三角形的面积公式进行求解即可.
三、 解答题
11.
【答案】
解:(1)a?17+217?a=b+8,
∴ a?17≥0且17?a≥0,
解得:a=17,
代入可得b=?8.
(2)a2?b2的平方根是±172?(?8)2=±15.
【解析】
(1)根据二次根式有意义的条件得出不等式组,求出a即可;
(2)求出a、b的值,再求出平方根即可.
12.
【答案】
?12,8?5t
(2)分两种情况:
①点Q在P的左边时,
5t?3t=20?4,解得t=8;
②点Q在P的右边时,
5t?3t=20+4,解得t=12.
综上所述,点P运动8或12秒后与点Q相距4个单位长度.
【解析】
(1)根据数轴上的点表示的数右边总比左边的数大及数轴上两点间的距离公式即可得点B表示的数及点P表示的数;
(2)分两种情况:①点Q在P的左边时,②点Q在P的右边时,列出方程求解即可.
13.
【答案】
解:根据题意得:x?3≥0,3?x≥0,
所以x=3,y=4,
所以2x?3y=2×3?3×4=?6.
14.
【答案】
解:∵ 3a?2+22?a?b+5=0,
∴ a?2≥0,2?a≥0.
解得:a=2,
∴ b=5,
当2为腰时,三边为2,2,5,由三角形三边关系定理可知,不能构成三角形,
当5为腰时,三边为5,5,2,符合三角形三边关系定理,周长为:5+5+2=12.
【解析】
首先根据3a?2+22?a?b+5=0并利用二次根式有意义的条件求得a、b的值,然后求得等腰三角形的周长即可.
?
1. 下列式子中是二次根式的是(? ? ? ? )
A.a B.x+1 C.x2+2x+1 D.?2?
2. 在式子x2(x>0),2,y+1(y=?2),?2x(x>0),33,x2+1,x+y中,二次根式有(? ? ? ? )
A.2个 B.3个 C.4个 D.5个
3. 要使代数式x+1x?2有意义,则x的取值范围是(? ? ? ? )
A.x≠2 B.x>?1 C.x>?1且x≠2 D.x≥?1且x≠2?
4. 能使x+2有意义的x的取值范围是(? ? ? ? )
A.x≤?2 B.x≥?2 C.x≠?2 D.x>?2
5. 买一个足球需m元,买一个篮球需n元,则买5个足球和4个篮球共需(??)元.
A.9mn B.20mn C.5m+4n D.4m+5n?
6. 若代数式2x2?4x?5的值为7,则x2?2x?2的值为(? ? ? ? )
A.3 B.4 C.5 D.6?
7. 已知2a+2+|b?3|=0,则ab=________. ?
8. 当x=________时,2x?4的值最小.
9. 全国最长、珠海最美的板障山慢行隧道自开通以来迅速成为网红打卡点,隧道全长约为1200米,小海慢跑的速度是a米/秒a>0,小东骑车的速度是小海慢跑速度的3倍,两人匀速通过隧道,那么小海花的时间比小东花的时间多________秒(用含字母a的式子表示). ?
10. 如图是两个边长分别为2a,a的正方形,则△ABC的面积是________.
11. 已知a?17+217?a=b+8.
(1)求a的值;
(2)求a2?b2的平方根.
?
12. 如图,已知数轴上点A表示的数为8,B是数轴上位于点A左侧一点,且AB=20,动点P从A点出发,以每秒5个单位长度的速度沿数轴向左匀速运动,设运动时间为tt>0秒.
(1)数轴上点B表示的数是________;点P表示的数是________(用含t的代数式表示);
(2)动点Q从点B出发,以每秒3个单位长度的速度沿数轴向左匀速运动,若点P,Q同时出发,问点P运动多少秒后与点Q相距4个单位长度?
?
13. 已知y=x?3+3?x+4,求2x?3y的值.
?
14. 已知a,b分别为等腰三角形的两边长,且满足3a?2+22?a?b+5=0,求三角形的周长.
参考答案
人教版八年级数学下册同步练习16.1《二次根式》
一、 选择题
1.
【答案】
C
【解析】
A.a中,当a<0时,不是二次根式,故此选项不合题意;B.x+1中当x2.
【答案】
B
【解析】
根据二次根式的定义对各数分析判断即可得解.
3.
【答案】
D
【解析】
根据被开方数大于等于0,分母不等于0列式计算即可得解.
4.
【答案】
B
【解析】
根据二次根式有意义的条件可得x+2≥0,即可解答本题.
5.
【答案】
C
【解析】
直接利用单价×数量=所需费用进而得出答案.
6.
【答案】
B
【解析】
根据题意得出2x2?4x?5=7,求出x2?2x=6,代入求出即可.
二、 填空题
7.
【答案】
?33
【解析】
根据非负数的性质列方程求出a、b的值,然后代入代数式进行计算即可得解.
8.
【答案】
2
【解析】
根据二次根式的“双重非负性”即“根式内的数或式大于等于零”和“根式的计算结果大于等于零”解答.
9.
【答案】
800a
【解析】
用小海的花的时间-小东花的时间即可求解.即1200a?12003a=24003a=800a米/秒.
10.
【答案】
32a2
【解析】
首先求出BD,BC的长,然后利用三角形的面积公式进行求解即可.
三、 解答题
11.
【答案】
解:(1)a?17+217?a=b+8,
∴ a?17≥0且17?a≥0,
解得:a=17,
代入可得b=?8.
(2)a2?b2的平方根是±172?(?8)2=±15.
【解析】
(1)根据二次根式有意义的条件得出不等式组,求出a即可;
(2)求出a、b的值,再求出平方根即可.
12.
【答案】
?12,8?5t
(2)分两种情况:
①点Q在P的左边时,
5t?3t=20?4,解得t=8;
②点Q在P的右边时,
5t?3t=20+4,解得t=12.
综上所述,点P运动8或12秒后与点Q相距4个单位长度.
【解析】
(1)根据数轴上的点表示的数右边总比左边的数大及数轴上两点间的距离公式即可得点B表示的数及点P表示的数;
(2)分两种情况:①点Q在P的左边时,②点Q在P的右边时,列出方程求解即可.
13.
【答案】
解:根据题意得:x?3≥0,3?x≥0,
所以x=3,y=4,
所以2x?3y=2×3?3×4=?6.
14.
【答案】
解:∵ 3a?2+22?a?b+5=0,
∴ a?2≥0,2?a≥0.
解得:a=2,
∴ b=5,
当2为腰时,三边为2,2,5,由三角形三边关系定理可知,不能构成三角形,
当5为腰时,三边为5,5,2,符合三角形三边关系定理,周长为:5+5+2=12.
【解析】
首先根据3a?2+22?a?b+5=0并利用二次根式有意义的条件求得a、b的值,然后求得等腰三角形的周长即可.
