人教版八年级数学下册19.1《函数》 同步练习(Word版 含答案)
文档属性
| 名称 | 人教版八年级数学下册19.1《函数》 同步练习(Word版 含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 308.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-07 00:00:00 | ||
图片预览


文档简介
人教版八年级数学下册同步练习
19.1《函数》
?
1. 骆驼被称为“沙漠之舟”,它的体温是随时间的变化而变化的,在这一问题中,因变量是(? ? ? ? )
A.沙漠 B.体温 C.时间 D.骆驼
2. 某人要在规定的时间内加工100个零件,则工作效率η与时间t之间的关系中,下列说法正确的是( )
A.数100和η,t都是变量 B.数100和η都是常量
C.η和t是变量 D.数100和t都是常量
3. 半径是R的圆的周长C=2πR,下列说法正确的是( )
A.C,π,R是变量,2是常量
B.C是变量,2,π,R是常量
C.R是变量,2,π,C是常量
D.C,R是变量,2π是常量
4. 在关系式y=2x+5中,当自变量x=6时,因变量y的值为(????????)
A.7 B.14 C.17 D.21?
5. 函数y=?3x?6中,当自变量x增加1时,函数值y就( )
A.增加3 B.增加1 C.减少3 D.减少1?
6. 一根弹簧长8cm,它所挂的质量不超过5kg,并且所挂的物体每增加1kg弹簧就伸长0.5cm,则挂上物体后弹簧的长度ycm与所挂物体的质量x(kg)之间的关系式为(????????)
A.y=0.5x+80≤x≤5 B.y=0.5x?80≤x≤5
C.y=0.5x?80≤x≤5 D.y=0.5x+80≤x≤5
7. 函数y=x?1x?3自变量x的取值范围是( )
A.x≥1且x≠3 B.x≥1 C.x≠3 D.x>1且x≠3?
8. 使函数y=x?2有意义的x的取值范围是( )
A.x<2 B.x>2 C.x≤2 D.x≥2
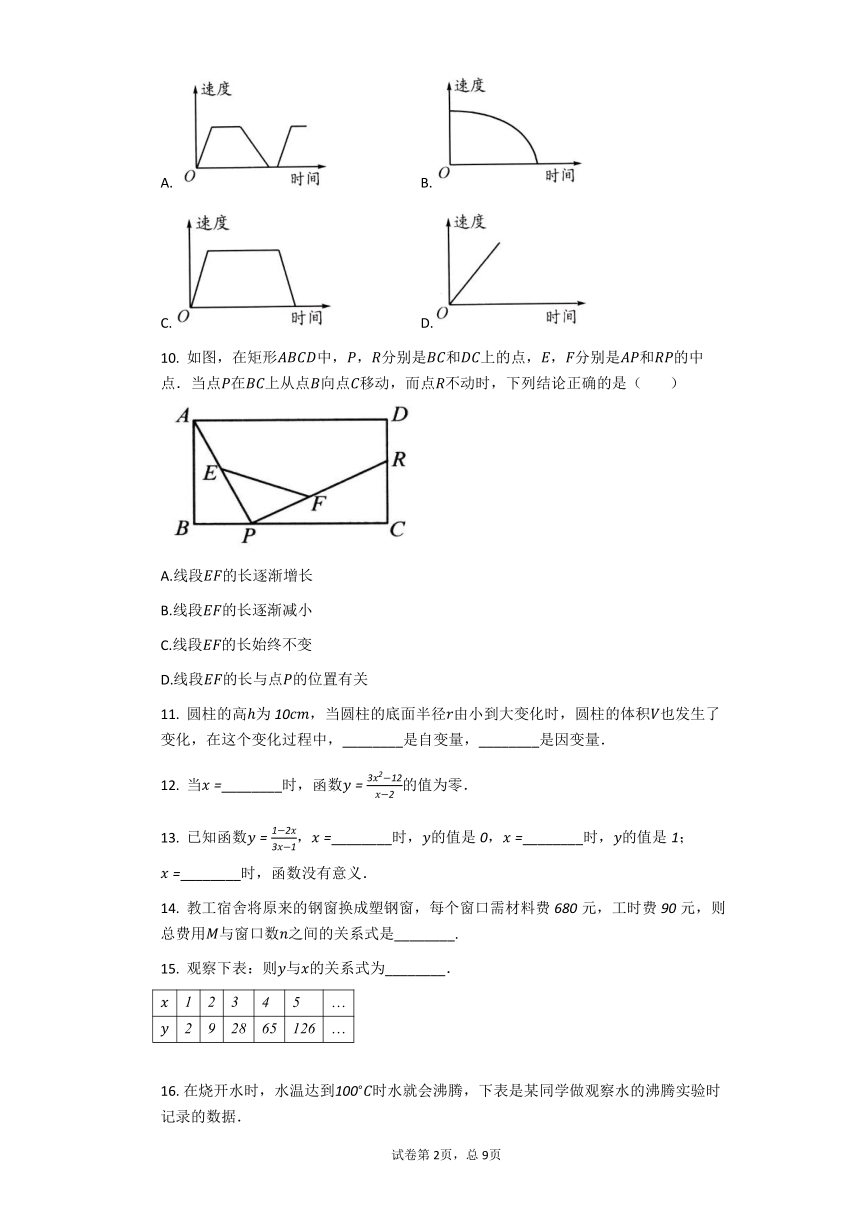
9. 小明一出校门先加速行驶,然后匀速行驶,一段时间后在距家门不远的地方开始减速,而最后停下.下面可以近似地刻画出以上情况的是(? ? ? ? )
A. B.
C. D.
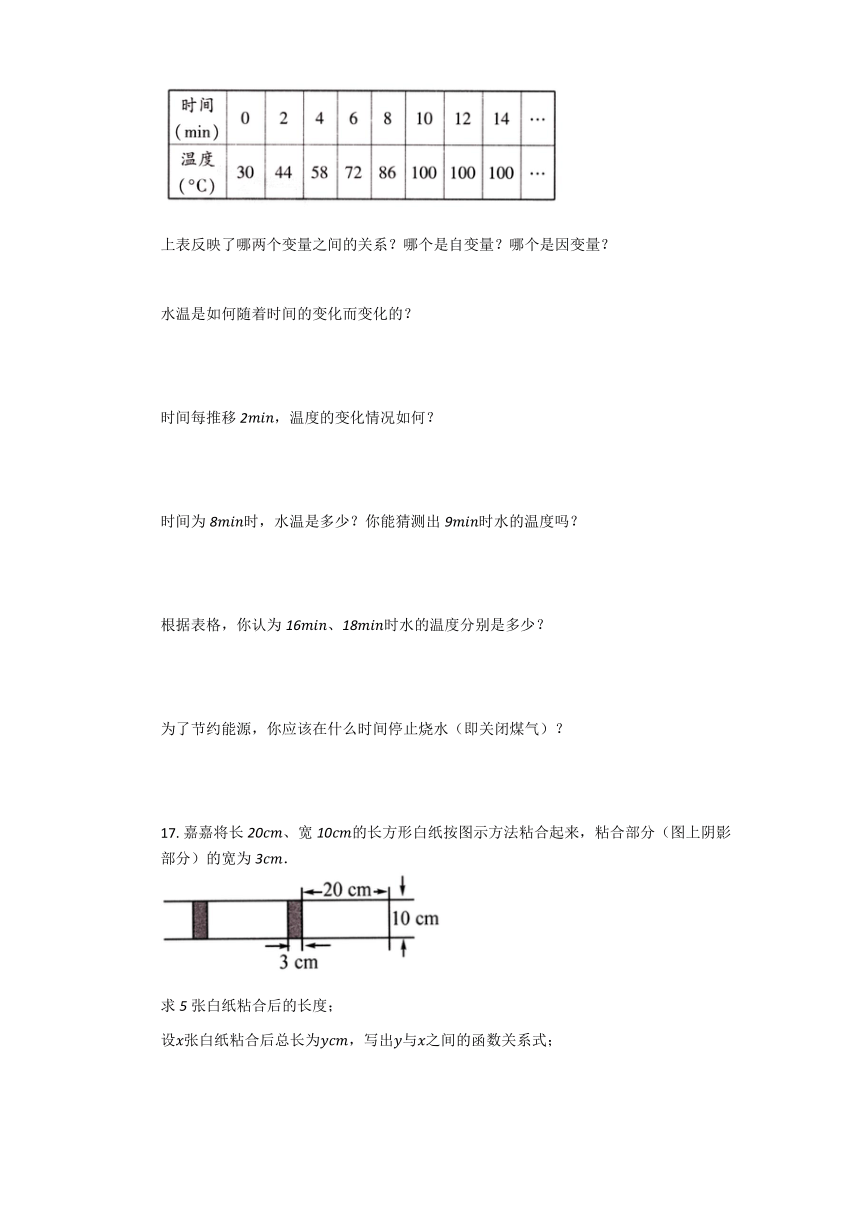
10. 如图,在矩形ABCD中,P,R分别是BC和DC上的点,E,F分别是AP和RP的中点.当点P在BC上从点B向点C移动,而点R不动时,下列结论正确的是(????????)
A.线段EF的长逐渐增长
B.线段EF的长逐渐减小
C.线段EF的长始终不变
D.线段EF的长与点P的位置有关?
11. 圆柱的高?为10cm,当圆柱的底面半径r由小到大变化时,圆柱的体积V也发生了变化,在这个变化过程中,________是自变量,________是因变量.
12. 当x=________时,函数y=3x2?12x?2的值为零. ?
13. 已知函数y=1?2x3x?1,x=________时,y的值是0,x=________时,y的值是1;x=________时,函数没有意义. ?
14. 教工宿舍将原来的钢窗换成塑钢窗,每个窗口需材料费680元,工时费90元,则总费用M与窗口数n之间的关系式是________. ?
15. 观察下表:则y与x的关系式为________.
x
1
2
3
4
5
…
y
2
9
28
65
126
…
?
16. 在烧开水时,水温达到100?C时水就会沸腾,下表是某同学做观察水的沸腾实验时记录的数据.
上表反映了哪两个变量之间的关系?哪个是自变量?哪个是因变量?
水温是如何随着时间的变化而变化的?
时间每推移2min,温度的变化情况如何?
时间为8min时,水温是多少?你能猜测出9min时水的温度吗?
根据表格,你认为16min、18min时水的温度分别是多少?
为了节约能源,你应该在什么时间停止烧水(即关闭煤气)?
?
17. 嘉嘉将长20cm、宽10cm的长方形白纸按图示方法粘合起来,粘合部分(图上阴影部分)的宽为3cm.
求5张白纸粘合后的长度;
设x张白纸粘合后总长为ycm,写出y与x之间的函数关系式;
求当x=20时的y值,并说明它在题目中的实际意义.
?
18. 某市电力公司采用分段计费的方法计算电费.每月用电不超过100度时,按每度0.57元计算费用,每月用电超过100度时,超过部分按每度0.60元计算.
设每月用电x度时,应交电费y元,写出y与x之间的关系式,并写出自变量的取值范围;
小王家1月份用了125度电,应交电费多少元?
小王家3月份交电费45.6元,则小王家3月份用了多少度电?
?
19. 已知三角形的三边长分别为10cm,7cm,xcm,它的周长为ycm.
(1)求y关于x的函数解析式和自变量x的取值范围;
(2)当x=6cm时,求三角形的周长;
(3)当x=18cm时,能求出三角形的周长吗?为什么?
参考答案
人教版八年级数学下册同步练习 18.2《特殊的平行四边形》
一、 选择题 (本题共计 10 小题 ,每题 3 分 ,共计30分 )
1.
【答案】
B
2.
【答案】
C
【解答】
解:某人要在规定的时间内加工100个零件,则工作效率η与时间t之间的关系中:η和t是变量,零件的个数100是常量.
故选:C.
3.
【答案】
D
【解答】
解:由C=2πR,得
C、R是变量,2π是常量,故D正确;
故选:D.
4.
【答案】
C
5.
【答案】
C
【解答】
解:将x+1代入原函数得:y=?3(x+1)?6=?3x?9;
所以,函数值减小了3;
故本题选C.
6.
【答案】
D
7.
【答案】
A
【解答】
解:根据题意得,x?1≥0且x?3≠0,
解得x≥1且x≠3.
故选A.
8.
【答案】
D
【解答】
解:由题意得,x?2≥0,
解得x≥2,
故选D.
9.
【答案】
C
10.
【答案】
C
【解答】
解:连接AR,
∵ 矩形ABCD固定不变,R在CD的位置不变,
∴ AD和DR不变,
∵ 由勾股定理得:?AB=AD2+DR2,
∴ AR的长不变,
∵ E、F分别为AP、RP的中点,
∴ EF=12AB,
即线段EF的长始终不变,
故选C.
二、 填空题 (本题共计 5 小题 ,每题 3 分 ,共计15分 )
11.
【答案】
r,V
【解答】
解:因为圆柱体积V=π???r2,
由上式可知,V随着r的变化而变化,
所以r是自变量,V是因变量.
故答案为:r;V.
12.
【答案】
?2
【解答】
解:令3x2?12x?2=0,
去分母得,3x2?12=0,
移项系数化为1得,x2=4,
x=2或x=?2.
检验:当x=2时,x?2=0,故x=2不是原方程的解;
当x=?2时,x?2≠0,故x=?2是原方程的解.
故答案为?2.
13.
【答案】
12,25,13
【解答】
解:令y=0,则1?2x3x?1=0,解之得:x=12;
令y=1,则1?2x3x?1=1,解之得:x=25;
当3x?1=0即x=13时,函数没有意义.
14.
【答案】
M=770n
15.
【答案】
y=x3+1
【解答】
解:当x=1时,y=13+1=2;
当x=2时,y=22+1=9;
当x=3时,y=33+1=28;
…
由此可得出y=x3+1.
三、 解答题 (本题共计 4 小题 ,每题 10 分 ,共计40分 )
16.
【答案】
答:时间与温度;时间是自变量;温度是因变量
答:0?10分钟,水温随时间每增加1分钟而升高7?C,10分钟之后,水湿不随时间变化始终为100?C
答:升高14?C
答:86?C? ??93?C
答:100?C
答:10分钟时刻
17.
【答案】
88cm
y=17x+3
当x=20时,y=17×20+3=343,∴ 实际意义是20张白纸粘合后的长度是343cm.
【解答】
解:由题意,得20×5?3×5?1=88cm,∴ 5张白纸粘合后的长度是88cm.
y=20x?3x?1,即y=17x+3.
18.
【答案】
y=0.57x0≤x≤1000.6x?3x>100
72元
80度
【解答】
解:由题意得:当0≤x≤100时,y=0.57x,
当x>100时,y=100×0.57+x?100×0.6=0.6x?3.
则y关于x的关系式y=0.57x0≤x≤1000.6x?3x>100
把x=125代入y=0.6x?3,得y=72元.
设小王家三月份用电x度,据题意得.
0.57x=45.6,解得x=80(度)
19.
【答案】
解:(1)由题意可得出:y=10+7+x=17+x.
∵ 10?7∴ 3(2)当x=6时,y=17+6=23cm.
(3)∵ x=18不在范围3∴ 不能求三角形的周长.
【解答】
解:(1)由题意可得出:y=10+7+x=17+x.
∵ 10?7∴ 3(2)当x=6时,y=17+6=23cm.
(3)∵ x=18不在范围3∴ 不能求三角形的周长.
19.1《函数》
?
1. 骆驼被称为“沙漠之舟”,它的体温是随时间的变化而变化的,在这一问题中,因变量是(? ? ? ? )
A.沙漠 B.体温 C.时间 D.骆驼
2. 某人要在规定的时间内加工100个零件,则工作效率η与时间t之间的关系中,下列说法正确的是( )
A.数100和η,t都是变量 B.数100和η都是常量
C.η和t是变量 D.数100和t都是常量
3. 半径是R的圆的周长C=2πR,下列说法正确的是( )
A.C,π,R是变量,2是常量
B.C是变量,2,π,R是常量
C.R是变量,2,π,C是常量
D.C,R是变量,2π是常量
4. 在关系式y=2x+5中,当自变量x=6时,因变量y的值为(????????)
A.7 B.14 C.17 D.21?
5. 函数y=?3x?6中,当自变量x增加1时,函数值y就( )
A.增加3 B.增加1 C.减少3 D.减少1?
6. 一根弹簧长8cm,它所挂的质量不超过5kg,并且所挂的物体每增加1kg弹簧就伸长0.5cm,则挂上物体后弹簧的长度ycm与所挂物体的质量x(kg)之间的关系式为(????????)
A.y=0.5x+80≤x≤5 B.y=0.5x?80≤x≤5
C.y=0.5x?80≤x≤5 D.y=0.5x+80≤x≤5
7. 函数y=x?1x?3自变量x的取值范围是( )
A.x≥1且x≠3 B.x≥1 C.x≠3 D.x>1且x≠3?
8. 使函数y=x?2有意义的x的取值范围是( )
A.x<2 B.x>2 C.x≤2 D.x≥2
9. 小明一出校门先加速行驶,然后匀速行驶,一段时间后在距家门不远的地方开始减速,而最后停下.下面可以近似地刻画出以上情况的是(? ? ? ? )
A. B.
C. D.
10. 如图,在矩形ABCD中,P,R分别是BC和DC上的点,E,F分别是AP和RP的中点.当点P在BC上从点B向点C移动,而点R不动时,下列结论正确的是(????????)
A.线段EF的长逐渐增长
B.线段EF的长逐渐减小
C.线段EF的长始终不变
D.线段EF的长与点P的位置有关?
11. 圆柱的高?为10cm,当圆柱的底面半径r由小到大变化时,圆柱的体积V也发生了变化,在这个变化过程中,________是自变量,________是因变量.
12. 当x=________时,函数y=3x2?12x?2的值为零. ?
13. 已知函数y=1?2x3x?1,x=________时,y的值是0,x=________时,y的值是1;x=________时,函数没有意义. ?
14. 教工宿舍将原来的钢窗换成塑钢窗,每个窗口需材料费680元,工时费90元,则总费用M与窗口数n之间的关系式是________. ?
15. 观察下表:则y与x的关系式为________.
x
1
2
3
4
5
…
y
2
9
28
65
126
…
?
16. 在烧开水时,水温达到100?C时水就会沸腾,下表是某同学做观察水的沸腾实验时记录的数据.
上表反映了哪两个变量之间的关系?哪个是自变量?哪个是因变量?
水温是如何随着时间的变化而变化的?
时间每推移2min,温度的变化情况如何?
时间为8min时,水温是多少?你能猜测出9min时水的温度吗?
根据表格,你认为16min、18min时水的温度分别是多少?
为了节约能源,你应该在什么时间停止烧水(即关闭煤气)?
?
17. 嘉嘉将长20cm、宽10cm的长方形白纸按图示方法粘合起来,粘合部分(图上阴影部分)的宽为3cm.
求5张白纸粘合后的长度;
设x张白纸粘合后总长为ycm,写出y与x之间的函数关系式;
求当x=20时的y值,并说明它在题目中的实际意义.
?
18. 某市电力公司采用分段计费的方法计算电费.每月用电不超过100度时,按每度0.57元计算费用,每月用电超过100度时,超过部分按每度0.60元计算.
设每月用电x度时,应交电费y元,写出y与x之间的关系式,并写出自变量的取值范围;
小王家1月份用了125度电,应交电费多少元?
小王家3月份交电费45.6元,则小王家3月份用了多少度电?
?
19. 已知三角形的三边长分别为10cm,7cm,xcm,它的周长为ycm.
(1)求y关于x的函数解析式和自变量x的取值范围;
(2)当x=6cm时,求三角形的周长;
(3)当x=18cm时,能求出三角形的周长吗?为什么?
参考答案
人教版八年级数学下册同步练习 18.2《特殊的平行四边形》
一、 选择题 (本题共计 10 小题 ,每题 3 分 ,共计30分 )
1.
【答案】
B
2.
【答案】
C
【解答】
解:某人要在规定的时间内加工100个零件,则工作效率η与时间t之间的关系中:η和t是变量,零件的个数100是常量.
故选:C.
3.
【答案】
D
【解答】
解:由C=2πR,得
C、R是变量,2π是常量,故D正确;
故选:D.
4.
【答案】
C
5.
【答案】
C
【解答】
解:将x+1代入原函数得:y=?3(x+1)?6=?3x?9;
所以,函数值减小了3;
故本题选C.
6.
【答案】
D
7.
【答案】
A
【解答】
解:根据题意得,x?1≥0且x?3≠0,
解得x≥1且x≠3.
故选A.
8.
【答案】
D
【解答】
解:由题意得,x?2≥0,
解得x≥2,
故选D.
9.
【答案】
C
10.
【答案】
C
【解答】
解:连接AR,
∵ 矩形ABCD固定不变,R在CD的位置不变,
∴ AD和DR不变,
∵ 由勾股定理得:?AB=AD2+DR2,
∴ AR的长不变,
∵ E、F分别为AP、RP的中点,
∴ EF=12AB,
即线段EF的长始终不变,
故选C.
二、 填空题 (本题共计 5 小题 ,每题 3 分 ,共计15分 )
11.
【答案】
r,V
【解答】
解:因为圆柱体积V=π???r2,
由上式可知,V随着r的变化而变化,
所以r是自变量,V是因变量.
故答案为:r;V.
12.
【答案】
?2
【解答】
解:令3x2?12x?2=0,
去分母得,3x2?12=0,
移项系数化为1得,x2=4,
x=2或x=?2.
检验:当x=2时,x?2=0,故x=2不是原方程的解;
当x=?2时,x?2≠0,故x=?2是原方程的解.
故答案为?2.
13.
【答案】
12,25,13
【解答】
解:令y=0,则1?2x3x?1=0,解之得:x=12;
令y=1,则1?2x3x?1=1,解之得:x=25;
当3x?1=0即x=13时,函数没有意义.
14.
【答案】
M=770n
15.
【答案】
y=x3+1
【解答】
解:当x=1时,y=13+1=2;
当x=2时,y=22+1=9;
当x=3时,y=33+1=28;
…
由此可得出y=x3+1.
三、 解答题 (本题共计 4 小题 ,每题 10 分 ,共计40分 )
16.
【答案】
答:时间与温度;时间是自变量;温度是因变量
答:0?10分钟,水温随时间每增加1分钟而升高7?C,10分钟之后,水湿不随时间变化始终为100?C
答:升高14?C
答:86?C? ??93?C
答:100?C
答:10分钟时刻
17.
【答案】
88cm
y=17x+3
当x=20时,y=17×20+3=343,∴ 实际意义是20张白纸粘合后的长度是343cm.
【解答】
解:由题意,得20×5?3×5?1=88cm,∴ 5张白纸粘合后的长度是88cm.
y=20x?3x?1,即y=17x+3.
18.
【答案】
y=0.57x0≤x≤1000.6x?3x>100
72元
80度
【解答】
解:由题意得:当0≤x≤100时,y=0.57x,
当x>100时,y=100×0.57+x?100×0.6=0.6x?3.
则y关于x的关系式y=0.57x0≤x≤1000.6x?3x>100
把x=125代入y=0.6x?3,得y=72元.
设小王家三月份用电x度,据题意得.
0.57x=45.6,解得x=80(度)
19.
【答案】
解:(1)由题意可得出:y=10+7+x=17+x.
∵ 10?7
(3)∵ x=18不在范围3
【解答】
解:(1)由题意可得出:y=10+7+x=17+x.
∵ 10?7
(3)∵ x=18不在范围3
