人教版八年级数学下册同步练习 18.1《平行四边形》(Word版 含答案)
文档属性
| 名称 | 人教版八年级数学下册同步练习 18.1《平行四边形》(Word版 含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 702.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-07 12:57:41 | ||
图片预览


文档简介
人教版八年级数学下册同步练习
18.1《平行四边形》
?
1. 能判定四边形ABCD为平行四边形的条件是(? ? ? ? )
A.AB?//?CD,AD=BC B.∠A=∠B,∠C=∠D
C.AB=CD,AD=BC D.AB=AD,CB=CD
2. 如图,?ABCD中,过对角线BD上一点P作EF//BC,GH//AB,图中面积相等的平行四边形有(? ? ? ? )
A.2对 B.3对 C.4对 D.5对?
3. 如图,点A是直线l外一点,在l上取两点B,C,分别以A,C为圆心,BC,AB的长为半径作弧,两弧交于点D,分别连接AB,AD,CD.若∠ABC+∠ADC=120?,则∠A的度数是(? ? ? ? )
A.100? B.110? C.120? D.125??
4. 如图,在四边形ABCD中,对角线AC,BD相交于点E,∠CBD=90?,BC=4,BE=ED=3,AC=10,则四边形ABCD的面积为(? ? ? ? )
A.6 B.12 C.20 D.24
5. 如图,在?ABCD中,E,F分别在BC,AD上,若想要使四边形AFCE为平行四边形,需添加一个条件,这个条件不可以是(? ? ? ? )
A.AF=CE B.AE=CF C.∠BAE=∠FCD D.∠BEA=∠FCE?
6. 如果一个四边形的三个内角度数依次如下,那么其中是平行四边形的是(? ? ? ? )
A.88?,108?,88? B.88?,104?,88?
C.88?,92?,92? D.88?,92?,88??
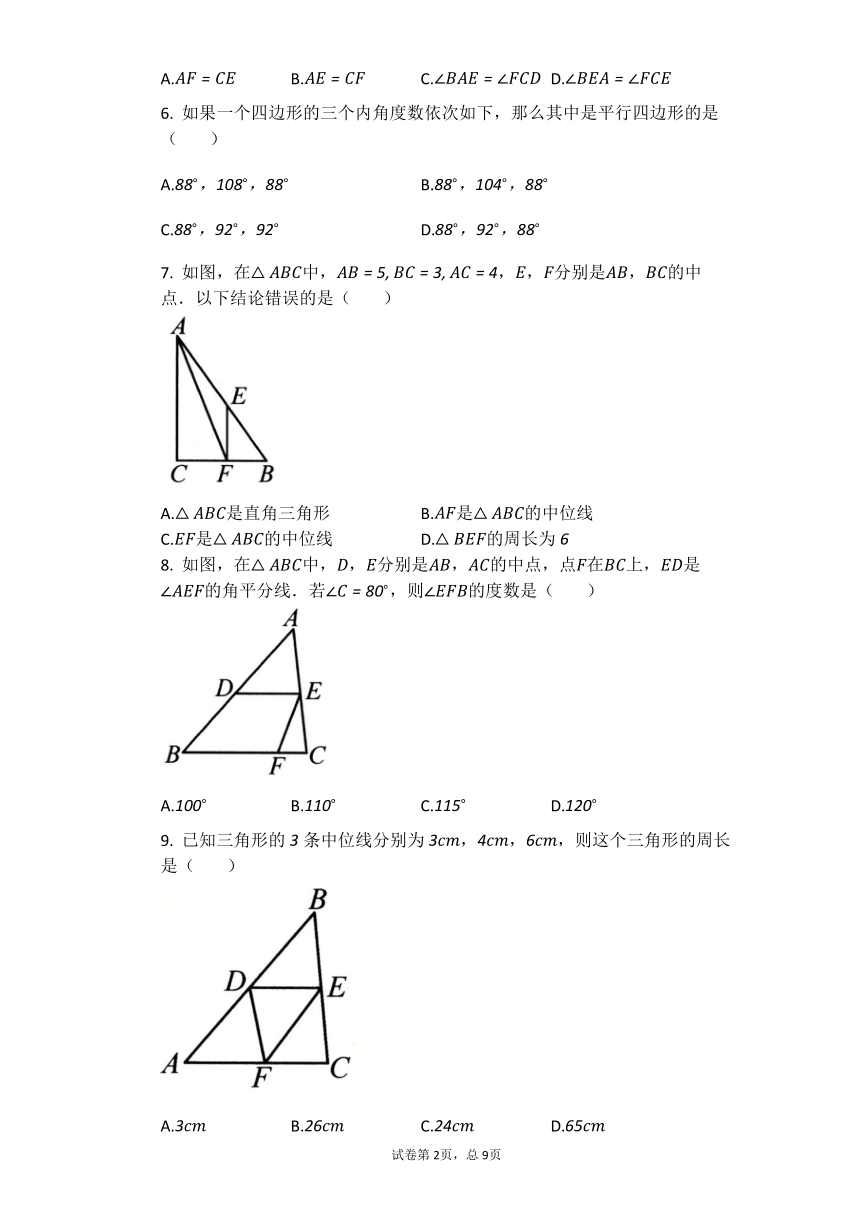
7. 如图,在△ABC中,AB=5,BC=3,AC=4,E,F分别是AB,BC的中点.以下结论错误的是(? ? ? ? )
A.△ABC是直角三角形 B.AF是△ABC的中位线
C.EF是△ABC的中位线 D.△BEF的周长为6
8. 如图,在△ABC中,D,E分别是AB,AC的中点,点F在BC上,ED是∠AEF的角平分线.若∠C=80?,则∠EFB的度数是(? ? ? ? )
A.100? B.110? C.115? D.120??
9. 已知三角形的3条中位线分别为3cm,4cm,6cm,则这个三角形的周长是(? ? ? ? )
A.3cm B.26cm C.24cm D.65cm
10. 下列叙述不正确的是( )
A.一个三角形必有三条中位线
B.一个三角形必有三条中线
C.三角形的一条中线分成的两个三角形的面积相等
D.三角形的一条中位线分成的两部分面积相等?
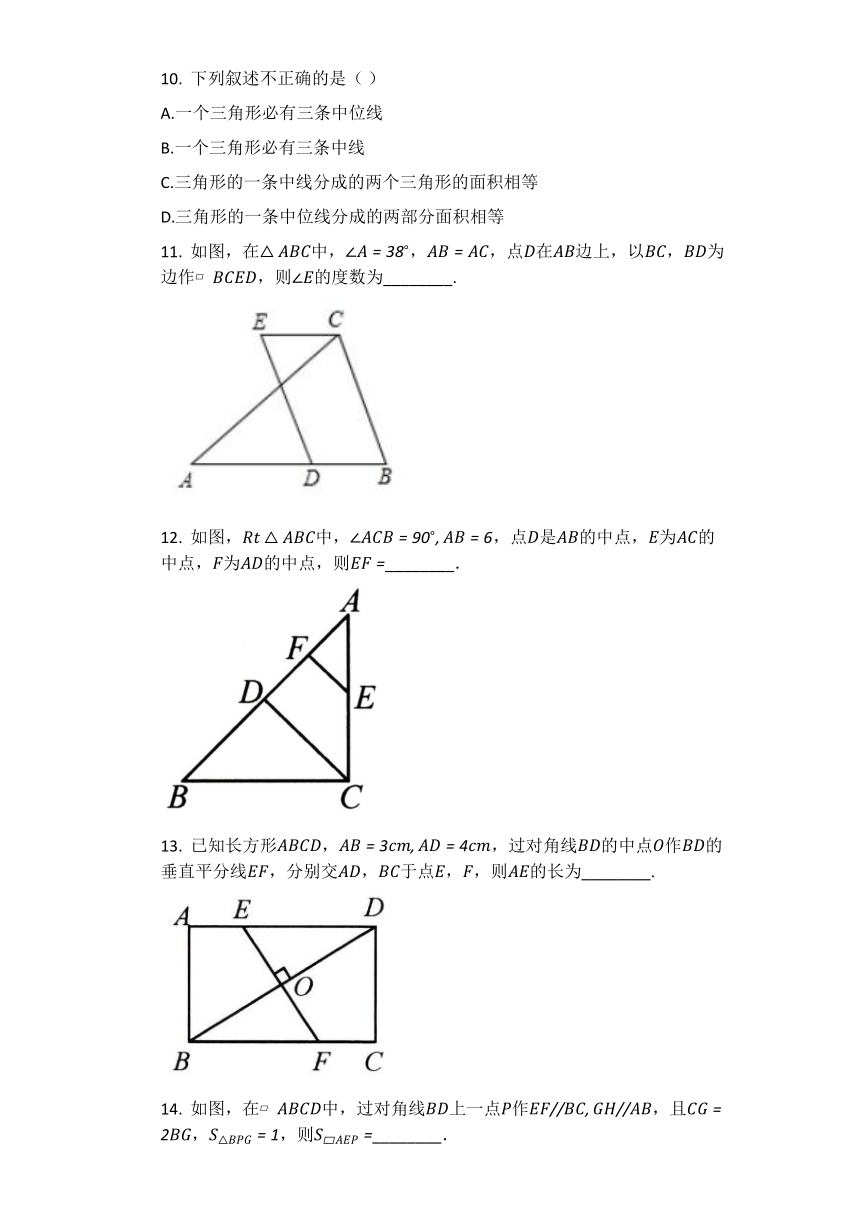
11. 如图,在△ABC中,∠A=38?,AB=AC,点D在AB边上,以BC,BD为边作?BCED,则∠E的度数为________.
12. 如图,Rt△ABC中,∠ACB=90?,AB=6,点D是AB的中点,E为AC的中点,F为AD的中点,则EF=________.
13. 已知长方形ABCD,AB=3cm,AD=4cm,过对角线BD的中点O作BD的垂直平分线EF,分别交AD,BC于点E,F,则AE的长为________.
?
14. 如图,在?ABCD中,过对角线BD上一点P作EF//BC,GH//AB,且CG=2BG,S△BPG=1,则S?AEP=________.
?
15. 如图,在?ABCD中,O是对角线AC的中点,过点O的直线交AD的延长线于点E,交CB的延长线于点F,求证:BF=DE.
?
16. 如图,在△ABC中,D,E,F分别是边AB,BC,AC的中点,以这些点为顶点,在图中,你能画出多少个平行四边形?为什么?
?
17. 如图,已知△ABF,△ACD,△BCE都是等边三角形,求证:四边形ADEF是平行四边形.
?
18. 如图,在四边形ABCD中,AB=CD,M,N分别为AD,BC的中点,BA,CD的延长线分别交MN的延长线于点P,Q.求证:∠APM=∠DQM.
参考答案
人教版八年级数学下册同步练习 18.1《平行四边形》
一、 选择题 (本题共计 10 小题 ,每题 3 分 ,共计30分 )
1.
【答案】
C
2.
【答案】
B
3.
【答案】
C
4.
【答案】
D
5.
【答案】
B
6.
【答案】
D
7.
【答案】
B
8.
【答案】
A
9.
【答案】
B
10.
【答案】
D
二、 填空题 (本题共计 4 小题 ,每题 3 分 ,共计12分 )
11.
【答案】
71?
12.
【答案】
1.5
13.
【答案】
78
14.
【答案】
4
三、 解答题 (本题共计 4 小题 ,每题 10 分 ,共计40分 )
15.
【答案】
证明:∵四边形ABCD为平行四边形,
∴AE//CF且AD=BC,
∴∠E=∠F.
又∵O为对角线AC的中点,
∴AO=CO,
在△AEO与△CFO中,
∠E=∠F,∠AOE=∠COF,AO=CO,
∴△AEO?△CFO,
∴AE=CF.
又∵AD=BC,
∴AE?AD=CF?BC,
∴DE=BF.
16.
【答案】
解:画出3个平行四边形,有平行四边形ADEF,平行四边形CFDE,平行四边形BEFD.
理由如下:
∵ D,E,F分别是△ABC的边AB,BC,AC的中点,
∴ EF//AB,DF//BC,
∴ 四边形BEFD是平行四边形,
同理四边形ADEF是平行四边形,四边形CFDE是平行四边形;
综上所述,能画出3个平行四边形.
17.
【答案】
证明:∵ △ABF,△BCE都是等边△
∴ ∠FBA=∠EBC=60?,AB=BF=AF,BC=BE=EC
∴ ∠FBA?∠EBA=∠EBC?∠EBA
即∠FBE=∠CBA
又∵AB=BF,BC=BE
∴ △FBE?△ABC(SAS)
∴ AC=EF.
∵ △ACD得等边△
∴ AC=AD
∴ EF=AD
同理:AF=DE
∴ 四边形ADEF是平行四边形.
18.
【答案】
证明:连结AC,取AC的中点H,
连结NH,MH.
∵ N,H分别为BC,AC的中点,
∴ NH=//12AB?,
∴ ∠APM=∠HNM,
同理:MH=//12CD,
∴ ∠DQM=∠HMN.
∵ AB=CD,
∴ MH=NH,
∴ ∠HMN=∠HNM,
∴ ∠APM=∠DQM.
18.1《平行四边形》
?
1. 能判定四边形ABCD为平行四边形的条件是(? ? ? ? )
A.AB?//?CD,AD=BC B.∠A=∠B,∠C=∠D
C.AB=CD,AD=BC D.AB=AD,CB=CD
2. 如图,?ABCD中,过对角线BD上一点P作EF//BC,GH//AB,图中面积相等的平行四边形有(? ? ? ? )
A.2对 B.3对 C.4对 D.5对?
3. 如图,点A是直线l外一点,在l上取两点B,C,分别以A,C为圆心,BC,AB的长为半径作弧,两弧交于点D,分别连接AB,AD,CD.若∠ABC+∠ADC=120?,则∠A的度数是(? ? ? ? )
A.100? B.110? C.120? D.125??
4. 如图,在四边形ABCD中,对角线AC,BD相交于点E,∠CBD=90?,BC=4,BE=ED=3,AC=10,则四边形ABCD的面积为(? ? ? ? )
A.6 B.12 C.20 D.24
5. 如图,在?ABCD中,E,F分别在BC,AD上,若想要使四边形AFCE为平行四边形,需添加一个条件,这个条件不可以是(? ? ? ? )
A.AF=CE B.AE=CF C.∠BAE=∠FCD D.∠BEA=∠FCE?
6. 如果一个四边形的三个内角度数依次如下,那么其中是平行四边形的是(? ? ? ? )
A.88?,108?,88? B.88?,104?,88?
C.88?,92?,92? D.88?,92?,88??
7. 如图,在△ABC中,AB=5,BC=3,AC=4,E,F分别是AB,BC的中点.以下结论错误的是(? ? ? ? )
A.△ABC是直角三角形 B.AF是△ABC的中位线
C.EF是△ABC的中位线 D.△BEF的周长为6
8. 如图,在△ABC中,D,E分别是AB,AC的中点,点F在BC上,ED是∠AEF的角平分线.若∠C=80?,则∠EFB的度数是(? ? ? ? )
A.100? B.110? C.115? D.120??
9. 已知三角形的3条中位线分别为3cm,4cm,6cm,则这个三角形的周长是(? ? ? ? )
A.3cm B.26cm C.24cm D.65cm
10. 下列叙述不正确的是( )
A.一个三角形必有三条中位线
B.一个三角形必有三条中线
C.三角形的一条中线分成的两个三角形的面积相等
D.三角形的一条中位线分成的两部分面积相等?
11. 如图,在△ABC中,∠A=38?,AB=AC,点D在AB边上,以BC,BD为边作?BCED,则∠E的度数为________.
12. 如图,Rt△ABC中,∠ACB=90?,AB=6,点D是AB的中点,E为AC的中点,F为AD的中点,则EF=________.
13. 已知长方形ABCD,AB=3cm,AD=4cm,过对角线BD的中点O作BD的垂直平分线EF,分别交AD,BC于点E,F,则AE的长为________.
?
14. 如图,在?ABCD中,过对角线BD上一点P作EF//BC,GH//AB,且CG=2BG,S△BPG=1,则S?AEP=________.
?
15. 如图,在?ABCD中,O是对角线AC的中点,过点O的直线交AD的延长线于点E,交CB的延长线于点F,求证:BF=DE.
?
16. 如图,在△ABC中,D,E,F分别是边AB,BC,AC的中点,以这些点为顶点,在图中,你能画出多少个平行四边形?为什么?
?
17. 如图,已知△ABF,△ACD,△BCE都是等边三角形,求证:四边形ADEF是平行四边形.
?
18. 如图,在四边形ABCD中,AB=CD,M,N分别为AD,BC的中点,BA,CD的延长线分别交MN的延长线于点P,Q.求证:∠APM=∠DQM.
参考答案
人教版八年级数学下册同步练习 18.1《平行四边形》
一、 选择题 (本题共计 10 小题 ,每题 3 分 ,共计30分 )
1.
【答案】
C
2.
【答案】
B
3.
【答案】
C
4.
【答案】
D
5.
【答案】
B
6.
【答案】
D
7.
【答案】
B
8.
【答案】
A
9.
【答案】
B
10.
【答案】
D
二、 填空题 (本题共计 4 小题 ,每题 3 分 ,共计12分 )
11.
【答案】
71?
12.
【答案】
1.5
13.
【答案】
78
14.
【答案】
4
三、 解答题 (本题共计 4 小题 ,每题 10 分 ,共计40分 )
15.
【答案】
证明:∵四边形ABCD为平行四边形,
∴AE//CF且AD=BC,
∴∠E=∠F.
又∵O为对角线AC的中点,
∴AO=CO,
在△AEO与△CFO中,
∠E=∠F,∠AOE=∠COF,AO=CO,
∴△AEO?△CFO,
∴AE=CF.
又∵AD=BC,
∴AE?AD=CF?BC,
∴DE=BF.
16.
【答案】
解:画出3个平行四边形,有平行四边形ADEF,平行四边形CFDE,平行四边形BEFD.
理由如下:
∵ D,E,F分别是△ABC的边AB,BC,AC的中点,
∴ EF//AB,DF//BC,
∴ 四边形BEFD是平行四边形,
同理四边形ADEF是平行四边形,四边形CFDE是平行四边形;
综上所述,能画出3个平行四边形.
17.
【答案】
证明:∵ △ABF,△BCE都是等边△
∴ ∠FBA=∠EBC=60?,AB=BF=AF,BC=BE=EC
∴ ∠FBA?∠EBA=∠EBC?∠EBA
即∠FBE=∠CBA
又∵AB=BF,BC=BE
∴ △FBE?△ABC(SAS)
∴ AC=EF.
∵ △ACD得等边△
∴ AC=AD
∴ EF=AD
同理:AF=DE
∴ 四边形ADEF是平行四边形.
18.
【答案】
证明:连结AC,取AC的中点H,
连结NH,MH.
∵ N,H分别为BC,AC的中点,
∴ NH=//12AB?,
∴ ∠APM=∠HNM,
同理:MH=//12CD,
∴ ∠DQM=∠HMN.
∵ AB=CD,
∴ MH=NH,
∴ ∠HMN=∠HNM,
∴ ∠APM=∠DQM.
