浙江省东阳市南马高中2011-2012学年高二下学期期中考试数学(文)试题
文档属性
| 名称 | 浙江省东阳市南马高中2011-2012学年高二下学期期中考试数学(文)试题 |
|
|
| 格式 | zip | ||
| 文件大小 | 430.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-04-25 00:00:00 | ||
图片预览


文档简介
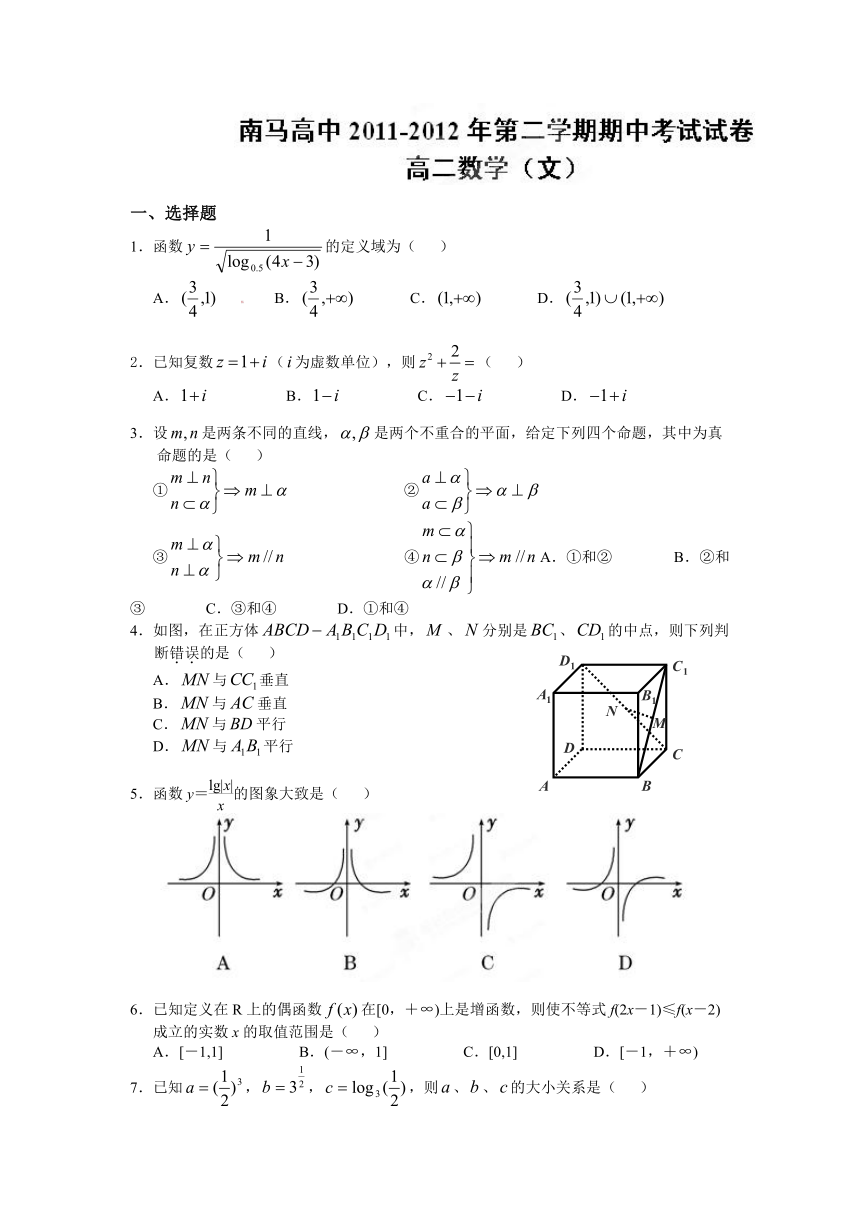
一、选择题
1.函数的定义域为( )
A. B. C. D.
2.已知复数(为虚数单位),则( )
A. B. C. D.
3.设是两条不同的直线,是两个不重合的平面,给定下列四个命题,其中为真
命题的是( )
① ②
③ ④A.①和② B.②和③ C.③和④ D.①和④
4.如图,在正方体中,、分别是、的中点,则下列判
断错误的是( )
A.与垂直
B.与垂直
C.与平行
D.与平行
5.函数y=的图象大致是( )
6.已知定义在R上的偶函数在[0,+∞)上是增函数,则使不等式f(2x-1)≤f(x-2)
成立的实数x的取值范围是( )
A.[-1,1] B.(-∞,1] C.[0,1] D.[-1,+∞)
7.已知,,,则、、的大小关系是( )
A. B. C. D.
8.若是方程的解,则属于区间( )
A.(,1) B.(,) C.(,) D.(0,)
9.点(0,1)到直线2x—y+2=0的距离为( )
A. B. C. D.
10.设定义在区间上的函数是奇函数(,且),则
的取值范围是( )
A. B. C. D.
二、填空题
11.双曲线的焦距是10,则实数m的值为 。
12.已知函数的图象如下所示:
给出下列四个命题:
(1)方程有且仅有6个根 (2)方程有且仅有3个根
(3)方程有且仅有5个根 (4)方程有且仅有4个根
其中正确命题是 。
13.若几何体的三视图如图所示,则此几何体的
体积为 。
14.一个骰子连续投2 次,点数和为4 的概率
。
15.曲线在点(0,1)处的切线
方程为 。
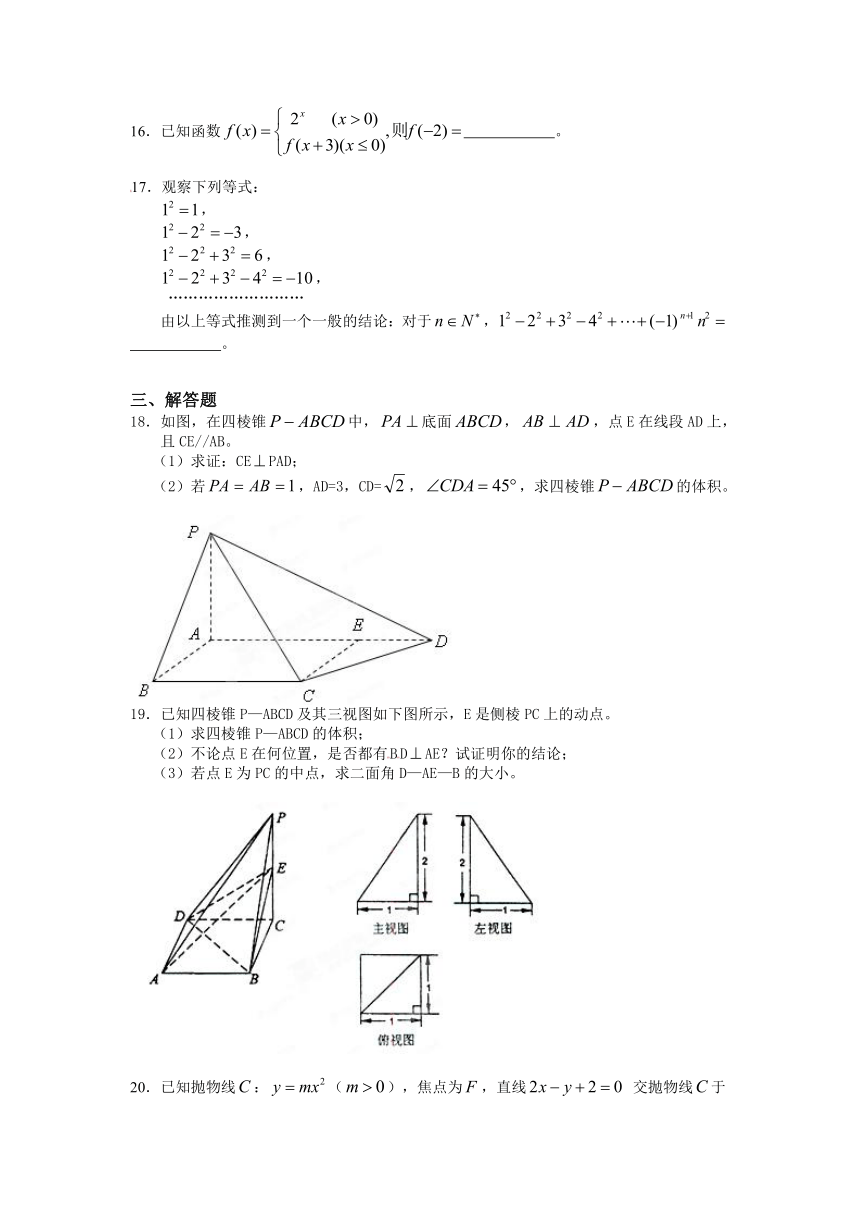
16.已知函数 。
17.观察下列等式:
,
,
,
,
………………………
由以上等式推测到一个一般的结论:对于,
。
三、解答题
18.如图,在四棱锥中,底面,,点E在线段AD上,且CE//AB。
(1)求证:CEPAD;
(2)若,AD=3,CD=,,求四棱锥的体积。
19.已知四棱锥P—ABCD及其三视图如下图所示,E是侧棱PC上的动点。
(1)求四棱锥P—ABCD的体积;
(2)不论点E在何位置,是否都有BDAE?试证明你的结论;
(3)若点E为PC的中点,求二面角D—AE—B的大小。
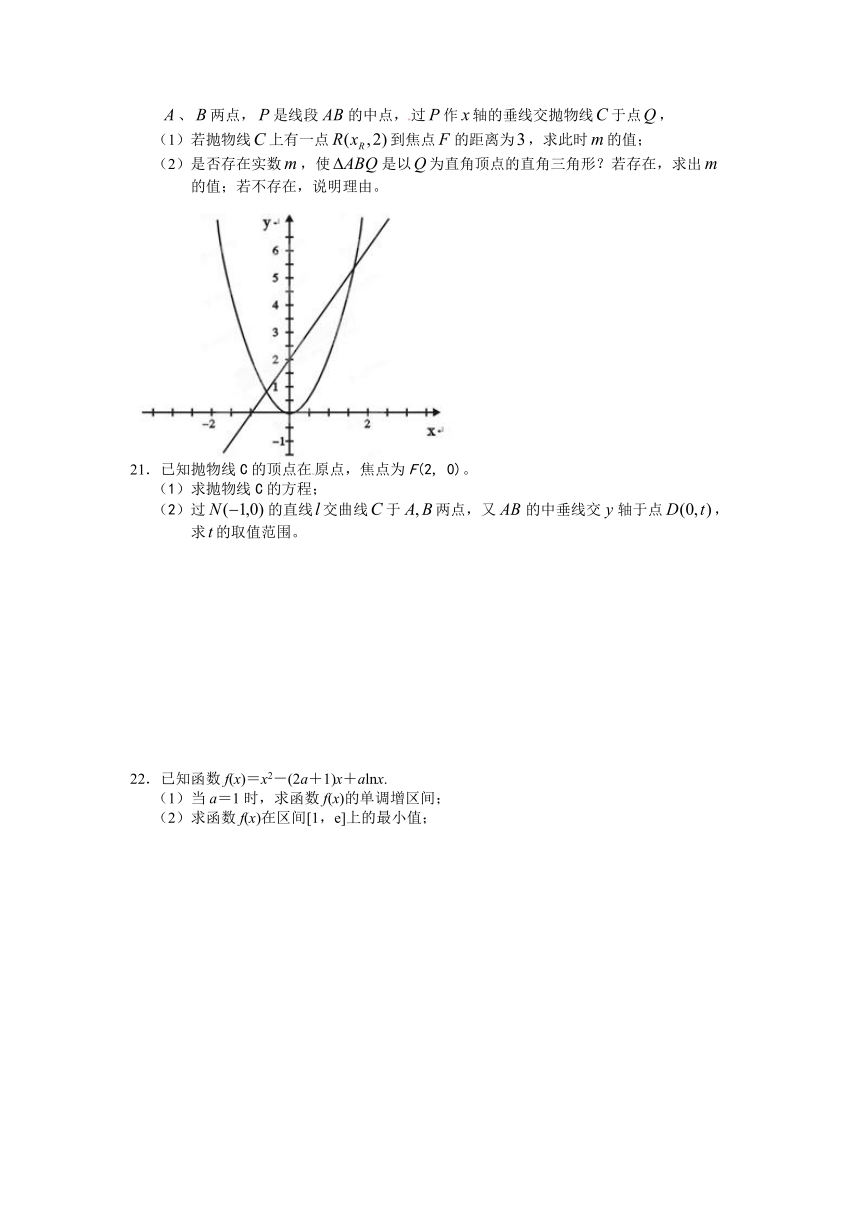
20.已知抛物线:(),焦点为,直线 交抛物线于
、两点,是线段的中点,过作轴的垂线交抛物线于点,
(1)若抛物线上有一点到焦点的距离为,求此时的值;
(2)是否存在实数,使是以为直角顶点的直角三角形?若存在,求出
的值;若不存在,说明理由。
21.已知抛物线C的顶点在原点,焦点为F(2, 0)。
(1)求抛物线C的方程;
(2)过的直线交曲线于两点,又的中垂线交轴于点,
求的取值范围。
22.已知函数f(x)=x2-(2a+1)x+alnx.
(1)当a=1时,求函数f(x)的单调增区间;
(2)求函数f(x)在区间[1,e]上的最小值;
1.A
解析:由log0.5(4x-3)>0且4x-3>0得0<4x-3<1,<x<1.
即函数的定义域是(,1).
7.B
8.B
9.A
10.B
11.16
12.(1)(3)(4)
13.
14.
15.y=3x+1
16.2
17.
18.
19.
(3)解:
20.20.解:(1)抛物线的焦点,---------------------------------------------------2分
,得。----------------------------------6分
(或利用得
,或(舍去))
(2)联立方程,消去得,设,
则(),-----------------------------------------------------------------------8分
是线段的中点,,即,
,-----------------------------------------------------------------------------------10分
得,
若存在实数,使是以为直角顶点的直角三角形,则,-----11分
即,结合()化简得,
即,或(舍去),
存在实数,使是以为直角顶点的直角三角形。----------------------------15分
21.解: .解:(1)设抛物线方程为,则,
所以,抛物线的方程是. …………………4分
(2)直线的方程是,联立消去得,…6分
显然,由,得. ……………8分
由韦达定理得,,
所以,则中点坐标是,……10分
由 可得 ,
所以,,令,则,其中,…………12分
因为,所以函数是在上增函数.
所以,的取值范围是. ……………………15分
22.解:(1)当a=1时,f(x)=x2-3x+lnx,定义域为(0,+∞),
f′(x)=2x-3+==.
令f′(x)=0,得x=1或x=.
x (0,) (,1) 1 (1,+∞)
f′(x) + 0 - 0 +
f(x) ? 极大值 ? 极小值 ?
所以函数f(x)的单调增区间为(0,),(1,+∞).
(2)f′(x)=2x-(2a+1)+==,令f′(x)=0,得x=a或x=.
当a≤时,f(x)在[,+∞)上单调增,所以f(x)在区间[1,e]上单调增;
当综上,当a≤1时,f(x)min=f(1)=-2a;
当1x (1,a) a (a,e)
f′(x) - 0 +
f(x) ? a(lna-a-1) ?
所以f(x)min=f(a)=a(lna-a-1);
当a≥e时,f(x)在(0,],[a,+∞)上单调增,在(,a)上单调减,所以在[1,e]上单调减.
所以f(x)min=f(e)=e2-(2a+1)e+a.
(第13题)
1.函数的定义域为( )
A. B. C. D.
2.已知复数(为虚数单位),则( )
A. B. C. D.
3.设是两条不同的直线,是两个不重合的平面,给定下列四个命题,其中为真
命题的是( )
① ②
③ ④A.①和② B.②和③ C.③和④ D.①和④
4.如图,在正方体中,、分别是、的中点,则下列判
断错误的是( )
A.与垂直
B.与垂直
C.与平行
D.与平行
5.函数y=的图象大致是( )
6.已知定义在R上的偶函数在[0,+∞)上是增函数,则使不等式f(2x-1)≤f(x-2)
成立的实数x的取值范围是( )
A.[-1,1] B.(-∞,1] C.[0,1] D.[-1,+∞)
7.已知,,,则、、的大小关系是( )
A. B. C. D.
8.若是方程的解,则属于区间( )
A.(,1) B.(,) C.(,) D.(0,)
9.点(0,1)到直线2x—y+2=0的距离为( )
A. B. C. D.
10.设定义在区间上的函数是奇函数(,且),则
的取值范围是( )
A. B. C. D.
二、填空题
11.双曲线的焦距是10,则实数m的值为 。
12.已知函数的图象如下所示:
给出下列四个命题:
(1)方程有且仅有6个根 (2)方程有且仅有3个根
(3)方程有且仅有5个根 (4)方程有且仅有4个根
其中正确命题是 。
13.若几何体的三视图如图所示,则此几何体的
体积为 。
14.一个骰子连续投2 次,点数和为4 的概率
。
15.曲线在点(0,1)处的切线
方程为 。
16.已知函数 。
17.观察下列等式:
,
,
,
,
………………………
由以上等式推测到一个一般的结论:对于,
。
三、解答题
18.如图,在四棱锥中,底面,,点E在线段AD上,且CE//AB。
(1)求证:CEPAD;
(2)若,AD=3,CD=,,求四棱锥的体积。
19.已知四棱锥P—ABCD及其三视图如下图所示,E是侧棱PC上的动点。
(1)求四棱锥P—ABCD的体积;
(2)不论点E在何位置,是否都有BDAE?试证明你的结论;
(3)若点E为PC的中点,求二面角D—AE—B的大小。
20.已知抛物线:(),焦点为,直线 交抛物线于
、两点,是线段的中点,过作轴的垂线交抛物线于点,
(1)若抛物线上有一点到焦点的距离为,求此时的值;
(2)是否存在实数,使是以为直角顶点的直角三角形?若存在,求出
的值;若不存在,说明理由。
21.已知抛物线C的顶点在原点,焦点为F(2, 0)。
(1)求抛物线C的方程;
(2)过的直线交曲线于两点,又的中垂线交轴于点,
求的取值范围。
22.已知函数f(x)=x2-(2a+1)x+alnx.
(1)当a=1时,求函数f(x)的单调增区间;
(2)求函数f(x)在区间[1,e]上的最小值;
1.A
解析:由log0.5(4x-3)>0且4x-3>0得0<4x-3<1,<x<1.
即函数的定义域是(,1).
7.B
8.B
9.A
10.B
11.16
12.(1)(3)(4)
13.
14.
15.y=3x+1
16.2
17.
18.
19.
(3)解:
20.20.解:(1)抛物线的焦点,---------------------------------------------------2分
,得。----------------------------------6分
(或利用得
,或(舍去))
(2)联立方程,消去得,设,
则(),-----------------------------------------------------------------------8分
是线段的中点,,即,
,-----------------------------------------------------------------------------------10分
得,
若存在实数,使是以为直角顶点的直角三角形,则,-----11分
即,结合()化简得,
即,或(舍去),
存在实数,使是以为直角顶点的直角三角形。----------------------------15分
21.解: .解:(1)设抛物线方程为,则,
所以,抛物线的方程是. …………………4分
(2)直线的方程是,联立消去得,…6分
显然,由,得. ……………8分
由韦达定理得,,
所以,则中点坐标是,……10分
由 可得 ,
所以,,令,则,其中,…………12分
因为,所以函数是在上增函数.
所以,的取值范围是. ……………………15分
22.解:(1)当a=1时,f(x)=x2-3x+lnx,定义域为(0,+∞),
f′(x)=2x-3+==.
令f′(x)=0,得x=1或x=.
x (0,) (,1) 1 (1,+∞)
f′(x) + 0 - 0 +
f(x) ? 极大值 ? 极小值 ?
所以函数f(x)的单调增区间为(0,),(1,+∞).
(2)f′(x)=2x-(2a+1)+==,令f′(x)=0,得x=a或x=.
当a≤时,f(x)在[,+∞)上单调增,所以f(x)在区间[1,e]上单调增;
当
当1
f′(x) - 0 +
f(x) ? a(lna-a-1) ?
所以f(x)min=f(a)=a(lna-a-1);
当a≥e时,f(x)在(0,],[a,+∞)上单调增,在(,a)上单调减,所以在[1,e]上单调减.
所以f(x)min=f(e)=e2-(2a+1)e+a.
(第13题)
同课章节目录
