湖南省永州市第五中学2011-2012学年高二下学期第一学段考试数学试题(无答案)
文档属性
| 名称 | 湖南省永州市第五中学2011-2012学年高二下学期第一学段考试数学试题(无答案) |  | |
| 格式 | zip | ||
| 文件大小 | 131.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-04-25 15:44:00 | ||
图片预览
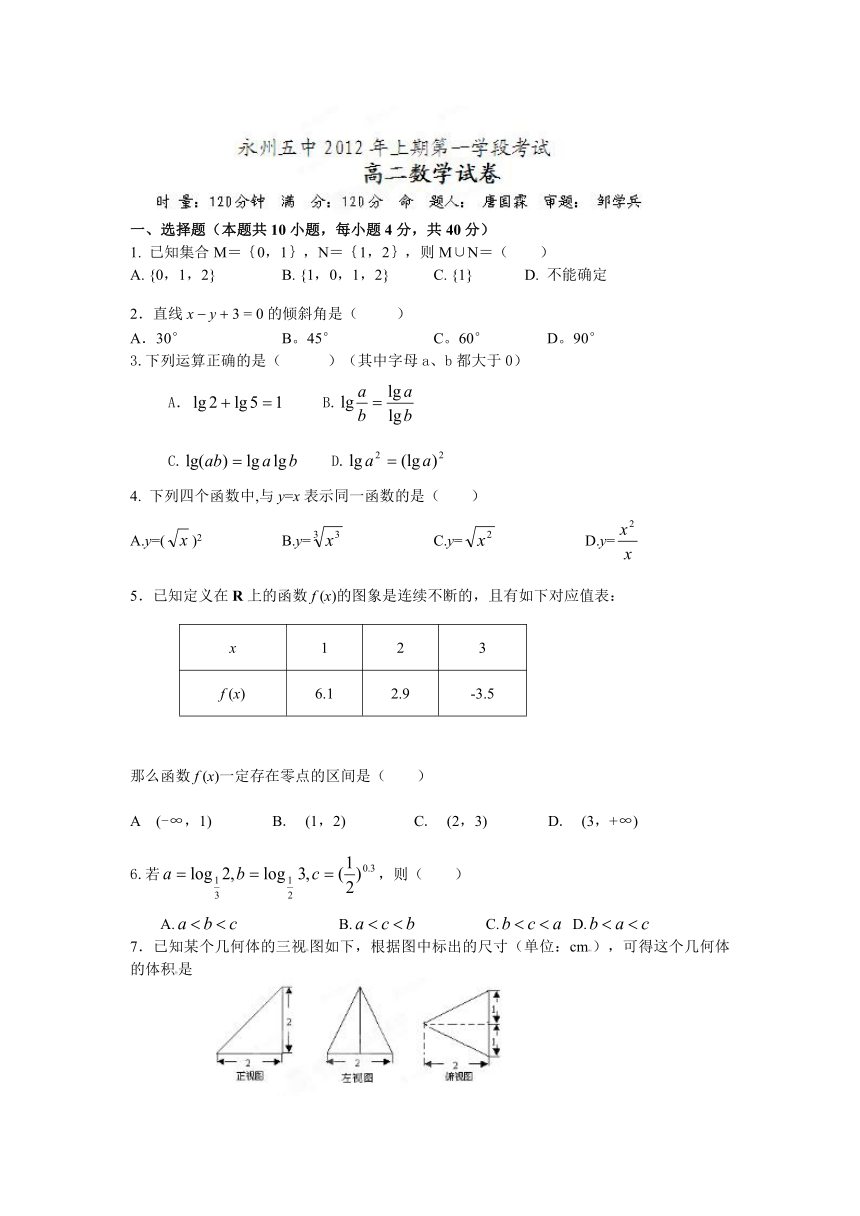

文档简介
一、选择题(本题共10小题,每小题4分,共40分)
1. 已知集合M={0,1},N={1,2},则M∪N=( )
A. {0,1,2} B. {1,0,1,2} C. {1} D. 不能确定
2.直线x y 3 = 0的倾斜角是( )
A.30° B。45° C。60° D。90°
3.下列运算正确的是( )(其中字母a、b都大于0)
A. B.
C. D.
4. 下列四个函数中,与y=x表示同一函数的是( )
A.y=()2 B.y= C.y= D.y=
5.已知定义在R上的函数f (x)的图象是连续不断的,且有如下对应值表:
x 1 2 3
f (x) 6.1 2.9 -3.5
那么函数f (x)一定存在零点的区间是( )
A (-∞,1) B. (1,2) C. (2,3) D. (3,+∞)
6.若,则( )
A. B. C. D.
7.已知某个几何体的三视图如下,根据图中标出的尺寸(单位:cm),可得这个几何体的体积是
A. B. C. D.
8.已知函数在区间内单调递减,则a的取值范围( )
A. B. C. D.
9、在右图的正方体中,M、N分别为棱BC和棱CC1的中点,则异面直线AC和MN所成的角为( )
A.30° B.45° C.60° D.90°
10、若直线与圆相交于两点,且(其中为原点),则的值为( )
A.或 B. C.或 D.
二、填空题(本题共5小题,每小题4分,共20分)
11.函数在区间[3,6]上的最大值是________;最小值是__________;
12.已知直线与直线 平行,则 .
13.已知幂函数的图象过,则=_________
14.已知,若,则的值是_________
15.已知l⊥α,mβ,则下面四个命题:
①α∥β则l⊥m ②α⊥β则l∥m ③l∥m则α⊥β ④l⊥m则α∥β
其中正确的是___ _____
三、解答题(本题共6小题,共60分,解答应写出文字说明、证明过程或演算步骤)
16.(本题满分10分)
已知直线:,:,求:
(1)直线与的交点的坐标;(2)过点且与垂直的直线方程.
17计算:(1)
(2)
18(本题满分12分)、如图,四棱锥P-ABCD中,底面ABCD为矩形,PD⊥平面ABCD,点E、F分别是AB和PC的中点.
(1) 求证:AB⊥平面PAD;
(2) 求证:EF//平面PAD.
19(本题满分13分)、设。
(1)证明:f(x)在(0,1)上是减函数.
(2)当时,求函数f(x)的值域。
20.(本题满分10分)通过研究学生的学习行为,专家发现,学生的注意力随着老师讲课时间的变化而变化,讲课开始时,学生的兴趣激增,中间一段时间,学生保持较理想的状态,随后学生的注意力开始分散,设表示学生注意力随时间(分钟)的变化规律(越大,表明学生注意力越集中),经实验分析得知
(Ⅰ) 讲课开始多少分钟,学生的注意力最集中?能持续多少分钟?
(Ⅱ) 讲课开始后5分钟与讲课开始后25分钟比较,何时学生的注意力更集中?
21.(本题满分10分)
已知圆,
(Ⅰ)若直线过定点(1,0),且与圆相切,求的方程;
(Ⅱ) 若圆的半径为3,圆心在直线:上,且与圆外切,求圆的方程.
1. 已知集合M={0,1},N={1,2},则M∪N=( )
A. {0,1,2} B. {1,0,1,2} C. {1} D. 不能确定
2.直线x y 3 = 0的倾斜角是( )
A.30° B。45° C。60° D。90°
3.下列运算正确的是( )(其中字母a、b都大于0)
A. B.
C. D.
4. 下列四个函数中,与y=x表示同一函数的是( )
A.y=()2 B.y= C.y= D.y=
5.已知定义在R上的函数f (x)的图象是连续不断的,且有如下对应值表:
x 1 2 3
f (x) 6.1 2.9 -3.5
那么函数f (x)一定存在零点的区间是( )
A (-∞,1) B. (1,2) C. (2,3) D. (3,+∞)
6.若,则( )
A. B. C. D.
7.已知某个几何体的三视图如下,根据图中标出的尺寸(单位:cm),可得这个几何体的体积是
A. B. C. D.
8.已知函数在区间内单调递减,则a的取值范围( )
A. B. C. D.
9、在右图的正方体中,M、N分别为棱BC和棱CC1的中点,则异面直线AC和MN所成的角为( )
A.30° B.45° C.60° D.90°
10、若直线与圆相交于两点,且(其中为原点),则的值为( )
A.或 B. C.或 D.
二、填空题(本题共5小题,每小题4分,共20分)
11.函数在区间[3,6]上的最大值是________;最小值是__________;
12.已知直线与直线 平行,则 .
13.已知幂函数的图象过,则=_________
14.已知,若,则的值是_________
15.已知l⊥α,mβ,则下面四个命题:
①α∥β则l⊥m ②α⊥β则l∥m ③l∥m则α⊥β ④l⊥m则α∥β
其中正确的是___ _____
三、解答题(本题共6小题,共60分,解答应写出文字说明、证明过程或演算步骤)
16.(本题满分10分)
已知直线:,:,求:
(1)直线与的交点的坐标;(2)过点且与垂直的直线方程.
17计算:(1)
(2)
18(本题满分12分)、如图,四棱锥P-ABCD中,底面ABCD为矩形,PD⊥平面ABCD,点E、F分别是AB和PC的中点.
(1) 求证:AB⊥平面PAD;
(2) 求证:EF//平面PAD.
19(本题满分13分)、设。
(1)证明:f(x)在(0,1)上是减函数.
(2)当时,求函数f(x)的值域。
20.(本题满分10分)通过研究学生的学习行为,专家发现,学生的注意力随着老师讲课时间的变化而变化,讲课开始时,学生的兴趣激增,中间一段时间,学生保持较理想的状态,随后学生的注意力开始分散,设表示学生注意力随时间(分钟)的变化规律(越大,表明学生注意力越集中),经实验分析得知
(Ⅰ) 讲课开始多少分钟,学生的注意力最集中?能持续多少分钟?
(Ⅱ) 讲课开始后5分钟与讲课开始后25分钟比较,何时学生的注意力更集中?
21.(本题满分10分)
已知圆,
(Ⅰ)若直线过定点(1,0),且与圆相切,求的方程;
(Ⅱ) 若圆的半径为3,圆心在直线:上,且与圆外切,求圆的方程.
同课章节目录
