2020-2021学年安徽省合肥市庐阳区七年级(下)期末数学试卷(Word版 含解析)
文档属性
| 名称 | 2020-2021学年安徽省合肥市庐阳区七年级(下)期末数学试卷(Word版 含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 581.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-07 05:35:02 | ||
图片预览



文档简介
2020-2021学年安徽省合肥市庐阳区七年级(下)期末数学试卷
一、选择题(共10小题).
1.16的算术平方根是( )
A.﹣4 B.4 C. D.
2.下列运算正确的是( )
A.a+2a=3a2 B.(a2)3=a5 C.a3?a4=a12 D.(﹣3a)2=9a2
3.如果分式的值为0,那么x的值是( )
A.x=3 B.x=±3 C.x≠3 D.x=﹣3
4.如图,圆的直径为1个单位长度,该圆上的点A与数轴上表示1的点重合,将该圆沿数轴向左滚动1周,点A到达A′的位置,则点A′表示的数是( )
A.π﹣1 B.﹣π+1 C.﹣π﹣1 D.π﹣1或﹣π﹣1
5.下列从左到右变形正确的是( )
A.= B.=
C.(a﹣b)2=a2﹣b2 D.(a﹣2)(a+3)=a2+a﹣6
6.若两个连续整数x,y满足x<<y,则x+y的值是( )
A.5 B.6 C.7 D.8
7.如果m2+m=5,那么代数式m(m﹣2)+(m+2)2的值为( )
A.14 B.9 C.﹣1 D.﹣6
8.若不等式(m+3)x>2m+6的解集为x<2,则m的取值范围为( )
A.m>0 B.m>﹣3 C.m<0 D.m<﹣3
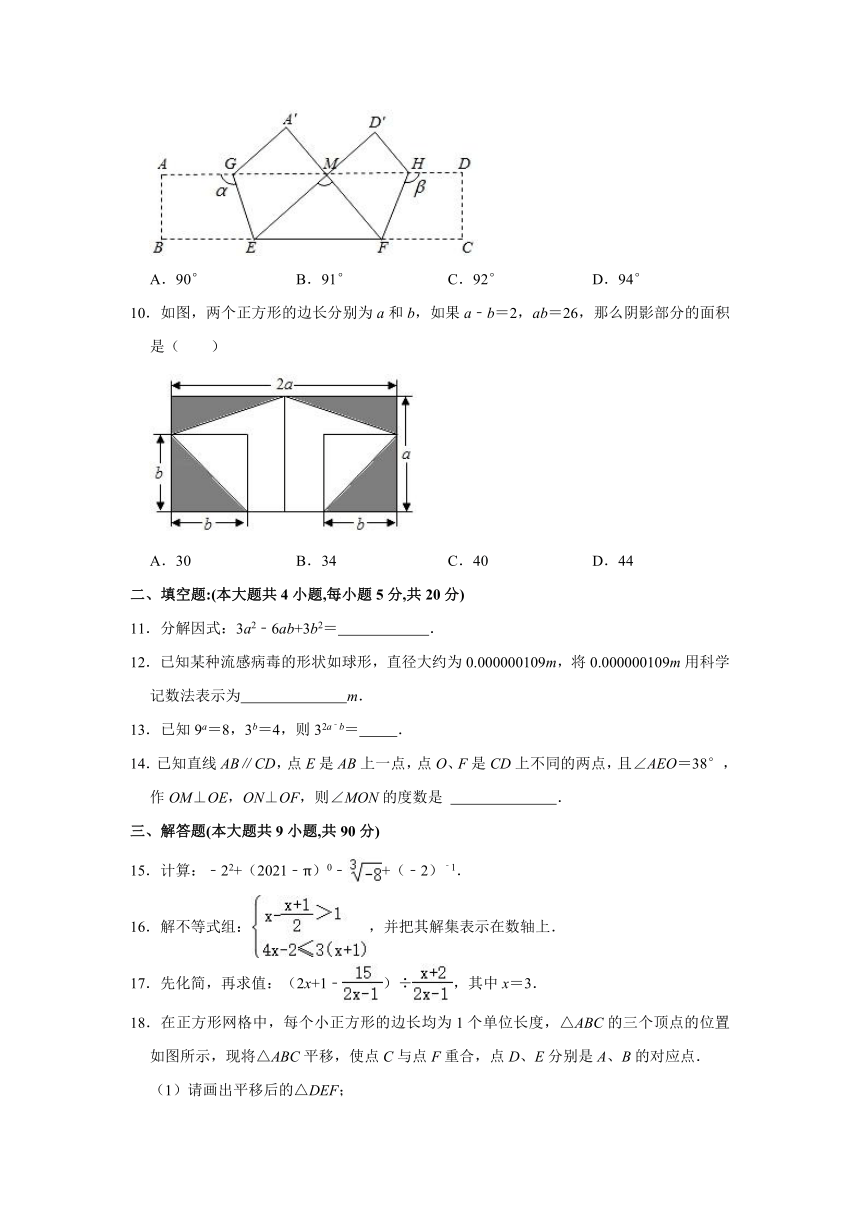
9.如图,已知长方形纸片ABCD,点E、F在BC边上,点G、H在AD边上,分别沿EG、FH折叠,使点B和点C都落在点M处,若α+β=224°,则∠EMF的度数为( )
A.90° B.91° C.92° D.94°
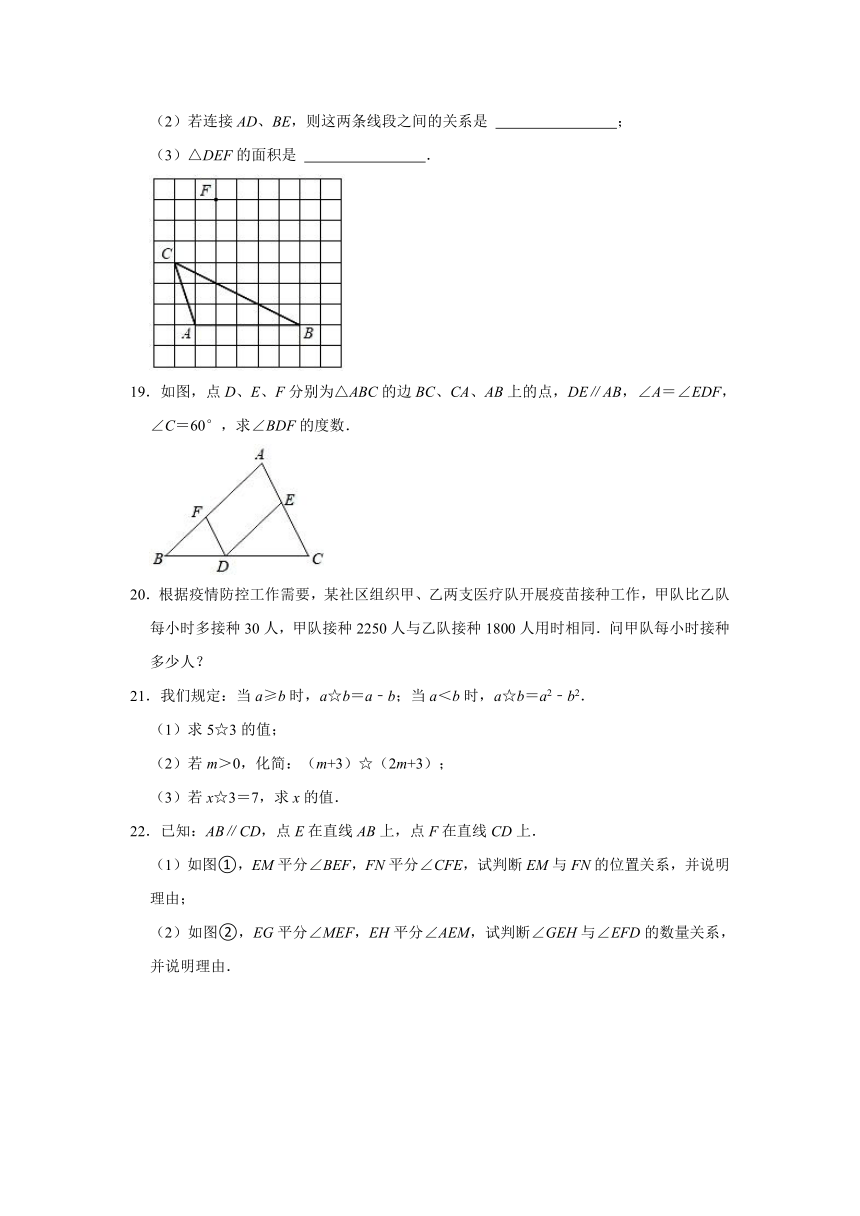
10.如图,两个正方形的边长分别为a和b,如果a﹣b=2,ab=26,那么阴影部分的面积是( )
A.30 B.34 C.40 D.44
二、填空题:(本大题共4小题,每小题5分,共20分)
11.分解因式:3a2﹣6ab+3b2= .
12.已知某种流感病毒的形状如球形,直径大约为0.000000109m,将0.000000109m用科学记数法表示为 m.
13.已知9a=8,3b=4,则32a﹣b= .
14.已知直线AB∥CD,点E是AB上一点,点O、F是CD上不同的两点,且∠AEO=38°,作OM⊥OE,ON⊥OF,则∠MON的度数是 .
三、解答题(本大题共9小题,共90分)
15.计算:﹣22+(2021﹣π)0﹣+(﹣2)﹣1.
16.解不等式组:,并把其解集表示在数轴上.
17.先化简,再求值:(2x+1﹣)÷,其中x=3.
18.在正方形网格中,每个小正方形的边长均为1个单位长度,△ABC的三个顶点的位置如图所示,现将△ABC平移,使点C与点F重合,点D、E分别是A、B的对应点.
(1)请画出平移后的△DEF;
(2)若连接AD、BE,则这两条线段之间的关系是 ;
(3)△DEF的面积是 .
19.如图,点D、E、F分别为△ABC的边BC、CA、AB上的点,DE∥AB,∠A=∠EDF,∠C=60°,求∠BDF的度数.
20.根据疫情防控工作需要,某社区组织甲、乙两支医疗队开展疫苗接种工作,甲队比乙队每小时多接种30人,甲队接种2250人与乙队接种1800人用时相同.问甲队每小时接种多少人?
21.我们规定:当a≥b时,a☆b=a﹣b;当a<b时,a☆b=a2﹣b2.
(1)求5☆3的值;
(2)若m>0,化简:(m+3)☆(2m+3);
(3)若x☆3=7,求x的值.
22.已知:AB∥CD,点E在直线AB上,点F在直线CD上.
(1)如图①,EM平分∠BEF,FN平分∠CFE,试判断EM与FN的位置关系,并说明理由;
(2)如图②,EG平分∠MEF,EH平分∠AEM,试判断∠GEH与∠EFD的数量关系,并说明理由.
23.随着中国“十四五”规划的推进和国家政策的刺激,新能源板块成为重点发展的领域之一.某品牌汽车生产厂家生产了一批油电混合动力汽车和纯电动汽车,每辆油电混合动力汽车比纯电动汽车生产成本多1万元,现生产2000辆油电混合动力汽车与1600辆纯电动汽车共耗资21800万元.两款汽车的部分对比参数如表:
汽车类型 生产成本(万元/辆) 预售价(万元/辆) 补贴(万元/辆)
油电混合动力汽车
8.8 1.2
纯电动汽车
6.6 1.5
(1)每辆油电混合动力汽车的生产成本是多少万元?
(2)为扶持新能源汽车发展,消费者可享受新能源汽车的政府补贴.某上市公司准备用120万资金采购该品牌的新能源汽车共20辆,且油电混合动力汽车不少于5辆,该公司有几种购买方案?请为公司选择一种满足要求的最省钱的方案.
参考答案
一、选择题(本大题共10小题,每小题4分,共40分)
1.16的算术平方根是( )
A.﹣4 B.4 C. D.
解:由42=16,得
=4,故B符合题意,
故选:B.
2.下列运算正确的是( )
A.a+2a=3a2 B.(a2)3=a5 C.a3?a4=a12 D.(﹣3a)2=9a2
解:A.a+2a=3a,故此选项不符合题意;
B.(a2)3=a6,故此选项不符合题意;
C.a3?a4=a7,故此选项不符合题意;
D.(﹣3a)2=9a2,正确,故此选项符合题意,
故选:D.
3.如果分式的值为0,那么x的值是( )
A.x=3 B.x=±3 C.x≠3 D.x=﹣3
解:由题意得:x﹣3=0且x+3≠0,
解得:x=3,
故选:A.
4.如图,圆的直径为1个单位长度,该圆上的点A与数轴上表示1的点重合,将该圆沿数轴向左滚动1周,点A到达A′的位置,则点A′表示的数是( )
A.π﹣1 B.﹣π+1 C.﹣π﹣1 D.π﹣1或﹣π﹣1
解:∵圆的直径为1个单位长度,
∴此圆的周长=π,
∴当圆向左滚动时点A′表示的数是﹣π+1;
故选:B.
5.下列从左到右变形正确的是( )
A.= B.=
C.(a﹣b)2=a2﹣b2 D.(a﹣2)(a+3)=a2+a﹣6
解:A、≠,原变形错误,故此选项不符合题意.
B、当m=0时,此时无意义,原变形错误,故此选项不符合题意.
C、(a﹣b)2=a2﹣2ab+b2,原变形错误,故此选项不符合题意.
D、(a﹣2)(a+3)=a2+a﹣6,原变形正确,故此选项符合题意.
故选:D.
6.若两个连续整数x,y满足x<<y,则x+y的值是( )
A.5 B.6 C.7 D.8
解:∵9<10<16,
∴,
∴3<<4,
∴x=3,y=4,
∴x+y的值是3+4=7,
故选:C.
7.如果m2+m=5,那么代数式m(m﹣2)+(m+2)2的值为( )
A.14 B.9 C.﹣1 D.﹣6
解:m(m﹣2)+(m+2)2
=m2﹣2m+m2+4m+4
=2m2+2m+4.
当m2+m=5时,原式=2(m2+m)+4=2×5+4=10+4=14.
故选:A.
8.若不等式(m+3)x>2m+6的解集为x<2,则m的取值范围为( )
A.m>0 B.m>﹣3 C.m<0 D.m<﹣3
解:∵(m+3)x>2m+6的解集为x<2,
∴m+3<0,
解得m<﹣3,
故选:D.
9.如图,已知长方形纸片ABCD,点E、F在BC边上,点G、H在AD边上,分别沿EG、FH折叠,使点B和点C都落在点M处,若α+β=224°,则∠EMF的度数为( )
A.90° B.91° C.92° D.94°
解:∵四边形ABCD是长方形,
∴AD∥BC,
∴∠BEG+α=180°,∠CFH+β=180°,
∴∠BEG=180°﹣α,∠CFH=180°﹣β,
∵α+β=224°,
∴∠BEG+∠CFH=360°﹣(α+β)=136°,
由折叠可知:
∠BEG=∠GEM,∠CFH=∠HFM,
∴∠BEM+∠CFM=2(∠BEG+∠CFH)=272°,
∴∠MEF+∠MFE=360°﹣(∠BEM+∠CFM)=360°﹣272°=88°,
∴∠EMF=180°﹣(∠MEF+∠MFE)=92°,
故选:C.
10.如图,两个正方形的边长分别为a和b,如果a﹣b=2,ab=26,那么阴影部分的面积是( )
A.30 B.34 C.40 D.44
解:如图,
∵a﹣b=2,ab=26,
∴a2﹣2ab+b2=4,
∴a2+b2=4+2ab=4+52=56,
阴影部分的面积=S△ABC+S△CDM+S△AEF+S△GHM
=2×(a﹣b)×a+2×b×b
=a(a﹣b)+b2
=a2+b2﹣ab
=56﹣26
=30.
故选:A.
二、填空题:(本大题共4小题,每小题5分,共20分)
11.分解因式:3a2﹣6ab+3b2= 3(a﹣b)2 .
解:3a2﹣6ab+3b2
=3(a2﹣2ab+b2)
=3(a﹣b)2.
故答案为:3(a﹣b)2.
12.已知某种流感病毒的形状如球形,直径大约为0.000000109m,将0.000000109m用科学记数法表示为 1.09×10﹣7 m.
解:将0.000000109m用科学记数法表示为1.09×10﹣7m.
故答案是:1.09×10﹣7.
13.已知9a=8,3b=4,则32a﹣b= 2 .
解:原式=32a÷3b=(32)a÷3b=9a÷3b=8÷4=2,
故答案为:2.
14.已知直线AB∥CD,点E是AB上一点,点O、F是CD上不同的两点,且∠AEO=38°,作OM⊥OE,ON⊥OF,则∠MON的度数是 38°或者142° .
解:根据题意有图1、图2两种情况:
图1中,
∵AB∥CD,
∴∠AEO=∠DO=38°,
∵MO⊥OE,ON⊥OF,
∴∠MOE=∠NOF=90°,
∴∠MON=90°﹣(90°﹣38°)=38°;
图2中,
∵AB∥CD,
∴∠AEO=∠DOE=38°,
∵MO⊥OE,ON⊥OF,
∴∠MOE=∠NOF=90°,
∴∠MON=180°﹣38°=142°
综上,∠MON的度数为38°或者142°.
故答案为:38°或者142°.
三、解答题(本大题共9小题,共90分)
15.计算:﹣22+(2021﹣π)0﹣+(﹣2)﹣1.
【解答】原式=﹣4+1﹣(﹣2)+(﹣)
=﹣4+1+2﹣
=﹣.
16.解不等式组:,并把其解集表示在数轴上.
解:,
由①得,x>3,
由②得,x≤5,
故此不等式组的解集为:3<x≤5.
在数轴上表示为:
.
17.先化简,再求值:(2x+1﹣)÷,其中x=3.
解:原式=[﹣]÷
=?
=
=
=4x+8,
当x=3时,
原式=4×3+8
=20.
18.在正方形网格中,每个小正方形的边长均为1个单位长度,△ABC的三个顶点的位置如图所示,现将△ABC平移,使点C与点F重合,点D、E分别是A、B的对应点.
(1)请画出平移后的△DEF;
(2)若连接AD、BE,则这两条线段之间的关系是 AD∥BE,AD=BE ;
(3)△DEF的面积是 .
解:(1)如图,△DEF即为所求.
(2)观察图形可知AD∥BE,AD=BE.
故答案为:AD∥BE,AD=BE.
(3)S△DEF=×5×3=,
故答案为:.
19.如图,点D、E、F分别为△ABC的边BC、CA、AB上的点,DE∥AB,∠A=∠EDF,∠C=60°,求∠BDF的度数.
解:∵DE∥AB,
∴∠A=∠CED,
∵∠A=∠EDF,
∴∠EDF=∠CED,
∴DF∥AC,
∴∠BDF=∠C,
∵∠C=60°,
∴∠BDF=60°.
20.根据疫情防控工作需要,某社区组织甲、乙两支医疗队开展疫苗接种工作,甲队比乙队每小时多接种30人,甲队接种2250人与乙队接种1800人用时相同.问甲队每小时接种多少人?
解:设甲队每小时接种x人,则乙队每小时接种(x﹣30)人,
依题意得:=,
解得:x=150,
经检验,x=150是原方程的解,且符合题意.
答:甲队每小时接种150人.
21.我们规定:当a≥b时,a☆b=a﹣b;当a<b时,a☆b=a2﹣b2.
(1)求5☆3的值;
(2)若m>0,化简:(m+3)☆(2m+3);
(3)若x☆3=7,求x的值.
解:(1)∵5>3,
∴原式=5﹣3=2;
(2)当m>0时,
∵m+3﹣(2m+3)
=m+3﹣2m﹣3
=﹣m<0,
∴m+3<2m+3,
∴原式=(m+3)2﹣(2m+3)2
=(m+3+2m+3)[m+3﹣(2m+3)]
=(m+3+2m+3)(﹣m)
=(3m+6)(﹣m)
=﹣3m2﹣6m;
(3)当x≥3时,x﹣3=7,
解得:x=10;
当x<3时,x2﹣32=7,
解得:x=±4,
∵x<3,
∴x=4不符合题意,
∴x=﹣4;
综上所述,x=10或﹣4.
22.已知:AB∥CD,点E在直线AB上,点F在直线CD上.
(1)如图①,EM平分∠BEF,FN平分∠CFE,试判断EM与FN的位置关系,并说明理由;
(2)如图②,EG平分∠MEF,EH平分∠AEM,试判断∠GEH与∠EFD的数量关系,并说明理由.
解:(1)如图①位置关系是:EM∥FN,理由:
∵AB∥CD,
∴∠BEF=∠CFE,
∵EM平分∠BEF,FN平分∠CFE,
∴∠MEF=∠BEF,∠NFE=∠CFE,
∴∠MEF=∠NFE,
∴EM∥FN;
(2)如图②,∠EFD=2∠GEH,理由:
∵EG平分∠MEF,
∴∠MEG=∠GEH+∠HEF,
∵EH平分∠AEM,
∴∠MEG+∠GEH=∠AEF+∠HEF,
∴∠AEF=2∠GEH,
∵AB∥CD,
∴∠AEF=∠EFD,
∴∠EFD=2∠GEH.
23.随着中国“十四五”规划的推进和国家政策的刺激,新能源板块成为重点发展的领域之一.某品牌汽车生产厂家生产了一批油电混合动力汽车和纯电动汽车,每辆油电混合动力汽车比纯电动汽车生产成本多1万元,现生产2000辆油电混合动力汽车与1600辆纯电动汽车共耗资21800万元.两款汽车的部分对比参数如表:
汽车类型 生产成本(万元/辆) 预售价(万元/辆) 补贴(万元/辆)
油电混合动力汽车
8.8 1.2
纯电动汽车
6.6 1.5
(1)每辆油电混合动力汽车的生产成本是多少万元?
(2)为扶持新能源汽车发展,消费者可享受新能源汽车的政府补贴.某上市公司准备用120万资金采购该品牌的新能源汽车共20辆,且油电混合动力汽车不少于5辆,该公司有几种购买方案?请为公司选择一种满足要求的最省钱的方案.
解:(1)设每辆油电混合动力汽车的生产成本是x万元,则每辆纯电动汽车的生产成本是(x﹣1)万元,
依题意得:2000x+1600(x﹣1)=21800,
解得:x=6.5,
答:每辆油电混合动力汽车的生产成本是6.5万元.
(2)设购进油电混合动力汽车m辆,则购进纯电动汽车(20﹣m)辆,
依题意得:,
解得:5≤m≤,
又∵m为整数,
∴m可以取5,6,7,
∴该公司共有3种购买方案,
方案1:购进油电混合动力汽车5辆,纯电动汽车15辆,所需费用为(8.8﹣1.2)×5+(6.6﹣1.5)×15=114.5(万元);
方案2:购进油电混合动力汽车6辆,纯电动汽车14辆,所需费用为(8.8﹣1.2)×6+(6.6﹣1.5)×14=117(万元);
方案3:购进油电混合动力汽车7辆,纯电动汽车13辆,所需费用为(8.8﹣1.2)×7+(6.6﹣1.5)×13=119.5(万元).
∵114.5<117<119.5,
∴最省钱的方案为:购进油电混合动力汽车5辆,纯电动汽车15辆.
一、选择题(共10小题).
1.16的算术平方根是( )
A.﹣4 B.4 C. D.
2.下列运算正确的是( )
A.a+2a=3a2 B.(a2)3=a5 C.a3?a4=a12 D.(﹣3a)2=9a2
3.如果分式的值为0,那么x的值是( )
A.x=3 B.x=±3 C.x≠3 D.x=﹣3
4.如图,圆的直径为1个单位长度,该圆上的点A与数轴上表示1的点重合,将该圆沿数轴向左滚动1周,点A到达A′的位置,则点A′表示的数是( )
A.π﹣1 B.﹣π+1 C.﹣π﹣1 D.π﹣1或﹣π﹣1
5.下列从左到右变形正确的是( )
A.= B.=
C.(a﹣b)2=a2﹣b2 D.(a﹣2)(a+3)=a2+a﹣6
6.若两个连续整数x,y满足x<<y,则x+y的值是( )
A.5 B.6 C.7 D.8
7.如果m2+m=5,那么代数式m(m﹣2)+(m+2)2的值为( )
A.14 B.9 C.﹣1 D.﹣6
8.若不等式(m+3)x>2m+6的解集为x<2,则m的取值范围为( )
A.m>0 B.m>﹣3 C.m<0 D.m<﹣3
9.如图,已知长方形纸片ABCD,点E、F在BC边上,点G、H在AD边上,分别沿EG、FH折叠,使点B和点C都落在点M处,若α+β=224°,则∠EMF的度数为( )
A.90° B.91° C.92° D.94°
10.如图,两个正方形的边长分别为a和b,如果a﹣b=2,ab=26,那么阴影部分的面积是( )
A.30 B.34 C.40 D.44
二、填空题:(本大题共4小题,每小题5分,共20分)
11.分解因式:3a2﹣6ab+3b2= .
12.已知某种流感病毒的形状如球形,直径大约为0.000000109m,将0.000000109m用科学记数法表示为 m.
13.已知9a=8,3b=4,则32a﹣b= .
14.已知直线AB∥CD,点E是AB上一点,点O、F是CD上不同的两点,且∠AEO=38°,作OM⊥OE,ON⊥OF,则∠MON的度数是 .
三、解答题(本大题共9小题,共90分)
15.计算:﹣22+(2021﹣π)0﹣+(﹣2)﹣1.
16.解不等式组:,并把其解集表示在数轴上.
17.先化简,再求值:(2x+1﹣)÷,其中x=3.
18.在正方形网格中,每个小正方形的边长均为1个单位长度,△ABC的三个顶点的位置如图所示,现将△ABC平移,使点C与点F重合,点D、E分别是A、B的对应点.
(1)请画出平移后的△DEF;
(2)若连接AD、BE,则这两条线段之间的关系是 ;
(3)△DEF的面积是 .
19.如图,点D、E、F分别为△ABC的边BC、CA、AB上的点,DE∥AB,∠A=∠EDF,∠C=60°,求∠BDF的度数.
20.根据疫情防控工作需要,某社区组织甲、乙两支医疗队开展疫苗接种工作,甲队比乙队每小时多接种30人,甲队接种2250人与乙队接种1800人用时相同.问甲队每小时接种多少人?
21.我们规定:当a≥b时,a☆b=a﹣b;当a<b时,a☆b=a2﹣b2.
(1)求5☆3的值;
(2)若m>0,化简:(m+3)☆(2m+3);
(3)若x☆3=7,求x的值.
22.已知:AB∥CD,点E在直线AB上,点F在直线CD上.
(1)如图①,EM平分∠BEF,FN平分∠CFE,试判断EM与FN的位置关系,并说明理由;
(2)如图②,EG平分∠MEF,EH平分∠AEM,试判断∠GEH与∠EFD的数量关系,并说明理由.
23.随着中国“十四五”规划的推进和国家政策的刺激,新能源板块成为重点发展的领域之一.某品牌汽车生产厂家生产了一批油电混合动力汽车和纯电动汽车,每辆油电混合动力汽车比纯电动汽车生产成本多1万元,现生产2000辆油电混合动力汽车与1600辆纯电动汽车共耗资21800万元.两款汽车的部分对比参数如表:
汽车类型 生产成本(万元/辆) 预售价(万元/辆) 补贴(万元/辆)
油电混合动力汽车
8.8 1.2
纯电动汽车
6.6 1.5
(1)每辆油电混合动力汽车的生产成本是多少万元?
(2)为扶持新能源汽车发展,消费者可享受新能源汽车的政府补贴.某上市公司准备用120万资金采购该品牌的新能源汽车共20辆,且油电混合动力汽车不少于5辆,该公司有几种购买方案?请为公司选择一种满足要求的最省钱的方案.
参考答案
一、选择题(本大题共10小题,每小题4分,共40分)
1.16的算术平方根是( )
A.﹣4 B.4 C. D.
解:由42=16,得
=4,故B符合题意,
故选:B.
2.下列运算正确的是( )
A.a+2a=3a2 B.(a2)3=a5 C.a3?a4=a12 D.(﹣3a)2=9a2
解:A.a+2a=3a,故此选项不符合题意;
B.(a2)3=a6,故此选项不符合题意;
C.a3?a4=a7,故此选项不符合题意;
D.(﹣3a)2=9a2,正确,故此选项符合题意,
故选:D.
3.如果分式的值为0,那么x的值是( )
A.x=3 B.x=±3 C.x≠3 D.x=﹣3
解:由题意得:x﹣3=0且x+3≠0,
解得:x=3,
故选:A.
4.如图,圆的直径为1个单位长度,该圆上的点A与数轴上表示1的点重合,将该圆沿数轴向左滚动1周,点A到达A′的位置,则点A′表示的数是( )
A.π﹣1 B.﹣π+1 C.﹣π﹣1 D.π﹣1或﹣π﹣1
解:∵圆的直径为1个单位长度,
∴此圆的周长=π,
∴当圆向左滚动时点A′表示的数是﹣π+1;
故选:B.
5.下列从左到右变形正确的是( )
A.= B.=
C.(a﹣b)2=a2﹣b2 D.(a﹣2)(a+3)=a2+a﹣6
解:A、≠,原变形错误,故此选项不符合题意.
B、当m=0时,此时无意义,原变形错误,故此选项不符合题意.
C、(a﹣b)2=a2﹣2ab+b2,原变形错误,故此选项不符合题意.
D、(a﹣2)(a+3)=a2+a﹣6,原变形正确,故此选项符合题意.
故选:D.
6.若两个连续整数x,y满足x<<y,则x+y的值是( )
A.5 B.6 C.7 D.8
解:∵9<10<16,
∴,
∴3<<4,
∴x=3,y=4,
∴x+y的值是3+4=7,
故选:C.
7.如果m2+m=5,那么代数式m(m﹣2)+(m+2)2的值为( )
A.14 B.9 C.﹣1 D.﹣6
解:m(m﹣2)+(m+2)2
=m2﹣2m+m2+4m+4
=2m2+2m+4.
当m2+m=5时,原式=2(m2+m)+4=2×5+4=10+4=14.
故选:A.
8.若不等式(m+3)x>2m+6的解集为x<2,则m的取值范围为( )
A.m>0 B.m>﹣3 C.m<0 D.m<﹣3
解:∵(m+3)x>2m+6的解集为x<2,
∴m+3<0,
解得m<﹣3,
故选:D.
9.如图,已知长方形纸片ABCD,点E、F在BC边上,点G、H在AD边上,分别沿EG、FH折叠,使点B和点C都落在点M处,若α+β=224°,则∠EMF的度数为( )
A.90° B.91° C.92° D.94°
解:∵四边形ABCD是长方形,
∴AD∥BC,
∴∠BEG+α=180°,∠CFH+β=180°,
∴∠BEG=180°﹣α,∠CFH=180°﹣β,
∵α+β=224°,
∴∠BEG+∠CFH=360°﹣(α+β)=136°,
由折叠可知:
∠BEG=∠GEM,∠CFH=∠HFM,
∴∠BEM+∠CFM=2(∠BEG+∠CFH)=272°,
∴∠MEF+∠MFE=360°﹣(∠BEM+∠CFM)=360°﹣272°=88°,
∴∠EMF=180°﹣(∠MEF+∠MFE)=92°,
故选:C.
10.如图,两个正方形的边长分别为a和b,如果a﹣b=2,ab=26,那么阴影部分的面积是( )
A.30 B.34 C.40 D.44
解:如图,
∵a﹣b=2,ab=26,
∴a2﹣2ab+b2=4,
∴a2+b2=4+2ab=4+52=56,
阴影部分的面积=S△ABC+S△CDM+S△AEF+S△GHM
=2×(a﹣b)×a+2×b×b
=a(a﹣b)+b2
=a2+b2﹣ab
=56﹣26
=30.
故选:A.
二、填空题:(本大题共4小题,每小题5分,共20分)
11.分解因式:3a2﹣6ab+3b2= 3(a﹣b)2 .
解:3a2﹣6ab+3b2
=3(a2﹣2ab+b2)
=3(a﹣b)2.
故答案为:3(a﹣b)2.
12.已知某种流感病毒的形状如球形,直径大约为0.000000109m,将0.000000109m用科学记数法表示为 1.09×10﹣7 m.
解:将0.000000109m用科学记数法表示为1.09×10﹣7m.
故答案是:1.09×10﹣7.
13.已知9a=8,3b=4,则32a﹣b= 2 .
解:原式=32a÷3b=(32)a÷3b=9a÷3b=8÷4=2,
故答案为:2.
14.已知直线AB∥CD,点E是AB上一点,点O、F是CD上不同的两点,且∠AEO=38°,作OM⊥OE,ON⊥OF,则∠MON的度数是 38°或者142° .
解:根据题意有图1、图2两种情况:
图1中,
∵AB∥CD,
∴∠AEO=∠DO=38°,
∵MO⊥OE,ON⊥OF,
∴∠MOE=∠NOF=90°,
∴∠MON=90°﹣(90°﹣38°)=38°;
图2中,
∵AB∥CD,
∴∠AEO=∠DOE=38°,
∵MO⊥OE,ON⊥OF,
∴∠MOE=∠NOF=90°,
∴∠MON=180°﹣38°=142°
综上,∠MON的度数为38°或者142°.
故答案为:38°或者142°.
三、解答题(本大题共9小题,共90分)
15.计算:﹣22+(2021﹣π)0﹣+(﹣2)﹣1.
【解答】原式=﹣4+1﹣(﹣2)+(﹣)
=﹣4+1+2﹣
=﹣.
16.解不等式组:,并把其解集表示在数轴上.
解:,
由①得,x>3,
由②得,x≤5,
故此不等式组的解集为:3<x≤5.
在数轴上表示为:
.
17.先化简,再求值:(2x+1﹣)÷,其中x=3.
解:原式=[﹣]÷
=?
=
=
=4x+8,
当x=3时,
原式=4×3+8
=20.
18.在正方形网格中,每个小正方形的边长均为1个单位长度,△ABC的三个顶点的位置如图所示,现将△ABC平移,使点C与点F重合,点D、E分别是A、B的对应点.
(1)请画出平移后的△DEF;
(2)若连接AD、BE,则这两条线段之间的关系是 AD∥BE,AD=BE ;
(3)△DEF的面积是 .
解:(1)如图,△DEF即为所求.
(2)观察图形可知AD∥BE,AD=BE.
故答案为:AD∥BE,AD=BE.
(3)S△DEF=×5×3=,
故答案为:.
19.如图,点D、E、F分别为△ABC的边BC、CA、AB上的点,DE∥AB,∠A=∠EDF,∠C=60°,求∠BDF的度数.
解:∵DE∥AB,
∴∠A=∠CED,
∵∠A=∠EDF,
∴∠EDF=∠CED,
∴DF∥AC,
∴∠BDF=∠C,
∵∠C=60°,
∴∠BDF=60°.
20.根据疫情防控工作需要,某社区组织甲、乙两支医疗队开展疫苗接种工作,甲队比乙队每小时多接种30人,甲队接种2250人与乙队接种1800人用时相同.问甲队每小时接种多少人?
解:设甲队每小时接种x人,则乙队每小时接种(x﹣30)人,
依题意得:=,
解得:x=150,
经检验,x=150是原方程的解,且符合题意.
答:甲队每小时接种150人.
21.我们规定:当a≥b时,a☆b=a﹣b;当a<b时,a☆b=a2﹣b2.
(1)求5☆3的值;
(2)若m>0,化简:(m+3)☆(2m+3);
(3)若x☆3=7,求x的值.
解:(1)∵5>3,
∴原式=5﹣3=2;
(2)当m>0时,
∵m+3﹣(2m+3)
=m+3﹣2m﹣3
=﹣m<0,
∴m+3<2m+3,
∴原式=(m+3)2﹣(2m+3)2
=(m+3+2m+3)[m+3﹣(2m+3)]
=(m+3+2m+3)(﹣m)
=(3m+6)(﹣m)
=﹣3m2﹣6m;
(3)当x≥3时,x﹣3=7,
解得:x=10;
当x<3时,x2﹣32=7,
解得:x=±4,
∵x<3,
∴x=4不符合题意,
∴x=﹣4;
综上所述,x=10或﹣4.
22.已知:AB∥CD,点E在直线AB上,点F在直线CD上.
(1)如图①,EM平分∠BEF,FN平分∠CFE,试判断EM与FN的位置关系,并说明理由;
(2)如图②,EG平分∠MEF,EH平分∠AEM,试判断∠GEH与∠EFD的数量关系,并说明理由.
解:(1)如图①位置关系是:EM∥FN,理由:
∵AB∥CD,
∴∠BEF=∠CFE,
∵EM平分∠BEF,FN平分∠CFE,
∴∠MEF=∠BEF,∠NFE=∠CFE,
∴∠MEF=∠NFE,
∴EM∥FN;
(2)如图②,∠EFD=2∠GEH,理由:
∵EG平分∠MEF,
∴∠MEG=∠GEH+∠HEF,
∵EH平分∠AEM,
∴∠MEG+∠GEH=∠AEF+∠HEF,
∴∠AEF=2∠GEH,
∵AB∥CD,
∴∠AEF=∠EFD,
∴∠EFD=2∠GEH.
23.随着中国“十四五”规划的推进和国家政策的刺激,新能源板块成为重点发展的领域之一.某品牌汽车生产厂家生产了一批油电混合动力汽车和纯电动汽车,每辆油电混合动力汽车比纯电动汽车生产成本多1万元,现生产2000辆油电混合动力汽车与1600辆纯电动汽车共耗资21800万元.两款汽车的部分对比参数如表:
汽车类型 生产成本(万元/辆) 预售价(万元/辆) 补贴(万元/辆)
油电混合动力汽车
8.8 1.2
纯电动汽车
6.6 1.5
(1)每辆油电混合动力汽车的生产成本是多少万元?
(2)为扶持新能源汽车发展,消费者可享受新能源汽车的政府补贴.某上市公司准备用120万资金采购该品牌的新能源汽车共20辆,且油电混合动力汽车不少于5辆,该公司有几种购买方案?请为公司选择一种满足要求的最省钱的方案.
解:(1)设每辆油电混合动力汽车的生产成本是x万元,则每辆纯电动汽车的生产成本是(x﹣1)万元,
依题意得:2000x+1600(x﹣1)=21800,
解得:x=6.5,
答:每辆油电混合动力汽车的生产成本是6.5万元.
(2)设购进油电混合动力汽车m辆,则购进纯电动汽车(20﹣m)辆,
依题意得:,
解得:5≤m≤,
又∵m为整数,
∴m可以取5,6,7,
∴该公司共有3种购买方案,
方案1:购进油电混合动力汽车5辆,纯电动汽车15辆,所需费用为(8.8﹣1.2)×5+(6.6﹣1.5)×15=114.5(万元);
方案2:购进油电混合动力汽车6辆,纯电动汽车14辆,所需费用为(8.8﹣1.2)×6+(6.6﹣1.5)×14=117(万元);
方案3:购进油电混合动力汽车7辆,纯电动汽车13辆,所需费用为(8.8﹣1.2)×7+(6.6﹣1.5)×13=119.5(万元).
∵114.5<117<119.5,
∴最省钱的方案为:购进油电混合动力汽车5辆,纯电动汽车15辆.
同课章节目录
