福建省漳州市芗城中学2011-2012学年高二下学期期中考试数学(理)试题
文档属性
| 名称 | 福建省漳州市芗城中学2011-2012学年高二下学期期中考试数学(理)试题 |  | |
| 格式 | zip | ||
| 文件大小 | 195.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-04-25 19:30:31 | ||
图片预览


文档简介
一、选择题(本大题共12道小题,每小题5分, 共60分,在每小题给出的四个选项中,只有一项是符合题目要求的.)
1.的导数是( )
A.0 B.1 C.不存在 D.不确定
2. 复数等于( )
A. B. C. D.
3.设a=(x,2y,3),b=(1,1,6),且a∥b,则x+y等于( )
A. B. C. D.2
4.若a=(0,1,-1),b=(1,1,0),且(a+λb)⊥a,则实数λ的值是( )
A.-1 B.0 C.1 D.-2
5.曲线在处的切线斜率为( )
A. B. C. D.
6.等于( )
A.1 B. C. D.
7. 复数=( )
A、1 B、i C、0 D、-1
8.若向量(1,0,z)与向量(2,1,0)的夹角的余弦值为,则z等于( )
A.0 B.1 C.-1 D.2
9.在复平面内,复数对应的点位于( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
10.若直线l的方向向量为a=(1,-1,2),平面α的法向量为u=(-2,2,-4),则( )
A.l∥α B.l⊥α C.l α D.l与α斜交
11. 已知复数满足,则复数在复平面上对应点所表示的图形是( )
A 圆 B 椭圆 C 双曲线 D 直线
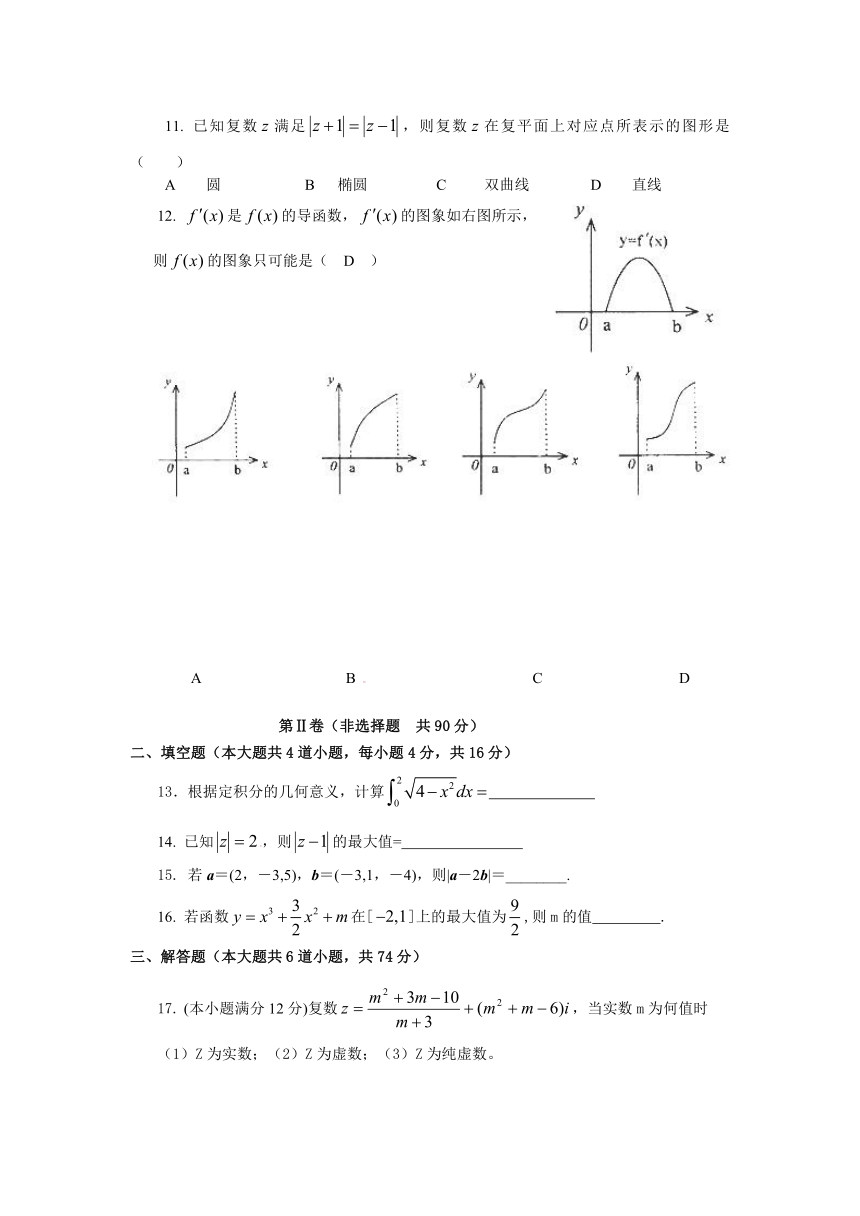
12. 是的导函数,的图象如右图所示,
则的图象只可能是( D )
A B C D
第Ⅱ卷(非选择题 共90分)
二、填空题(本大题共4道小题,每小题4分,共16分)
13.根据定积分的几何意义,计算
14. 已知,则的最大值=
15. 若a=(2,-3,5),b=(-3,1,-4),则|a-2b|=________.
16. 若函数在[]上的最大值为,则m的值 .
三、解答题(本大题共6道小题,共74分)
17. (本小题满分12分)复数,当实数m为何值时
(1)Z为实数;(2)Z为虚数;(3)Z为纯虚数。
18. (本小题满分12分)已知x、y为共轭复数,且,求x、y.
19.(本小题满分12分)如图,在直三棱柱ABC-A1B1C1中,∠BAC=90°,AB=AC=AA1=1.D是棱CC1上的中点,P是AD的延长线与A1C1的延长线的交点.
(1)求二面角A-A1D-B的平面角的余弦值;
(2)求点C到平面B1DP的距离.
20.(本小题满分12分)某商场从生产厂家以每件20元购进一批商品,若该商品零售价定为p元,则销量Q(单位:件)与零售价p(单位:元)有如下关系:.问该商品售价定为多少元时毛利润L最大,并求最大毛利润(毛利润=销售收入-进货支出)。
21. (本小题满分12分) 已知函数在处取得极值,过点作曲线的切线,(1)求此切线的方程.(2)求切线与函数的图象围成的平面图形的面积。
22. (本小题满分14分)设函数.
(1)求函数的单调区间和极值;
(2)若关于x的方程有三个不同实根,求实数的取值范围;
(3)已知当恒成立,求实数k的取值范围。
芗城中学11-12学年下学期高二年数学(理科)期中考答案
一、选择题(本大题共12道小题,每小题5分, 共60分)
1 2 3 4 5 6 7 8 9 10 11 12
A D B D C C A A D B D D
二、填空题(本大题共4道小题,每小题4分,共16分)
13. 14. 3 15. 16. 2
三、解答题(本大题共6道小题,共74分)
18.解:设,则, ,,
因此有,
即且,所以且,
所以或
19
解析: 如图,以A1为原点,A1B1,A1C1,A1A所在直线分别为x轴,y轴,z轴建立空间直角坐标系,则A1(0,0,0),B1(1,0,0),C1(0,1,0),B(1,0,1).D(0,1, )
设平面BA1D的一个法向量为n1=(x,y,z),
解得
取,得n1=(2,-1,2).
又n2=(1,0,0)为平面AA1D的一个法向量,
∴cos〈n1·n2〉===.
故二面角A-A1D-B的平面角的余弦值为.
(3)∵=(1,-2,0),=,
设平面B1DP的一个法向量为n3=(a1,b1,c1).
令c1=1,可得n3=.
又=,
∴C到平面B1DP的距离d==.
21解:(1),依题意,
,即 解得
∴,
曲线方程为,点不在曲线上。
设切点为,则
由知,切线方程为
又点在切线上,有
化简得 ,解得
所以切点为,切线方程为y=2
(2)
与y=2的交点为(1,2)和(2,2)
切线与函数g(x)的图象围成的图形面积为:
1.的导数是( )
A.0 B.1 C.不存在 D.不确定
2. 复数等于( )
A. B. C. D.
3.设a=(x,2y,3),b=(1,1,6),且a∥b,则x+y等于( )
A. B. C. D.2
4.若a=(0,1,-1),b=(1,1,0),且(a+λb)⊥a,则实数λ的值是( )
A.-1 B.0 C.1 D.-2
5.曲线在处的切线斜率为( )
A. B. C. D.
6.等于( )
A.1 B. C. D.
7. 复数=( )
A、1 B、i C、0 D、-1
8.若向量(1,0,z)与向量(2,1,0)的夹角的余弦值为,则z等于( )
A.0 B.1 C.-1 D.2
9.在复平面内,复数对应的点位于( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
10.若直线l的方向向量为a=(1,-1,2),平面α的法向量为u=(-2,2,-4),则( )
A.l∥α B.l⊥α C.l α D.l与α斜交
11. 已知复数满足,则复数在复平面上对应点所表示的图形是( )
A 圆 B 椭圆 C 双曲线 D 直线
12. 是的导函数,的图象如右图所示,
则的图象只可能是( D )
A B C D
第Ⅱ卷(非选择题 共90分)
二、填空题(本大题共4道小题,每小题4分,共16分)
13.根据定积分的几何意义,计算
14. 已知,则的最大值=
15. 若a=(2,-3,5),b=(-3,1,-4),则|a-2b|=________.
16. 若函数在[]上的最大值为,则m的值 .
三、解答题(本大题共6道小题,共74分)
17. (本小题满分12分)复数,当实数m为何值时
(1)Z为实数;(2)Z为虚数;(3)Z为纯虚数。
18. (本小题满分12分)已知x、y为共轭复数,且,求x、y.
19.(本小题满分12分)如图,在直三棱柱ABC-A1B1C1中,∠BAC=90°,AB=AC=AA1=1.D是棱CC1上的中点,P是AD的延长线与A1C1的延长线的交点.
(1)求二面角A-A1D-B的平面角的余弦值;
(2)求点C到平面B1DP的距离.
20.(本小题满分12分)某商场从生产厂家以每件20元购进一批商品,若该商品零售价定为p元,则销量Q(单位:件)与零售价p(单位:元)有如下关系:.问该商品售价定为多少元时毛利润L最大,并求最大毛利润(毛利润=销售收入-进货支出)。
21. (本小题满分12分) 已知函数在处取得极值,过点作曲线的切线,(1)求此切线的方程.(2)求切线与函数的图象围成的平面图形的面积。
22. (本小题满分14分)设函数.
(1)求函数的单调区间和极值;
(2)若关于x的方程有三个不同实根,求实数的取值范围;
(3)已知当恒成立,求实数k的取值范围。
芗城中学11-12学年下学期高二年数学(理科)期中考答案
一、选择题(本大题共12道小题,每小题5分, 共60分)
1 2 3 4 5 6 7 8 9 10 11 12
A D B D C C A A D B D D
二、填空题(本大题共4道小题,每小题4分,共16分)
13. 14. 3 15. 16. 2
三、解答题(本大题共6道小题,共74分)
18.解:设,则, ,,
因此有,
即且,所以且,
所以或
19
解析: 如图,以A1为原点,A1B1,A1C1,A1A所在直线分别为x轴,y轴,z轴建立空间直角坐标系,则A1(0,0,0),B1(1,0,0),C1(0,1,0),B(1,0,1).D(0,1, )
设平面BA1D的一个法向量为n1=(x,y,z),
解得
取,得n1=(2,-1,2).
又n2=(1,0,0)为平面AA1D的一个法向量,
∴cos〈n1·n2〉===.
故二面角A-A1D-B的平面角的余弦值为.
(3)∵=(1,-2,0),=,
设平面B1DP的一个法向量为n3=(a1,b1,c1).
令c1=1,可得n3=.
又=,
∴C到平面B1DP的距离d==.
21解:(1),依题意,
,即 解得
∴,
曲线方程为,点不在曲线上。
设切点为,则
由知,切线方程为
又点在切线上,有
化简得 ,解得
所以切点为,切线方程为y=2
(2)
与y=2的交点为(1,2)和(2,2)
切线与函数g(x)的图象围成的图形面积为:
同课章节目录
