华师大版13.5.3角平分线的性质(30张PPT)
文档属性
| 名称 | 华师大版13.5.3角平分线的性质(30张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-07 18:48:33 | ||
图片预览









文档简介
(共30张PPT)
在练习本上画一个角,怎样得到这个角的平分线?
问题2:在生产生活中,这些方法是否可行呢?
用量角器度量,也可用折纸的方法.
导入
明德双语学校
张华平
华师大版八年级数学上册
13.5.3角平分线的性质
第1课时
1.会用尺规作一个角的平分线,知道作法的合理性.
2.探索并证明角的平分线的性质.
3.能用角的平分线的性质解决简单问题.
探索并证明角的平分线的性质.
学习目标:
学习重点:
自主探究
请大家认真翻阅课本96页,完成下面题目。
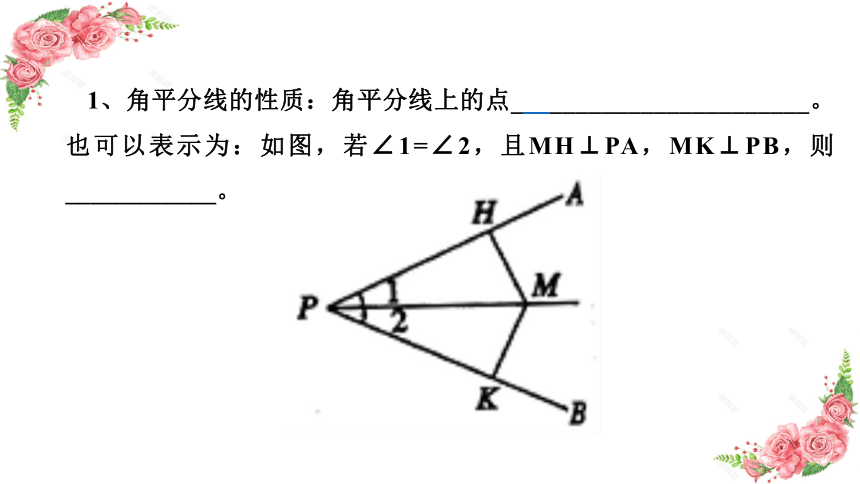
1、角平分线的性质:角平分线上的点_______________________。也可以表示为:如图,若∠1=∠2,且MH⊥PA,MK⊥PB,则____________。
?
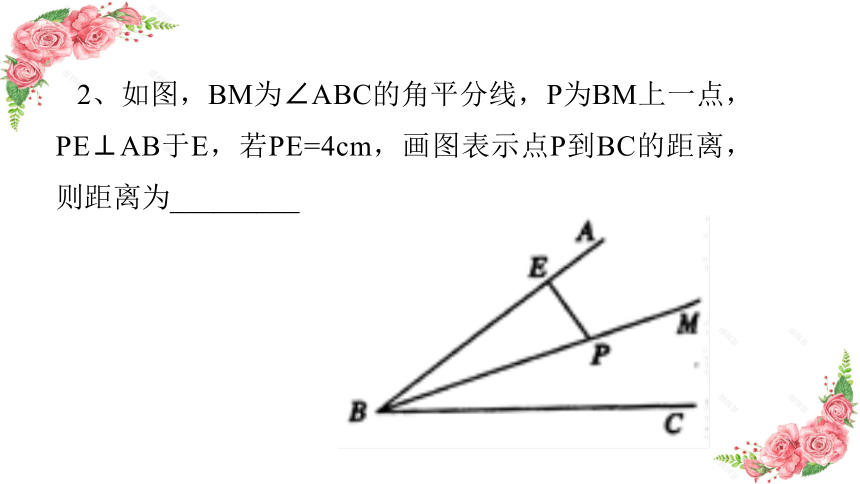
2、如图,BM为∠ABC的角平分线,P为BM上一点,PE⊥AB于E,若PE=4cm,画图表示点P到BC的距离,则距离为_________
3、如图,AB∥CD,用直尺和圆规作∠C的平分线CP,CP交AB于点E。(保留作图痕迹,不写作法)
4、如图,∠A=∠C=90°,根据角平分线的性质填空:
1)若∠1=∠2,则_______=__________;
2)若∠3=∠4,则_______=__________.
合作探究
请将各自的学习成果在组内展示,组长记录意见不一致的地方,组内就意见不一致的地方展开讨论,统一意见。确定一名代表作为展示代表,再选出一名代表作为评价代表。
下图是一个平分角的仪器,其中AB
=AD,
BC
=DC,将点A
放在角的顶点,AB
和AD
沿着角的两
边放下,沿AC
画一条射线AE,AE
就是∠DAB
的平分
线.你能说明它的道理吗?
A
B
D
C
E
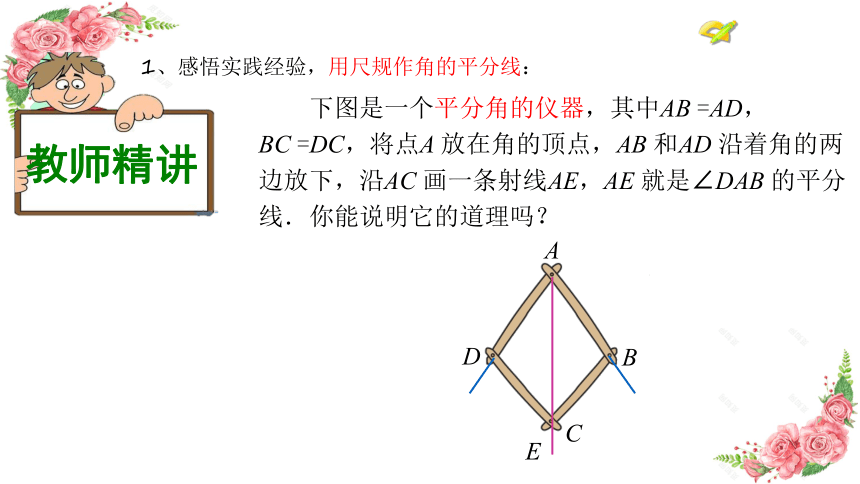
教师精讲
1、感悟实践经验,用尺规作角的平分线:
B
D
A
C
E
【解析】
在△ACD和△ACB中
AD=AB(已知)
DC=BC(已知)
CA=CA(公共边)
所以△ACD≌
△ACB(SSS)
所以∠CAD=∠CAB(全等三角形的对应角相等)
所以AC平分∠DAB(角平分线的定义)
从利用平分角的仪器画角的平分线中,你受到哪些启发?如何利用直尺和圆规作一个角的平分线?
利用尺规作角的平分线的具体方法:
A
B
O
M
N
C
1.以O为圆心,适当长为半径作弧,交OA于M,交OB于N.
2.分别以M,N为圆心.大于
1/2
MN的长为半径作弧.两弧在∠AOB的内部交于C.
3.作射线OC.
射线OC即为所求.
你能说明为什么射线OC
是∠AOB
的平分线吗?
A
B
O
M
N
C
已知:OM=ON,MC=NC。
求证:OC平分∠AOB。
证明:在△OMC和△ONC中,
OM=ON,
MC=NC,
OC=OC,
∴
△OMC≌
△ONC(SSS)
∴∠MOC=∠NOC
即:OC平分∠AOB
2.角平分线有什么性质呢?
OC是∠AOB的平分线,点P是射线OC上的任意一点,
1.
操作测量:取点P的三个不同的位置,分别过点P作PD⊥OA,PE
⊥OB,点D、E为垂足,测量PD、PE的长.将三次数据填入下表:
2.
观察测量结果,猜想线段PD与PE的大小关系,
写出结论:____________
PD
PE
第一次
第二次
第三次
C
O
B
A
PD=PE
p
D
E
教师精讲
已知:∠AOC
=
∠BOC,点
P在OC上,PD⊥OA,PE⊥OB,
垂足分别为D,E.
求证:PD
=PE.
通过动手实验、观察比较,我们发现“角的平分线上的点到角的两边的距离相等”,你能通过严格的逻辑推理证明这个结论吗?
A
B
O
P
C
D
E
证明:∵
PD⊥OA,PE⊥OB(已知)
∴∠PDO=∠PEO=90(垂直的定义)
在△PDO和△PEO中
∴
PD=PE(全等三角形的对应边相等)
∠
PDO=
∠
PEO
∠
AOC=
∠
BOC
OP=OP
∴
△
PDO≌
△
PEO(AAS)
D
P
E
A
O
B
C
P到OA的距离
P到OB的距离
角平分线上的点
几何语言:
∵
OC平分∠AOB,
且PD⊥OA,
PE⊥OB
∴
PD=
PE
角的平分线上的点到角的两边的距离相等。
角平分线的性质:
O
D
E
P
A
C
B
角平分线的性质
角的平分线上的点到角的两边的距离相等。
B
A
D
O
P
E
C
定理应用所具备的条件:
(1)角的平分线;
(2)点在该平分线上;
(3)垂直距离。
定理的作用:
证明线段相等。
∵
如图,AD平分∠BAC(已知)
∴
=
,(
)
在角的平分线上的点到这个角的两边的距离相等。
BD
CD
(×)
练习一
小练笔:
∵
如图,
DC⊥AC,DB⊥AB
(已知)
∴
=
,(
)
在角的平分线上的点到这个角的两边的距离相等。
BD
CD
(×)
∵
AD平分∠BAC,
DC⊥AC,DB⊥AB
(已知)
∴
=
,(
)
DB
DC
在角的平分线上的点到这个角的两边的距离相等。
√
不必再证全等
如图,
∵
OC是∠AOB的平分线,
又
________________
∴PD=PE
(
)
PD⊥OA,PE⊥OB
B
O
A
C
D
P
E
角的平分线上的点
到角的两边的距离相等
解
作∠AOB的角平分线,交EF于一点,则这点即为所
求作的点P.(提示:用尺规作图)
2.如图,在直线EF上求作一点P
,使点P到∠AOB两边
的距离相等.
P
练习二
3、如图,BD是∠ABC的平分线,DE⊥AB于E,S△ABC=30cm2,AB=18cm,BC=12cm,则DE=________.
练习三
◆这节课我们学习了哪些知识?
1、“作已知角的平分线”的尺规作图法;
2、角的平分线的性质:
∵
OC是∠AOB的平分线,
又
PD⊥OA,PE⊥OB
∴
PD=PE
(角的平分线上的点
到角的两边距离相等).
E
D
O
A
B
P
C
几何语言:
角的平分线上的点到角的两边的距离相等。
小结:
反过来,到一个角的两边的距离相等
的点是否一定在这个角的平分线上呢?
P
已知:如图,PD⊥OA,PE⊥OB,
点D、E为垂足,PD=PE.
求证:点P在∠AOB的平分线上
拓展:
P
C
证明:
经过点P作射线OC
∵
PD⊥OA,PE⊥OB
∴
∠PDO=∠PEO=90°
在Rt△PDO和Rt△PEO中
PO=PO
PD=PE
∴
Rt△PDO≌Rt△PEO(HL)
∴
∠
POD=∠POE
∴点P在∠AOB的平分线上
已知:如图,PD⊥OA,PE⊥OB,
点D、E为垂足,PD=PE.
求证:点P在∠AOB的平分线上.
1、如图,在△ABC中,∠B、∠C的平分线交于O,
OD⊥AB于D,OE⊥AC于E,
则OD与OE的大小关系是(
)
A、OD
>
OE
B、OD=OE
C、OD
<
OE
D、不能确定
作业:
作业:
2.如图,BD平分∠ABC,∠DAB+∠DCB=180°,
求证:AD=CD.
That`s
all!
Thank
you!
在练习本上画一个角,怎样得到这个角的平分线?
问题2:在生产生活中,这些方法是否可行呢?
用量角器度量,也可用折纸的方法.
导入
明德双语学校
张华平
华师大版八年级数学上册
13.5.3角平分线的性质
第1课时
1.会用尺规作一个角的平分线,知道作法的合理性.
2.探索并证明角的平分线的性质.
3.能用角的平分线的性质解决简单问题.
探索并证明角的平分线的性质.
学习目标:
学习重点:
自主探究
请大家认真翻阅课本96页,完成下面题目。
1、角平分线的性质:角平分线上的点_______________________。也可以表示为:如图,若∠1=∠2,且MH⊥PA,MK⊥PB,则____________。
?
2、如图,BM为∠ABC的角平分线,P为BM上一点,PE⊥AB于E,若PE=4cm,画图表示点P到BC的距离,则距离为_________
3、如图,AB∥CD,用直尺和圆规作∠C的平分线CP,CP交AB于点E。(保留作图痕迹,不写作法)
4、如图,∠A=∠C=90°,根据角平分线的性质填空:
1)若∠1=∠2,则_______=__________;
2)若∠3=∠4,则_______=__________.
合作探究
请将各自的学习成果在组内展示,组长记录意见不一致的地方,组内就意见不一致的地方展开讨论,统一意见。确定一名代表作为展示代表,再选出一名代表作为评价代表。
下图是一个平分角的仪器,其中AB
=AD,
BC
=DC,将点A
放在角的顶点,AB
和AD
沿着角的两
边放下,沿AC
画一条射线AE,AE
就是∠DAB
的平分
线.你能说明它的道理吗?
A
B
D
C
E
教师精讲
1、感悟实践经验,用尺规作角的平分线:
B
D
A
C
E
【解析】
在△ACD和△ACB中
AD=AB(已知)
DC=BC(已知)
CA=CA(公共边)
所以△ACD≌
△ACB(SSS)
所以∠CAD=∠CAB(全等三角形的对应角相等)
所以AC平分∠DAB(角平分线的定义)
从利用平分角的仪器画角的平分线中,你受到哪些启发?如何利用直尺和圆规作一个角的平分线?
利用尺规作角的平分线的具体方法:
A
B
O
M
N
C
1.以O为圆心,适当长为半径作弧,交OA于M,交OB于N.
2.分别以M,N为圆心.大于
1/2
MN的长为半径作弧.两弧在∠AOB的内部交于C.
3.作射线OC.
射线OC即为所求.
你能说明为什么射线OC
是∠AOB
的平分线吗?
A
B
O
M
N
C
已知:OM=ON,MC=NC。
求证:OC平分∠AOB。
证明:在△OMC和△ONC中,
OM=ON,
MC=NC,
OC=OC,
∴
△OMC≌
△ONC(SSS)
∴∠MOC=∠NOC
即:OC平分∠AOB
2.角平分线有什么性质呢?
OC是∠AOB的平分线,点P是射线OC上的任意一点,
1.
操作测量:取点P的三个不同的位置,分别过点P作PD⊥OA,PE
⊥OB,点D、E为垂足,测量PD、PE的长.将三次数据填入下表:
2.
观察测量结果,猜想线段PD与PE的大小关系,
写出结论:____________
PD
PE
第一次
第二次
第三次
C
O
B
A
PD=PE
p
D
E
教师精讲
已知:∠AOC
=
∠BOC,点
P在OC上,PD⊥OA,PE⊥OB,
垂足分别为D,E.
求证:PD
=PE.
通过动手实验、观察比较,我们发现“角的平分线上的点到角的两边的距离相等”,你能通过严格的逻辑推理证明这个结论吗?
A
B
O
P
C
D
E
证明:∵
PD⊥OA,PE⊥OB(已知)
∴∠PDO=∠PEO=90(垂直的定义)
在△PDO和△PEO中
∴
PD=PE(全等三角形的对应边相等)
∠
PDO=
∠
PEO
∠
AOC=
∠
BOC
OP=OP
∴
△
PDO≌
△
PEO(AAS)
D
P
E
A
O
B
C
P到OA的距离
P到OB的距离
角平分线上的点
几何语言:
∵
OC平分∠AOB,
且PD⊥OA,
PE⊥OB
∴
PD=
PE
角的平分线上的点到角的两边的距离相等。
角平分线的性质:
O
D
E
P
A
C
B
角平分线的性质
角的平分线上的点到角的两边的距离相等。
B
A
D
O
P
E
C
定理应用所具备的条件:
(1)角的平分线;
(2)点在该平分线上;
(3)垂直距离。
定理的作用:
证明线段相等。
∵
如图,AD平分∠BAC(已知)
∴
=
,(
)
在角的平分线上的点到这个角的两边的距离相等。
BD
CD
(×)
练习一
小练笔:
∵
如图,
DC⊥AC,DB⊥AB
(已知)
∴
=
,(
)
在角的平分线上的点到这个角的两边的距离相等。
BD
CD
(×)
∵
AD平分∠BAC,
DC⊥AC,DB⊥AB
(已知)
∴
=
,(
)
DB
DC
在角的平分线上的点到这个角的两边的距离相等。
√
不必再证全等
如图,
∵
OC是∠AOB的平分线,
又
________________
∴PD=PE
(
)
PD⊥OA,PE⊥OB
B
O
A
C
D
P
E
角的平分线上的点
到角的两边的距离相等
解
作∠AOB的角平分线,交EF于一点,则这点即为所
求作的点P.(提示:用尺规作图)
2.如图,在直线EF上求作一点P
,使点P到∠AOB两边
的距离相等.
P
练习二
3、如图,BD是∠ABC的平分线,DE⊥AB于E,S△ABC=30cm2,AB=18cm,BC=12cm,则DE=________.
练习三
◆这节课我们学习了哪些知识?
1、“作已知角的平分线”的尺规作图法;
2、角的平分线的性质:
∵
OC是∠AOB的平分线,
又
PD⊥OA,PE⊥OB
∴
PD=PE
(角的平分线上的点
到角的两边距离相等).
E
D
O
A
B
P
C
几何语言:
角的平分线上的点到角的两边的距离相等。
小结:
反过来,到一个角的两边的距离相等
的点是否一定在这个角的平分线上呢?
P
已知:如图,PD⊥OA,PE⊥OB,
点D、E为垂足,PD=PE.
求证:点P在∠AOB的平分线上
拓展:
P
C
证明:
经过点P作射线OC
∵
PD⊥OA,PE⊥OB
∴
∠PDO=∠PEO=90°
在Rt△PDO和Rt△PEO中
PO=PO
PD=PE
∴
Rt△PDO≌Rt△PEO(HL)
∴
∠
POD=∠POE
∴点P在∠AOB的平分线上
已知:如图,PD⊥OA,PE⊥OB,
点D、E为垂足,PD=PE.
求证:点P在∠AOB的平分线上.
1、如图,在△ABC中,∠B、∠C的平分线交于O,
OD⊥AB于D,OE⊥AC于E,
则OD与OE的大小关系是(
)
A、OD
>
OE
B、OD=OE
C、OD
<
OE
D、不能确定
作业:
作业:
2.如图,BD平分∠ABC,∠DAB+∠DCB=180°,
求证:AD=CD.
That`s
all!
Thank
you!
