《1.2矩形的性质与判定》同步能力达标训练(附解析)2021-2022学年九年级数学北师大版上册
文档属性
| 名称 | 《1.2矩形的性质与判定》同步能力达标训练(附解析)2021-2022学年九年级数学北师大版上册 |

|
|
| 格式 | doc | ||
| 文件大小 | 285.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-07 00:00:00 | ||
图片预览


文档简介
2021年北师大版九年级数学上册《1.2矩形的性质与判定》同步能力达标训练(附答案)
1.如图,四边形ABCD的对角线互相平分,若∠ABC=90°,则四边形ABCD为( )
A.菱形 B.矩形 C.菱形或矩形 D.无法判断
2.如图平行四边形ABCD中,AC、BD相交于点O,下列结论:①OA=OC,②∠BAD=∠BCD,③∠BAD+∠ABC=180°,④AC⊥BD,⑤AB=CD,正确结论的个数是( )
A.5个 B.4个 C.3个 D.2个
3.如图,在△ABC中,∠BAC=90°,AB=3,AC=4,P为边BC上一动点,PE⊥AB于E,PF⊥AC于F,则EF的最小值为( )
A.1.2 B.1.25 C.2.4 D.2.5
4.如图,点O是菱形ABCD对角线的交点,DE∥AC,CE∥BD,连接OE,设AC=12,BD=16,则OE的长为( )
A.8 B.9 C.10 D.12
5.矩形ABCD与ECFG如图放置,点B,C,F共线,点C,E,D共线,连接AG,取AG的中点H,连接EH.若AB=CF=4,BC=CE=2,则EH=( )
A. B.2 C. D.
6.已知:如图,矩形ABCD中,AB=5,BC=12,对角线AC、BD相交于点O,点P是线段AD上任意一点,且PE⊥BD于点E,PF⊥AC于点F,则PE+PF等于( )
A. B. C. D.
7.如图,在矩形OABC中,点B的坐标是(1,3),则AC的长是( )
A.3 B.2 C. D.4
8.如图,矩形ABCD由3×4个小正方形组成,此图中不是正方形的矩形有( )
A.34个 B.36个 C.38个 D.40个
9.如图,在长方形ABCD中,AB=10,BC=3,点E是AB的中点,点P在边DC上运动,若△APE是腰长为5的等腰三角形,则DP的长为 .
10.如图,矩形ABCD中,BC=8,AB=6,点E为CD边上一动点(不与C,D重合).以CE为边向外作矩形CEFG,且CE:CG=3:4,连接BF,点O是线段BF的中点.连接OE,则OE的最小值为 .
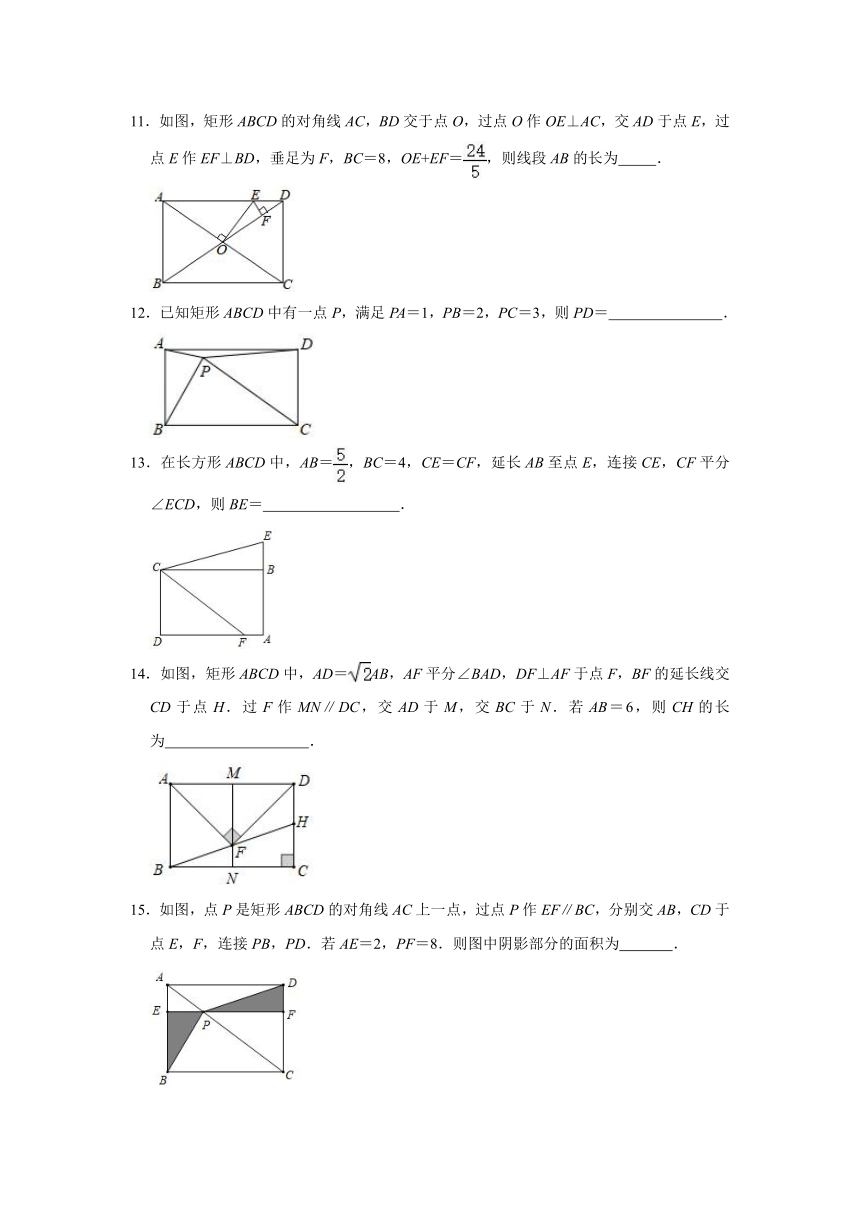
11.如图,矩形ABCD的对角线AC,BD交于点O,过点O作OE⊥AC,交AD于点E,过点E作EF⊥BD,垂足为F,BC=8,OE+EF=,则线段AB的长为 .
12.已知矩形ABCD中有一点P,满足PA=1,PB=2,PC=3,则PD= .
13.在长方形ABCD中,AB=,BC=4,CE=CF,延长AB至点E,连接CE,CF平分∠ECD,则BE= .
14.如图,矩形ABCD中,AD=AB,AF平分∠BAD,DF⊥AF于点F,BF的延长线交CD于点H.过F作MN∥DC,交AD于M,交BC于N.若AB=6,则CH的长为 .
15.如图,点P是矩形ABCD的对角线AC上一点,过点P作EF∥BC,分别交AB,CD于点E,F,连接PB,PD.若AE=2,PF=8.则图中阴影部分的面积为 .
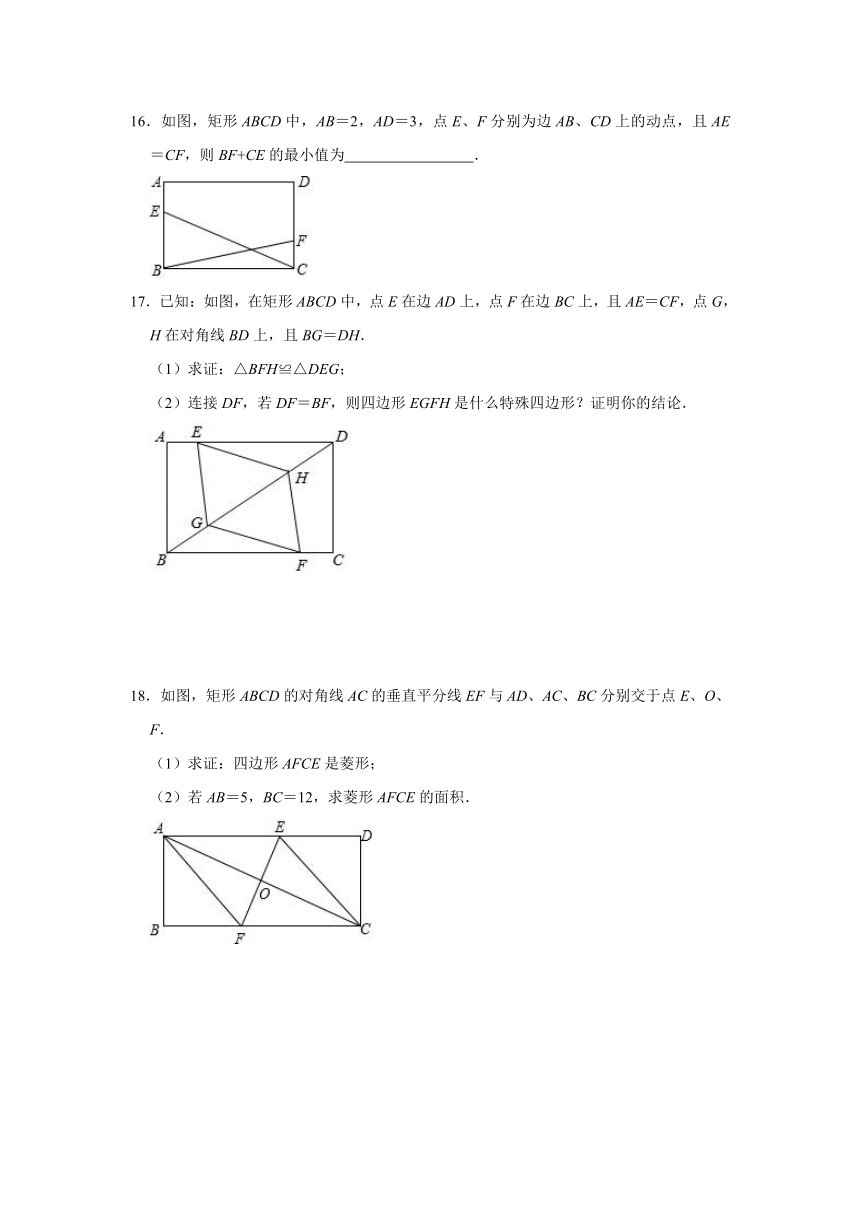
16.如图,矩形ABCD中,AB=2,AD=3,点E、F分别为边AB、CD上的动点,且AE=CF,则BF+CE的最小值为 .
17.已知:如图,在矩形ABCD中,点E在边AD上,点F在边BC上,且AE=CF,点G,H在对角线BD上,且BG=DH.
(1)求证:△BFH≌△DEG;
(2)连接DF,若DF=BF,则四边形EGFH是什么特殊四边形?证明你的结论.
18.如图,矩形ABCD的对角线AC的垂直平分线EF与AD、AC、BC分别交于点E、O、F.
(1)求证:四边形AFCE是菱形;
(2)若AB=5,BC=12,求菱形AFCE的面积.
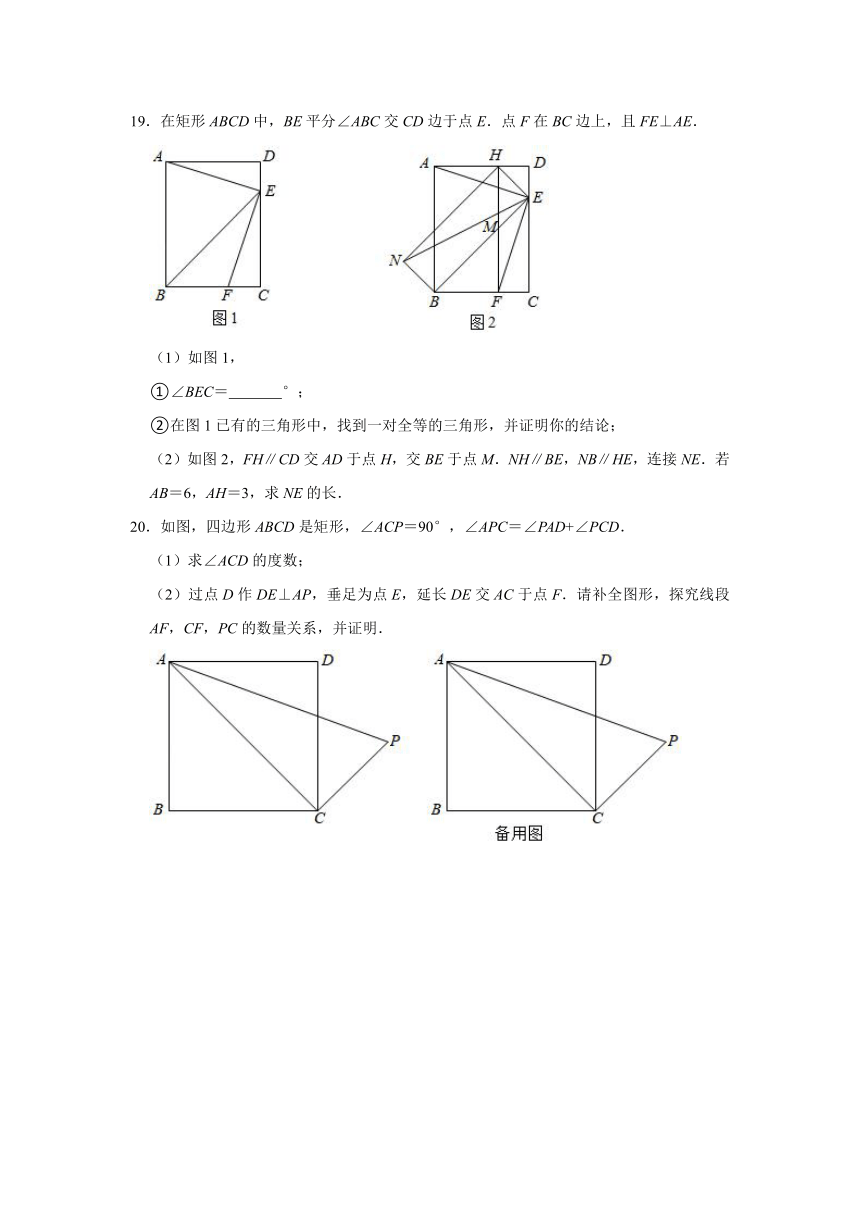
19.在矩形ABCD中,BE平分∠ABC交CD边于点E.点F在BC边上,且FE⊥AE.
(1)如图1,
①∠BEC= °;
②在图1已有的三角形中,找到一对全等的三角形,并证明你的结论;
(2)如图2,FH∥CD交AD于点H,交BE于点M.NH∥BE,NB∥HE,连接NE.若AB=6,AH=3,求NE的长.
20.如图,四边形ABCD是矩形,∠ACP=90°,∠APC=∠PAD+∠PCD.
(1)求∠ACD的度数;
(2)过点D作DE⊥AP,垂足为点E,延长DE交AC于点F.请补全图形,探究线段AF,CF,PC的数量关系,并证明.
参考答案
1.解:∵四边形ABCD的对角线互相平分,
∴四边形ABCD是平行四边形,
∵∠ABC=90°,
∴平行四边形ABCD是矩形,
故选:B.
2.解:根据平行四边形的性质可知:
①平行四边形的对角线互相平分,则OA=OC,故①正确;
②平行四边形的对角相等,则∠BAD=∠BCD,故②正确;
③平行四边形的邻角互补,则∠BAD+∠ABC=180°,故③正确;
④平行四边形的对角线互相平分,不一定垂直,故④错误;
⑤平行四边形对边相等,则AB=CD,故⑤正确;
故选:B.
3.解:连接AP,如图:
∵PE⊥AB,PF⊥AC,
∴∠AEP=∠AFP=90°,
∵∠BAC=90°,
∴四边形AFPE是矩形,
∴EF=AP,
要使EF最小,只要AP最小即可,
当AP⊥BC时,AP最短,
∵∠BAC=90°,AB=3,AC=4,
∴BC===5,
∵△ABC的面积=×4×3=×5×AP,
∴AP=2.4,
即EF=2.4,
故选:C.
4.解:∵DE∥AC,CE∥BD,
∴四边形OCED为平行四边形,
∵四边形ABCD是菱形,AC=12,BD=16,
∴AC⊥BD,OA=OC=AC=6,OB=OD=BD=8,
∴∠DOC=90°,CD===10,
∴平行四边形OCED为矩形,
∴OE=CD=10,
故选:C.
5.解:连接DH,并延长交EG于N,
∵AD∥EG,
∴∠DAH=∠AGN,
∵点H是AG的中点,
∴AH=HG,
在△ADH和△GNH中,
,
∴△ADH≌△GNH(ASA),
∴DH=HN,NG=AD=2,
∵AB=CD=EG=4,BC=CE=2,
∴DE=EN=2,
又∵∠DEN=90°,
∴DN=DE=2,
∵DE=EN,DH=HN,∠DEN=90°,
∴EH=DN=,
故选:A
6.解:连接PO,
∵矩形ABCD的两边AB=5,BC=12,
∴S矩形ABCD=AB?BC=60,OA=OC,OB=OD,AC=BD,AC===13,
∴S△AOD=S矩形ABCD=15,OA=OD=AC=,
∴S△AOD=S△AOP+S△DOP=OA?PE+OD?PF=OA(PE+PF)=××(PE+PF)=15,
∴PE+PF=,
故选:C.
7.解:
连接OB,过B作BM⊥x轴于M,
∵点B的坐标是(1,3),
∴OM=1,BM=3,由勾股定理得:OB==,
∵四边形OABC是矩形,
∴AC=OB,
∴AC=,
故选:C.
8.解:在由3×4个小正方形组成矩形ABCD中,
共有矩形60个,是正方形的有20个,
其中,边长为1的12个,边长为2的6个,边长为3的2个;
不是正方形的矩形有40个,
其中,两边长分别为2和1的有17个;
两边长分别为3和1的有10个;
两边长分别为4和1的有3个;
两边长分别为3和2的有7个;
两边长分别为3和4的有1个;
两边长分别为4和2的有2个;
故选:D.
9.解:∵AB=10,E为AB的中点,
∴AE=BE=5,
∵四边形ABCD是矩形,BC=3,
∴AD=BC=3,∠D=90°,
有三种情况:①AP=PE=5,作AE的垂直平分线MN,MN交AB于N,
此时P在AE的垂直平分线MN上,
即AN=NE=2.5,则DP=AN=2.5,
∵AD2+DP2=32+2.52≠52,
即此时不存在;
②当AP=AE=5时,由勾股定理得:DP===4;
③当PE=AE=5时,有P和P′两种情况,过P作PN⊥AB于N,
由勾股定理得:NE===4,
即DP=5﹣4=1;DP′=5+4=9,
所以DP的长是4或1或9,
故答案为:4或1或9.
10.解:延长OE,与BG交于M点,如图所示:
∵O为BF中点,EF∥BG,
∴OB=OF,∠EFO=MBO,
在△OEF和△OMB中,
∴△OEF≌△OMB(ASA),
∴EF=BM,OE=OM,
设EC=3x(0<3x<6),
则CG=EF=BM=4x,
∴MC=BC﹣BM=8﹣4x,
∴EM====,
当EM最小时,OE最小,此时x=,
即EC=3x=,
EM==,
∴OE=EM=.
故答案为:.
11.解:∵矩形ABCD中,BC=8,
∴AC==,
∴AO=AC,
∵对角线AC,BD交于点O,
∴△AOD的面积=矩形ABCD的面积=×AB?BC=2AB,
∵EO⊥AO,EF⊥DO,
∴S△AOD=S△AOE+S△DOE,
即2AB=AO×EO+DO×EF,
∴2AB=×AO(EO+EF)=AC×=AC,
∴2AB=,
∴5AB=3,
解得AB=6或AB=﹣6(舍去),
故答案为:6.
12.解:过点P作GH∥BC交AB、CD于点G、H,
过P作EF∥AB交AD、BC于点E、F,
设AE=BF=c,AG=DH=a,
GB=HC=b,ED=FC=d,
∴AP2=a2+c2,
CP2=b2+d2,
BP2=b2+c2,
DP2=d2+a2,
∵AP=1,BP=2,CP=3,
∴AP2+CP2=BP2+DP2,
1+9=4+DP2,
DP2=6,
DP=.
故答案为:.
13.解:如图,延长CF,BA交于点G,连接EF,过点F作FH⊥CE于H,过点E作EM⊥CF于M,
∵四边形ABCD是矩形,且AB=,BC=4,
∴AB∥CD,AB=CD=,∠D=∠ABC=∠CBE=90°,
∴∠DCF=∠G,
∵CF平分∠ECD,
∴∠DCF=∠FCE,FH=DF,
∴∠G=∠ECF,
∴EC=EG,
∴△ECG是等腰三角形,
∴CM=MG,
∵CE=CF,
∴△ECF是等腰三角形,
∵EM⊥CF,FH⊥CE,
∴EM和FH是等腰三角形腰上的高,
∴EM=FH=DF,
∴Rt△CDF≌Rt△CME(HL),
∴CM=CD=,
∴CG=5,
Rt△CBG中,BG===3,
设BE=x,则EC=EG=3+x,
Rt△CBE中,(3+x)2=x2+42,
解得:x=,
∴BE=.
故答案为:.
14.解:根据题意可知:
MN=CD,
∵四边形ABCD是矩形,
∴∠BAD=90°,DC⊥AD,CD=AB=6,
∴MF⊥AD,MN=6,
∵AF平分∠BAD,
∴∠BAF=∠DAF=45°,
∵AB=6,
∴AD=AB=6,
∵DF⊥AF,
∴△ADF是等腰直角三角形,
∴AF=DF,
∴点M是AD的中点,
∴FM=AD=3,FN为△BCH的中位线,
∴FN=MN﹣FM=6﹣3,FN=CH,
∴CH=2FN=12﹣6.
故答案为:12﹣6.
15.解:作PM⊥AD于M,交BC于N.
则有四边形AEPM,四边形DFPM,四边形CFPN,四边形BEPN都是矩形,
∴S△ADC=S△ABC,S△AMP=S△AEP,S△PBE=S△PBN,S△PFD=S△PDM,S△PFC=S△PCN,
∴S△DFP=S△PBE=×2×8=8,
∴S阴=8+8=16,
故答案为16
16.解:连接DE,
∵四边形ABCD是矩形,
∴AB=CD,
∵AE=CF,
∴BE=DF,
∴四边形BEDF是平行四边形,
∴DE=BF,
要求BF+CE的最小值,即求DE+CE的最小值,
作D点关于AB的对称点D′,连接D′C交AB于E,
则DE+CE=D′E+CE=CD′的值最小,
∵AB=2,AD=3,
∴CD=AB=2,DD′=2AD=6,
∴CD′===2,
即BF+CE的最小值为2,
故答案为:2.
17.(1)证明:∵四边形ABCD是矩形,
∴AD=BC,AD∥BC,
∴∠FBH=∠EDG,
∵AE=CF,BG=DH,
∴DE=BF,BH=DG,
在△BFH和△DEG中,,
∴△BFH≌△DEG(SAS);
(2)解:若DF=BF,则四边形EGFH是菱形;理由如下:
连接EF交GH于O,如图:
由(1)得:△BFH≌△DEG,
∴FH=EG,∠BHF=∠DGE,
∴FH∥EG,
∴四边形EGFH是平行四边形,
∴OG=OH,
∵BG=DH,
∴OB=OD,
∵DF=BF,
∴EF⊥GH,
∴四边形EGFH是菱形.
18.解:(1)∵四边形ABCD是矩形,
∴AE∥FC,
∴∠EAO=∠FCO,
∵EF垂直平分AC,
∴AO=CO,FE⊥AC,
又∠AOE=∠COF,
∴△AOE≌△COF(AAS),
∴EO=FO,
∴四边形AFCE为平行四边形,
又∵FE⊥AC,
∴平行四边形AFCE为菱形;
(2)在Rt△ABC中,由AB=5,BC=12,
根据勾股定理得:AC==13,
∴OA=,
∴EO=,
∴EF=
∴菱形AFCE的面积S=AC?EF=
19.解:(1)①∵四边形ABCD为矩形,
∴∠ABC=∠C=∠D=90°,AB∥CD,AD=BC.
∵BE平分∠ABC交CD边于点E,
∴∠ABE=∠CBE=∠ABC=45°,
∵AB∥CD,
∴∠BEC=∠ABE=45°.
故答案为:45.
②△ADE≌△ECF,
证明:∵∠CBE=∠BEC=45°,
∴BC=EC,
∵AD=BC,
∴AD=EC.
∵FE⊥AE,
∴∠AEF=90°,
∴∠DEA+∠CEF=90°,
又∵∠DAE+∠DEA=90°,
∴∠CEF=∠DAE.
在△ADE和△ECF中,
,
∴△ADE≌△ECF(ASA).
(2)在图2中,连接HB.
∵NH∥BE,NB∥HE,
∴四边形HNBE是平行四边形.
∵△ADE≌△ECF,
∴AE=EF,DE=CF.
∵四边形ABCD是矩形,
∴AD∥FC,∠D=90°.
∵FH∥CD,
∴四边形HFCD是平行四边形,
∴HD=FC,
∴HD=ED,∠D=90°,
∴∠DEH=45°.
又∵∠BEC=45°,
∴∠HEB=90°,
∴平行四边形HNBE是矩形,
∴NE=HB.
在Rt△ABH中,BH==3,
∴NE=3.
20.解:(1)∵四边形ABCD是矩形,
∴∠D=90°,
∴∠DAC+∠DCA=90°,
即∠DAP+∠PAC+∠DCA=90°,
∵∠ACP=90°,
∴∠APC+∠CAP=90°,
∵∠APC=∠PAD+∠PCD.
∴∠CAP+∠PAD+∠PCD=90°,
∴∠PCD=∠ACD,
∵∠ACP=90°,
∴∠PCD+∠ACD=90°,
∴∠ACD=45°;
(2)AF=CF+PC.
连接BD,交AC于点O,过点C作CN∥AP交BD于点N,如图.
证明:由(1)知,∠ACD=45°,
∴∠CAD=∠ACD=45°,
∴AD=CD,
∴矩形ABCD是正方形,
∴∠DAO=∠CDO=45°,∠AOD=90°,
∵∠ACP=∠AOD=90°,
∴MN∥PC,
∵AP∥CN,
∴∠1=∠2,四边形PCNM为平行四边形,
∴PC=MN,
∵∠1+∠3=90°,∠2+∠4=90°,
∴∠3=∠4,
在△ADF和△DCN中,
,
∴△ADF≌△DCN(AAS),
∴AF=DN,
∵∠7+∠ADE=90°,∠8+∠ADE=90°,
∴∠7=∠8,
在△ADM和△DCF中,
,
∴△ADM≌△DCF(ASA),
∴DM=CF,
∵AF=DN,PC=MN,
∴AF=DN=DM+MN=CF+PC.
1.如图,四边形ABCD的对角线互相平分,若∠ABC=90°,则四边形ABCD为( )
A.菱形 B.矩形 C.菱形或矩形 D.无法判断
2.如图平行四边形ABCD中,AC、BD相交于点O,下列结论:①OA=OC,②∠BAD=∠BCD,③∠BAD+∠ABC=180°,④AC⊥BD,⑤AB=CD,正确结论的个数是( )
A.5个 B.4个 C.3个 D.2个
3.如图,在△ABC中,∠BAC=90°,AB=3,AC=4,P为边BC上一动点,PE⊥AB于E,PF⊥AC于F,则EF的最小值为( )
A.1.2 B.1.25 C.2.4 D.2.5
4.如图,点O是菱形ABCD对角线的交点,DE∥AC,CE∥BD,连接OE,设AC=12,BD=16,则OE的长为( )
A.8 B.9 C.10 D.12
5.矩形ABCD与ECFG如图放置,点B,C,F共线,点C,E,D共线,连接AG,取AG的中点H,连接EH.若AB=CF=4,BC=CE=2,则EH=( )
A. B.2 C. D.
6.已知:如图,矩形ABCD中,AB=5,BC=12,对角线AC、BD相交于点O,点P是线段AD上任意一点,且PE⊥BD于点E,PF⊥AC于点F,则PE+PF等于( )
A. B. C. D.
7.如图,在矩形OABC中,点B的坐标是(1,3),则AC的长是( )
A.3 B.2 C. D.4
8.如图,矩形ABCD由3×4个小正方形组成,此图中不是正方形的矩形有( )
A.34个 B.36个 C.38个 D.40个
9.如图,在长方形ABCD中,AB=10,BC=3,点E是AB的中点,点P在边DC上运动,若△APE是腰长为5的等腰三角形,则DP的长为 .
10.如图,矩形ABCD中,BC=8,AB=6,点E为CD边上一动点(不与C,D重合).以CE为边向外作矩形CEFG,且CE:CG=3:4,连接BF,点O是线段BF的中点.连接OE,则OE的最小值为 .
11.如图,矩形ABCD的对角线AC,BD交于点O,过点O作OE⊥AC,交AD于点E,过点E作EF⊥BD,垂足为F,BC=8,OE+EF=,则线段AB的长为 .
12.已知矩形ABCD中有一点P,满足PA=1,PB=2,PC=3,则PD= .
13.在长方形ABCD中,AB=,BC=4,CE=CF,延长AB至点E,连接CE,CF平分∠ECD,则BE= .
14.如图,矩形ABCD中,AD=AB,AF平分∠BAD,DF⊥AF于点F,BF的延长线交CD于点H.过F作MN∥DC,交AD于M,交BC于N.若AB=6,则CH的长为 .
15.如图,点P是矩形ABCD的对角线AC上一点,过点P作EF∥BC,分别交AB,CD于点E,F,连接PB,PD.若AE=2,PF=8.则图中阴影部分的面积为 .
16.如图,矩形ABCD中,AB=2,AD=3,点E、F分别为边AB、CD上的动点,且AE=CF,则BF+CE的最小值为 .
17.已知:如图,在矩形ABCD中,点E在边AD上,点F在边BC上,且AE=CF,点G,H在对角线BD上,且BG=DH.
(1)求证:△BFH≌△DEG;
(2)连接DF,若DF=BF,则四边形EGFH是什么特殊四边形?证明你的结论.
18.如图,矩形ABCD的对角线AC的垂直平分线EF与AD、AC、BC分别交于点E、O、F.
(1)求证:四边形AFCE是菱形;
(2)若AB=5,BC=12,求菱形AFCE的面积.
19.在矩形ABCD中,BE平分∠ABC交CD边于点E.点F在BC边上,且FE⊥AE.
(1)如图1,
①∠BEC= °;
②在图1已有的三角形中,找到一对全等的三角形,并证明你的结论;
(2)如图2,FH∥CD交AD于点H,交BE于点M.NH∥BE,NB∥HE,连接NE.若AB=6,AH=3,求NE的长.
20.如图,四边形ABCD是矩形,∠ACP=90°,∠APC=∠PAD+∠PCD.
(1)求∠ACD的度数;
(2)过点D作DE⊥AP,垂足为点E,延长DE交AC于点F.请补全图形,探究线段AF,CF,PC的数量关系,并证明.
参考答案
1.解:∵四边形ABCD的对角线互相平分,
∴四边形ABCD是平行四边形,
∵∠ABC=90°,
∴平行四边形ABCD是矩形,
故选:B.
2.解:根据平行四边形的性质可知:
①平行四边形的对角线互相平分,则OA=OC,故①正确;
②平行四边形的对角相等,则∠BAD=∠BCD,故②正确;
③平行四边形的邻角互补,则∠BAD+∠ABC=180°,故③正确;
④平行四边形的对角线互相平分,不一定垂直,故④错误;
⑤平行四边形对边相等,则AB=CD,故⑤正确;
故选:B.
3.解:连接AP,如图:
∵PE⊥AB,PF⊥AC,
∴∠AEP=∠AFP=90°,
∵∠BAC=90°,
∴四边形AFPE是矩形,
∴EF=AP,
要使EF最小,只要AP最小即可,
当AP⊥BC时,AP最短,
∵∠BAC=90°,AB=3,AC=4,
∴BC===5,
∵△ABC的面积=×4×3=×5×AP,
∴AP=2.4,
即EF=2.4,
故选:C.
4.解:∵DE∥AC,CE∥BD,
∴四边形OCED为平行四边形,
∵四边形ABCD是菱形,AC=12,BD=16,
∴AC⊥BD,OA=OC=AC=6,OB=OD=BD=8,
∴∠DOC=90°,CD===10,
∴平行四边形OCED为矩形,
∴OE=CD=10,
故选:C.
5.解:连接DH,并延长交EG于N,
∵AD∥EG,
∴∠DAH=∠AGN,
∵点H是AG的中点,
∴AH=HG,
在△ADH和△GNH中,
,
∴△ADH≌△GNH(ASA),
∴DH=HN,NG=AD=2,
∵AB=CD=EG=4,BC=CE=2,
∴DE=EN=2,
又∵∠DEN=90°,
∴DN=DE=2,
∵DE=EN,DH=HN,∠DEN=90°,
∴EH=DN=,
故选:A
6.解:连接PO,
∵矩形ABCD的两边AB=5,BC=12,
∴S矩形ABCD=AB?BC=60,OA=OC,OB=OD,AC=BD,AC===13,
∴S△AOD=S矩形ABCD=15,OA=OD=AC=,
∴S△AOD=S△AOP+S△DOP=OA?PE+OD?PF=OA(PE+PF)=××(PE+PF)=15,
∴PE+PF=,
故选:C.
7.解:
连接OB,过B作BM⊥x轴于M,
∵点B的坐标是(1,3),
∴OM=1,BM=3,由勾股定理得:OB==,
∵四边形OABC是矩形,
∴AC=OB,
∴AC=,
故选:C.
8.解:在由3×4个小正方形组成矩形ABCD中,
共有矩形60个,是正方形的有20个,
其中,边长为1的12个,边长为2的6个,边长为3的2个;
不是正方形的矩形有40个,
其中,两边长分别为2和1的有17个;
两边长分别为3和1的有10个;
两边长分别为4和1的有3个;
两边长分别为3和2的有7个;
两边长分别为3和4的有1个;
两边长分别为4和2的有2个;
故选:D.
9.解:∵AB=10,E为AB的中点,
∴AE=BE=5,
∵四边形ABCD是矩形,BC=3,
∴AD=BC=3,∠D=90°,
有三种情况:①AP=PE=5,作AE的垂直平分线MN,MN交AB于N,
此时P在AE的垂直平分线MN上,
即AN=NE=2.5,则DP=AN=2.5,
∵AD2+DP2=32+2.52≠52,
即此时不存在;
②当AP=AE=5时,由勾股定理得:DP===4;
③当PE=AE=5时,有P和P′两种情况,过P作PN⊥AB于N,
由勾股定理得:NE===4,
即DP=5﹣4=1;DP′=5+4=9,
所以DP的长是4或1或9,
故答案为:4或1或9.
10.解:延长OE,与BG交于M点,如图所示:
∵O为BF中点,EF∥BG,
∴OB=OF,∠EFO=MBO,
在△OEF和△OMB中,
∴△OEF≌△OMB(ASA),
∴EF=BM,OE=OM,
设EC=3x(0<3x<6),
则CG=EF=BM=4x,
∴MC=BC﹣BM=8﹣4x,
∴EM====,
当EM最小时,OE最小,此时x=,
即EC=3x=,
EM==,
∴OE=EM=.
故答案为:.
11.解:∵矩形ABCD中,BC=8,
∴AC==,
∴AO=AC,
∵对角线AC,BD交于点O,
∴△AOD的面积=矩形ABCD的面积=×AB?BC=2AB,
∵EO⊥AO,EF⊥DO,
∴S△AOD=S△AOE+S△DOE,
即2AB=AO×EO+DO×EF,
∴2AB=×AO(EO+EF)=AC×=AC,
∴2AB=,
∴5AB=3,
解得AB=6或AB=﹣6(舍去),
故答案为:6.
12.解:过点P作GH∥BC交AB、CD于点G、H,
过P作EF∥AB交AD、BC于点E、F,
设AE=BF=c,AG=DH=a,
GB=HC=b,ED=FC=d,
∴AP2=a2+c2,
CP2=b2+d2,
BP2=b2+c2,
DP2=d2+a2,
∵AP=1,BP=2,CP=3,
∴AP2+CP2=BP2+DP2,
1+9=4+DP2,
DP2=6,
DP=.
故答案为:.
13.解:如图,延长CF,BA交于点G,连接EF,过点F作FH⊥CE于H,过点E作EM⊥CF于M,
∵四边形ABCD是矩形,且AB=,BC=4,
∴AB∥CD,AB=CD=,∠D=∠ABC=∠CBE=90°,
∴∠DCF=∠G,
∵CF平分∠ECD,
∴∠DCF=∠FCE,FH=DF,
∴∠G=∠ECF,
∴EC=EG,
∴△ECG是等腰三角形,
∴CM=MG,
∵CE=CF,
∴△ECF是等腰三角形,
∵EM⊥CF,FH⊥CE,
∴EM和FH是等腰三角形腰上的高,
∴EM=FH=DF,
∴Rt△CDF≌Rt△CME(HL),
∴CM=CD=,
∴CG=5,
Rt△CBG中,BG===3,
设BE=x,则EC=EG=3+x,
Rt△CBE中,(3+x)2=x2+42,
解得:x=,
∴BE=.
故答案为:.
14.解:根据题意可知:
MN=CD,
∵四边形ABCD是矩形,
∴∠BAD=90°,DC⊥AD,CD=AB=6,
∴MF⊥AD,MN=6,
∵AF平分∠BAD,
∴∠BAF=∠DAF=45°,
∵AB=6,
∴AD=AB=6,
∵DF⊥AF,
∴△ADF是等腰直角三角形,
∴AF=DF,
∴点M是AD的中点,
∴FM=AD=3,FN为△BCH的中位线,
∴FN=MN﹣FM=6﹣3,FN=CH,
∴CH=2FN=12﹣6.
故答案为:12﹣6.
15.解:作PM⊥AD于M,交BC于N.
则有四边形AEPM,四边形DFPM,四边形CFPN,四边形BEPN都是矩形,
∴S△ADC=S△ABC,S△AMP=S△AEP,S△PBE=S△PBN,S△PFD=S△PDM,S△PFC=S△PCN,
∴S△DFP=S△PBE=×2×8=8,
∴S阴=8+8=16,
故答案为16
16.解:连接DE,
∵四边形ABCD是矩形,
∴AB=CD,
∵AE=CF,
∴BE=DF,
∴四边形BEDF是平行四边形,
∴DE=BF,
要求BF+CE的最小值,即求DE+CE的最小值,
作D点关于AB的对称点D′,连接D′C交AB于E,
则DE+CE=D′E+CE=CD′的值最小,
∵AB=2,AD=3,
∴CD=AB=2,DD′=2AD=6,
∴CD′===2,
即BF+CE的最小值为2,
故答案为:2.
17.(1)证明:∵四边形ABCD是矩形,
∴AD=BC,AD∥BC,
∴∠FBH=∠EDG,
∵AE=CF,BG=DH,
∴DE=BF,BH=DG,
在△BFH和△DEG中,,
∴△BFH≌△DEG(SAS);
(2)解:若DF=BF,则四边形EGFH是菱形;理由如下:
连接EF交GH于O,如图:
由(1)得:△BFH≌△DEG,
∴FH=EG,∠BHF=∠DGE,
∴FH∥EG,
∴四边形EGFH是平行四边形,
∴OG=OH,
∵BG=DH,
∴OB=OD,
∵DF=BF,
∴EF⊥GH,
∴四边形EGFH是菱形.
18.解:(1)∵四边形ABCD是矩形,
∴AE∥FC,
∴∠EAO=∠FCO,
∵EF垂直平分AC,
∴AO=CO,FE⊥AC,
又∠AOE=∠COF,
∴△AOE≌△COF(AAS),
∴EO=FO,
∴四边形AFCE为平行四边形,
又∵FE⊥AC,
∴平行四边形AFCE为菱形;
(2)在Rt△ABC中,由AB=5,BC=12,
根据勾股定理得:AC==13,
∴OA=,
∴EO=,
∴EF=
∴菱形AFCE的面积S=AC?EF=
19.解:(1)①∵四边形ABCD为矩形,
∴∠ABC=∠C=∠D=90°,AB∥CD,AD=BC.
∵BE平分∠ABC交CD边于点E,
∴∠ABE=∠CBE=∠ABC=45°,
∵AB∥CD,
∴∠BEC=∠ABE=45°.
故答案为:45.
②△ADE≌△ECF,
证明:∵∠CBE=∠BEC=45°,
∴BC=EC,
∵AD=BC,
∴AD=EC.
∵FE⊥AE,
∴∠AEF=90°,
∴∠DEA+∠CEF=90°,
又∵∠DAE+∠DEA=90°,
∴∠CEF=∠DAE.
在△ADE和△ECF中,
,
∴△ADE≌△ECF(ASA).
(2)在图2中,连接HB.
∵NH∥BE,NB∥HE,
∴四边形HNBE是平行四边形.
∵△ADE≌△ECF,
∴AE=EF,DE=CF.
∵四边形ABCD是矩形,
∴AD∥FC,∠D=90°.
∵FH∥CD,
∴四边形HFCD是平行四边形,
∴HD=FC,
∴HD=ED,∠D=90°,
∴∠DEH=45°.
又∵∠BEC=45°,
∴∠HEB=90°,
∴平行四边形HNBE是矩形,
∴NE=HB.
在Rt△ABH中,BH==3,
∴NE=3.
20.解:(1)∵四边形ABCD是矩形,
∴∠D=90°,
∴∠DAC+∠DCA=90°,
即∠DAP+∠PAC+∠DCA=90°,
∵∠ACP=90°,
∴∠APC+∠CAP=90°,
∵∠APC=∠PAD+∠PCD.
∴∠CAP+∠PAD+∠PCD=90°,
∴∠PCD=∠ACD,
∵∠ACP=90°,
∴∠PCD+∠ACD=90°,
∴∠ACD=45°;
(2)AF=CF+PC.
连接BD,交AC于点O,过点C作CN∥AP交BD于点N,如图.
证明:由(1)知,∠ACD=45°,
∴∠CAD=∠ACD=45°,
∴AD=CD,
∴矩形ABCD是正方形,
∴∠DAO=∠CDO=45°,∠AOD=90°,
∵∠ACP=∠AOD=90°,
∴MN∥PC,
∵AP∥CN,
∴∠1=∠2,四边形PCNM为平行四边形,
∴PC=MN,
∵∠1+∠3=90°,∠2+∠4=90°,
∴∠3=∠4,
在△ADF和△DCN中,
,
∴△ADF≌△DCN(AAS),
∴AF=DN,
∵∠7+∠ADE=90°,∠8+∠ADE=90°,
∴∠7=∠8,
在△ADM和△DCF中,
,
∴△ADM≌△DCF(ASA),
∴DM=CF,
∵AF=DN,PC=MN,
∴AF=DN=DM+MN=CF+PC.
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
