《1.3正方形的性质与判定》同步能力达标训练(附解析)2021-2022学年九年级数学北师大版上册
文档属性
| 名称 | 《1.3正方形的性质与判定》同步能力达标训练(附解析)2021-2022学年九年级数学北师大版上册 |  | |
| 格式 | doc | ||
| 文件大小 | 291.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-07 13:23:26 | ||
图片预览



文档简介
2021年北师大版九年级数学上册《1.3正方形的性质与判定》同步能力达标训练(附答案)
1.如图,正方形ABCD的对角线AC,BD交于点O,M是边AD上一点,连接OM,过点O作ON⊥OM,交CD于点N.若四边形MOND的面积是1,则AB的长为( )
A.1 B. C.2 D.2
2.如图的正三角形ABC与正方形CDEF中,B、C、D三点共线,且AC=10,CF=8.若有一动点P沿着CA由C往A移动,则FP的长度最小为多少?( )
A.4 B.5 C.4 D.5
3.如图,在边长为2的正方形EFGH中,M,N分别为EF与GH的中点,一个三角形ABC沿竖直方向向上平移,在运动的过程中,点A恒在直线MN上,当点A运动到线段MN的中点时,点E,F恰与AB,AC两边的中点重合,设点A到EF的距离为x,三角形ABC与正方形EFGH的公共部分的面积为y.则当y=时,x的值为( )
A.或2+ B.或2﹣ C.2± D.或
4.下列说法正确的是( )
A.一组对边平行另一组对边相等的四边形是平行四边形
B.对角线互相垂直平分的四边形是菱形
C.对角线相等的四边形是矩形
D.对角线互相垂直且相等的四边形是正方形
5.如图是以正方形的边长为直径,在正方形内画半圆得到的图形,则此图形的对称轴有( )
A.2条 B.4条 C.6条 D.8条
6.如图,在正方形ABCD中,点E、F分别在CD、BC上(不与端点重合),且BF=CE,连接BE、AF相交于点G,则下列结论不正确的是( )
A.BE=AF B.∠AFB+∠BEC=90°
C.∠DAF=∠ABE D.AG⊥BE
7.如图,四边形OBCD是正方形,O,D两点的坐标分别是(0,0),(0,6),点C在第一象限,则点C的坐标是( )
A.(6,3) B.(3,6) C.(0,6) D.(6,6)
8.已知四边形ABCD是平行四边形,AC,BD相交于点O,下列结论错误的是( )
A.OA=OC,OB=OD
B.当AB=CD时,四边形ABCD是菱形
C.当∠ABC=90°时,四边形ABCD是矩形
D.当AC=BD且AC⊥BD时,四边形ABCD是正方形
9.如图,在△ABC中,∠ACB=90°,边BC在x轴上,顶点A,B的坐标分别为(﹣2,6)和(7,0).将正方形OCDE沿x轴向右平移,当点E落在AB边上时,点D的坐标为( )
A.(,2) B.(2,2) C.(,2) D.(4,2)
10.下列是关于某个四边形的三个结论:①它的对角线相等;②它是一个正方形;③它是一个矩形.下列推理过程正确的是( )
A.由②推出③,由③推出① B.由①推出②,由②推出③
C.由③推出①,由①推出② D.由①推出③,由③推出②
11.如图,正方形ABCD的边长为4,对角线AC,BD相交于点O,点E,F分别在BC,CD的延长线上,且CE=2,DF=1,G为EF的中点,连接OE,交CD于点H,连接GH,则GH的长为 .
12.已知△ABC的三个顶点都是同一个正方形的顶点,∠ABC的平分线与线段AC交于点D.若△ABC的一条边长为6,则点D到直线AB的距离为 .
13.如图,正方形ABCD中,点E、F分别在BC、CD上,△AEF是等边三角形,连接AC交EF于G,下列结论:①BE=DF;②∠DAF=15°,③AC垂直平分EF,④,其中正确结论有 个.
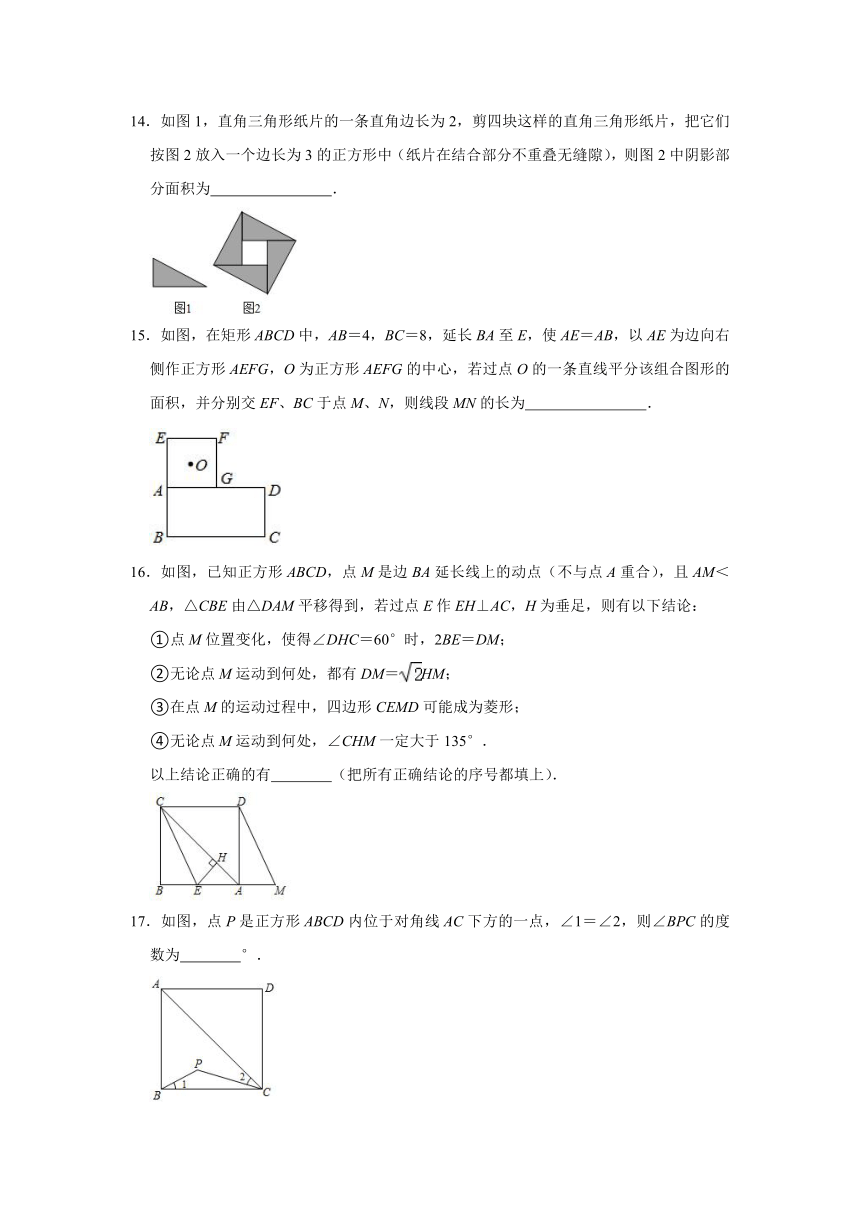
14.如图1,直角三角形纸片的一条直角边长为2,剪四块这样的直角三角形纸片,把它们按图2放入一个边长为3的正方形中(纸片在结合部分不重叠无缝隙),则图2中阴影部分面积为 .
15.如图,在矩形ABCD中,AB=4,BC=8,延长BA至E,使AE=AB,以AE为边向右侧作正方形AEFG,O为正方形AEFG的中心,若过点O的一条直线平分该组合图形的面积,并分别交EF、BC于点M、N,则线段MN的长为 .
16.如图,已知正方形ABCD,点M是边BA延长线上的动点(不与点A重合),且AM<AB,△CBE由△DAM平移得到,若过点E作EH⊥AC,H为垂足,则有以下结论:
①点M位置变化,使得∠DHC=60°时,2BE=DM;
②无论点M运动到何处,都有DM=HM;
③在点M的运动过程中,四边形CEMD可能成为菱形;
④无论点M运动到何处,∠CHM一定大于135°.
以上结论正确的有 (把所有正确结论的序号都填上).
17.如图,点P是正方形ABCD内位于对角线AC下方的一点,∠1=∠2,则∠BPC的度数为 °.
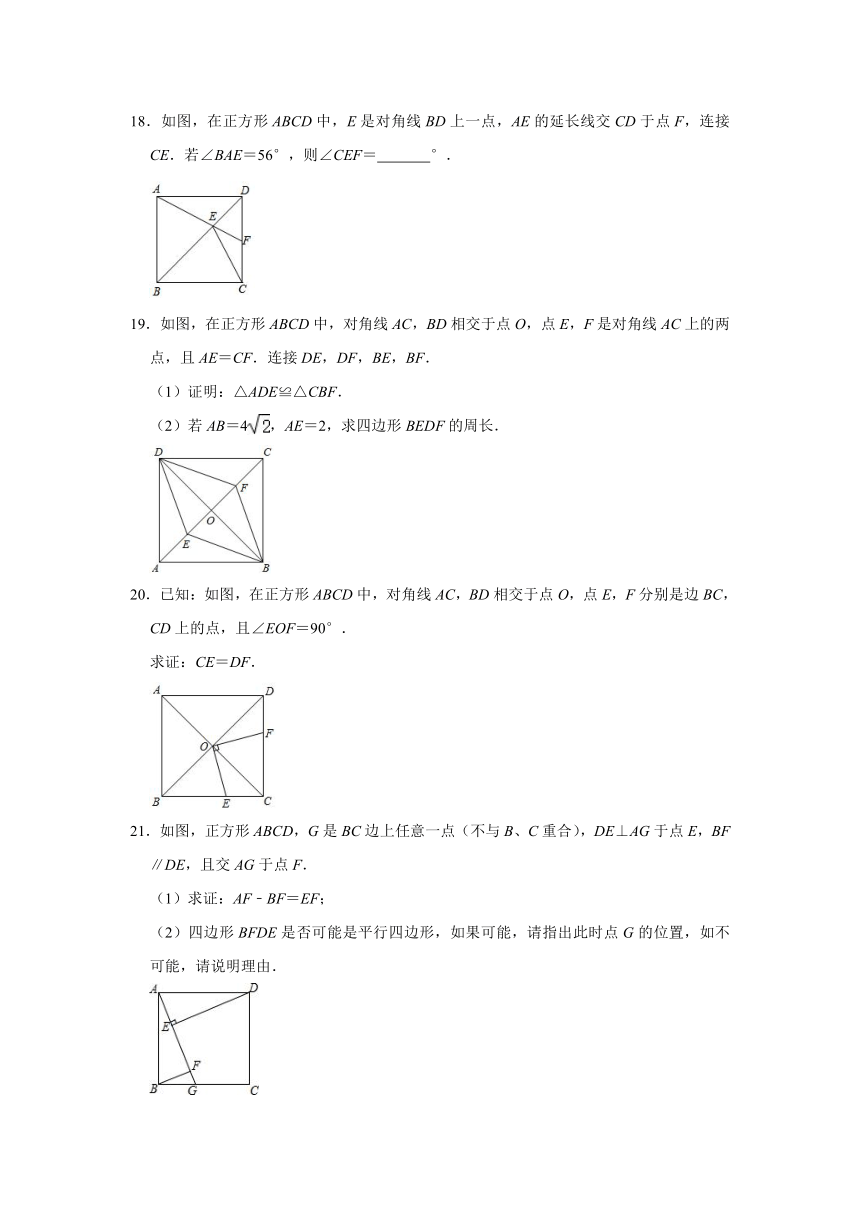
18.如图,在正方形ABCD中,E是对角线BD上一点,AE的延长线交CD于点F,连接CE.若∠BAE=56°,则∠CEF= °.
19.如图,在正方形ABCD中,对角线AC,BD相交于点O,点E,F是对角线AC上的两点,且AE=CF.连接DE,DF,BE,BF.
(1)证明:△ADE≌△CBF.
(2)若AB=4,AE=2,求四边形BEDF的周长.
20.已知:如图,在正方形ABCD中,对角线AC,BD相交于点O,点E,F分别是边BC,CD上的点,且∠EOF=90°.
求证:CE=DF.
21.如图,正方形ABCD,G是BC边上任意一点(不与B、C重合),DE⊥AG于点E,BF∥DE,且交AG于点F.
(1)求证:AF﹣BF=EF;
(2)四边形BFDE是否可能是平行四边形,如果可能,请指出此时点G的位置,如不可能,请说明理由.
22.如图,在正方形ABCD中,点E在BC边的延长线上,点F在CD边的延长线上,且CE=DF,连接AE和BF相交于点M.
求证:AE=BF.
23.如图,正方形ABCD的边CD在正方形ECGF的边CE上,连接DG,过点A作AH∥DG,交BG于点H.连接HF,AF,其中AF交EC于点M.
求证:△AHF为等腰直角三角形.
24.如图,在正方形ABCD中,点E是BC上的一点,点F是CD延长线上的一点,且BE=DF,连接AE、AF、EF.
(1)求证:△ABE≌△ADF;
(2)若AE=5,请求出EF的长.
25.如图,E,F分别是正方形ABCD的边CB,DC延长线上的点,且BE=CF,过点E作EG∥BF,交正方形外角的平分线CG于点G,连接GF.求证:
(1)AE⊥BF;
(2)四边形BEGF是平行四边形.
参考答案
1.解:∵四边形ABCD是正方形,
∴∠MDO=∠NCO=45°,OD=OC,∠DOC=90°,
∴∠DON+∠CON=90°,
∵ON⊥OM,
∴∠MON=90°,
∴∠DON+∠DOM=90°,
∴∠DOM=∠CON,
在△DOM和△CON中,
,
∴△DOM≌△CON(ASA),
∵四边形MOND的面积是1,四边形MOND的面积=△DOM的面积+△DON的面积,
∴四边形MOND的面积=△CON的面积+△DON的面积=△DOC的面积,
∴△DOC的面积是1,
∴正方形ABCD的面积是4,
∵AB2=4,
∴AB=2,
故选:C.
2.解:如图,
过点F,作FM⊥AC交AC于点M,
此时FM为FP的最小值,
∵∠ACD=60°,∠FCD=90°,
∴∠FCM=180°﹣∠ACB﹣∠FCD
=180°﹣60°﹣90°
=30°,
又∵∠FMC=90°,
∴MF=FC=4,
即PF的长度最小值为4,
故选:A.
3.解:如图1中,当过A在正方形内部时,连接EG交MN于O,连接OF,设AB交EH于Q,AC交FG于P.
由题意,△ABC是等腰直角三角形,AQ=OE=OG=AP=OF,S△OEF=1,
∵y=,
∴S四边形AOEQ+S四边形AOFP=1.5,
∴OA?2=1.5,
∴OA=,
∴AM=1+=.
如图2中,当点A在正方形外部时,
由题意,重叠部分是六边形WQRJPT,S重叠=S△ABC﹣2S△BQR﹣S△AWT,
∴2.5=××﹣1﹣×2AN×AN,
解得AN=,
∴AM=2+,
综上所述,满足条件的AM的值为或2+,
故选:A.
4.解:A、一组对边平行另一组对边相等的四边形可以是等腰梯形,可以是平行四边形,故选项A不合题意;
B、对角线互相垂直平分的四边形是菱形,故选项B符合题意;
C、对角线相等的平行四边形是矩形,故选项C不合题意;
D、对角线互相垂直平分且相等的四边形是正方形,故选项D不合题意;
故选:B.
5.解:如图,
因为以正方形的边长为直径,在正方形内画半圆得到的图形,
所以此图形的对称轴有4条.
故选:B.
6.解:∵ABCD是正方形,
∴∠ABF=∠C=90°,AB=BC,
∵BF=CE,
∴△ABF≌△BCE(SAS),
∴AF=BE(A正确),∠BAF=∠CBE,∠AFB=∠BEC(B错误),
∵∠BAF+∠DAF=90°,∠ABE+∠EBC=90°,
∴∠DAF=∠ABE(C正确),
∵∠BAF=∠CBE,∠BAF+∠AFB=90°,
∴∠CBE+∠AFB=90°,
∴AG⊥BE(第四个正确),
所以不正确的是B,
故选:B.
7.解:∵四边形OBCD是正方形,
∴OB=BC=CD=OD,∠CDO=∠CBO=90°,
∵O,D两点的坐标分别是(0,0),(0,6),
∴OD=6,
∴OB=BC=CD=6,
∴C(6,6).
故选:D.
8.解:A、根据平行四边形的性质得到OA=OC,OB=OD,该结论正确;
B、当AB=CD时,四边形ABCD还是平行四边形,该选项错误;
C、根据有一个角是直角的平行四边形是矩形可以判断该选项正确;
D、当AC=BD且AC⊥BD时,根据对角线相等可判断四边形ABCD是矩形,根据对角线互相垂直可判断四边形ABCD 是菱形,故四边形ABCD是正方形,该结论正确;
故选:B.
9.解:设直线AB的解析式为y=kx+b,
∵顶点A,B的坐标分别为(﹣2,6)和(7,0).
∴,
∴,
∴,
∵∠ACB=90°,边BC在x轴上,∴C点的坐标为(﹣2,0),
∴正方形OCDE的边长为2,
∴E(0,2),设点E沿x轴平移后落在AB边上的坐标为(a,2),
由y=﹣得,2=﹣a+,
∴a=4,
∴当点E落在AB边上时,点D的坐标为(2,2),
故选:B.
10.解:对角线相等的四边形推不出是正方形或矩形,
故①→②,①→③错误,
故选项B,C,D错误,
故选:A.
11.解:以O为原点,垂直AB的直线为x轴,建立直角坐标系,如图:
∵正方形ABCD的边长为4,CE=2,DF=1,
∴E(4,﹣2),F(2,3),
∵G为EF的中点,
∴G(3,),
设直线OE解析式为y=kx,将E(4,﹣2)代入得:
﹣2=4k,解得k=﹣,
∴直线OE解析式为y=﹣x,
令x=2得y=﹣1,
∴H(2,﹣1),
∴GH==,
方法二:如下图,连接OF,过点O作OM⊥CD交CD于M,
∵O为正方形对角线AC和BD的交点,
∴OM=CM=DM=CE=2,易证△OHM≌△EHC,
∴点H、点G分别为OE、FE的中点,
∴GH为△OEF的中位线,
∴GH=OF,
在Rt△OMF中,由勾股定理可得OF===,
∴GH=OF=,
故答案为:.
12.解:①当B为直角顶点时,过D作DH⊥AB于H,如图:
∵△ABC的三个顶点都是同一个正方形的顶点,∠ABC的平分线与线段AC交于点D,
∴△ABC是等腰直角三角形,∠ABD=∠ADH=45°,AD=CD=AC,
∴△AHD和△BHD是等腰直角三角形,
∴AH=DH=BH,
∴DH=BC,
若AC=6,则BC=3,此时DH=,即点D到直线AB的距离为;
若AB=BC=6,则DH=BC=3,即点D到直线AB的距离为3;
②当B不是直角顶点时,过D作DH⊥BC于H,如图:
∵△ABC的三个顶点都是同一个正方形的顶点,∠ABC的平分线与线段AC交于点D,
∴△CDH是等腰直角三角,AD=DH=CH,
在△ABD和△HBD中,
,
∴△ABD≌△HBD(AAS),
∴AB=BH,
若AB=AC=6时,BH=6,BC==6,
∴CH=BC﹣BH=6﹣6,
∴AD=6﹣6,即此时点D到直线AB的距离为6﹣6;
若BC=6,则AB=3,
∴BH=3,
∴CH=6﹣3,
∴AD=6﹣3,即此时点D到直线AB的距离为6﹣3;
综上所述,点D到直线AB的距离为或3或6﹣6或6﹣3.
故答案为:或3或6﹣6或6﹣3.
13.解:∵四边形ABCD是正方形,
∴AB=BC=CD=AD,∠B=∠BCD=∠D=∠BAD=90°,
∵△AEF等边三角形,
∴AE=EF=AF,∠EAF=60°,
∴∠BAE+∠DAF=30°,
在Rt△ABE和Rt△ADF中,
,
∴Rt△ABE≌Rt△ADF(HL),
∴BE=DF,∠BAE=∠DAF,
故①正确;
∵∠BAE+∠DAF=30°,
∴∠DAF+∠DAF=30°,
即∠DAF=15°,
故②正确;
∵BC=CD,
∴BC﹣BE=CD﹣DF,即CE=CF,
∵Rt△ABE≌Rt△ADF,
∴AE=AF,
∴AC垂直平分EF,
∴EG=FG,
故③正确;
∵∠ECF=90°,EG=FG,
∴CG=EF,
设EC=FC=x,由勾股定理,得EF==x,
∴CG=EF=x=CE,
故④正确;
综上所述,正确的有①②③④,共4个
14.解:由题意可得,
直角三角形的斜边长为3,一条直角边长为2,
故直角三角形的另一条直角边长为:=,
故阴影部分的面积是:=4,
故答案为:4.
15.解:如图,连接AC,BD交于点H,过点O和点H的直线MN平分该组合图形的面积,交AD于S,取AE中点P,取AB中点Q,连接OP,HQ,过点O作OT⊥QH于T,
∵四边形ABCD是矩形,
∴AH=HC,
又∵Q是AB中点,
∴QH=BC=4,QH∥BC,AQ=BQ=2,
同理可求PO=AG=2,PO∥AG,EP=AP=2,
∴PO∥AD∥BC∥EF∥QH,EP=AP=AQ=BQ,
∴MO=OS=SH=NH,∠OPQ=∠PQH=90°,
∵OT⊥QH,
∴四边形POTQ是矩形,
∴PO=QT=2,OT=PQ=4,
∴TH=2,
∴OH===2,
∴MN=2OH=4,
故答案为:4.
16.解:如图,连接DH,HM.
由题可得,AM=BE,
∴AB=EM=AD,
∵四边形ABCD是正方形,EH⊥AC,
∴EM=AD,∠AHE=90°,∠MEH=∠DAH=45°=∠EAH,
∴EH=AH,
∴△MEH≌△DAH(SAS),
∴∠MHE=∠DHA,MH=DH,
∴∠MHD=∠AHE=90°,△DHM是等腰直角三角形,
∴DM=HM,故②正确;
当∠DHC=60°时,∠ADH=60°﹣45°=15°,
∴∠ADM=45°﹣15°=30°,
∴Rt△ADM中,DM=2AM,
即DM=2BE,故①正确;
∵CD∥EM,EC∥DM,
∴四边形CEMD是平行四边形,
∵DM>AD,AD=CD,
∴DM>CD,
∴四边形CEMD不可能是菱形,故③错误,
∵点M是边BA延长线上的动点(不与点A重合),且AM<AB,
∴∠AHM<∠BAC=45°,
∴∠CHM>135°,故④正确;
由上可得正确结论的序号为①②④.
故答案为①②④.
17.解:∵四边形ABCD是正方形,
∴∠ACB=∠BAC=45°,
∴∠2+∠BCP=45°,
∵∠1=∠2,
∴∠1+∠BCP=45°,
∵∠BPC=180°﹣∠1﹣∠BCP,
∴∠BPC=135°,
故答案为:135.
18.解:∵正方形ABCD中,∠BAD=∠ADF=90°,∠BAE=56°,
∴∠DAF=34°,∠DFE=56°,
∵AD=CD,∠ADE=∠CDE,DE=DE,
∴△ADE≌△CDE(SAS),
∴∠DCE=∠DAF=34°,
∵∠DFE是△CEF的外角,
∴∠CEF=∠DFE﹣∠DCE=56°﹣34°=22°,
故答案为:22.
19.解;(1)证明:由正方形对角线平分每一组对角可知:∠DAE=∠BCF=45°,
在△ADE和△CBF中,
,
∴△ADE≌△CBF(SAS).
(2)∵AB=AD=,
∴BD===8,
由正方形对角线相等且互相垂直平分可得:AC=BD=8,DO=BO=4,OA=OC=4,
又AE=CF=2,
∴OA﹣AE=OC﹣CF,
即OE=OF=4﹣2=2,
故四边形BEDF为菱形.
∵∠DOE=90°,
∴DE===2.
∴4DE=
故四边形BEDF的周长为8.
20.证明:∵四边形ABCD为正方形,
∴OD=OC,∠ODF=∠OCE=45°,∠COD=90°,
∴∠DOF+∠COF=90°,
∵∠EOF=90°,即∠COE+∠COF=90°,
∴∠COE=∠DOF,
∴△COE≌△DOF(ASA),
∴CE=DF.
21.解:(1)证明:∵四边形ABCD是正方形,
∴AB=AD,∠BAF+∠DAE=90°,
∵DE⊥AG,
∴∠DAE+∠ADE=90°,
∴∠ADE=∠BAF,
又∵BF∥DE,
∴∠BFA=90°=∠AED,
∴△ABF≌△DAE(AAS),
∴AE=BF,
∴AF﹣BF=AF﹣AE=EF;
(2)不可能,理由是:
如图,若要四边形BFDE是平行四边形,
已知DE∥BF,则当DE=BF时,四边形BFDE为平行四边形,
∵DE=AF,
∴BF=AF,即此时∠BAF=45°,
而点G不与B和C重合,
∴∠BAF≠45°,矛盾,
∴四边形BFDE不可能是平行四边形.
22.解:证明:在正方形ABCD中,
AB=BC=CD=DA,∠ABE=∠BCF=90°,
∵CE=DF,
∴BE=CF,
在△AEB与△BFC中,
,
∴△AEB≌△BFC(SAS),
∴AE=BF.
23.证明:∵四边形ABCD,四边形ECGF都是正方形
∴DA∥BC,AD=CD,FG=CG,∠B=∠CGF=90°
∵AD∥BC,AH∥DG
∴四边形AHGD是平行四边形
∴AH=DG,AD=HG=CD
∵CD=HG,∠ECG=∠CGF=90°,FG=CG
∴△DCG≌△HGF(SAS)
∴DG=HF,∠HFG=∠HGD
∴AH=HF,
∵∠HGD+∠DGF=90°
∴∠HFG+∠DGF=90°
∴DG⊥HF,且AH∥DG
∴AH⊥HF,且AH=HF
∴△AHF为等腰直角三角形.
24.(1)证明:∵四边形ABCD是正方形,
∴AB=AD,∠ABC=∠ADC=∠ADF=90°,
在△ABE和△ADF中,
,
∴△ABE≌△ADF(SAS);
(2)解:∵△ABE≌△ADF,
∴AE=AF,∠BAE=∠DAF,
∵∠BAE+∠EAD=90°,
∴∠DAF+∠EAD=90°,即∠EAF=90°,
∴EF=AE=5.
25.证明:(1)∵四边形ABCD是正方形,
∴AB=BC,∠ABC=∠BCD=90°,
∴∠ABE=∠BCF=90°,
在△ABE和△BCF中,,
∴△ABE≌△BCF(SAS),
∴AE=BF,∠BAE=∠CBF,
∵EG∥BF,
∴∠CBF=∠CEG,
∵∠BAE+∠BEA=90°,
∴∠CEG+∠BEA=90°,
∴AE⊥EG,
∴AE⊥BF;
(2)延长AB至点P,使BP=BE,连接EP,如图所示:
则AP=CE,∠EBP=90°,
∴∠P=45°,
∵CG为正方形ABCD外角的平分线,
∴∠ECG=45°,
∴∠P=∠ECG,
由(1)得∠BAE=∠CEG,
在△APE和△ECG中,,
∴△APE≌△ECG(ASA),
∴AE=EG,
∵AE=BF,
∴EG=BF,
∵EG∥BF,
∴四边形BEGF是平行四边形.
1.如图,正方形ABCD的对角线AC,BD交于点O,M是边AD上一点,连接OM,过点O作ON⊥OM,交CD于点N.若四边形MOND的面积是1,则AB的长为( )
A.1 B. C.2 D.2
2.如图的正三角形ABC与正方形CDEF中,B、C、D三点共线,且AC=10,CF=8.若有一动点P沿着CA由C往A移动,则FP的长度最小为多少?( )
A.4 B.5 C.4 D.5
3.如图,在边长为2的正方形EFGH中,M,N分别为EF与GH的中点,一个三角形ABC沿竖直方向向上平移,在运动的过程中,点A恒在直线MN上,当点A运动到线段MN的中点时,点E,F恰与AB,AC两边的中点重合,设点A到EF的距离为x,三角形ABC与正方形EFGH的公共部分的面积为y.则当y=时,x的值为( )
A.或2+ B.或2﹣ C.2± D.或
4.下列说法正确的是( )
A.一组对边平行另一组对边相等的四边形是平行四边形
B.对角线互相垂直平分的四边形是菱形
C.对角线相等的四边形是矩形
D.对角线互相垂直且相等的四边形是正方形
5.如图是以正方形的边长为直径,在正方形内画半圆得到的图形,则此图形的对称轴有( )
A.2条 B.4条 C.6条 D.8条
6.如图,在正方形ABCD中,点E、F分别在CD、BC上(不与端点重合),且BF=CE,连接BE、AF相交于点G,则下列结论不正确的是( )
A.BE=AF B.∠AFB+∠BEC=90°
C.∠DAF=∠ABE D.AG⊥BE
7.如图,四边形OBCD是正方形,O,D两点的坐标分别是(0,0),(0,6),点C在第一象限,则点C的坐标是( )
A.(6,3) B.(3,6) C.(0,6) D.(6,6)
8.已知四边形ABCD是平行四边形,AC,BD相交于点O,下列结论错误的是( )
A.OA=OC,OB=OD
B.当AB=CD时,四边形ABCD是菱形
C.当∠ABC=90°时,四边形ABCD是矩形
D.当AC=BD且AC⊥BD时,四边形ABCD是正方形
9.如图,在△ABC中,∠ACB=90°,边BC在x轴上,顶点A,B的坐标分别为(﹣2,6)和(7,0).将正方形OCDE沿x轴向右平移,当点E落在AB边上时,点D的坐标为( )
A.(,2) B.(2,2) C.(,2) D.(4,2)
10.下列是关于某个四边形的三个结论:①它的对角线相等;②它是一个正方形;③它是一个矩形.下列推理过程正确的是( )
A.由②推出③,由③推出① B.由①推出②,由②推出③
C.由③推出①,由①推出② D.由①推出③,由③推出②
11.如图,正方形ABCD的边长为4,对角线AC,BD相交于点O,点E,F分别在BC,CD的延长线上,且CE=2,DF=1,G为EF的中点,连接OE,交CD于点H,连接GH,则GH的长为 .
12.已知△ABC的三个顶点都是同一个正方形的顶点,∠ABC的平分线与线段AC交于点D.若△ABC的一条边长为6,则点D到直线AB的距离为 .
13.如图,正方形ABCD中,点E、F分别在BC、CD上,△AEF是等边三角形,连接AC交EF于G,下列结论:①BE=DF;②∠DAF=15°,③AC垂直平分EF,④,其中正确结论有 个.
14.如图1,直角三角形纸片的一条直角边长为2,剪四块这样的直角三角形纸片,把它们按图2放入一个边长为3的正方形中(纸片在结合部分不重叠无缝隙),则图2中阴影部分面积为 .
15.如图,在矩形ABCD中,AB=4,BC=8,延长BA至E,使AE=AB,以AE为边向右侧作正方形AEFG,O为正方形AEFG的中心,若过点O的一条直线平分该组合图形的面积,并分别交EF、BC于点M、N,则线段MN的长为 .
16.如图,已知正方形ABCD,点M是边BA延长线上的动点(不与点A重合),且AM<AB,△CBE由△DAM平移得到,若过点E作EH⊥AC,H为垂足,则有以下结论:
①点M位置变化,使得∠DHC=60°时,2BE=DM;
②无论点M运动到何处,都有DM=HM;
③在点M的运动过程中,四边形CEMD可能成为菱形;
④无论点M运动到何处,∠CHM一定大于135°.
以上结论正确的有 (把所有正确结论的序号都填上).
17.如图,点P是正方形ABCD内位于对角线AC下方的一点,∠1=∠2,则∠BPC的度数为 °.
18.如图,在正方形ABCD中,E是对角线BD上一点,AE的延长线交CD于点F,连接CE.若∠BAE=56°,则∠CEF= °.
19.如图,在正方形ABCD中,对角线AC,BD相交于点O,点E,F是对角线AC上的两点,且AE=CF.连接DE,DF,BE,BF.
(1)证明:△ADE≌△CBF.
(2)若AB=4,AE=2,求四边形BEDF的周长.
20.已知:如图,在正方形ABCD中,对角线AC,BD相交于点O,点E,F分别是边BC,CD上的点,且∠EOF=90°.
求证:CE=DF.
21.如图,正方形ABCD,G是BC边上任意一点(不与B、C重合),DE⊥AG于点E,BF∥DE,且交AG于点F.
(1)求证:AF﹣BF=EF;
(2)四边形BFDE是否可能是平行四边形,如果可能,请指出此时点G的位置,如不可能,请说明理由.
22.如图,在正方形ABCD中,点E在BC边的延长线上,点F在CD边的延长线上,且CE=DF,连接AE和BF相交于点M.
求证:AE=BF.
23.如图,正方形ABCD的边CD在正方形ECGF的边CE上,连接DG,过点A作AH∥DG,交BG于点H.连接HF,AF,其中AF交EC于点M.
求证:△AHF为等腰直角三角形.
24.如图,在正方形ABCD中,点E是BC上的一点,点F是CD延长线上的一点,且BE=DF,连接AE、AF、EF.
(1)求证:△ABE≌△ADF;
(2)若AE=5,请求出EF的长.
25.如图,E,F分别是正方形ABCD的边CB,DC延长线上的点,且BE=CF,过点E作EG∥BF,交正方形外角的平分线CG于点G,连接GF.求证:
(1)AE⊥BF;
(2)四边形BEGF是平行四边形.
参考答案
1.解:∵四边形ABCD是正方形,
∴∠MDO=∠NCO=45°,OD=OC,∠DOC=90°,
∴∠DON+∠CON=90°,
∵ON⊥OM,
∴∠MON=90°,
∴∠DON+∠DOM=90°,
∴∠DOM=∠CON,
在△DOM和△CON中,
,
∴△DOM≌△CON(ASA),
∵四边形MOND的面积是1,四边形MOND的面积=△DOM的面积+△DON的面积,
∴四边形MOND的面积=△CON的面积+△DON的面积=△DOC的面积,
∴△DOC的面积是1,
∴正方形ABCD的面积是4,
∵AB2=4,
∴AB=2,
故选:C.
2.解:如图,
过点F,作FM⊥AC交AC于点M,
此时FM为FP的最小值,
∵∠ACD=60°,∠FCD=90°,
∴∠FCM=180°﹣∠ACB﹣∠FCD
=180°﹣60°﹣90°
=30°,
又∵∠FMC=90°,
∴MF=FC=4,
即PF的长度最小值为4,
故选:A.
3.解:如图1中,当过A在正方形内部时,连接EG交MN于O,连接OF,设AB交EH于Q,AC交FG于P.
由题意,△ABC是等腰直角三角形,AQ=OE=OG=AP=OF,S△OEF=1,
∵y=,
∴S四边形AOEQ+S四边形AOFP=1.5,
∴OA?2=1.5,
∴OA=,
∴AM=1+=.
如图2中,当点A在正方形外部时,
由题意,重叠部分是六边形WQRJPT,S重叠=S△ABC﹣2S△BQR﹣S△AWT,
∴2.5=××﹣1﹣×2AN×AN,
解得AN=,
∴AM=2+,
综上所述,满足条件的AM的值为或2+,
故选:A.
4.解:A、一组对边平行另一组对边相等的四边形可以是等腰梯形,可以是平行四边形,故选项A不合题意;
B、对角线互相垂直平分的四边形是菱形,故选项B符合题意;
C、对角线相等的平行四边形是矩形,故选项C不合题意;
D、对角线互相垂直平分且相等的四边形是正方形,故选项D不合题意;
故选:B.
5.解:如图,
因为以正方形的边长为直径,在正方形内画半圆得到的图形,
所以此图形的对称轴有4条.
故选:B.
6.解:∵ABCD是正方形,
∴∠ABF=∠C=90°,AB=BC,
∵BF=CE,
∴△ABF≌△BCE(SAS),
∴AF=BE(A正确),∠BAF=∠CBE,∠AFB=∠BEC(B错误),
∵∠BAF+∠DAF=90°,∠ABE+∠EBC=90°,
∴∠DAF=∠ABE(C正确),
∵∠BAF=∠CBE,∠BAF+∠AFB=90°,
∴∠CBE+∠AFB=90°,
∴AG⊥BE(第四个正确),
所以不正确的是B,
故选:B.
7.解:∵四边形OBCD是正方形,
∴OB=BC=CD=OD,∠CDO=∠CBO=90°,
∵O,D两点的坐标分别是(0,0),(0,6),
∴OD=6,
∴OB=BC=CD=6,
∴C(6,6).
故选:D.
8.解:A、根据平行四边形的性质得到OA=OC,OB=OD,该结论正确;
B、当AB=CD时,四边形ABCD还是平行四边形,该选项错误;
C、根据有一个角是直角的平行四边形是矩形可以判断该选项正确;
D、当AC=BD且AC⊥BD时,根据对角线相等可判断四边形ABCD是矩形,根据对角线互相垂直可判断四边形ABCD 是菱形,故四边形ABCD是正方形,该结论正确;
故选:B.
9.解:设直线AB的解析式为y=kx+b,
∵顶点A,B的坐标分别为(﹣2,6)和(7,0).
∴,
∴,
∴,
∵∠ACB=90°,边BC在x轴上,∴C点的坐标为(﹣2,0),
∴正方形OCDE的边长为2,
∴E(0,2),设点E沿x轴平移后落在AB边上的坐标为(a,2),
由y=﹣得,2=﹣a+,
∴a=4,
∴当点E落在AB边上时,点D的坐标为(2,2),
故选:B.
10.解:对角线相等的四边形推不出是正方形或矩形,
故①→②,①→③错误,
故选项B,C,D错误,
故选:A.
11.解:以O为原点,垂直AB的直线为x轴,建立直角坐标系,如图:
∵正方形ABCD的边长为4,CE=2,DF=1,
∴E(4,﹣2),F(2,3),
∵G为EF的中点,
∴G(3,),
设直线OE解析式为y=kx,将E(4,﹣2)代入得:
﹣2=4k,解得k=﹣,
∴直线OE解析式为y=﹣x,
令x=2得y=﹣1,
∴H(2,﹣1),
∴GH==,
方法二:如下图,连接OF,过点O作OM⊥CD交CD于M,
∵O为正方形对角线AC和BD的交点,
∴OM=CM=DM=CE=2,易证△OHM≌△EHC,
∴点H、点G分别为OE、FE的中点,
∴GH为△OEF的中位线,
∴GH=OF,
在Rt△OMF中,由勾股定理可得OF===,
∴GH=OF=,
故答案为:.
12.解:①当B为直角顶点时,过D作DH⊥AB于H,如图:
∵△ABC的三个顶点都是同一个正方形的顶点,∠ABC的平分线与线段AC交于点D,
∴△ABC是等腰直角三角形,∠ABD=∠ADH=45°,AD=CD=AC,
∴△AHD和△BHD是等腰直角三角形,
∴AH=DH=BH,
∴DH=BC,
若AC=6,则BC=3,此时DH=,即点D到直线AB的距离为;
若AB=BC=6,则DH=BC=3,即点D到直线AB的距离为3;
②当B不是直角顶点时,过D作DH⊥BC于H,如图:
∵△ABC的三个顶点都是同一个正方形的顶点,∠ABC的平分线与线段AC交于点D,
∴△CDH是等腰直角三角,AD=DH=CH,
在△ABD和△HBD中,
,
∴△ABD≌△HBD(AAS),
∴AB=BH,
若AB=AC=6时,BH=6,BC==6,
∴CH=BC﹣BH=6﹣6,
∴AD=6﹣6,即此时点D到直线AB的距离为6﹣6;
若BC=6,则AB=3,
∴BH=3,
∴CH=6﹣3,
∴AD=6﹣3,即此时点D到直线AB的距离为6﹣3;
综上所述,点D到直线AB的距离为或3或6﹣6或6﹣3.
故答案为:或3或6﹣6或6﹣3.
13.解:∵四边形ABCD是正方形,
∴AB=BC=CD=AD,∠B=∠BCD=∠D=∠BAD=90°,
∵△AEF等边三角形,
∴AE=EF=AF,∠EAF=60°,
∴∠BAE+∠DAF=30°,
在Rt△ABE和Rt△ADF中,
,
∴Rt△ABE≌Rt△ADF(HL),
∴BE=DF,∠BAE=∠DAF,
故①正确;
∵∠BAE+∠DAF=30°,
∴∠DAF+∠DAF=30°,
即∠DAF=15°,
故②正确;
∵BC=CD,
∴BC﹣BE=CD﹣DF,即CE=CF,
∵Rt△ABE≌Rt△ADF,
∴AE=AF,
∴AC垂直平分EF,
∴EG=FG,
故③正确;
∵∠ECF=90°,EG=FG,
∴CG=EF,
设EC=FC=x,由勾股定理,得EF==x,
∴CG=EF=x=CE,
故④正确;
综上所述,正确的有①②③④,共4个
14.解:由题意可得,
直角三角形的斜边长为3,一条直角边长为2,
故直角三角形的另一条直角边长为:=,
故阴影部分的面积是:=4,
故答案为:4.
15.解:如图,连接AC,BD交于点H,过点O和点H的直线MN平分该组合图形的面积,交AD于S,取AE中点P,取AB中点Q,连接OP,HQ,过点O作OT⊥QH于T,
∵四边形ABCD是矩形,
∴AH=HC,
又∵Q是AB中点,
∴QH=BC=4,QH∥BC,AQ=BQ=2,
同理可求PO=AG=2,PO∥AG,EP=AP=2,
∴PO∥AD∥BC∥EF∥QH,EP=AP=AQ=BQ,
∴MO=OS=SH=NH,∠OPQ=∠PQH=90°,
∵OT⊥QH,
∴四边形POTQ是矩形,
∴PO=QT=2,OT=PQ=4,
∴TH=2,
∴OH===2,
∴MN=2OH=4,
故答案为:4.
16.解:如图,连接DH,HM.
由题可得,AM=BE,
∴AB=EM=AD,
∵四边形ABCD是正方形,EH⊥AC,
∴EM=AD,∠AHE=90°,∠MEH=∠DAH=45°=∠EAH,
∴EH=AH,
∴△MEH≌△DAH(SAS),
∴∠MHE=∠DHA,MH=DH,
∴∠MHD=∠AHE=90°,△DHM是等腰直角三角形,
∴DM=HM,故②正确;
当∠DHC=60°时,∠ADH=60°﹣45°=15°,
∴∠ADM=45°﹣15°=30°,
∴Rt△ADM中,DM=2AM,
即DM=2BE,故①正确;
∵CD∥EM,EC∥DM,
∴四边形CEMD是平行四边形,
∵DM>AD,AD=CD,
∴DM>CD,
∴四边形CEMD不可能是菱形,故③错误,
∵点M是边BA延长线上的动点(不与点A重合),且AM<AB,
∴∠AHM<∠BAC=45°,
∴∠CHM>135°,故④正确;
由上可得正确结论的序号为①②④.
故答案为①②④.
17.解:∵四边形ABCD是正方形,
∴∠ACB=∠BAC=45°,
∴∠2+∠BCP=45°,
∵∠1=∠2,
∴∠1+∠BCP=45°,
∵∠BPC=180°﹣∠1﹣∠BCP,
∴∠BPC=135°,
故答案为:135.
18.解:∵正方形ABCD中,∠BAD=∠ADF=90°,∠BAE=56°,
∴∠DAF=34°,∠DFE=56°,
∵AD=CD,∠ADE=∠CDE,DE=DE,
∴△ADE≌△CDE(SAS),
∴∠DCE=∠DAF=34°,
∵∠DFE是△CEF的外角,
∴∠CEF=∠DFE﹣∠DCE=56°﹣34°=22°,
故答案为:22.
19.解;(1)证明:由正方形对角线平分每一组对角可知:∠DAE=∠BCF=45°,
在△ADE和△CBF中,
,
∴△ADE≌△CBF(SAS).
(2)∵AB=AD=,
∴BD===8,
由正方形对角线相等且互相垂直平分可得:AC=BD=8,DO=BO=4,OA=OC=4,
又AE=CF=2,
∴OA﹣AE=OC﹣CF,
即OE=OF=4﹣2=2,
故四边形BEDF为菱形.
∵∠DOE=90°,
∴DE===2.
∴4DE=
故四边形BEDF的周长为8.
20.证明:∵四边形ABCD为正方形,
∴OD=OC,∠ODF=∠OCE=45°,∠COD=90°,
∴∠DOF+∠COF=90°,
∵∠EOF=90°,即∠COE+∠COF=90°,
∴∠COE=∠DOF,
∴△COE≌△DOF(ASA),
∴CE=DF.
21.解:(1)证明:∵四边形ABCD是正方形,
∴AB=AD,∠BAF+∠DAE=90°,
∵DE⊥AG,
∴∠DAE+∠ADE=90°,
∴∠ADE=∠BAF,
又∵BF∥DE,
∴∠BFA=90°=∠AED,
∴△ABF≌△DAE(AAS),
∴AE=BF,
∴AF﹣BF=AF﹣AE=EF;
(2)不可能,理由是:
如图,若要四边形BFDE是平行四边形,
已知DE∥BF,则当DE=BF时,四边形BFDE为平行四边形,
∵DE=AF,
∴BF=AF,即此时∠BAF=45°,
而点G不与B和C重合,
∴∠BAF≠45°,矛盾,
∴四边形BFDE不可能是平行四边形.
22.解:证明:在正方形ABCD中,
AB=BC=CD=DA,∠ABE=∠BCF=90°,
∵CE=DF,
∴BE=CF,
在△AEB与△BFC中,
,
∴△AEB≌△BFC(SAS),
∴AE=BF.
23.证明:∵四边形ABCD,四边形ECGF都是正方形
∴DA∥BC,AD=CD,FG=CG,∠B=∠CGF=90°
∵AD∥BC,AH∥DG
∴四边形AHGD是平行四边形
∴AH=DG,AD=HG=CD
∵CD=HG,∠ECG=∠CGF=90°,FG=CG
∴△DCG≌△HGF(SAS)
∴DG=HF,∠HFG=∠HGD
∴AH=HF,
∵∠HGD+∠DGF=90°
∴∠HFG+∠DGF=90°
∴DG⊥HF,且AH∥DG
∴AH⊥HF,且AH=HF
∴△AHF为等腰直角三角形.
24.(1)证明:∵四边形ABCD是正方形,
∴AB=AD,∠ABC=∠ADC=∠ADF=90°,
在△ABE和△ADF中,
,
∴△ABE≌△ADF(SAS);
(2)解:∵△ABE≌△ADF,
∴AE=AF,∠BAE=∠DAF,
∵∠BAE+∠EAD=90°,
∴∠DAF+∠EAD=90°,即∠EAF=90°,
∴EF=AE=5.
25.证明:(1)∵四边形ABCD是正方形,
∴AB=BC,∠ABC=∠BCD=90°,
∴∠ABE=∠BCF=90°,
在△ABE和△BCF中,,
∴△ABE≌△BCF(SAS),
∴AE=BF,∠BAE=∠CBF,
∵EG∥BF,
∴∠CBF=∠CEG,
∵∠BAE+∠BEA=90°,
∴∠CEG+∠BEA=90°,
∴AE⊥EG,
∴AE⊥BF;
(2)延长AB至点P,使BP=BE,连接EP,如图所示:
则AP=CE,∠EBP=90°,
∴∠P=45°,
∵CG为正方形ABCD外角的平分线,
∴∠ECG=45°,
∴∠P=∠ECG,
由(1)得∠BAE=∠CEG,
在△APE和△ECG中,,
∴△APE≌△ECG(ASA),
∴AE=EG,
∵AE=BF,
∴EG=BF,
∵EG∥BF,
∴四边形BEGF是平行四边形.
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
