2021-2022学年暑假自主学习苏科版九年级数学上册1.4用一元二次方程解决问题培优提升训练(word解析版)
文档属性
| 名称 | 2021-2022学年暑假自主学习苏科版九年级数学上册1.4用一元二次方程解决问题培优提升训练(word解析版) |  | |
| 格式 | doc | ||
| 文件大小 | 444.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-08 07:59:04 | ||
图片预览




文档简介
2021年苏科版九年级数学上册《1.4用一元二次方程解决问题》暑假自主学习
培优提升训练(附答案)
1.一个两位数比它的十位上的数字与个位上的数字之积大,已知十位上的数字比个位上的数字大.则这个两位数是( )
A.64 B.75 C.53或75 D.64或75
2.已知方程x2+bx+c=0有两个相等的实数根,且当x=a与x=a+n时,x2+bx+c=m,则m、n的关系为( )
A.m=n B.m=n C.m=n2 D.m=n2
3.一个矩形内放入两个边长分别为3cm和4cm的小正方形纸片,按照图①放置,矩形纸片没有被两个正方形纸片覆盖的部分(黑色阴影部分)的面积为8cm2;按照图②放置,矩形纸片没有被两个正方形纸片覆盖的部分的面积为11cm2,若把两张正方形纸片按图③放置时,矩形纸片没有被两个正方形纸片覆盖的部分的面积为( )
A.6cm2 B.7 cm2 C.12cm2 D.19 cm2
4.一个容器盛满纯药液千克,第一次倒出一部分药液后加满水,第二次又倒出同样多的药液,再加满水,此时容器内的纯药液利下千克,那么每次倒出的药液是( )
A.千克 B.千克 C.千克 D.千克
5.某商场将进货价为45元的某种服装以65元售出,平均每天可售30件,为了尽快减少库存,商场决定采取适当的降价措施,调查发现:每件降价1元,则每天可多售5件,如果每天要盈利800元,每件应降价( )
A.12元 B.10元 C.11元 D.9元
6.某钢铁厂一月份生产钢铁560吨,从二月份起,由于改进操作技术,使得第一季度共生产钢铁1850吨,问二、三月份平均每月的增长率是多少?若设二、三月份平均每月的增长率为x,则可得方程( )
A. B.
C. D.
7.我区某校举行冬季运动会,其中一个项目是乒乓球比赛,比赛为单循环制,即所有参赛选手彼此恰好比赛一场. 记分规则是:每场比赛胜者得3分、负者得0分、平局各得1分. 赛后统计,所有参赛者的得分总知为210分,且平局数不超过比赛总场数的,本次友谊赛共有参赛选手__________人.
8.已知点,在双曲线上,且满足,.若,则__________.
9.某商场销售一批名牌衬衫,平均每天可售出20件,每件可 盈利40元.为了扩大销售量,增加盈利,采取了降价措施,经调查发现如果每件计划降价1元,那么商场平均每天可多售出2件.若商场平均每天要赢利1200元,则每件衬衫应降价________.
10.在中,,厘米,厘米,点P从点A开始沿AB边向B点以1厘米/秒的速度移动,点Q从点B开始沿BC边向点C以2厘米/秒的速度移动,如果点P,Q分别从A,B两点同时出发,则经过______秒后,P,Q两点间距离为厘米.
11.在正方形ABCD中,点E在直线AB上,EF⊥AC于点F,连接EC,EC=5,△EFC的周长为12,则AE的长为______.
12.准备在一块长为30米,宽为24米的长方形花圃内修建四条宽度相等,且与各边垂直的小路,(如图所示)四条小路围成的中间部分恰好是一个正方形,且边长是小路宽度的4倍,若四条小路所占面积为80平方米,则小路的宽度为_____米.
13.如图,一块矩形铁皮的长是宽的2倍,将这个铁皮的四角各剪去一个边长为3cm的小正方形,做成一个无盖的盒子,若盒子的容积是240cm3,则原铁皮的宽为______cm.
14.第五届中国机器人峰会将于5月9日在余姚开幕,某公司购买一种T恤衫参加此次峰会.了解到某商店正好有这种T恤衫的促销,当购买10件时每件140元,购买数量每增加1件单价减少1元;当购买数量为60件(含60件)以上时,一律每件80元.
(1)如果购买件(10<<60),每件的单价为元,请写出关于的函数关系式;
(2)如果该公司共购买了100件T恤衫,由于某种原因需分两批购买,且第一批购买量多于30件且少于60件.已知购买两批T恤衫一共花了9200元,求第一批T恤衫的购买数量.
15.为了倡导节能低碳的生活,某公司对集体宿舍用电收费作如下规定:一间宿舍一个月用电量不超过a千瓦时,则一个月的电费为20元;若超过a千瓦时,则除了交20元外,超过部分每千瓦时要交元。某宿舍3月份用电80千瓦时,交电费35元;4月份用电45千瓦时,交电费20元。
(1)求a的值;
(2)若该宿舍5月份交电费45元,那么该宿舍当月用电量为多少千瓦时?
16.如图,A、B、C、D为矩形的4个顶点,AB=16cm,BC=6cm,动点P、Q分别以3cm/s、2cm/s的速度从点A、C同时出发,点Q从点C向点D移动.
(1)若点P从点A移动到点B停止,点P、Q分别从点A、C同时出发,问经过2s时P、Q两点之间的距离是多少cm?
(2)若点P从点A移动到点B停止,点Q随点P的停止而停止移动,点P、Q分别从点A、C同时出发,问经过多长时间P、Q两点之间的距离是10cm?
(3)若点P沿着AB→BC→CD移动,点P、Q分别从点A、C同时出发,点Q从点C移动到点D停止时,点P随点Q的停止而停止移动,试探求经过多长时间△PBQ的面积为12cm2?
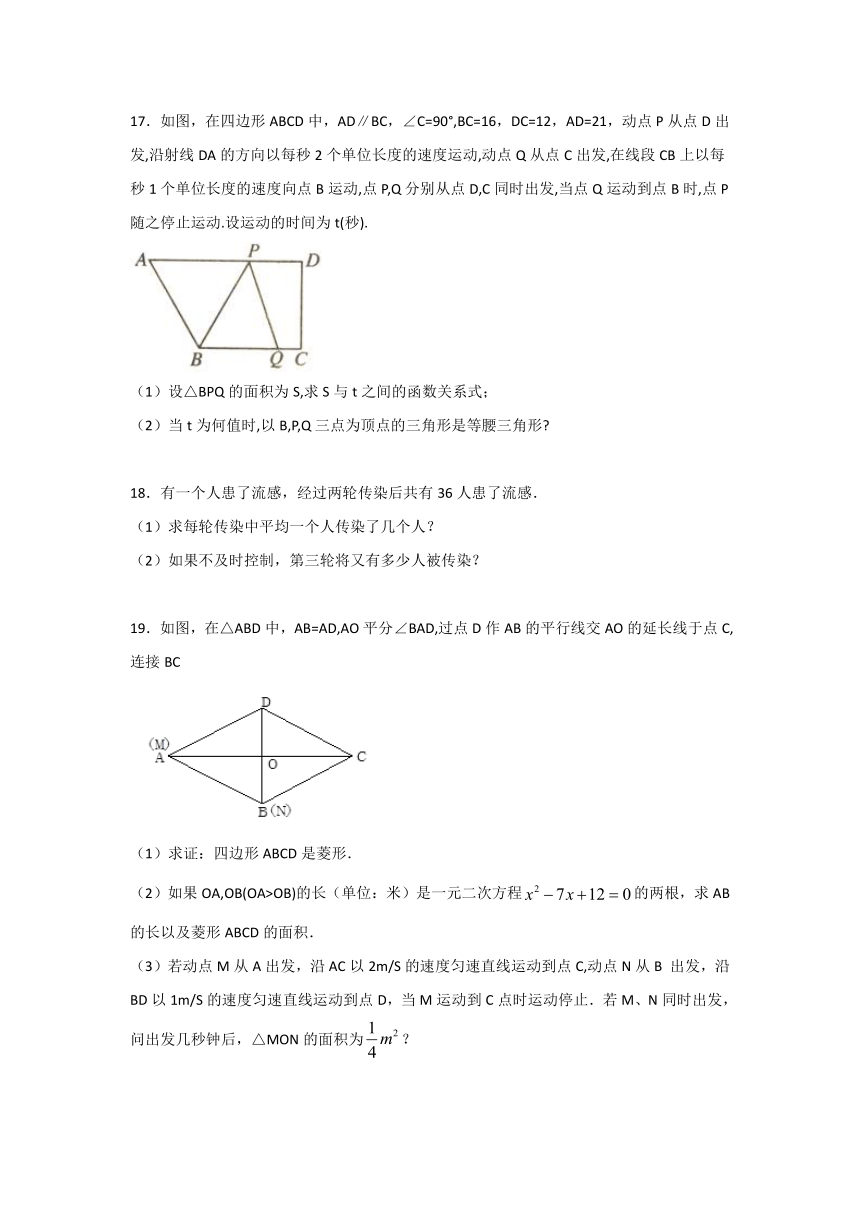
17.如图,在四边形ABCD中,AD∥BC,∠C=90°,BC=16,DC=12,AD=21,动点P从点D出发,沿射线DA的方向以每秒2个单位长度的速度运动,动点Q从点C出发,在线段CB上以每秒1个单位长度的速度向点B运动,点P,Q分别从点D,C同时出发,当点Q运动到点B时,点P随之停止运动.设运动的时间为t(秒).
(1)设△BPQ的面积为S,求S与t之间的函数关系式;
(2)当t为何值时,以B,P,Q三点为顶点的三角形是等腰三角形?
18.有一个人患了流感,经过两轮传染后共有36人患了流感.
(1)求每轮传染中平均一个人传染了几个人?
(2)如果不及时控制,第三轮将又有多少人被传染?
19.如图,在△ABD中,AB=AD,AO平分∠BAD,过点D作AB的平行线交AO的延长线于点C,连接BC
(1)求证:四边形ABCD是菱形.
(2)如果OA,OB(OA>OB)的长(单位:米)是一元二次方程的两根,求AB的长以及菱形ABCD的面积.
(3)若动点M从A出发,沿AC以2m/S的速度匀速直线运动到点C,动点N从B 出发,沿BD以1m/S的速度匀速直线运动到点D,当M运动到C点时运动停止.若M、N同时出发,问出发几秒钟后,△MON的面积为?
20.电子信息产业是重庆市的重要支柱产业,根据2019年的统计数据,全国每10台手机就有一台产自重庆,全球每10台电脑就有4台产自重庆,二娃手机连锁店顺应时代趋势,今年主打炫酷版摄影手机和实用版抗摔手机,售价各为6600元和3000元,在9月底共售出1200部,总销售额为6120000元.
(1)二娃手机厂9月销售炫酷版手机多少部?
(2)由于销售状况良好,二娃准备10月扩大销售规模,需要将炫酷版价格下调600元,实用版价格降低,预估炫酯版销售量会增加,实用版销售量会增加,预计销售额将会比9月少120000元,则m的值为多少?
参考答案
1 2 3 4 5 6
D D B B B D
7.13
解:设所有比赛中分出胜负的有x场,平局y场,得:
由①得:2y=210-3x
由②得:2y≤x
∴210-3x≤x
解得:x≥,
∵x、y均为非负整数
∴,,,……,
设参赛选手有a人,得:=x+y
化简得:a2-a-2(x+y)=0
∵此关于a的一元二次方程有正整数解
∴△=1+8(x+y)必须为平方数
由得:1+8×(54+24)=625,为25的平方
∴解得:a1=-12(舍去),a2=13
∴共参赛选手有13人.
故答案为:13.
8.
解:根据题意可知:是双曲线与一次函数的两个交点,联立方程消去得,
由韦达定理得,
故答案为:
9.10元或20元
解:设商场平均每天要赢利1200元,每件衬衫应降价x元,(40﹣x)(20+2x)=1200,解得x1=10,x2=20,即商场平均每天要赢利1200元,每件衬衫应降价10元或20元.
故答案为:10元或20元.
10.
解:设经过秒后,P,Q两点间距离为厘米,
由题意得:点P从点A开始沿AB边运动到点B所需时间为秒,
点Q从点B开始沿BC边运动到点C所需时间为秒,
因此,分以下三种情况:
(1)当点Q到达点C之前,即时,则厘米,厘米,
厘米,
厘米,
则在中,,即,
整理得:,
解得或(不符题设,舍去);
(2)当点Q到达点C,点P继续向点B移动,即时,则厘米,
由得:,
整理得:,
解得或(均不符题设,舍去);
(3)当点Q到达点C,点P到达点B,即时,
则厘米,不符题意;
综上,经过秒后,P,Q两点间距离为厘米,
故答案为:.
11.
解:∵ABCD是正方形,∴∠BAC=45°.∵EF⊥AC,∴AF=EF.设AF=x,则EF=x,FC=12-5-x=7-x.在Rt△EFC中,∵EF2+FC2=EC2,∴x2+(7-x)2=52,整理得:x2-7x+12=0,解得:x=3或x=4,∴AE=AF=x=或.故答案为或.
12.1.25
解:设小路的宽度为,由题意和图示可知,小路的面积为
,解一元二次方程,由,可得.
13.11.
解:设这块铁片的宽为xcm,则铁片的长为2xcm,由题意,得3(2x﹣6)(x﹣6)=240,解得x1=11,x2=﹣2(不合题意,舍去),答:这块铁片的宽为11cm.
故答案为11.
14.(1)y=150-x;(2)40件
解:(1)购买x件(10<x<60)时,y=140-(x-10)=150-x.
故y关于x的函数关系式是y=150-x;
(2)设第一批购买x件,则第二批购买(100-x)件.
①当30<x≤40时,则60≤100-x<100,则x(150-x)+80(100-x)=9200,
解得=30(舍去),=40;
②当40<x<60时,则40<100-x<60,
则x(150-x)+(100-x) [150-(100-x)]=9200,
解得x=30或x=70,但40<x<60,所以无解;
答:第一批购买数量为40件..
15.(1)50(2)若该宿舍5月份交电费45元,那么该宿舍当月用电量为100千瓦时。
解:(1)根据3月份用电80千瓦时,交电费35元,得,
,即。
解得a=30或a=50。
由4月份用电45千瓦时,交电费20元,得,a≥45。
∴a=50。
(2)设月用电量为x千瓦时,交电费y元。则
∵5月份交电费45元,∴5月份用电量超过50千瓦时。
∴45=20+0.5(x-50),解得x=100。
(1)根据3月份用电80千瓦时,交电费35元列出方程求解,结合4月份用电45千瓦时,交电费20元,确定a的范围,从而得出结果。
(2)列出电费y元与用电量x千瓦时的函数关系式,根据5月份交电费45元,代入即可。
16.(1)PQ=6cm;(2)s或s;(3)经过4秒或6秒△PBQ的面积为 12cm2.
解:(1)过点P作PE⊥CD于E.
则根据题意,得
EQ=16-2×3-2×2=6(cm),PE=AD=6cm;
在Rt△PEQ中,根据勾股定理,得
PE2+EQ2=PQ2,即36+36=PQ2,
∴PQ=6cm;
∴经过2s时P、Q两点之间的距离是6cm;
(2)设x秒后,点P和点Q的距离是10cm.
(16-2x-3x)2+62=102,即(16-5x)2=64,
∴16-5x=±8,
∴x1=,x2=;
∴经过s或sP、Q两点之间的距离是10cm;
(3)连接BQ.设经过ys后△PBQ的面积为12cm2.
①当0≤y≤时,则PB=16-3y,
∴PB?BC=12,即×(16-3y)×6=12,
解得y=4;
②当<x≤时,
BP=3y-AB=3y-16,QC=2y,则
BP?CQ=(3y-16)×2y=12,
解得y1=6,y2=-(舍去);
③<x≤8时,
QP=CQ-PQ=22-y,则
QP?CB=(22-y)×6=12,
解得y=18(舍去).
综上所述,经过4秒或6秒△PBQ的面积为 12cm2.
考点:一元二次方程的应用.
17.(1)s=96﹣6t (2)或
解:(1)过点P作PM⊥BC于M,则四边形PDCM为矩形.
∴PM=DC=12,
∵QB=16﹣t,
∴S=QB?PM=(16﹣t)×12=96﹣6t
(2)由图可知,CM=PD=2t,CQ=t,若以B、P、Q为顶点的三角形是等腰三角形,可以分三种情况:
①若PQ=BQ,在Rt△PMQ中,PQ2=t2+122,
由PQ2=BQ2得t2+122=(16﹣t)2,解得t=;
②若BP=BQ,在Rt△PMB中,PB2=(16﹣2t)2+122,由PB2=BQ2得(16﹣2t)2+122=(16﹣t)2,即3t2﹣32t+144=0,
此时,△=(﹣32)2﹣4×3×144=﹣704<0,所以此方程无解,
∴BP≠BQ.
③若PB=PQ,由PB2=PQ2得t2+122=(16﹣2t)2+122得t1=,t2=16(不合题意,舍去).
综上所述,当t=或t=时,以B,P,Q三点为顶点的三角形是等腰三角形.
18.(1)5;(2)180
解:(1)设每轮传染中平均一个人传染了x个人,根据题意得:
x+1+(x+1)x=36,
解得:x=5或x=﹣7(舍去).
答:每轮传染中平均一个人传染了5个人;
(2)根据题意得:5×36=180(个),
答:第三轮将又有180人被传染.
19.(1)证明;(2)5,24;(3)M,N出发秒,秒,秒钟后,△MON的面积为m2.
解:(1)证明:∵AO平分∠BAD,AB∥CD
∴∠DAC=∠BAC=∠DCA
∴△ACD是等腰三角形,AD=DC
又∵AB=AD
∴AB=CD,
∴四边形ABCD为平行四边形,
又∵AB=AD,∴?ABCD是菱形;
(2)解:解方程x2-7x+12=0,得
OA=4,OB=3,
利用勾股定理AB==5,
S菱形ABCD=AC×BD=×8×6=24平方米.
(3)解:在第(2)问的条件下,设M、N同时出发x秒钟后,△MON的面积为m2,
当点M在OA上时,x≤2,S△MON=(4-2x)(3-x)=;
解得x1=,x2=(大于2,舍去);
当点M在OC上且点N在OB上时,2<x<3,S△MON=(3-x)(2x-4)=,
解得x1=x2=;
当点M在OC上且点N在OD上时,即3≤x≤4,S△MON=(2x-4)(x-3)=;
解得x1=,x2=(小于3,舍去).
综上所述:M,N出发秒,秒,秒钟后,△MON的面积为m2.
20.(1)700;(2)10.
解:(1)二娃手机厂9月销售炫酷版手机x部,则实用版抗摔手机(1200-x)部
根据题意得:6600x+3000(1200-x)=6120000
解得x=700.
答:二娃手机厂9月销售炫酷版手机700部;
(2)由题意得:炫酷版摄影手机和实用版抗摔手机10月份的价格分别为:6600-600=6000元,3000(1-m%)元;预估销售量分别为:700(1+),500(1+);
则根据题意得:
6000×700(1+)+3000(1-m%)500(1+)+120000=6120000
化简得:m2-110m+1000=0,解得:m=10或m=100(舍).
答:的值为10.
培优提升训练(附答案)
1.一个两位数比它的十位上的数字与个位上的数字之积大,已知十位上的数字比个位上的数字大.则这个两位数是( )
A.64 B.75 C.53或75 D.64或75
2.已知方程x2+bx+c=0有两个相等的实数根,且当x=a与x=a+n时,x2+bx+c=m,则m、n的关系为( )
A.m=n B.m=n C.m=n2 D.m=n2
3.一个矩形内放入两个边长分别为3cm和4cm的小正方形纸片,按照图①放置,矩形纸片没有被两个正方形纸片覆盖的部分(黑色阴影部分)的面积为8cm2;按照图②放置,矩形纸片没有被两个正方形纸片覆盖的部分的面积为11cm2,若把两张正方形纸片按图③放置时,矩形纸片没有被两个正方形纸片覆盖的部分的面积为( )
A.6cm2 B.7 cm2 C.12cm2 D.19 cm2
4.一个容器盛满纯药液千克,第一次倒出一部分药液后加满水,第二次又倒出同样多的药液,再加满水,此时容器内的纯药液利下千克,那么每次倒出的药液是( )
A.千克 B.千克 C.千克 D.千克
5.某商场将进货价为45元的某种服装以65元售出,平均每天可售30件,为了尽快减少库存,商场决定采取适当的降价措施,调查发现:每件降价1元,则每天可多售5件,如果每天要盈利800元,每件应降价( )
A.12元 B.10元 C.11元 D.9元
6.某钢铁厂一月份生产钢铁560吨,从二月份起,由于改进操作技术,使得第一季度共生产钢铁1850吨,问二、三月份平均每月的增长率是多少?若设二、三月份平均每月的增长率为x,则可得方程( )
A. B.
C. D.
7.我区某校举行冬季运动会,其中一个项目是乒乓球比赛,比赛为单循环制,即所有参赛选手彼此恰好比赛一场. 记分规则是:每场比赛胜者得3分、负者得0分、平局各得1分. 赛后统计,所有参赛者的得分总知为210分,且平局数不超过比赛总场数的,本次友谊赛共有参赛选手__________人.
8.已知点,在双曲线上,且满足,.若,则__________.
9.某商场销售一批名牌衬衫,平均每天可售出20件,每件可 盈利40元.为了扩大销售量,增加盈利,采取了降价措施,经调查发现如果每件计划降价1元,那么商场平均每天可多售出2件.若商场平均每天要赢利1200元,则每件衬衫应降价________.
10.在中,,厘米,厘米,点P从点A开始沿AB边向B点以1厘米/秒的速度移动,点Q从点B开始沿BC边向点C以2厘米/秒的速度移动,如果点P,Q分别从A,B两点同时出发,则经过______秒后,P,Q两点间距离为厘米.
11.在正方形ABCD中,点E在直线AB上,EF⊥AC于点F,连接EC,EC=5,△EFC的周长为12,则AE的长为______.
12.准备在一块长为30米,宽为24米的长方形花圃内修建四条宽度相等,且与各边垂直的小路,(如图所示)四条小路围成的中间部分恰好是一个正方形,且边长是小路宽度的4倍,若四条小路所占面积为80平方米,则小路的宽度为_____米.
13.如图,一块矩形铁皮的长是宽的2倍,将这个铁皮的四角各剪去一个边长为3cm的小正方形,做成一个无盖的盒子,若盒子的容积是240cm3,则原铁皮的宽为______cm.
14.第五届中国机器人峰会将于5月9日在余姚开幕,某公司购买一种T恤衫参加此次峰会.了解到某商店正好有这种T恤衫的促销,当购买10件时每件140元,购买数量每增加1件单价减少1元;当购买数量为60件(含60件)以上时,一律每件80元.
(1)如果购买件(10<<60),每件的单价为元,请写出关于的函数关系式;
(2)如果该公司共购买了100件T恤衫,由于某种原因需分两批购买,且第一批购买量多于30件且少于60件.已知购买两批T恤衫一共花了9200元,求第一批T恤衫的购买数量.
15.为了倡导节能低碳的生活,某公司对集体宿舍用电收费作如下规定:一间宿舍一个月用电量不超过a千瓦时,则一个月的电费为20元;若超过a千瓦时,则除了交20元外,超过部分每千瓦时要交元。某宿舍3月份用电80千瓦时,交电费35元;4月份用电45千瓦时,交电费20元。
(1)求a的值;
(2)若该宿舍5月份交电费45元,那么该宿舍当月用电量为多少千瓦时?
16.如图,A、B、C、D为矩形的4个顶点,AB=16cm,BC=6cm,动点P、Q分别以3cm/s、2cm/s的速度从点A、C同时出发,点Q从点C向点D移动.
(1)若点P从点A移动到点B停止,点P、Q分别从点A、C同时出发,问经过2s时P、Q两点之间的距离是多少cm?
(2)若点P从点A移动到点B停止,点Q随点P的停止而停止移动,点P、Q分别从点A、C同时出发,问经过多长时间P、Q两点之间的距离是10cm?
(3)若点P沿着AB→BC→CD移动,点P、Q分别从点A、C同时出发,点Q从点C移动到点D停止时,点P随点Q的停止而停止移动,试探求经过多长时间△PBQ的面积为12cm2?
17.如图,在四边形ABCD中,AD∥BC,∠C=90°,BC=16,DC=12,AD=21,动点P从点D出发,沿射线DA的方向以每秒2个单位长度的速度运动,动点Q从点C出发,在线段CB上以每秒1个单位长度的速度向点B运动,点P,Q分别从点D,C同时出发,当点Q运动到点B时,点P随之停止运动.设运动的时间为t(秒).
(1)设△BPQ的面积为S,求S与t之间的函数关系式;
(2)当t为何值时,以B,P,Q三点为顶点的三角形是等腰三角形?
18.有一个人患了流感,经过两轮传染后共有36人患了流感.
(1)求每轮传染中平均一个人传染了几个人?
(2)如果不及时控制,第三轮将又有多少人被传染?
19.如图,在△ABD中,AB=AD,AO平分∠BAD,过点D作AB的平行线交AO的延长线于点C,连接BC
(1)求证:四边形ABCD是菱形.
(2)如果OA,OB(OA>OB)的长(单位:米)是一元二次方程的两根,求AB的长以及菱形ABCD的面积.
(3)若动点M从A出发,沿AC以2m/S的速度匀速直线运动到点C,动点N从B 出发,沿BD以1m/S的速度匀速直线运动到点D,当M运动到C点时运动停止.若M、N同时出发,问出发几秒钟后,△MON的面积为?
20.电子信息产业是重庆市的重要支柱产业,根据2019年的统计数据,全国每10台手机就有一台产自重庆,全球每10台电脑就有4台产自重庆,二娃手机连锁店顺应时代趋势,今年主打炫酷版摄影手机和实用版抗摔手机,售价各为6600元和3000元,在9月底共售出1200部,总销售额为6120000元.
(1)二娃手机厂9月销售炫酷版手机多少部?
(2)由于销售状况良好,二娃准备10月扩大销售规模,需要将炫酷版价格下调600元,实用版价格降低,预估炫酯版销售量会增加,实用版销售量会增加,预计销售额将会比9月少120000元,则m的值为多少?
参考答案
1 2 3 4 5 6
D D B B B D
7.13
解:设所有比赛中分出胜负的有x场,平局y场,得:
由①得:2y=210-3x
由②得:2y≤x
∴210-3x≤x
解得:x≥,
∵x、y均为非负整数
∴,,,……,
设参赛选手有a人,得:=x+y
化简得:a2-a-2(x+y)=0
∵此关于a的一元二次方程有正整数解
∴△=1+8(x+y)必须为平方数
由得:1+8×(54+24)=625,为25的平方
∴解得:a1=-12(舍去),a2=13
∴共参赛选手有13人.
故答案为:13.
8.
解:根据题意可知:是双曲线与一次函数的两个交点,联立方程消去得,
由韦达定理得,
故答案为:
9.10元或20元
解:设商场平均每天要赢利1200元,每件衬衫应降价x元,(40﹣x)(20+2x)=1200,解得x1=10,x2=20,即商场平均每天要赢利1200元,每件衬衫应降价10元或20元.
故答案为:10元或20元.
10.
解:设经过秒后,P,Q两点间距离为厘米,
由题意得:点P从点A开始沿AB边运动到点B所需时间为秒,
点Q从点B开始沿BC边运动到点C所需时间为秒,
因此,分以下三种情况:
(1)当点Q到达点C之前,即时,则厘米,厘米,
厘米,
厘米,
则在中,,即,
整理得:,
解得或(不符题设,舍去);
(2)当点Q到达点C,点P继续向点B移动,即时,则厘米,
由得:,
整理得:,
解得或(均不符题设,舍去);
(3)当点Q到达点C,点P到达点B,即时,
则厘米,不符题意;
综上,经过秒后,P,Q两点间距离为厘米,
故答案为:.
11.
解:∵ABCD是正方形,∴∠BAC=45°.∵EF⊥AC,∴AF=EF.设AF=x,则EF=x,FC=12-5-x=7-x.在Rt△EFC中,∵EF2+FC2=EC2,∴x2+(7-x)2=52,整理得:x2-7x+12=0,解得:x=3或x=4,∴AE=AF=x=或.故答案为或.
12.1.25
解:设小路的宽度为,由题意和图示可知,小路的面积为
,解一元二次方程,由,可得.
13.11.
解:设这块铁片的宽为xcm,则铁片的长为2xcm,由题意,得3(2x﹣6)(x﹣6)=240,解得x1=11,x2=﹣2(不合题意,舍去),答:这块铁片的宽为11cm.
故答案为11.
14.(1)y=150-x;(2)40件
解:(1)购买x件(10<x<60)时,y=140-(x-10)=150-x.
故y关于x的函数关系式是y=150-x;
(2)设第一批购买x件,则第二批购买(100-x)件.
①当30<x≤40时,则60≤100-x<100,则x(150-x)+80(100-x)=9200,
解得=30(舍去),=40;
②当40<x<60时,则40<100-x<60,
则x(150-x)+(100-x) [150-(100-x)]=9200,
解得x=30或x=70,但40<x<60,所以无解;
答:第一批购买数量为40件..
15.(1)50(2)若该宿舍5月份交电费45元,那么该宿舍当月用电量为100千瓦时。
解:(1)根据3月份用电80千瓦时,交电费35元,得,
,即。
解得a=30或a=50。
由4月份用电45千瓦时,交电费20元,得,a≥45。
∴a=50。
(2)设月用电量为x千瓦时,交电费y元。则
∵5月份交电费45元,∴5月份用电量超过50千瓦时。
∴45=20+0.5(x-50),解得x=100。
(1)根据3月份用电80千瓦时,交电费35元列出方程求解,结合4月份用电45千瓦时,交电费20元,确定a的范围,从而得出结果。
(2)列出电费y元与用电量x千瓦时的函数关系式,根据5月份交电费45元,代入即可。
16.(1)PQ=6cm;(2)s或s;(3)经过4秒或6秒△PBQ的面积为 12cm2.
解:(1)过点P作PE⊥CD于E.
则根据题意,得
EQ=16-2×3-2×2=6(cm),PE=AD=6cm;
在Rt△PEQ中,根据勾股定理,得
PE2+EQ2=PQ2,即36+36=PQ2,
∴PQ=6cm;
∴经过2s时P、Q两点之间的距离是6cm;
(2)设x秒后,点P和点Q的距离是10cm.
(16-2x-3x)2+62=102,即(16-5x)2=64,
∴16-5x=±8,
∴x1=,x2=;
∴经过s或sP、Q两点之间的距离是10cm;
(3)连接BQ.设经过ys后△PBQ的面积为12cm2.
①当0≤y≤时,则PB=16-3y,
∴PB?BC=12,即×(16-3y)×6=12,
解得y=4;
②当<x≤时,
BP=3y-AB=3y-16,QC=2y,则
BP?CQ=(3y-16)×2y=12,
解得y1=6,y2=-(舍去);
③<x≤8时,
QP=CQ-PQ=22-y,则
QP?CB=(22-y)×6=12,
解得y=18(舍去).
综上所述,经过4秒或6秒△PBQ的面积为 12cm2.
考点:一元二次方程的应用.
17.(1)s=96﹣6t (2)或
解:(1)过点P作PM⊥BC于M,则四边形PDCM为矩形.
∴PM=DC=12,
∵QB=16﹣t,
∴S=QB?PM=(16﹣t)×12=96﹣6t
(2)由图可知,CM=PD=2t,CQ=t,若以B、P、Q为顶点的三角形是等腰三角形,可以分三种情况:
①若PQ=BQ,在Rt△PMQ中,PQ2=t2+122,
由PQ2=BQ2得t2+122=(16﹣t)2,解得t=;
②若BP=BQ,在Rt△PMB中,PB2=(16﹣2t)2+122,由PB2=BQ2得(16﹣2t)2+122=(16﹣t)2,即3t2﹣32t+144=0,
此时,△=(﹣32)2﹣4×3×144=﹣704<0,所以此方程无解,
∴BP≠BQ.
③若PB=PQ,由PB2=PQ2得t2+122=(16﹣2t)2+122得t1=,t2=16(不合题意,舍去).
综上所述,当t=或t=时,以B,P,Q三点为顶点的三角形是等腰三角形.
18.(1)5;(2)180
解:(1)设每轮传染中平均一个人传染了x个人,根据题意得:
x+1+(x+1)x=36,
解得:x=5或x=﹣7(舍去).
答:每轮传染中平均一个人传染了5个人;
(2)根据题意得:5×36=180(个),
答:第三轮将又有180人被传染.
19.(1)证明;(2)5,24;(3)M,N出发秒,秒,秒钟后,△MON的面积为m2.
解:(1)证明:∵AO平分∠BAD,AB∥CD
∴∠DAC=∠BAC=∠DCA
∴△ACD是等腰三角形,AD=DC
又∵AB=AD
∴AB=CD,
∴四边形ABCD为平行四边形,
又∵AB=AD,∴?ABCD是菱形;
(2)解:解方程x2-7x+12=0,得
OA=4,OB=3,
利用勾股定理AB==5,
S菱形ABCD=AC×BD=×8×6=24平方米.
(3)解:在第(2)问的条件下,设M、N同时出发x秒钟后,△MON的面积为m2,
当点M在OA上时,x≤2,S△MON=(4-2x)(3-x)=;
解得x1=,x2=(大于2,舍去);
当点M在OC上且点N在OB上时,2<x<3,S△MON=(3-x)(2x-4)=,
解得x1=x2=;
当点M在OC上且点N在OD上时,即3≤x≤4,S△MON=(2x-4)(x-3)=;
解得x1=,x2=(小于3,舍去).
综上所述:M,N出发秒,秒,秒钟后,△MON的面积为m2.
20.(1)700;(2)10.
解:(1)二娃手机厂9月销售炫酷版手机x部,则实用版抗摔手机(1200-x)部
根据题意得:6600x+3000(1200-x)=6120000
解得x=700.
答:二娃手机厂9月销售炫酷版手机700部;
(2)由题意得:炫酷版摄影手机和实用版抗摔手机10月份的价格分别为:6600-600=6000元,3000(1-m%)元;预估销售量分别为:700(1+),500(1+);
则根据题意得:
6000×700(1+)+3000(1-m%)500(1+)+120000=6120000
化简得:m2-110m+1000=0,解得:m=10或m=100(舍).
答:的值为10.
同课章节目录
- 第1章 一元二次方程
- 1.1 一元二次方程
- 1.2 一元二次方程的解法
- 1.3 一元二次方程的根与系数的关系
- 1.4 用一元二次方程解决问题
- 数学活动 矩形绿地中的花圃设计
- 第2章 对称图形——圆
- 2.1 圆
- 2.2 圆的对称性
- 2.3 确定圆的条件
- 2.4 圆周角
- 2.5 直线与圆的位置关系
- 2.6 正多边形与圆
- 2.7 弧长及扇形的面积
- 2.8 圆锥的侧面积
- 数学活动 图形的密铺
- 第3章 数据的集中趋势和离散程度
- 3.1 平均数
- 3.2 中位数与众数
- 3.3 用计算器求平均数
- 3.4 方差
- 3.5 用计算器求方差
- 数学活动 估测时间
- 第4章 等可能条件下的概率
- 4.1 等可能性
- 4.2 等可能条件下的概率(一)
- 4.3 等可能条件下的概率(二)
- 数学活动 调查“小概率事件”
