2021-2022学年苏科版九年级数学上册《1.2一元二次方程的解法》暑假自主学习培优提升训练(word版含答案)
文档属性
| 名称 | 2021-2022学年苏科版九年级数学上册《1.2一元二次方程的解法》暑假自主学习培优提升训练(word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 681.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-08 08:55:06 | ||
图片预览




文档简介
2021年苏科版九年级数学上册《1.2一元二次方程的解法》暑假自主学习
培优提升训练(附答案)
1.已知实数使关于的反比例函数的图象在第二、四象限,且使关于的方程有实数解,若是整数,则所有满足条件的的值的和为( )
A. B. C.0 D.1
2.对于一元二次方程,有下列说法:
①若,则方程必有一个根为1;
②若方程有两个不相等的实根,则方程必有两个不相等的实根;
③若是方程的一个根,则一定有成立;
④若是一元二次方程的根,则.
其中正确的有( )
A.1个 B.2个 C.3个 D.4个
3.若反比例函数的图像上有两个不同的点关于轴的对称点都在一次函数的图像上,则的取值范围是( )
A. B. C. D.或
4.已知,则等于( )
A.或 B.6或1 C.或1 D.2或3
5.当______,_______时,多项式有最小值,这个最小值是_____.
6.已知矩形的长和宽分别是n和1,其中n是正整数,若存在另一个矩形,它的周长和面积分别是矩形周长和面积的一半,则满足条件的n的最小值是________.
7.三角形两边的长分别是8cm和6cm,第三边的长是方程x2﹣12x+20=0的一个实数根,则三角形的面积是_____.
8.如图,在矩形ABCD中,AB=1,BC=3,AC和BD交于点O,点E是边BC上的动点(不与点B,C重合),连接EO并延长交AD于点F,连接AE,若△AEF是等腰三角形,则DF的长为_____.
9.已知关于的方程,,均为常数,且的两个解是和,则方程的解是____.
10.若关于的一元二次方程的两个不等实数根分别为,且,则的值为_____________.
11.若关于x的方程(a+1)x2+(2a﹣3)x+a﹣2=0有两个不相等的实根,且关于x的方程的解为整数,则满足条件的所有整数a的和是_____.
12.关于x的一元二次方程有两个不等的整数根,m为整数,那么m的值是_________.
13.方程的两个根为、,则的值为________.
14.如图,在平面直角坐标系中,平行四边形OBCD的边OB在x轴正半轴上,反比例函数y=(x>0)的图象经过该平行四边形对角线的交点A,且与边BC交于点F.若点D的坐标为(6,8)且OD=DC,则点F的坐标是________.
15.解方程:
(). ().
16.用适当的方法解方程
(1) (2)
(3) (4)
17.已知关于x的方程x2﹣(2k+1)x+4(k﹣)=0.
(1)求证:无论k为何值时,方程总有两个实数根.
(2)若等腰△ABC的一边长a=4,另两边b、c恰好是这个方程的两个实数根,求△ABC的周长.
18.阅读下面的例题,
范例:解方程x2﹣|x|﹣2=0,
解:(1)当x≥0时,原方程化为x2﹣x﹣2=0,解得:x1=2,x2=﹣1(不合题意,舍去).
(2)当x<0时,原方程化为x2+x﹣2=0,解得:x1=﹣2,x2=1(不合题意,舍去).
∴原方程的根是x1=2,x2=﹣2
请参照例题解方程x2﹣|x﹣10|﹣10=0.
19.阅读下面的解题过程,求的最小值.
解:∵=,
而,即最小值是0;
∴的最小值是5
依照上面解答过程,
(1)求的最小值;
(2)求的最大值.
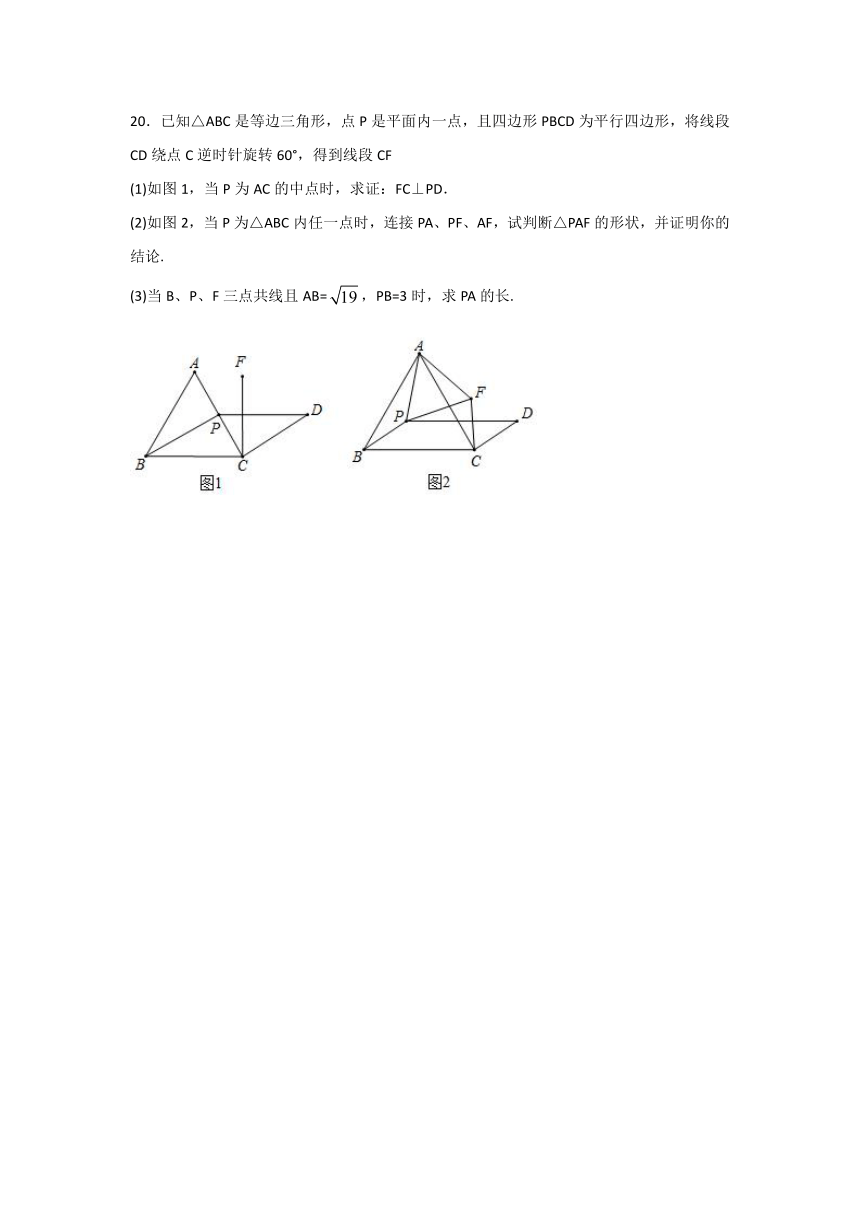
20.已知△ABC是等边三角形,点P是平面内一点,且四边形PBCD为平行四边形,将线段CD绕点C逆时针旋转60°,得到线段CF
(1)如图1,当P为AC的中点时,求证:FC⊥PD.
(2)如图2,当P为△ABC内任一点时,连接PA、PF、AF,试判断△PAF的形状,并证明你的结论.
(3)当B、P、F三点共线且AB=,PB=3时,求PA的长.
参考答案
1 2 3 4
C A D A
5.4 3 15
解:
=
=
=
∴当a=4,b=3时,多项式有最小值15.
故答案为:4,3,15.
6.6
解:设另一个矩形的长和宽分别为: 和 ,
则+=,=,
∴ 和可以看作是关于x的一元二次方程的两个实数根,
即:,解得:或,
∵n是正整数,
∴满足条件的n的最小值是:6,
故答案是:6.
7.24cm2
解:把方程左边因式分解得到(x﹣10)(x﹣2)=0,再把方程化为两个一元一次方程x﹣10=0或x﹣2=0,解得x1=10,x2=2,根据三角形三边的关系得到三角形第三边的长为10,然后计算三角形的周长=×6×8=24cm2.
8.或1或或.
解:∵四边形ABCD是矩形,
∴AD∥BC,OB=OD,
∴∠FDO=∠EBO,∠DFO=∠BEO,
∴△BEO≌△DFO(AAS),
∴OF=OE,DF=BE.
设BE=DF=a,则AF=3﹣a.
当△AEF是等腰三角形时,分三种情况讨论.
①如图(1),当AE=AF时,在Rt△ABE中,由AE2=AB2+BE2,得(3﹣a)2=12+a2,
解得a=
②如图(2),当AE=EF时,过点E作EH⊥AD于点H,则AH=FH=BE,
∴AF=2BE,
∴3﹣a=2a,
解得a=1.
③如图(3),当AF=EF时,∠FAE=∠FEA.
又∠FAE=∠AEB,
∴∠FEA=∠AEB.
过点A作AG⊥EF于点G,则AG=AB=1,EG=BE=a,
∴FG=3﹣2a.
在Rt△AFG中,由AF2=AG2+FG2,得(3﹣a)2=12+(3﹣2a)2,
解得a1=1-, a2=1+.
综上所述,DF的长为或1或1-或1+.
故答案为:或1或1-或1+.
9.,
解:∵关于的方程,,均为常数,且的两个解是和
∴或
∵
∴
∴或
∴或
故答案为:,
10.-5
解:∵关于x的一元二次方程x2﹣3x+a=0(a≠0)的两个不相等的实数根分别为p和q,∴p+q=3,pq=a.
∵,∴(p+q)2﹣3pq=18,∴9﹣3a=18,解得:a=﹣3,即pq=﹣3, ∴====﹣5.
故答案为:﹣5.
11.2
解:∵关于x的方程(a+1)x2+(2a﹣3)x+a﹣2=0有两个不相等的实根,
∴a+1≠0且△=(2a﹣3)2﹣4(a+1)×(a﹣2)>0,
解得a<且a≠﹣1.
把关于x的方程去分母得ax﹣1﹣x=3,
解得
∵x≠﹣1,
∴,解得a≠﹣3,
∵ (a≠﹣3)为整数,
∴a﹣1=±1,±2,±4,
∴a=0,2,﹣1,3,5,﹣3,
而a<且a≠﹣1且a≠﹣3,
∴a的值为0,2,
∴满足条件的所有整数a的和是2.
故答案是:2.
12.-1.
解:∵一元二次方程有两个不等的整数根,
∴△>0,
∴>0,
∴>0,
∴m≠1,
∵,
∴当m>1时,,
∴=1,,
∵一元二次方程有两个不等的整数根,m为整数,
∴m=1,与m≠1矛盾,
∴此种情形不成立;
∴当m<1时,,
∴=,,
∵一元二次方程有两个不等的整数根,m为整数,
∴m=-1,
∴此种情形成立;
综上所述,m的值为-1,
故答案为:-1.
13.
解:∵方程x2+3x+1=0的两个根为α、β,
∴α+β=-3,α?β=1,
∴,,
∴=
故答案为3.
14.(12, )
解:如图,过点D作DM⊥x轴于点M,过点F作FE⊥x于点E,
∵点D的坐标为(6,8),
∴OD=,
∵平行四边形OBCD中OD=DC,
∴四边形OBCD是菱形,
∴OB=OD=10,
∴点B的坐标为(10,0),
∵点A为菱形OBCD对角线的交点,
∴点A是BD的中点,坐标为(8,4),
∵点A在反比例函数y=上,
∴k=xy=8×4=32,
∴反比例函数解析式为y=
∵OD∥BC,OD直线的斜率
∴设BC直线解析式为,将B (10,0)代入解析式得
,解得,
∴BC直线解析式为
点F在BC上,设F点坐标为()
∵点F在反比例函数上,
∴,
即,
解得: , (舍去),
当时,
∴点F的坐标为:(12, ).
故答案为:(12, )
15.(1) ,.(2) ,.
().
解:原式可化为,
,
∴,
∴,.
().
解:,
,
∴,.
16.(1) ;(2);(3) ;(4)
解:(1)
x-1=±6
;
(2)
(x+7)(x+1)=0
;
(3)
移项得
;
(4)
移项得
(x-4+5-2x)(x-4-5+2x)=0
解得
17.解:(1)证明:方程化为一般形式为:x2﹣(2k+1)x+4k﹣2=0,
∵△=(2k+1)2﹣4(4k﹣2)=(2k﹣3)2,
而(2k﹣3)2≥0,
∴△≥0,
所以无论k取任何实数,方程总有两个实数根;
(2)解:x2﹣(2k+1)x+4k﹣2=0,
整理得(x﹣2)[x﹣(2k﹣1)]=0,
∴x1=2,x2=2k﹣1,
当a=4为等腰△ABC的底边,则有b=c,
因为b、c恰是这个方程的两根,则2=2k﹣1,
解得k=,则三角形的三边长分别为:2,2,4,
∵2+2=4,这不满足三角形三边的关系,舍去;
当a=4为等腰△ABC的腰,
因为b、c恰是这个方程的两根,所以只能2k﹣1=4,
则三角形三边长分别为:2,4,4,
此时三角形的周长为2+4+4=10.
所以△ABC的周长为10.
18.x1=4,x2=﹣5.
解:当x≥10时,原方程化为x2﹣x+10﹣10=0,解得x1=0(不合题意,舍去),x2=1(不合题意,舍去);
当x<10时,原方程化为x2+x﹣20=0,解得x3=4,x4=﹣5,
故原方程的根是x1=4,x2=﹣5.
19.(1)2019;(2)5.
解:(1)
∵,
∴,
∴的最小值为2019;
(2)
,
∵,
∴,
∴,
∴的最大值是5.
20.(1)证明:如图1,设FC、PD交于点M,
∵△ABC是等边三角形,P为AC的中点,
∴∠PBC=∠ABC=×60°=30°,
∵四边形PBCD为平行四边形,
∴∠D=∠PBC=30°.
∵∠FCD=60°,
∴∠FCD+∠D=90°,
∴∠CMD=90°,
∴FC⊥PD;
(2)△PAF是等边三角形,理由如下:
如图2,延长BC,∵△ABC为等边三角形,
∴AB=AC,∠ABC=∠ACB=60°,
∴∠2=60°﹣∠1,∠4=180°﹣60°﹣60°﹣∠3=60°﹣∠3.
∵四边形PBCD是平行四边形,
∴PB∥CD,PB=CD=FC.
∴∠1=∠3,∴∠2=∠4.
又AB=AC,PB=FC,
∴△ABP≌△ACF(SAS).
∴AP=AF,∠BAP=∠CAF.
∵∠BAP+∠PAC=60°,
∴∠PAC+∠CAF=∠PAF=60°,
∴△PAF是等边三角形;
(3)①当点P在线段BF上时,如图3,过A作AE⊥BF于E,由(2)可得∠APF=60°,
设PE=x,则AE=x,
于是在Rt△ABE中,根据勾股定理得:,
解得:x1=1,x2=(不合题意,舍去)
∴PA=2x=2;
②当点P落在线段FB的延长线上时,如图4,过B作BE⊥PA于E,
则在Rt△PBE中,PB=3,由(2)可得∠BPE=60°,∴∠PBE=30°.
∴PE=,BE=.
在Rt△ABE中,AB=,BE=,∴AE=,
∴PA=PE+AE=5.
由于P点不可能在线段BF的延长线上,所以, PA的长为2或5.
培优提升训练(附答案)
1.已知实数使关于的反比例函数的图象在第二、四象限,且使关于的方程有实数解,若是整数,则所有满足条件的的值的和为( )
A. B. C.0 D.1
2.对于一元二次方程,有下列说法:
①若,则方程必有一个根为1;
②若方程有两个不相等的实根,则方程必有两个不相等的实根;
③若是方程的一个根,则一定有成立;
④若是一元二次方程的根,则.
其中正确的有( )
A.1个 B.2个 C.3个 D.4个
3.若反比例函数的图像上有两个不同的点关于轴的对称点都在一次函数的图像上,则的取值范围是( )
A. B. C. D.或
4.已知,则等于( )
A.或 B.6或1 C.或1 D.2或3
5.当______,_______时,多项式有最小值,这个最小值是_____.
6.已知矩形的长和宽分别是n和1,其中n是正整数,若存在另一个矩形,它的周长和面积分别是矩形周长和面积的一半,则满足条件的n的最小值是________.
7.三角形两边的长分别是8cm和6cm,第三边的长是方程x2﹣12x+20=0的一个实数根,则三角形的面积是_____.
8.如图,在矩形ABCD中,AB=1,BC=3,AC和BD交于点O,点E是边BC上的动点(不与点B,C重合),连接EO并延长交AD于点F,连接AE,若△AEF是等腰三角形,则DF的长为_____.
9.已知关于的方程,,均为常数,且的两个解是和,则方程的解是____.
10.若关于的一元二次方程的两个不等实数根分别为,且,则的值为_____________.
11.若关于x的方程(a+1)x2+(2a﹣3)x+a﹣2=0有两个不相等的实根,且关于x的方程的解为整数,则满足条件的所有整数a的和是_____.
12.关于x的一元二次方程有两个不等的整数根,m为整数,那么m的值是_________.
13.方程的两个根为、,则的值为________.
14.如图,在平面直角坐标系中,平行四边形OBCD的边OB在x轴正半轴上,反比例函数y=(x>0)的图象经过该平行四边形对角线的交点A,且与边BC交于点F.若点D的坐标为(6,8)且OD=DC,则点F的坐标是________.
15.解方程:
(). ().
16.用适当的方法解方程
(1) (2)
(3) (4)
17.已知关于x的方程x2﹣(2k+1)x+4(k﹣)=0.
(1)求证:无论k为何值时,方程总有两个实数根.
(2)若等腰△ABC的一边长a=4,另两边b、c恰好是这个方程的两个实数根,求△ABC的周长.
18.阅读下面的例题,
范例:解方程x2﹣|x|﹣2=0,
解:(1)当x≥0时,原方程化为x2﹣x﹣2=0,解得:x1=2,x2=﹣1(不合题意,舍去).
(2)当x<0时,原方程化为x2+x﹣2=0,解得:x1=﹣2,x2=1(不合题意,舍去).
∴原方程的根是x1=2,x2=﹣2
请参照例题解方程x2﹣|x﹣10|﹣10=0.
19.阅读下面的解题过程,求的最小值.
解:∵=,
而,即最小值是0;
∴的最小值是5
依照上面解答过程,
(1)求的最小值;
(2)求的最大值.
20.已知△ABC是等边三角形,点P是平面内一点,且四边形PBCD为平行四边形,将线段CD绕点C逆时针旋转60°,得到线段CF
(1)如图1,当P为AC的中点时,求证:FC⊥PD.
(2)如图2,当P为△ABC内任一点时,连接PA、PF、AF,试判断△PAF的形状,并证明你的结论.
(3)当B、P、F三点共线且AB=,PB=3时,求PA的长.
参考答案
1 2 3 4
C A D A
5.4 3 15
解:
=
=
=
∴当a=4,b=3时,多项式有最小值15.
故答案为:4,3,15.
6.6
解:设另一个矩形的长和宽分别为: 和 ,
则+=,=,
∴ 和可以看作是关于x的一元二次方程的两个实数根,
即:,解得:或,
∵n是正整数,
∴满足条件的n的最小值是:6,
故答案是:6.
7.24cm2
解:把方程左边因式分解得到(x﹣10)(x﹣2)=0,再把方程化为两个一元一次方程x﹣10=0或x﹣2=0,解得x1=10,x2=2,根据三角形三边的关系得到三角形第三边的长为10,然后计算三角形的周长=×6×8=24cm2.
8.或1或或.
解:∵四边形ABCD是矩形,
∴AD∥BC,OB=OD,
∴∠FDO=∠EBO,∠DFO=∠BEO,
∴△BEO≌△DFO(AAS),
∴OF=OE,DF=BE.
设BE=DF=a,则AF=3﹣a.
当△AEF是等腰三角形时,分三种情况讨论.
①如图(1),当AE=AF时,在Rt△ABE中,由AE2=AB2+BE2,得(3﹣a)2=12+a2,
解得a=
②如图(2),当AE=EF时,过点E作EH⊥AD于点H,则AH=FH=BE,
∴AF=2BE,
∴3﹣a=2a,
解得a=1.
③如图(3),当AF=EF时,∠FAE=∠FEA.
又∠FAE=∠AEB,
∴∠FEA=∠AEB.
过点A作AG⊥EF于点G,则AG=AB=1,EG=BE=a,
∴FG=3﹣2a.
在Rt△AFG中,由AF2=AG2+FG2,得(3﹣a)2=12+(3﹣2a)2,
解得a1=1-, a2=1+.
综上所述,DF的长为或1或1-或1+.
故答案为:或1或1-或1+.
9.,
解:∵关于的方程,,均为常数,且的两个解是和
∴或
∵
∴
∴或
∴或
故答案为:,
10.-5
解:∵关于x的一元二次方程x2﹣3x+a=0(a≠0)的两个不相等的实数根分别为p和q,∴p+q=3,pq=a.
∵,∴(p+q)2﹣3pq=18,∴9﹣3a=18,解得:a=﹣3,即pq=﹣3, ∴====﹣5.
故答案为:﹣5.
11.2
解:∵关于x的方程(a+1)x2+(2a﹣3)x+a﹣2=0有两个不相等的实根,
∴a+1≠0且△=(2a﹣3)2﹣4(a+1)×(a﹣2)>0,
解得a<且a≠﹣1.
把关于x的方程去分母得ax﹣1﹣x=3,
解得
∵x≠﹣1,
∴,解得a≠﹣3,
∵ (a≠﹣3)为整数,
∴a﹣1=±1,±2,±4,
∴a=0,2,﹣1,3,5,﹣3,
而a<且a≠﹣1且a≠﹣3,
∴a的值为0,2,
∴满足条件的所有整数a的和是2.
故答案是:2.
12.-1.
解:∵一元二次方程有两个不等的整数根,
∴△>0,
∴>0,
∴>0,
∴m≠1,
∵,
∴当m>1时,,
∴=1,,
∵一元二次方程有两个不等的整数根,m为整数,
∴m=1,与m≠1矛盾,
∴此种情形不成立;
∴当m<1时,,
∴=,,
∵一元二次方程有两个不等的整数根,m为整数,
∴m=-1,
∴此种情形成立;
综上所述,m的值为-1,
故答案为:-1.
13.
解:∵方程x2+3x+1=0的两个根为α、β,
∴α+β=-3,α?β=1,
∴,,
∴=
故答案为3.
14.(12, )
解:如图,过点D作DM⊥x轴于点M,过点F作FE⊥x于点E,
∵点D的坐标为(6,8),
∴OD=,
∵平行四边形OBCD中OD=DC,
∴四边形OBCD是菱形,
∴OB=OD=10,
∴点B的坐标为(10,0),
∵点A为菱形OBCD对角线的交点,
∴点A是BD的中点,坐标为(8,4),
∵点A在反比例函数y=上,
∴k=xy=8×4=32,
∴反比例函数解析式为y=
∵OD∥BC,OD直线的斜率
∴设BC直线解析式为,将B (10,0)代入解析式得
,解得,
∴BC直线解析式为
点F在BC上,设F点坐标为()
∵点F在反比例函数上,
∴,
即,
解得: , (舍去),
当时,
∴点F的坐标为:(12, ).
故答案为:(12, )
15.(1) ,.(2) ,.
().
解:原式可化为,
,
∴,
∴,.
().
解:,
,
∴,.
16.(1) ;(2);(3) ;(4)
解:(1)
x-1=±6
;
(2)
(x+7)(x+1)=0
;
(3)
移项得
;
(4)
移项得
(x-4+5-2x)(x-4-5+2x)=0
解得
17.解:(1)证明:方程化为一般形式为:x2﹣(2k+1)x+4k﹣2=0,
∵△=(2k+1)2﹣4(4k﹣2)=(2k﹣3)2,
而(2k﹣3)2≥0,
∴△≥0,
所以无论k取任何实数,方程总有两个实数根;
(2)解:x2﹣(2k+1)x+4k﹣2=0,
整理得(x﹣2)[x﹣(2k﹣1)]=0,
∴x1=2,x2=2k﹣1,
当a=4为等腰△ABC的底边,则有b=c,
因为b、c恰是这个方程的两根,则2=2k﹣1,
解得k=,则三角形的三边长分别为:2,2,4,
∵2+2=4,这不满足三角形三边的关系,舍去;
当a=4为等腰△ABC的腰,
因为b、c恰是这个方程的两根,所以只能2k﹣1=4,
则三角形三边长分别为:2,4,4,
此时三角形的周长为2+4+4=10.
所以△ABC的周长为10.
18.x1=4,x2=﹣5.
解:当x≥10时,原方程化为x2﹣x+10﹣10=0,解得x1=0(不合题意,舍去),x2=1(不合题意,舍去);
当x<10时,原方程化为x2+x﹣20=0,解得x3=4,x4=﹣5,
故原方程的根是x1=4,x2=﹣5.
19.(1)2019;(2)5.
解:(1)
∵,
∴,
∴的最小值为2019;
(2)
,
∵,
∴,
∴,
∴的最大值是5.
20.(1)证明:如图1,设FC、PD交于点M,
∵△ABC是等边三角形,P为AC的中点,
∴∠PBC=∠ABC=×60°=30°,
∵四边形PBCD为平行四边形,
∴∠D=∠PBC=30°.
∵∠FCD=60°,
∴∠FCD+∠D=90°,
∴∠CMD=90°,
∴FC⊥PD;
(2)△PAF是等边三角形,理由如下:
如图2,延长BC,∵△ABC为等边三角形,
∴AB=AC,∠ABC=∠ACB=60°,
∴∠2=60°﹣∠1,∠4=180°﹣60°﹣60°﹣∠3=60°﹣∠3.
∵四边形PBCD是平行四边形,
∴PB∥CD,PB=CD=FC.
∴∠1=∠3,∴∠2=∠4.
又AB=AC,PB=FC,
∴△ABP≌△ACF(SAS).
∴AP=AF,∠BAP=∠CAF.
∵∠BAP+∠PAC=60°,
∴∠PAC+∠CAF=∠PAF=60°,
∴△PAF是等边三角形;
(3)①当点P在线段BF上时,如图3,过A作AE⊥BF于E,由(2)可得∠APF=60°,
设PE=x,则AE=x,
于是在Rt△ABE中,根据勾股定理得:,
解得:x1=1,x2=(不合题意,舍去)
∴PA=2x=2;
②当点P落在线段FB的延长线上时,如图4,过B作BE⊥PA于E,
则在Rt△PBE中,PB=3,由(2)可得∠BPE=60°,∴∠PBE=30°.
∴PE=,BE=.
在Rt△ABE中,AB=,BE=,∴AE=,
∴PA=PE+AE=5.
由于P点不可能在线段BF的延长线上,所以, PA的长为2或5.
同课章节目录
- 第1章 一元二次方程
- 1.1 一元二次方程
- 1.2 一元二次方程的解法
- 1.3 一元二次方程的根与系数的关系
- 1.4 用一元二次方程解决问题
- 数学活动 矩形绿地中的花圃设计
- 第2章 对称图形——圆
- 2.1 圆
- 2.2 圆的对称性
- 2.3 确定圆的条件
- 2.4 圆周角
- 2.5 直线与圆的位置关系
- 2.6 正多边形与圆
- 2.7 弧长及扇形的面积
- 2.8 圆锥的侧面积
- 数学活动 图形的密铺
- 第3章 数据的集中趋势和离散程度
- 3.1 平均数
- 3.2 中位数与众数
- 3.3 用计算器求平均数
- 3.4 方差
- 3.5 用计算器求方差
- 数学活动 估测时间
- 第4章 等可能条件下的概率
- 4.1 等可能性
- 4.2 等可能条件下的概率(一)
- 4.3 等可能条件下的概率(二)
- 数学活动 调查“小概率事件”
