2021年暑假自主学习 九年级数学苏科版上册 第2章 对称图形——圆 2.2 圆的对称性 能力达标训练(Word版 含解析)
文档属性
| 名称 | 2021年暑假自主学习 九年级数学苏科版上册 第2章 对称图形——圆 2.2 圆的对称性 能力达标训练(Word版 含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 425.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-08 07:09:16 | ||
图片预览



文档简介
2021年苏科版九年级数学上册《2.2圆的对称性》暑假自主学习能力达标训练(附答案)
1.点P是⊙O内一点,过点P的最长弦的长为10cm,最短弦的长为6cm,则OP的长为( )
A.3cm B.4cm C.5cm D.6cm
2.如图,⊙O的半径OB为4,OC⊥AB于点D,∠BAC=30°,则OD的长是( )
A. B. C.2 D.3
3.如图,⊙O的直径AB垂直弦CD于点P,且P为半径OB的中点,若CD=6,则直径AB的长为( )
A.2 B.6 C.4 D.6
4.下列四个命题:
①同圆或等圆中,相等的弦所对的弧相等;
②同圆或等圆中,相等的弧所对的弦相等;
③同圆或等圆中,相等的弦的弦心距相等;
④同圆或等圆中,相等的弧所对的圆心角相等.
真命题的个数有( )
A.1个 B.2个 C.3个 D.4个
5.往水平放置的半径为13cm的圆柱形容器内装入一些水以后,截面图如图所示,若水面宽度AB=24cm,则水的最大深度为( )
A.5cm B.8cm C.10cm D.12cm
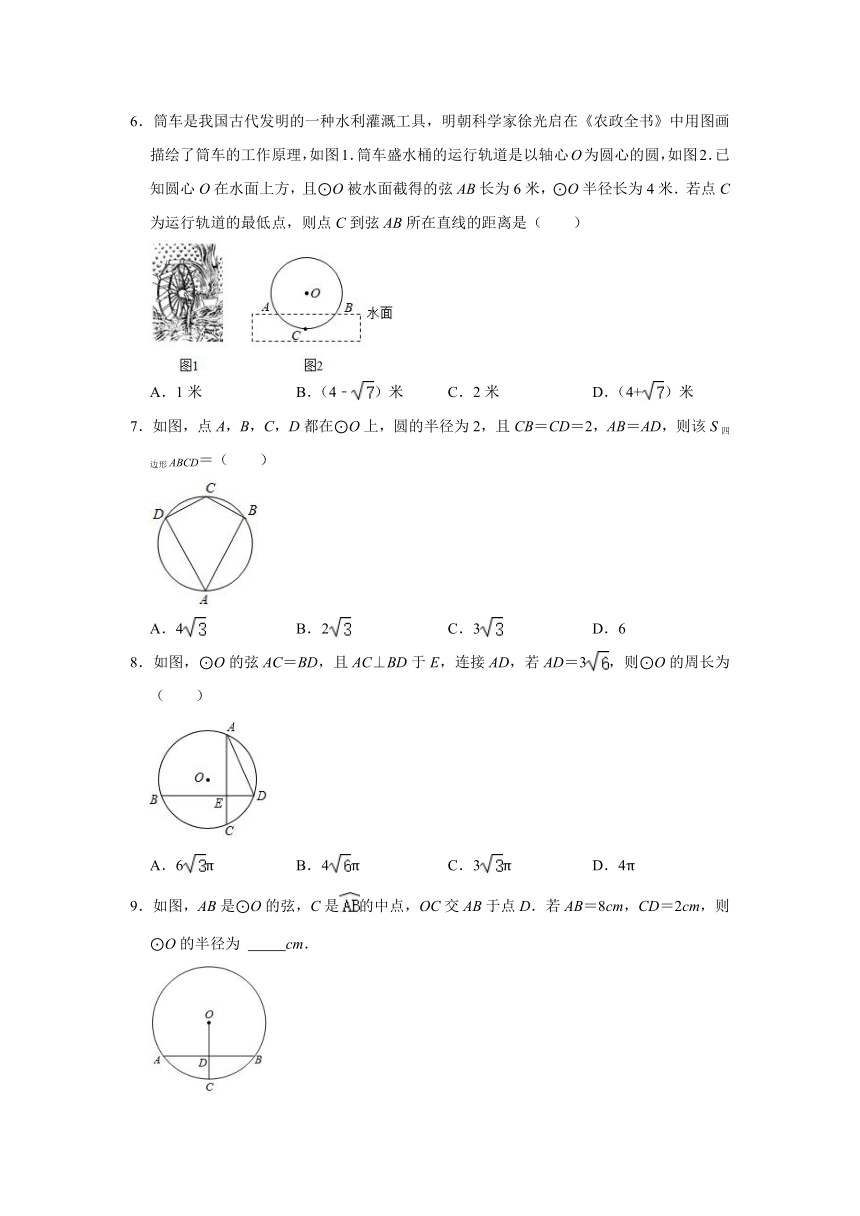
6.筒车是我国古代发明的一种水利灌溉工具,明朝科学家徐光启在《农政全书》中用图画描绘了筒车的工作原理,如图1.筒车盛水桶的运行轨道是以轴心O为圆心的圆,如图2.已知圆心O在水面上方,且⊙O被水面截得的弦AB长为6米,⊙O半径长为4米.若点C为运行轨道的最低点,则点C到弦AB所在直线的距离是( )
A.1米 B.(4﹣)米 C.2米 D.(4+)米
7.如图,点A,B,C,D都在⊙O上,圆的半径为2,且CB=CD=2,AB=AD,则该S四边形ABCD=( )
A.4 B.2 C.3 D.6
8.如图,⊙O的弦AC=BD,且AC⊥BD于E,连接AD,若AD=3,则⊙O的周长为( )
A.6π B.4π C.3π D.4π
9.如图,AB是⊙O的弦,C是的中点,OC交AB于点D.若AB=8cm,CD=2cm,则⊙O的半径为 cm.
10.AB是⊙O的弦,OM⊥AB,垂足为M,连接OA.若∠AOM=60°,OM=,则弦AB的长为 .
11.如图,⊙O的半径OA=15,弦DE⊥AB于点C,若OC:BC=3:2,则DE的长为 .
12.如图,在平面直角坐标系中,⊙O的半径为4,弦AB的长为3,过O作OC⊥AB于点C,则OC的长度是 ,⊙O内一点D的坐标为(﹣2,1),当弦AB绕O点顺时针旋转时,点D到AB的距离的最小值是 ,最大值是 .
13.如图是一种机械传动装置示意图,⊙O的半径为50cm,点A固定在⊙O上,连杆AP定长,点P随着⊙O的转动在射线OP上运动.在一个停止状态时,AP与⊙O交于点B,测得AB=60cm,PB=70cm,此时OP长为 .
14.如图,AB是半圆的直径,C、D是半圆上的两点,且∠BAC=46°,=,则
∠DAB= °.
15.如图,在半径为2的⊙O中,弦AB与弦CD相交于点M,如果AB=CD=2,∠AMC=120°,那么OM的长为 .
16.如图1是博物馆展出的古代车轮实物,《周礼?考工记》记载:“…故兵车之轮六尺有六寸,田车之轮六尺有三时寸…”据此,我们可以通过计算车轮的半径来验证车轮类型.
如图2所示,在车轮上取A、B两点,设所在圆的圆心为O,半径为rcm.作弦AB的垂线OC,D为垂足,经测量,AB=90cm,CD=15cm,则r= cm.通过单位换算,得到车轮直径约为六尺六寸,可验证此车轮为兵车之轮.
17.如图,⊙O的弦AB、CD相交于点P,且AB=CD.求证PB=PD.
18.如图,在⊙O中,弦AB与弦CD相交于点E,且AB=CD.求证:CE=BE.
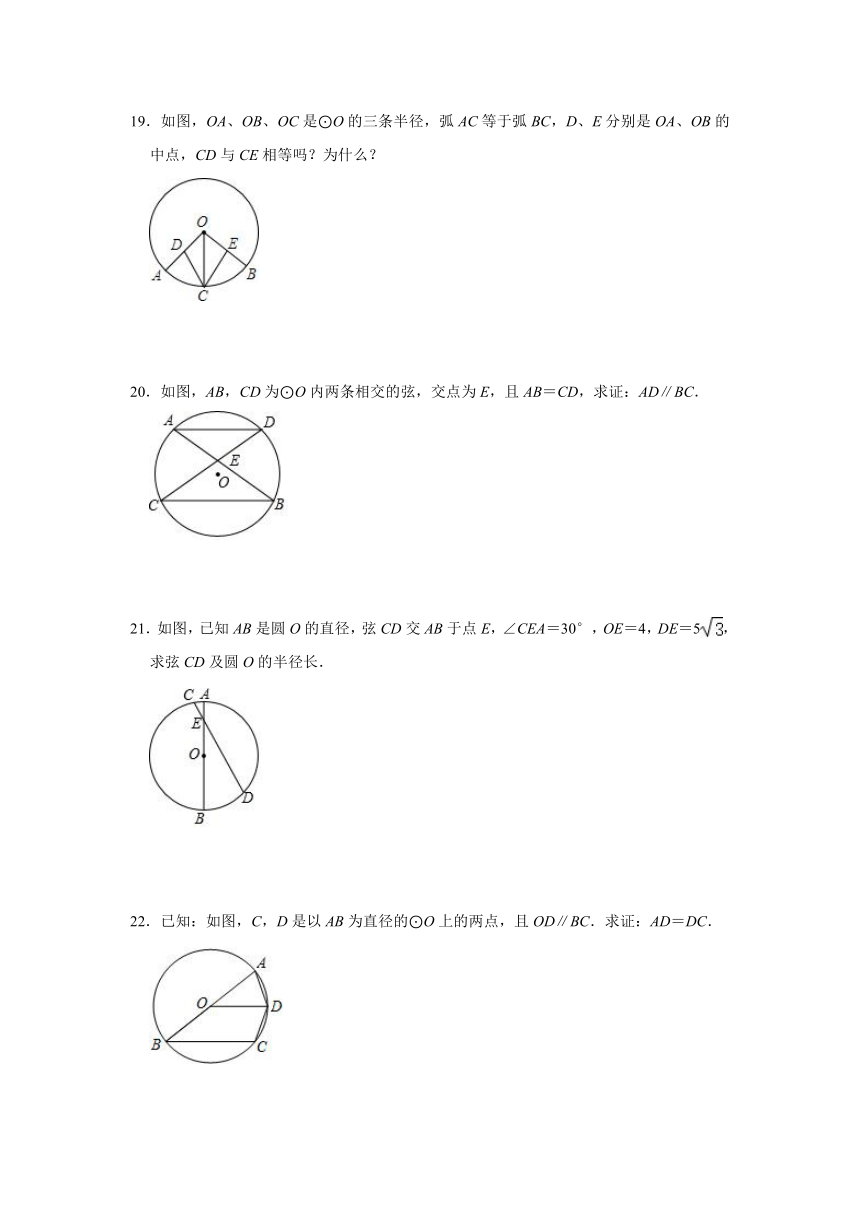
19.如图,OA、OB、OC是⊙O的三条半径,弧AC等于弧BC,D、E分别是OA、OB的中点,CD与CE相等吗?为什么?
20.如图,AB,CD为⊙O内两条相交的弦,交点为E,且AB=CD,求证:AD∥BC.
21.如图,已知AB是圆O的直径,弦CD交AB于点E,∠CEA=30°,OE=4,DE=5,求弦CD及圆O的半径长.
22.已知:如图,C,D是以AB为直径的⊙O上的两点,且OD∥BC.求证:AD=DC.
23.如图,在Rt△ABC中,∠BAC=90°,以点A为圆心,AC长为半径作圆,交BC于点D,交AB于点E,连接DE.
(1)若∠ABC=20°,求∠DEA的度数;
(2)若AC=3,AB=4,求CD的长.
24.如图,AB是⊙O的直径,C是的中点,CE⊥AB于点E,BD交CE于点F.
(1)求证:CF=BF;
(2)若CD=6,AC=8,求⊙O的半径及CE的长.
参考答案
1.解:如图所示,CD⊥AB于点P.
根据题意,得
AB=10cm,CD=6cm.
∵CD⊥AB,
∴CP=CD=3cm.
根据勾股定理,得OP===4(cm).
故选:B.
2.解:连接OA,
∵OC⊥AB,∠BAC=30°,
∴∠ACO=90°﹣30°=60°,
∵OA=OC,
∴△AOC为等边三角形,
∵OC⊥AB,
∴OD=OC=2,
故选:C.
3.解:连接OD,设⊙O的半径为R,
则OP=R,
∵AB⊥CD,CD=6,
∴DP=CP=3,
在Rt△OPD中,由勾股定理得:OD2=OP2+DP2,
R2=(R)2+32,
解得:R=2(负值舍去),
即⊙O的直径AB=4,
故选:C.
4.解:①同圆或等圆中,相等的弦所对的弧相等,错误,是假命题,不符合题意;
②同圆或等圆中,相等的弧所对的弦相等,正确,是真命题,符合题意;
③同圆或等圆中,相等的弦的弦心距相等,正确,是真命题,符合题意;
④同圆或等圆中,相等的弧所对的圆心角相等,正确,是真命题,符合题意,
真命题有3个,
故选:C.
5.解:连接OB,过点O作OC⊥AB于点D,交⊙O于点C,如图所示:
∵AB=24cm,
∴BD=AB=12(cm),
∵OB=OC=13cm,
在Rt△OBD中,OD===5(cm),
∴CD=OC﹣OD=13﹣5=8(cm),
即水的最大深度为8cm,
故选:B.
6.解:连接OC交AB于D,连接OA,
∵点C为运行轨道的最低点,
∴OC⊥AB,
∴AD=AB=3(米),
在Rt△OAD中,OD===(米),
∴点C到弦AB所在直线的距离CD=OC﹣OD=(4﹣)米,
故选:B.
7.解:连接AC,
∵CB=CD,AD=AB,
∴=,=,
∴=,
即AC是圆的直径,
∴∠D=∠B=90°,
∵圆的半径为2,
∴AC=4,
∵CB=CD=2,
由勾股定理得:AD=AB==2,
∴S四边形ABCD
=S△ADC+S△ABC=+=+=4,
故选:A.
8.解:连接AB,AO,DO,
∵⊙O的弦AC=BD,
∴=,
∴=,
∴∠BAC=∠ABD,
∵AC⊥BD,
∴∠AEB=90°,
∴∠ABD=∠BAC=(180°﹣∠AEB)=45°,
∴∠AOD=2∠ABD=90°,
即△AOD是等腰直角三角形,
∵AD=3,AO2+OD2=AD2,
∴AO=3,
∴⊙O的周长是2×π×3=6π,
故选:A.
9.解:如图,连接OA,
∵C是的中点,
∴D是弦AB的中点,
∴OC⊥AB,AD═BD═4,
∵OA═OC,CD═2,
∴OD═OC﹣CD═OA﹣CD,
在Rt△OAD中,
OA2═AD2+OD2,即OA2═16+(OA﹣2)2,
解得OA═5,
故答案为:5.
10.解:∵OM⊥AB,
∴AM=BM,
在Rt△AOM中,∵∠AOM=60°,
∴AM=OM=×=3,
∴AB=2AM=6.
故答案为6.
11.解:连接OD.
∵OA=OB=15,OC:BC=3:2,
∴BC=6,OC=9,
∵AB⊥DE,
∴CD=CE===12,
∴DE=2CD=24,
故答案为:24.
12.解:连接OB,
∵OC⊥AB,
∴BC=AB=,
由勾股定理得,OC==,
由勾股定理得,OD==,
当点D在直线OC上时,点D到AB的距离的最小或最大,
∴点D到AB的距离的最小值为﹣,点D到AB的距离的最大值为+,
故答案为:;﹣;+.
13.解:作OD⊥AB于D,连接OB,
∴AD=BD=AB=30cm,
∴OD===40(cm),
∴PD=PA+AD=70+30=100(cm),
∴OP==20(cm);
故答案为20cm.
方法二:
解:延长PO交圆于E;
∵AB=60cm,PB=70cm,
∴PA=130cm;
由割线定理,得:PB?PA=PC?PD;
设点P到圆心的距离是xcm,则有:
(x﹣50)(x+50)=70×130,
解得x=20cm.
故OP长为20cm.
故答案为20cm.
14.解:∵AB是半圆O的直径,
∴∠ACB=90°,
∵∠BAC=46°,
∴∠B=44°.
∴∠ADC=180°﹣44°=136°.
∵=,
∴AD=DC.
∴∠DAC=∠DCA==22°,
∴∠BAD=∠DAC+∠BAC=22°+46°=68°.
故答案是:68.
15.解:如图,过点O作OE⊥AB,OF⊥CD,垂足为E、F,连接OA,
则AE=BE=AB=,CF=DF=CD=,
在Rt△AOE中,
∵OA=2,AE=,
∴OE==1,
∵AB=CD,
∴OE=OF=1,
又∵OM=OM,
∴Rt△OEM≌Rt△OFM(HL),
∴∠OME=∠OMF=∠AMC=60°,
∴OM=,
故答案为:.
16.解:∵OC⊥AB,AB=90cm,
∴AD=AB=45(cm),
由题意得:OD=(r﹣15)cm,
在Rt△OAD中,由勾股定理得:r2=452+(r﹣15)2,
解得:r=75,
即车轮半径为75cm,
∴车轮直径为150cm,
通过单位换算车轮直径约为六尺六寸,可验证此车轮为兵车之轮.
故答案为:75.
17.证明:连接BD.
∵AB=CD,
∴=
∴﹣=﹣,即=,
∴∠B=∠D,
∴PB=PD.
18.证明:∵AB=CD,
∴=,
∴﹣=﹣,即=,
∴∠C=∠B,
∴CE=BE.
19.解:CD=CE,理由如下:
∵弧AC和弧BC相等,
∴∠AOC=∠BOC,
又∵OA=OB,D、E分别是OA、OB的中点,
∴OD=OE,
在△DOC和△EOC中,
,
∴△DOC≌△EOC(SAS),
∴CD=CE.
20.解:∵AB=CD,
∴=,
∴﹣=﹣,
即=,
∴∠A=∠B,
∴AD∥BC.
21.解:过点O作OM⊥CD于点M,联结OD,
∵∠CEA=30°,∴∠OEM=∠CEA=30°,
在Rt△OEM中,∵OE=4,
∴,
∵,
∴,
∵OM过圆心,OM⊥CD,
∴CD=2DM,
∴,
∵,
∴在Rt△DOM中,,
∴弦CD的长为,⊙O的半径长为.
22.证明:连接OC,如图,
∵OD∥BC,
∴∠1=∠B,∠2=∠3,
又∵OB=OC,
∴∠B=∠3,
∴∠1=∠2,
∴AD=DC.
23.解:(1)如图,连接AD.
∵∠BAC=90°,∠ABC=20°,
∴∠ACD=70°.
∵AC=AD,
∴∠ACD=∠ADC=70°,
∴∠CAD=180°﹣70°﹣70°=40°,
∴∠DAE=90°﹣40°=50°.
又∵AD=AE,
∴.
(2)如图,过点A作AF⊥CD,垂足为F.
∵∠BAC=90°,AC=3,AB=4,
∴BC=5.
又∵?AF?BC=?AC?AB,
∴,
∴.
∵AC=AD,AF⊥CD,
∴.
24.(1)证明:∵AB是⊙O的直径,
∴∠ACB=90°,
∴∠A=90°﹣∠ABC.
∵CE⊥AB,
∴∠CEB=90°,
∴∠ECB=90°﹣∠ABC,
∴∠ECB=∠A.
又∵C是的中点,
∴=,
∴∠DBC=∠A,
∴∠ECB=∠DBC,
∴CF=BF;
(2)解:∵=,
∴BC=CD=6,
∵∠ACB=90°,
∴AB===10,
∴⊙O的半径为5,
∵S△ABC=AB?CE=BC?AC,
∴CE===.
1.点P是⊙O内一点,过点P的最长弦的长为10cm,最短弦的长为6cm,则OP的长为( )
A.3cm B.4cm C.5cm D.6cm
2.如图,⊙O的半径OB为4,OC⊥AB于点D,∠BAC=30°,则OD的长是( )
A. B. C.2 D.3
3.如图,⊙O的直径AB垂直弦CD于点P,且P为半径OB的中点,若CD=6,则直径AB的长为( )
A.2 B.6 C.4 D.6
4.下列四个命题:
①同圆或等圆中,相等的弦所对的弧相等;
②同圆或等圆中,相等的弧所对的弦相等;
③同圆或等圆中,相等的弦的弦心距相等;
④同圆或等圆中,相等的弧所对的圆心角相等.
真命题的个数有( )
A.1个 B.2个 C.3个 D.4个
5.往水平放置的半径为13cm的圆柱形容器内装入一些水以后,截面图如图所示,若水面宽度AB=24cm,则水的最大深度为( )
A.5cm B.8cm C.10cm D.12cm
6.筒车是我国古代发明的一种水利灌溉工具,明朝科学家徐光启在《农政全书》中用图画描绘了筒车的工作原理,如图1.筒车盛水桶的运行轨道是以轴心O为圆心的圆,如图2.已知圆心O在水面上方,且⊙O被水面截得的弦AB长为6米,⊙O半径长为4米.若点C为运行轨道的最低点,则点C到弦AB所在直线的距离是( )
A.1米 B.(4﹣)米 C.2米 D.(4+)米
7.如图,点A,B,C,D都在⊙O上,圆的半径为2,且CB=CD=2,AB=AD,则该S四边形ABCD=( )
A.4 B.2 C.3 D.6
8.如图,⊙O的弦AC=BD,且AC⊥BD于E,连接AD,若AD=3,则⊙O的周长为( )
A.6π B.4π C.3π D.4π
9.如图,AB是⊙O的弦,C是的中点,OC交AB于点D.若AB=8cm,CD=2cm,则⊙O的半径为 cm.
10.AB是⊙O的弦,OM⊥AB,垂足为M,连接OA.若∠AOM=60°,OM=,则弦AB的长为 .
11.如图,⊙O的半径OA=15,弦DE⊥AB于点C,若OC:BC=3:2,则DE的长为 .
12.如图,在平面直角坐标系中,⊙O的半径为4,弦AB的长为3,过O作OC⊥AB于点C,则OC的长度是 ,⊙O内一点D的坐标为(﹣2,1),当弦AB绕O点顺时针旋转时,点D到AB的距离的最小值是 ,最大值是 .
13.如图是一种机械传动装置示意图,⊙O的半径为50cm,点A固定在⊙O上,连杆AP定长,点P随着⊙O的转动在射线OP上运动.在一个停止状态时,AP与⊙O交于点B,测得AB=60cm,PB=70cm,此时OP长为 .
14.如图,AB是半圆的直径,C、D是半圆上的两点,且∠BAC=46°,=,则
∠DAB= °.
15.如图,在半径为2的⊙O中,弦AB与弦CD相交于点M,如果AB=CD=2,∠AMC=120°,那么OM的长为 .
16.如图1是博物馆展出的古代车轮实物,《周礼?考工记》记载:“…故兵车之轮六尺有六寸,田车之轮六尺有三时寸…”据此,我们可以通过计算车轮的半径来验证车轮类型.
如图2所示,在车轮上取A、B两点,设所在圆的圆心为O,半径为rcm.作弦AB的垂线OC,D为垂足,经测量,AB=90cm,CD=15cm,则r= cm.通过单位换算,得到车轮直径约为六尺六寸,可验证此车轮为兵车之轮.
17.如图,⊙O的弦AB、CD相交于点P,且AB=CD.求证PB=PD.
18.如图,在⊙O中,弦AB与弦CD相交于点E,且AB=CD.求证:CE=BE.
19.如图,OA、OB、OC是⊙O的三条半径,弧AC等于弧BC,D、E分别是OA、OB的中点,CD与CE相等吗?为什么?
20.如图,AB,CD为⊙O内两条相交的弦,交点为E,且AB=CD,求证:AD∥BC.
21.如图,已知AB是圆O的直径,弦CD交AB于点E,∠CEA=30°,OE=4,DE=5,求弦CD及圆O的半径长.
22.已知:如图,C,D是以AB为直径的⊙O上的两点,且OD∥BC.求证:AD=DC.
23.如图,在Rt△ABC中,∠BAC=90°,以点A为圆心,AC长为半径作圆,交BC于点D,交AB于点E,连接DE.
(1)若∠ABC=20°,求∠DEA的度数;
(2)若AC=3,AB=4,求CD的长.
24.如图,AB是⊙O的直径,C是的中点,CE⊥AB于点E,BD交CE于点F.
(1)求证:CF=BF;
(2)若CD=6,AC=8,求⊙O的半径及CE的长.
参考答案
1.解:如图所示,CD⊥AB于点P.
根据题意,得
AB=10cm,CD=6cm.
∵CD⊥AB,
∴CP=CD=3cm.
根据勾股定理,得OP===4(cm).
故选:B.
2.解:连接OA,
∵OC⊥AB,∠BAC=30°,
∴∠ACO=90°﹣30°=60°,
∵OA=OC,
∴△AOC为等边三角形,
∵OC⊥AB,
∴OD=OC=2,
故选:C.
3.解:连接OD,设⊙O的半径为R,
则OP=R,
∵AB⊥CD,CD=6,
∴DP=CP=3,
在Rt△OPD中,由勾股定理得:OD2=OP2+DP2,
R2=(R)2+32,
解得:R=2(负值舍去),
即⊙O的直径AB=4,
故选:C.
4.解:①同圆或等圆中,相等的弦所对的弧相等,错误,是假命题,不符合题意;
②同圆或等圆中,相等的弧所对的弦相等,正确,是真命题,符合题意;
③同圆或等圆中,相等的弦的弦心距相等,正确,是真命题,符合题意;
④同圆或等圆中,相等的弧所对的圆心角相等,正确,是真命题,符合题意,
真命题有3个,
故选:C.
5.解:连接OB,过点O作OC⊥AB于点D,交⊙O于点C,如图所示:
∵AB=24cm,
∴BD=AB=12(cm),
∵OB=OC=13cm,
在Rt△OBD中,OD===5(cm),
∴CD=OC﹣OD=13﹣5=8(cm),
即水的最大深度为8cm,
故选:B.
6.解:连接OC交AB于D,连接OA,
∵点C为运行轨道的最低点,
∴OC⊥AB,
∴AD=AB=3(米),
在Rt△OAD中,OD===(米),
∴点C到弦AB所在直线的距离CD=OC﹣OD=(4﹣)米,
故选:B.
7.解:连接AC,
∵CB=CD,AD=AB,
∴=,=,
∴=,
即AC是圆的直径,
∴∠D=∠B=90°,
∵圆的半径为2,
∴AC=4,
∵CB=CD=2,
由勾股定理得:AD=AB==2,
∴S四边形ABCD
=S△ADC+S△ABC=+=+=4,
故选:A.
8.解:连接AB,AO,DO,
∵⊙O的弦AC=BD,
∴=,
∴=,
∴∠BAC=∠ABD,
∵AC⊥BD,
∴∠AEB=90°,
∴∠ABD=∠BAC=(180°﹣∠AEB)=45°,
∴∠AOD=2∠ABD=90°,
即△AOD是等腰直角三角形,
∵AD=3,AO2+OD2=AD2,
∴AO=3,
∴⊙O的周长是2×π×3=6π,
故选:A.
9.解:如图,连接OA,
∵C是的中点,
∴D是弦AB的中点,
∴OC⊥AB,AD═BD═4,
∵OA═OC,CD═2,
∴OD═OC﹣CD═OA﹣CD,
在Rt△OAD中,
OA2═AD2+OD2,即OA2═16+(OA﹣2)2,
解得OA═5,
故答案为:5.
10.解:∵OM⊥AB,
∴AM=BM,
在Rt△AOM中,∵∠AOM=60°,
∴AM=OM=×=3,
∴AB=2AM=6.
故答案为6.
11.解:连接OD.
∵OA=OB=15,OC:BC=3:2,
∴BC=6,OC=9,
∵AB⊥DE,
∴CD=CE===12,
∴DE=2CD=24,
故答案为:24.
12.解:连接OB,
∵OC⊥AB,
∴BC=AB=,
由勾股定理得,OC==,
由勾股定理得,OD==,
当点D在直线OC上时,点D到AB的距离的最小或最大,
∴点D到AB的距离的最小值为﹣,点D到AB的距离的最大值为+,
故答案为:;﹣;+.
13.解:作OD⊥AB于D,连接OB,
∴AD=BD=AB=30cm,
∴OD===40(cm),
∴PD=PA+AD=70+30=100(cm),
∴OP==20(cm);
故答案为20cm.
方法二:
解:延长PO交圆于E;
∵AB=60cm,PB=70cm,
∴PA=130cm;
由割线定理,得:PB?PA=PC?PD;
设点P到圆心的距离是xcm,则有:
(x﹣50)(x+50)=70×130,
解得x=20cm.
故OP长为20cm.
故答案为20cm.
14.解:∵AB是半圆O的直径,
∴∠ACB=90°,
∵∠BAC=46°,
∴∠B=44°.
∴∠ADC=180°﹣44°=136°.
∵=,
∴AD=DC.
∴∠DAC=∠DCA==22°,
∴∠BAD=∠DAC+∠BAC=22°+46°=68°.
故答案是:68.
15.解:如图,过点O作OE⊥AB,OF⊥CD,垂足为E、F,连接OA,
则AE=BE=AB=,CF=DF=CD=,
在Rt△AOE中,
∵OA=2,AE=,
∴OE==1,
∵AB=CD,
∴OE=OF=1,
又∵OM=OM,
∴Rt△OEM≌Rt△OFM(HL),
∴∠OME=∠OMF=∠AMC=60°,
∴OM=,
故答案为:.
16.解:∵OC⊥AB,AB=90cm,
∴AD=AB=45(cm),
由题意得:OD=(r﹣15)cm,
在Rt△OAD中,由勾股定理得:r2=452+(r﹣15)2,
解得:r=75,
即车轮半径为75cm,
∴车轮直径为150cm,
通过单位换算车轮直径约为六尺六寸,可验证此车轮为兵车之轮.
故答案为:75.
17.证明:连接BD.
∵AB=CD,
∴=
∴﹣=﹣,即=,
∴∠B=∠D,
∴PB=PD.
18.证明:∵AB=CD,
∴=,
∴﹣=﹣,即=,
∴∠C=∠B,
∴CE=BE.
19.解:CD=CE,理由如下:
∵弧AC和弧BC相等,
∴∠AOC=∠BOC,
又∵OA=OB,D、E分别是OA、OB的中点,
∴OD=OE,
在△DOC和△EOC中,
,
∴△DOC≌△EOC(SAS),
∴CD=CE.
20.解:∵AB=CD,
∴=,
∴﹣=﹣,
即=,
∴∠A=∠B,
∴AD∥BC.
21.解:过点O作OM⊥CD于点M,联结OD,
∵∠CEA=30°,∴∠OEM=∠CEA=30°,
在Rt△OEM中,∵OE=4,
∴,
∵,
∴,
∵OM过圆心,OM⊥CD,
∴CD=2DM,
∴,
∵,
∴在Rt△DOM中,,
∴弦CD的长为,⊙O的半径长为.
22.证明:连接OC,如图,
∵OD∥BC,
∴∠1=∠B,∠2=∠3,
又∵OB=OC,
∴∠B=∠3,
∴∠1=∠2,
∴AD=DC.
23.解:(1)如图,连接AD.
∵∠BAC=90°,∠ABC=20°,
∴∠ACD=70°.
∵AC=AD,
∴∠ACD=∠ADC=70°,
∴∠CAD=180°﹣70°﹣70°=40°,
∴∠DAE=90°﹣40°=50°.
又∵AD=AE,
∴.
(2)如图,过点A作AF⊥CD,垂足为F.
∵∠BAC=90°,AC=3,AB=4,
∴BC=5.
又∵?AF?BC=?AC?AB,
∴,
∴.
∵AC=AD,AF⊥CD,
∴.
24.(1)证明:∵AB是⊙O的直径,
∴∠ACB=90°,
∴∠A=90°﹣∠ABC.
∵CE⊥AB,
∴∠CEB=90°,
∴∠ECB=90°﹣∠ABC,
∴∠ECB=∠A.
又∵C是的中点,
∴=,
∴∠DBC=∠A,
∴∠ECB=∠DBC,
∴CF=BF;
(2)解:∵=,
∴BC=CD=6,
∵∠ACB=90°,
∴AB===10,
∴⊙O的半径为5,
∵S△ABC=AB?CE=BC?AC,
∴CE===.
同课章节目录
- 第1章 一元二次方程
- 1.1 一元二次方程
- 1.2 一元二次方程的解法
- 1.3 一元二次方程的根与系数的关系
- 1.4 用一元二次方程解决问题
- 数学活动 矩形绿地中的花圃设计
- 第2章 对称图形——圆
- 2.1 圆
- 2.2 圆的对称性
- 2.3 确定圆的条件
- 2.4 圆周角
- 2.5 直线与圆的位置关系
- 2.6 正多边形与圆
- 2.7 弧长及扇形的面积
- 2.8 圆锥的侧面积
- 数学活动 图形的密铺
- 第3章 数据的集中趋势和离散程度
- 3.1 平均数
- 3.2 中位数与众数
- 3.3 用计算器求平均数
- 3.4 方差
- 3.5 用计算器求方差
- 数学活动 估测时间
- 第4章 等可能条件下的概率
- 4.1 等可能性
- 4.2 等可能条件下的概率(一)
- 4.3 等可能条件下的概率(二)
- 数学活动 调查“小概率事件”
