2021年暑假自主学习 九年级数学上册 第2章 对称图形——圆 2.7弧长及扇形面积 能力达标训练(Word版 含解析)
文档属性
| 名称 | 2021年暑假自主学习 九年级数学上册 第2章 对称图形——圆 2.7弧长及扇形面积 能力达标训练(Word版 含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 301.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-08 00:00:00 | ||
图片预览




文档简介
2021年苏科版九年级数学上册《2.7弧长及扇形面积》暑假自主学习能力达标训练(附答案)
1.如图,A、B是⊙O上的两点,∠AOB=120°,OA=3,则劣弧AB的长是( )
A.π B.2π C.3π D.4π
2.若扇形的弧长是5π,半径是18,则该扇形的圆心角是( )
A.50° B.60° C.100° D.120°
3.如图,一块含有30°角的直角三角板ABC,在水平桌面上绕点C按顺时针方向旋转到A′B′C的位置.若BC的长为7.5cm,那么顶点A从开始到结束所经过的路径长为( )
A.10πcm B.10πcm C.15πcm D.20πcm
4.如图,A、B、C是半径为4的⊙O上的三点.如果∠ACB=45°,那么的长为( )
A.π B.2π C.3π D.4π
5.一个商标图案如图中阴影部分,在长方形ABCD中,AB=8cm,BC=4cm,以点A为圆心,AD为半径作圆与BA的延长线相交于点F,则商标图案的面积是( )
A.(4π+8)cm2 B.(4π+16)cm2 C.(3π+8)cm2 D.(3π+16)cm2
6.如图,将边长为3的正方形铁丝框ABCD(面积记为S1)变形为以点B为圆心,BC为半径的扇形(面积记为S2),则S1与S2的关系为( )
A.S1>S2 B.S1=S2 C.S1<S2 D.无法确定
7.如图AB是⊙O的直径,弦CD⊥AB,∠CDB=30°,CD=4,则阴影部分图形的面积为( )
A. B. C.4π D.8π
8.如图,△ABC是等腰直角三角形,以BC为直径,在半径为2(BC=2)且圆心角为90°的扇形内作半圆,交弦AB于点D,则阴影部分的面积是( )
A.π﹣1 B.π﹣2 C.π﹣1 D.π﹣2
9.已知,如图,点C、D在⊙O上,直径AB=6cm,弦AC、BD相交于点E.若CE=BC,则阴影部分面积为( )
A.π﹣ B.π﹣ C.π﹣ D.π﹣
10.如图,AB⊥OB,AB=2,OB=4,把∠ABO绕点O顺时针旋转60°得∠CDO,则AB扫过的面积(图中阴影部分)为( )
A.2 B.2π C. D.π
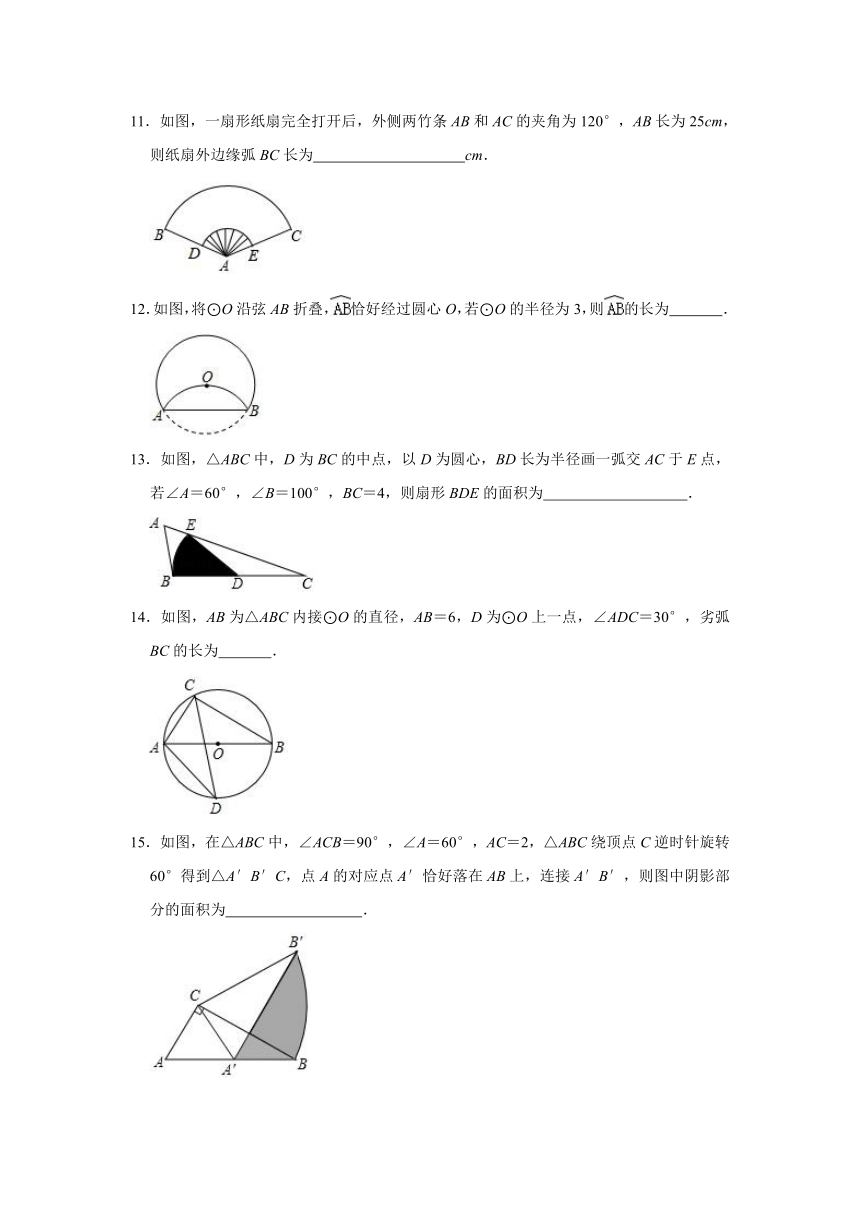
11.如图,一扇形纸扇完全打开后,外侧两竹条AB和AC的夹角为120°,AB长为25cm,则纸扇外边缘弧BC长为 cm.
12.如图,将⊙O沿弦AB折叠,恰好经过圆心O,若⊙O的半径为3,则的长为 .
13.如图,△ABC中,D为BC的中点,以D为圆心,BD长为半径画一弧交AC于E点,若∠A=60°,∠B=100°,BC=4,则扇形BDE的面积为 .
14.如图,AB为△ABC内接⊙O的直径,AB=6,D为⊙O上一点,∠ADC=30°,劣弧BC的长为 .
15.如图,在△ABC中,∠ACB=90°,∠A=60°,AC=2,△ABC绕顶点C逆时针旋转60°得到△A′B′C,点A的对应点A′恰好落在AB上,连接A′B′,则图中阴影部分的面积为 .
16.在△ABC中,∠C为锐角,分别以AB,AC为直径作半圆,过点B,A,C作,如图.若AB=4,AC=2,S1﹣S2=,则S3﹣S4的值是 .
17.如图,AB是⊙O的直径,点C、D均在⊙O上,∠ACD=30°,弦AD=4cm.
(1)求⊙O的直径.
(2)求的长.
18.如图:已知AB为圆O的直径,CD是弦,且AB⊥CD于点E,连接AC,OC,BC.
(1)求证:∠ACO=∠BCD;
(2)若EB=5cm,CD=10cm,求圆O的直径;
(3)求劣弧BC的长.
19.如图,在△ABC中,BA=BC,∠ABC=90°,以AB为直径的半圆O交AC于点D,点E是弧BD上不与B、D重合的任意一点,连接AE交BD于点F,连接BE并延长交AC于点G.
(1)求证:△ADF≌△BDG.
(2)若AB=4,且点E是弧BD的中点,求阴影部分面积.(结果保留π)
20.如图,四边形APBC是圆内接四边形,∠APB=120°,PC平分∠APB,AP,CB的延长线相交于点D.
(1)求证:△ABC是等边三角形;
(2)若∠PAC=90°,AB=2
①求PD的长.
②图中弧BP和线段DP、BD组成的图形面积为 (结果保留π)
21.如图,⊙O的直径AB=16,半径OC⊥AB,D为上一动点(不包括B,C两点),DE⊥OC,DF⊥AB,垂足分别为E,F.
(1)求EF的长.
(2)若点E为OC的中点,
①求劣弧CD的长度;
②若点P为直径AB上一动点,直接写出PC+PD的最小值.
参考答案
1.解:由题意可得,劣弧AB的长是:=2π.
故选:B.
2.解:∵扇形的弧长,
∴5π=,
∴n=50,
∴该扇形的圆心角是50°.
故选:A.
3.解:∵BC=7.5cm,
∴AC=15cm,
=10πcm,
故选:A.
4.解:如图,连接OA、OB.
∵∠ACB=45°,
∴∠AOB=90°,
∵OA=4,
∴的长是:=2π.
故选:B.
5.解:作辅助线DE、EF使BCEF为一矩形.
则S△CEF=(8+4)×4÷2=24cm2,
S正方形ADEF=4×4=16cm2,
S扇形ADF==4πcm2,
∴阴影部分的面积=24﹣(16﹣4π)=8+4π(cm2).
故选:A.
6.解:S1=3×3=9,
∵l扇形=,n=,
∴S2===9,
∴S1=S2.
故选:B.
7.解:∵∠COB=2∠CDB=60°,
又∵CD⊥AB,
∴∠OCB=30°,CE=DE,
∴OE=OC=OB=2,OC=4.
∴OE=BE,
则在△OEC和△BED中,
,
∴△OEC≌△BED,
∴S阴影=S扇形OCB==.
故选:B.
8.解:∵∠ACB=90°,AC=CB,
∴∠CBD=45°,
又∵BC是直径,
∴∠CDB=90°,
∴∠DCB=45°,
∴DC=DB,
∴S弓形CD=S弓形BD,
∴S阴影=S弓形ACB+S△BCD
=S扇形ACB﹣S△ACD
=S扇形ACB﹣S△ABC=π×22﹣××2×2=π﹣1.
故选:A.
9.解:连接OD、OC,
∵AB是直径,
∴∠ACB=90°,
∵CE=BC,
∴∠DBC=∠CEB=45°,
∴的度数为90°,
∴∠DOC=90°,
∴S阴影=S扇形﹣S△ODC=﹣×3×3=﹣.
故选:B.
10.解:∵AB⊥OB,AB=2,OB=4,
∴OA=2,
∴边AB扫过的面积=﹣=π,故选:C.
11.解:纸扇外边缘弧BC的长==(cm),
故答案为:.
12.解:连接OA、OB,作OC⊥AB于C,
由题意得,OC=OA,
∴∠OAC=30°,
∵OA=OB,
∴∠OBA=∠OAC=30°,
∴∠AOB=120°,
∴的长==2π,
故答案为:2π.
13.解:∵∠A=60°,∠B=100°,
∴∠C=180°﹣60°﹣100°=20°,
∵DE=DC,
∴∠C=∠DEC=20°,
∴∠BDE=∠C+∠DEC=40°,
∴S扇形DBE==.
故答案为:.
14.解:如图,连接OC.
∵AB是直径,AB=6,
∴OA=OB=3,
∵∠AOC=2∠ADC=60°,
∴∠BOC=120°,
∴的长==2π,
故答案为:2π.
15.解:过C作CD⊥AB于D,
∵∠ACB=90°,∠A=60°,
∴∠ABC=30°,
∵AC=2,
∴AB=2AC=4,BC===2,
∵S△ABC==,
∴CD===,
∵△ABC绕顶点C逆时针旋转60°得到△A′B′C,
∴B′C=BC=2,AC=A′C=2,∠BCB′=60°,
∵∠A=60°,AC=A′C,
∴△ACA′是等边三角形,
∴AA′=AC=2,
∵AB=4,
∴A′B=4﹣2=2=AA′,
∴阴影部分的面积S=S扇形BCB′+S△BCA′﹣S△A′CB′
=+2×﹣2×2=2π﹣,
故答案为:2π﹣.
16.解:∵AB=4,AC=2,
∴S1+S3=2π,S2+S4=,
∵S1﹣S2=,
∴(S1+S3)﹣(S2+S4)=(S1﹣S2)+(S3﹣S4)=π
∴S3﹣S4=π,
故答案为:π.
17.解:(1)∵AB是⊙O的直径,
∴∠ADB=90°.
∵同弧所对的圆周角相等,
∴∠ABD=∠ACD=30°.
∵AD=4,
∴AB=8.
∴⊙O的直径为8cm.
(2)连接OD,则∠AOD=2∠ACD=60°.
∴的长为.
18.解:(1)∵CE=ED,
∴∠BCD=∠BAC,
∵OA=OC,
∴∠OAC=∠OCA,
∴∠ACO=∠BCD;
(2)设⊙O的半径为Rcm,则OE=OB﹣EB=(R﹣5)cm,
CE=CD=×10=5cm,
在Rt△CEO中,由勾股定理可得:
OC2=OE2+CE2,
即R2=(R﹣5)2+(5)2,
解得R=10.
∴圆O的直径2R=20cm;
(3)在Rt△OEC中,OE=10﹣5=5=OC,
∴∠OCE=30°,
∴∠EOC=60°,
∴劣弧BC的长是=cm.
19.(1)证明:∵AB是⊙O的直径,
∴∠ADB=90°,
∵BA=BC,
∴AD=CD,
∵∠ABC=90°,
∴BD=AD,
在△ADF和△BDG中,
,
∴△ADF≌△BDG(ASA),
(2)解:连接OE,交BD于点H,
∵点E是弧BD的中点,
∴OE⊥BD,
∴OE∥AD,
∴∠BOE=∠BAD=45°,
∵AB=4,
∴OB=OE=2,
在Rt△OHB中,BH=,
∴S阴影=S扇形﹣S△ABE=﹣×=﹣.
20.(1)证明:∵∠APB=120°,PC平分∠APB,
∴∠BPC=∠APC=∠APB=60°,
∴∠BAC=∠BPC=60°.
∵四边形APBC是圆内接四边形,∠APB=120°,
∴∠ACB=180°﹣∠APB=60°,
∴△ABC是等边三角形.
(2)解:①在Rt△PAC中,∠APC=60°,∠PAC=90°,AC=AB=2,
∴∠PCA=30°,
∴PC=2PA.
∵PC2=PA2+AC2,
∴PA=2,PC=4.
同理,可求出CD=4,AD=6,
∴PD=AD﹣PA=4.
②∵∠PAC=90°,四边形APBC是圆内接四边形,
∴∠PBC=90°.
取PC的中点O,连接OB,过点O作OE⊥BC于点E,如图所示,
∴PO=PC=2,OE=PB=PA=1,
∴弧BP和线段DP、BD组成的图形面积=S△PCD﹣S△OBC﹣S扇形POB=×4×2﹣×2×1﹣π×22=3﹣π.
故答案为:3﹣π.
21.解:(1)如图,连接OD,
∵⊙O的直径AB=16,
∴圆的半径为16÷2=8.
∵OC⊥AB,DE⊥OC,DF⊥AB,
∴四边形OFDE是矩形,
∴EF=OD=8.
(2)①∵点E为OC的中点,
∴,
∴∠EDO=30°,
∴∠DOE=60°,
∴劣弧CD的长度为.
②延长CO交⊙O于点G,连接DG交AB于点P,
则PC+PD的最小值为DG.
∵,,
∴
∴PC+PD的最小值为
1.如图,A、B是⊙O上的两点,∠AOB=120°,OA=3,则劣弧AB的长是( )
A.π B.2π C.3π D.4π
2.若扇形的弧长是5π,半径是18,则该扇形的圆心角是( )
A.50° B.60° C.100° D.120°
3.如图,一块含有30°角的直角三角板ABC,在水平桌面上绕点C按顺时针方向旋转到A′B′C的位置.若BC的长为7.5cm,那么顶点A从开始到结束所经过的路径长为( )
A.10πcm B.10πcm C.15πcm D.20πcm
4.如图,A、B、C是半径为4的⊙O上的三点.如果∠ACB=45°,那么的长为( )
A.π B.2π C.3π D.4π
5.一个商标图案如图中阴影部分,在长方形ABCD中,AB=8cm,BC=4cm,以点A为圆心,AD为半径作圆与BA的延长线相交于点F,则商标图案的面积是( )
A.(4π+8)cm2 B.(4π+16)cm2 C.(3π+8)cm2 D.(3π+16)cm2
6.如图,将边长为3的正方形铁丝框ABCD(面积记为S1)变形为以点B为圆心,BC为半径的扇形(面积记为S2),则S1与S2的关系为( )
A.S1>S2 B.S1=S2 C.S1<S2 D.无法确定
7.如图AB是⊙O的直径,弦CD⊥AB,∠CDB=30°,CD=4,则阴影部分图形的面积为( )
A. B. C.4π D.8π
8.如图,△ABC是等腰直角三角形,以BC为直径,在半径为2(BC=2)且圆心角为90°的扇形内作半圆,交弦AB于点D,则阴影部分的面积是( )
A.π﹣1 B.π﹣2 C.π﹣1 D.π﹣2
9.已知,如图,点C、D在⊙O上,直径AB=6cm,弦AC、BD相交于点E.若CE=BC,则阴影部分面积为( )
A.π﹣ B.π﹣ C.π﹣ D.π﹣
10.如图,AB⊥OB,AB=2,OB=4,把∠ABO绕点O顺时针旋转60°得∠CDO,则AB扫过的面积(图中阴影部分)为( )
A.2 B.2π C. D.π
11.如图,一扇形纸扇完全打开后,外侧两竹条AB和AC的夹角为120°,AB长为25cm,则纸扇外边缘弧BC长为 cm.
12.如图,将⊙O沿弦AB折叠,恰好经过圆心O,若⊙O的半径为3,则的长为 .
13.如图,△ABC中,D为BC的中点,以D为圆心,BD长为半径画一弧交AC于E点,若∠A=60°,∠B=100°,BC=4,则扇形BDE的面积为 .
14.如图,AB为△ABC内接⊙O的直径,AB=6,D为⊙O上一点,∠ADC=30°,劣弧BC的长为 .
15.如图,在△ABC中,∠ACB=90°,∠A=60°,AC=2,△ABC绕顶点C逆时针旋转60°得到△A′B′C,点A的对应点A′恰好落在AB上,连接A′B′,则图中阴影部分的面积为 .
16.在△ABC中,∠C为锐角,分别以AB,AC为直径作半圆,过点B,A,C作,如图.若AB=4,AC=2,S1﹣S2=,则S3﹣S4的值是 .
17.如图,AB是⊙O的直径,点C、D均在⊙O上,∠ACD=30°,弦AD=4cm.
(1)求⊙O的直径.
(2)求的长.
18.如图:已知AB为圆O的直径,CD是弦,且AB⊥CD于点E,连接AC,OC,BC.
(1)求证:∠ACO=∠BCD;
(2)若EB=5cm,CD=10cm,求圆O的直径;
(3)求劣弧BC的长.
19.如图,在△ABC中,BA=BC,∠ABC=90°,以AB为直径的半圆O交AC于点D,点E是弧BD上不与B、D重合的任意一点,连接AE交BD于点F,连接BE并延长交AC于点G.
(1)求证:△ADF≌△BDG.
(2)若AB=4,且点E是弧BD的中点,求阴影部分面积.(结果保留π)
20.如图,四边形APBC是圆内接四边形,∠APB=120°,PC平分∠APB,AP,CB的延长线相交于点D.
(1)求证:△ABC是等边三角形;
(2)若∠PAC=90°,AB=2
①求PD的长.
②图中弧BP和线段DP、BD组成的图形面积为 (结果保留π)
21.如图,⊙O的直径AB=16,半径OC⊥AB,D为上一动点(不包括B,C两点),DE⊥OC,DF⊥AB,垂足分别为E,F.
(1)求EF的长.
(2)若点E为OC的中点,
①求劣弧CD的长度;
②若点P为直径AB上一动点,直接写出PC+PD的最小值.
参考答案
1.解:由题意可得,劣弧AB的长是:=2π.
故选:B.
2.解:∵扇形的弧长,
∴5π=,
∴n=50,
∴该扇形的圆心角是50°.
故选:A.
3.解:∵BC=7.5cm,
∴AC=15cm,
=10πcm,
故选:A.
4.解:如图,连接OA、OB.
∵∠ACB=45°,
∴∠AOB=90°,
∵OA=4,
∴的长是:=2π.
故选:B.
5.解:作辅助线DE、EF使BCEF为一矩形.
则S△CEF=(8+4)×4÷2=24cm2,
S正方形ADEF=4×4=16cm2,
S扇形ADF==4πcm2,
∴阴影部分的面积=24﹣(16﹣4π)=8+4π(cm2).
故选:A.
6.解:S1=3×3=9,
∵l扇形=,n=,
∴S2===9,
∴S1=S2.
故选:B.
7.解:∵∠COB=2∠CDB=60°,
又∵CD⊥AB,
∴∠OCB=30°,CE=DE,
∴OE=OC=OB=2,OC=4.
∴OE=BE,
则在△OEC和△BED中,
,
∴△OEC≌△BED,
∴S阴影=S扇形OCB==.
故选:B.
8.解:∵∠ACB=90°,AC=CB,
∴∠CBD=45°,
又∵BC是直径,
∴∠CDB=90°,
∴∠DCB=45°,
∴DC=DB,
∴S弓形CD=S弓形BD,
∴S阴影=S弓形ACB+S△BCD
=S扇形ACB﹣S△ACD
=S扇形ACB﹣S△ABC=π×22﹣××2×2=π﹣1.
故选:A.
9.解:连接OD、OC,
∵AB是直径,
∴∠ACB=90°,
∵CE=BC,
∴∠DBC=∠CEB=45°,
∴的度数为90°,
∴∠DOC=90°,
∴S阴影=S扇形﹣S△ODC=﹣×3×3=﹣.
故选:B.
10.解:∵AB⊥OB,AB=2,OB=4,
∴OA=2,
∴边AB扫过的面积=﹣=π,故选:C.
11.解:纸扇外边缘弧BC的长==(cm),
故答案为:.
12.解:连接OA、OB,作OC⊥AB于C,
由题意得,OC=OA,
∴∠OAC=30°,
∵OA=OB,
∴∠OBA=∠OAC=30°,
∴∠AOB=120°,
∴的长==2π,
故答案为:2π.
13.解:∵∠A=60°,∠B=100°,
∴∠C=180°﹣60°﹣100°=20°,
∵DE=DC,
∴∠C=∠DEC=20°,
∴∠BDE=∠C+∠DEC=40°,
∴S扇形DBE==.
故答案为:.
14.解:如图,连接OC.
∵AB是直径,AB=6,
∴OA=OB=3,
∵∠AOC=2∠ADC=60°,
∴∠BOC=120°,
∴的长==2π,
故答案为:2π.
15.解:过C作CD⊥AB于D,
∵∠ACB=90°,∠A=60°,
∴∠ABC=30°,
∵AC=2,
∴AB=2AC=4,BC===2,
∵S△ABC==,
∴CD===,
∵△ABC绕顶点C逆时针旋转60°得到△A′B′C,
∴B′C=BC=2,AC=A′C=2,∠BCB′=60°,
∵∠A=60°,AC=A′C,
∴△ACA′是等边三角形,
∴AA′=AC=2,
∵AB=4,
∴A′B=4﹣2=2=AA′,
∴阴影部分的面积S=S扇形BCB′+S△BCA′﹣S△A′CB′
=+2×﹣2×2=2π﹣,
故答案为:2π﹣.
16.解:∵AB=4,AC=2,
∴S1+S3=2π,S2+S4=,
∵S1﹣S2=,
∴(S1+S3)﹣(S2+S4)=(S1﹣S2)+(S3﹣S4)=π
∴S3﹣S4=π,
故答案为:π.
17.解:(1)∵AB是⊙O的直径,
∴∠ADB=90°.
∵同弧所对的圆周角相等,
∴∠ABD=∠ACD=30°.
∵AD=4,
∴AB=8.
∴⊙O的直径为8cm.
(2)连接OD,则∠AOD=2∠ACD=60°.
∴的长为.
18.解:(1)∵CE=ED,
∴∠BCD=∠BAC,
∵OA=OC,
∴∠OAC=∠OCA,
∴∠ACO=∠BCD;
(2)设⊙O的半径为Rcm,则OE=OB﹣EB=(R﹣5)cm,
CE=CD=×10=5cm,
在Rt△CEO中,由勾股定理可得:
OC2=OE2+CE2,
即R2=(R﹣5)2+(5)2,
解得R=10.
∴圆O的直径2R=20cm;
(3)在Rt△OEC中,OE=10﹣5=5=OC,
∴∠OCE=30°,
∴∠EOC=60°,
∴劣弧BC的长是=cm.
19.(1)证明:∵AB是⊙O的直径,
∴∠ADB=90°,
∵BA=BC,
∴AD=CD,
∵∠ABC=90°,
∴BD=AD,
在△ADF和△BDG中,
,
∴△ADF≌△BDG(ASA),
(2)解:连接OE,交BD于点H,
∵点E是弧BD的中点,
∴OE⊥BD,
∴OE∥AD,
∴∠BOE=∠BAD=45°,
∵AB=4,
∴OB=OE=2,
在Rt△OHB中,BH=,
∴S阴影=S扇形﹣S△ABE=﹣×=﹣.
20.(1)证明:∵∠APB=120°,PC平分∠APB,
∴∠BPC=∠APC=∠APB=60°,
∴∠BAC=∠BPC=60°.
∵四边形APBC是圆内接四边形,∠APB=120°,
∴∠ACB=180°﹣∠APB=60°,
∴△ABC是等边三角形.
(2)解:①在Rt△PAC中,∠APC=60°,∠PAC=90°,AC=AB=2,
∴∠PCA=30°,
∴PC=2PA.
∵PC2=PA2+AC2,
∴PA=2,PC=4.
同理,可求出CD=4,AD=6,
∴PD=AD﹣PA=4.
②∵∠PAC=90°,四边形APBC是圆内接四边形,
∴∠PBC=90°.
取PC的中点O,连接OB,过点O作OE⊥BC于点E,如图所示,
∴PO=PC=2,OE=PB=PA=1,
∴弧BP和线段DP、BD组成的图形面积=S△PCD﹣S△OBC﹣S扇形POB=×4×2﹣×2×1﹣π×22=3﹣π.
故答案为:3﹣π.
21.解:(1)如图,连接OD,
∵⊙O的直径AB=16,
∴圆的半径为16÷2=8.
∵OC⊥AB,DE⊥OC,DF⊥AB,
∴四边形OFDE是矩形,
∴EF=OD=8.
(2)①∵点E为OC的中点,
∴,
∴∠EDO=30°,
∴∠DOE=60°,
∴劣弧CD的长度为.
②延长CO交⊙O于点G,连接DG交AB于点P,
则PC+PD的最小值为DG.
∵,,
∴
∴PC+PD的最小值为
同课章节目录
- 第1章 一元二次方程
- 1.1 一元二次方程
- 1.2 一元二次方程的解法
- 1.3 一元二次方程的根与系数的关系
- 1.4 用一元二次方程解决问题
- 数学活动 矩形绿地中的花圃设计
- 第2章 对称图形——圆
- 2.1 圆
- 2.2 圆的对称性
- 2.3 确定圆的条件
- 2.4 圆周角
- 2.5 直线与圆的位置关系
- 2.6 正多边形与圆
- 2.7 弧长及扇形的面积
- 2.8 圆锥的侧面积
- 数学活动 图形的密铺
- 第3章 数据的集中趋势和离散程度
- 3.1 平均数
- 3.2 中位数与众数
- 3.3 用计算器求平均数
- 3.4 方差
- 3.5 用计算器求方差
- 数学活动 估测时间
- 第4章 等可能条件下的概率
- 4.1 等可能性
- 4.2 等可能条件下的概率(一)
- 4.3 等可能条件下的概率(二)
- 数学活动 调查“小概率事件”
