青岛版六三制六年级上册五完美的图形——圆信息窗2 圆的周长及应用课件(31张PPT)
文档属性
| 名称 | 青岛版六三制六年级上册五完美的图形——圆信息窗2 圆的周长及应用课件(31张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 3.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-07 17:06:49 | ||
图片预览






文档简介
圆的周长及应用
青岛版数学六年级(上)
五 完美的图形
——圆
结合已学的知识明确什么是圆的周长。
通过测量和计算,了解圆的周长与直径的比为定值,理解圆周率的意义,推出圆的周长公式,并会运用公式解决现实问题。
在探索圆的周长的计算公式的过程中,建立“现实问题—数学问题—联想已有经验—寻求方法—归纳总结—解释应用”的“模型化”思想。
【重点】
理解圆周率的意义,掌握圆的周长的计算方法。
【难点】
圆的周长公式的推导。
围成它们的四条线段的总长度就是它们的周长。
长方形、正方形的周长各指什么,怎么计算?
今天学习新的知识:圆的周长及其计算方法。
正方形的周长=边长×4
长方形的周长=(长+宽)×2
天坛主要由圜(yuán)丘和祈谷(祈年殿)两坛组成。
圜丘坛俗称祭天台,共有三层。上层圆台的直径30米,中层直径是50米,下层直径是70米。
根据这些信息,你能提出什么问题?
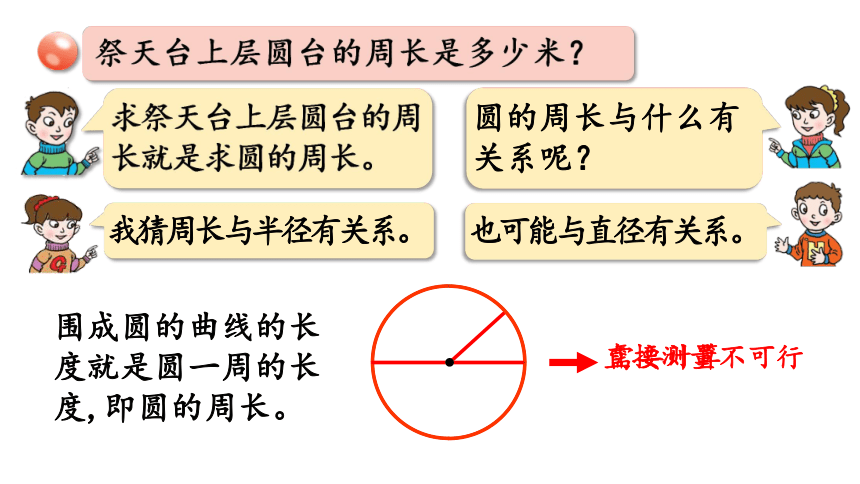
围成圆的曲线的长度就是圆一周的长度,即圆的周长。
直接测量不可行
需要计算
祭天台上层圆台的周长是多少米?
求祭天台上层圆台的周长就是求圆的周长。
圆的周长与什么有关系呢?
我猜周长与半径有关系。
也可能与直径有关系。
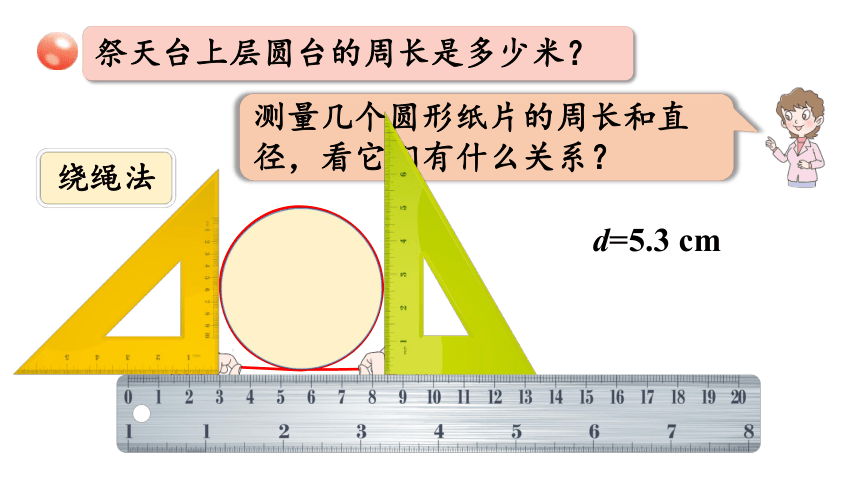
祭天台上层圆台的周长是多少米?
测量几个圆形纸片的周长和直径,看它们有什么关系?
d=5.3 cm
绕绳法
祭天台上层圆台的周长是多少米?
测量几个圆形纸片的周长和直径,看它们有什么关系?
绕绳法
周长为16.5 cm
d=5.3 cm
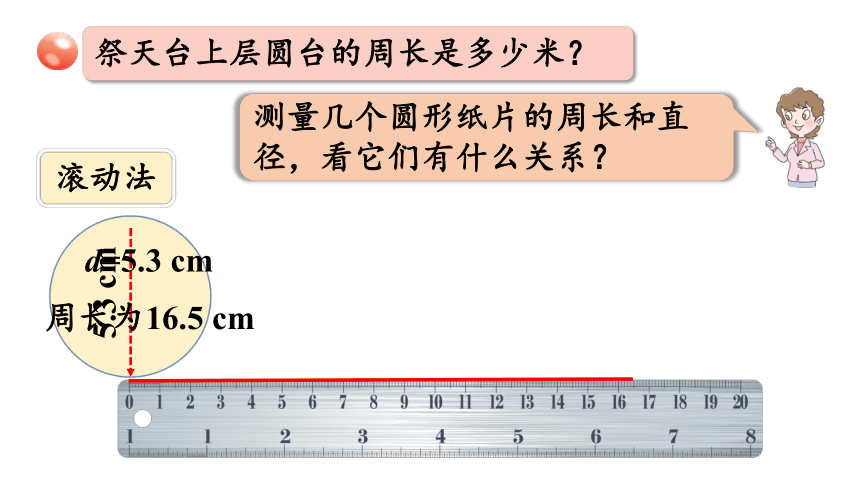
祭天台上层圆台的周长是多少米?
测量几个圆形纸片的周长和直径,看它们有什么关系?
滚动法
5.3 cm
d=5.3 cm
周长为16.5 cm
祭天台上层圆台的周长是多少米?
测量几个圆形纸片的周长和直径,看它们有什么关系?
{16D9F66E-5EB9-4882-86FB-DCBF35E3C3E4}物体
制片1
纸片2
纸片3
周长(cm)
直径(cm)
的比值(保留两位小数)
周长
直径
祭天台上层圆台的周长是多少米?
测量几个圆形纸片的周长和直径,看它们有什么关系?
圆的周长大约是直径的3倍。
我发现圆的直径越大,周长就越大;直径越小,周长就越小。
早在约2100年前,我国古代的数学著作《周髀算经》中就有“周三径一”的说法,意思就说圆的周长是它的直径的3倍。
经过长时间的研究,人们发现,圆的周长和它的直径的比值是一个固定的数,这个比值就叫圆周率,用字母π(pài)表示。
圆周率是一个无限不循环小数:π?=3.1415926535…,在实际的应用中,一般取它的近似值,即π ≈3.14。
?
你知道吗
南北朝时期的祖冲之是我国伟大的数学家和天文学家。祖冲之博学多才,尤其是在数学方面很有天赋。他的重大成就之一是早在约1500年前就计算出圆周率在3.1415926和3.1415927之间,成为世界上第一个把圆周率的值精确到7位小数的人。他的这一辉煌成就比欧洲至少要早1000年。现在,人们已经能用计算机把圆周率计算到小数点后面上千亿位。
祖冲之
你知道吗
如果用C表示圆的周长,你能写出圆周长的计算公式吗。
圆的周长÷直径=圆周率
圆的周长= 圆周率×直径
C=πd
C=2πr
3.14×30=94.2(米)
答:祭天台上层的周长是94.2米。
祭天台上层圆台的周长是多少米?
我会计算祭天台上层圆台的周长了,可以用圆周长的计算公式C=πd直接计算。
祈年殿殿顶周长是100米。
祈年殿殿顶的直径是多少米?
根据C=πd,我列方程解答。
除不尽时,得数一般保留两位小数。
x×3.14=100
解:设祈年殿殿顶的直径是x米。
答:祈年殿殿顶的直径约是31.85米。
x ×3.14÷3.14=100÷3.14
x ≈31.85
祈年殿殿顶周长是100米。
祈年殿殿顶的直径是多少米?
我根据C=πd推出d=C÷π,直接用推出的公式计算。
答:祈年殿殿顶的直径约是31.85米。
100÷3.14 ≈31.85(米)
圆的周长的一半
圆的直径
圆的周长的一半
半圆的周长不仅包括圆周长的一半,还包括直径的长度。
火眼金睛辨对错。
1
(1)圆周率就是3.14。 ( )
圆周率是一个无限不循环小数,在实际应用中,一般取它的近似值3.14。
×
(2)半圆的周长就是圆周长的一半。 ( )
×
3.14×(12×2)
=3.14×24
=75.36(厘米)
3.14×(18×2)
=3.14×36
=113.04(厘米)
答:时针走一圈,它的尖端走过的路程是75.36厘米。
分针走一小时,它的尖端走过的路程是113.04厘米。
(教材第63页“自主练习”第3题 )
2
时针
走一圈
走1小时
分针
长12厘米,如果 ,它的尖端走过的路程是多少? 长 18 厘米,如果 ,它的尖端走过的路程是多少厘米?
圆的半径(r)
圆的直径(d)
圆的周长(C)
2
9
18.84
4
12.56
4.5
28.26
6
3
(教材第63页“自主练习”第4题 )
请将表格补充完整。(单位:米)
3
(1) 3.14×5÷2
=15.7÷2
=7.85(米)
答:需要7.85米篱笆。
(2) 3.14×(5+2)÷2
=21.98÷2
10.99-7.85=3.14(米)
答:需要增加3.14米篱笆。
(教材第64页“自主练习”第8题 )
如图,依墙而建的鸡舍围成半圆形,其直径为
5米。
(1)需要多长的篱笆?
(2)如果将鸡舍的直径增加2米,
需要增加多长的篱笆?
4
=10.99(米)
1.57×40÷3.14÷2
=62.8÷3.14÷2
=20÷2
答:这个水池的半径是10米。
=10(米)
间隔
(教材第64页“自主练习”第10题 )
圆形水池四周种了40棵树,每两棵树之间的距离是1.57米,这个水池的半径是多少米?
4
以8棵树为例画示意图分析:
从图中可以看出,树的棵数=间隔数。
正确解答
围成圆的曲线的长度就是圆一周的长度,即圆的周长。
我明确了圆周长的意义。
同学们,这节课你们学会了哪些知识?
圆的周长= 圆周率×直径 C= πd
圆的周长= 圆周率×半径×2 C= 2πr
圆的直径= 圆的周长÷圆周率 d=C÷π
圆的半径=圆的周长÷圆周率÷2 r=C÷π÷2
我知道了圆周长的计算公式和推导公式。
同学们,这节课你们学会了哪些知识?
相关练习。
02
01
自主练习第1、2、5、6题。
青岛版数学六年级(上)
五 完美的图形
——圆
结合已学的知识明确什么是圆的周长。
通过测量和计算,了解圆的周长与直径的比为定值,理解圆周率的意义,推出圆的周长公式,并会运用公式解决现实问题。
在探索圆的周长的计算公式的过程中,建立“现实问题—数学问题—联想已有经验—寻求方法—归纳总结—解释应用”的“模型化”思想。
【重点】
理解圆周率的意义,掌握圆的周长的计算方法。
【难点】
圆的周长公式的推导。
围成它们的四条线段的总长度就是它们的周长。
长方形、正方形的周长各指什么,怎么计算?
今天学习新的知识:圆的周长及其计算方法。
正方形的周长=边长×4
长方形的周长=(长+宽)×2
天坛主要由圜(yuán)丘和祈谷(祈年殿)两坛组成。
圜丘坛俗称祭天台,共有三层。上层圆台的直径30米,中层直径是50米,下层直径是70米。
根据这些信息,你能提出什么问题?
围成圆的曲线的长度就是圆一周的长度,即圆的周长。
直接测量不可行
需要计算
祭天台上层圆台的周长是多少米?
求祭天台上层圆台的周长就是求圆的周长。
圆的周长与什么有关系呢?
我猜周长与半径有关系。
也可能与直径有关系。
祭天台上层圆台的周长是多少米?
测量几个圆形纸片的周长和直径,看它们有什么关系?
d=5.3 cm
绕绳法
祭天台上层圆台的周长是多少米?
测量几个圆形纸片的周长和直径,看它们有什么关系?
绕绳法
周长为16.5 cm
d=5.3 cm
祭天台上层圆台的周长是多少米?
测量几个圆形纸片的周长和直径,看它们有什么关系?
滚动法
5.3 cm
d=5.3 cm
周长为16.5 cm
祭天台上层圆台的周长是多少米?
测量几个圆形纸片的周长和直径,看它们有什么关系?
{16D9F66E-5EB9-4882-86FB-DCBF35E3C3E4}物体
制片1
纸片2
纸片3
周长(cm)
直径(cm)
的比值(保留两位小数)
周长
直径
祭天台上层圆台的周长是多少米?
测量几个圆形纸片的周长和直径,看它们有什么关系?
圆的周长大约是直径的3倍。
我发现圆的直径越大,周长就越大;直径越小,周长就越小。
早在约2100年前,我国古代的数学著作《周髀算经》中就有“周三径一”的说法,意思就说圆的周长是它的直径的3倍。
经过长时间的研究,人们发现,圆的周长和它的直径的比值是一个固定的数,这个比值就叫圆周率,用字母π(pài)表示。
圆周率是一个无限不循环小数:π?=3.1415926535…,在实际的应用中,一般取它的近似值,即π ≈3.14。
?
你知道吗
南北朝时期的祖冲之是我国伟大的数学家和天文学家。祖冲之博学多才,尤其是在数学方面很有天赋。他的重大成就之一是早在约1500年前就计算出圆周率在3.1415926和3.1415927之间,成为世界上第一个把圆周率的值精确到7位小数的人。他的这一辉煌成就比欧洲至少要早1000年。现在,人们已经能用计算机把圆周率计算到小数点后面上千亿位。
祖冲之
你知道吗
如果用C表示圆的周长,你能写出圆周长的计算公式吗。
圆的周长÷直径=圆周率
圆的周长= 圆周率×直径
C=πd
C=2πr
3.14×30=94.2(米)
答:祭天台上层的周长是94.2米。
祭天台上层圆台的周长是多少米?
我会计算祭天台上层圆台的周长了,可以用圆周长的计算公式C=πd直接计算。
祈年殿殿顶周长是100米。
祈年殿殿顶的直径是多少米?
根据C=πd,我列方程解答。
除不尽时,得数一般保留两位小数。
x×3.14=100
解:设祈年殿殿顶的直径是x米。
答:祈年殿殿顶的直径约是31.85米。
x ×3.14÷3.14=100÷3.14
x ≈31.85
祈年殿殿顶周长是100米。
祈年殿殿顶的直径是多少米?
我根据C=πd推出d=C÷π,直接用推出的公式计算。
答:祈年殿殿顶的直径约是31.85米。
100÷3.14 ≈31.85(米)
圆的周长的一半
圆的直径
圆的周长的一半
半圆的周长不仅包括圆周长的一半,还包括直径的长度。
火眼金睛辨对错。
1
(1)圆周率就是3.14。 ( )
圆周率是一个无限不循环小数,在实际应用中,一般取它的近似值3.14。
×
(2)半圆的周长就是圆周长的一半。 ( )
×
3.14×(12×2)
=3.14×24
=75.36(厘米)
3.14×(18×2)
=3.14×36
=113.04(厘米)
答:时针走一圈,它的尖端走过的路程是75.36厘米。
分针走一小时,它的尖端走过的路程是113.04厘米。
(教材第63页“自主练习”第3题 )
2
时针
走一圈
走1小时
分针
长12厘米,如果 ,它的尖端走过的路程是多少? 长 18 厘米,如果 ,它的尖端走过的路程是多少厘米?
圆的半径(r)
圆的直径(d)
圆的周长(C)
2
9
18.84
4
12.56
4.5
28.26
6
3
(教材第63页“自主练习”第4题 )
请将表格补充完整。(单位:米)
3
(1) 3.14×5÷2
=15.7÷2
=7.85(米)
答:需要7.85米篱笆。
(2) 3.14×(5+2)÷2
=21.98÷2
10.99-7.85=3.14(米)
答:需要增加3.14米篱笆。
(教材第64页“自主练习”第8题 )
如图,依墙而建的鸡舍围成半圆形,其直径为
5米。
(1)需要多长的篱笆?
(2)如果将鸡舍的直径增加2米,
需要增加多长的篱笆?
4
=10.99(米)
1.57×40÷3.14÷2
=62.8÷3.14÷2
=20÷2
答:这个水池的半径是10米。
=10(米)
间隔
(教材第64页“自主练习”第10题 )
圆形水池四周种了40棵树,每两棵树之间的距离是1.57米,这个水池的半径是多少米?
4
以8棵树为例画示意图分析:
从图中可以看出,树的棵数=间隔数。
正确解答
围成圆的曲线的长度就是圆一周的长度,即圆的周长。
我明确了圆周长的意义。
同学们,这节课你们学会了哪些知识?
圆的周长= 圆周率×直径 C= πd
圆的周长= 圆周率×半径×2 C= 2πr
圆的直径= 圆的周长÷圆周率 d=C÷π
圆的半径=圆的周长÷圆周率÷2 r=C÷π÷2
我知道了圆周长的计算公式和推导公式。
同学们,这节课你们学会了哪些知识?
相关练习。
02
01
自主练习第1、2、5、6题。
